一种与N-Back诱发脑力疲劳相关的特异性脑电网络结构
2017-06-01孟桂芳许敏鹏张春翠綦宏志
孟桂芳 许敏鹏 张春翠 何 峰 綦宏志 明 东
(天津大学精密仪器与光电子工程学院生物医学工程系,天津 300072)
一种与N-Back诱发脑力疲劳相关的特异性脑电网络结构
孟桂芳 许敏鹏†张春翠 何 峰#*綦宏志*明 东
(天津大学精密仪器与光电子工程学院生物医学工程系,天津 300072)
探究脑力疲劳引起的静息态脑电网络结构的改变,以及体力疲劳的引入对脑力疲劳相关脑电网络的影响。分别以2-back实验和功率自行车诱发脑力、体力疲劳,采集10名被试脑力疲劳前后以及体脑疲劳前后4种状态下20个导联的静息脑电信号(EEG),进行偏定向相干因果性分析。对被试的脑电网络连接逐个进行威尔科克森符号秩检验,选择PDC值显著性大于阈值的连接赋为1,构建出二值化脑电网络。通过对疲劳前后脑电网络的比较与拆分计算,提取出一个N-back实验下与脑力疲劳相关的特异性脑电网络结构,该网络以额区的FP2导联为中枢节点,呈现出由全脑所有导联指向FP2的规律。在脑力疲劳和体脑疲劳两种疲劳状态下,该网络的连接形式基本保持一致,连接系数分别是4.060 3和4.142 1,没有发生显著改变,所以是一种相对独立、稳定并与脑力疲劳密切相关的功能网络。该方法和结果有望为研究脑力疲劳和探索体脑疲劳交互影响机制提供一个新的视角。
脑电网络结构;脑力疲劳;体脑疲劳;静息态;偏定向相干
引言
疲劳是由于长时间的体力活动或脑力负荷所引起的一种身心疲惫的状态,是日常生活中普遍存在的一种现象。Grandjean于1979年首次提出了脑力疲劳的概念,并且把疲劳划分为体力疲劳和脑力疲劳[1]。脑力疲劳在主观上表现为一种倦怠感,伴随有注意力不集中、心情烦闷等负性情绪,客观上会造成人的工作积极性降低、作业能力和作业绩效下降[2]。长期处于疲劳状态,还会导致焦虑症、抑郁症等各种慢性疾病。
在目前关于脑力疲劳的研究中,常见的疲劳评价指标包括疲劳量表、行为学参数、生理参数等。疲劳量表指导被试评价操作任务时的感受,较为主观。行为学参数用来衡量作业绩效的变化,如反应时间[2]、正确率[3]等,但不具备实时性。生理参数法应用极为广泛,通过提取人在作业过程中对疲劳敏感的生理参数实现疲劳状态的检测,具有实时、无创、敏感性强等优点。常用的生理信号包括心电[4]、眼电[5]、脑电和脑血氧饱和度[3,6]等。尤其是脑电信号,由于其时间分辨率高、功能特异性强等优势,被广泛应用于疲劳研究。Tran等采集模拟驾驶任务中的 EEG 信号,经多元方差分析发现,清醒和疲劳状态下的 α 波有显著差异,特别是Cz和P4导联,在疲劳状态下α 波明显增强[7];Kathner等采用字符拼写和双耳差听任务结合的方法诱发脑力疲劳,并分析了ERP信号,结果显示,随着疲劳的加深,PZ导联P300幅值下降[8]。但是,大脑不同的区域具有不同的功能,多个脑区相互协调完成人体各项生理活动[9],而以上所述的各种方法无法揭示疲劳前后大脑各个区域之间的信息传递与交流,因此从网络方面研究是非常有必要的。
在脑网络研究领域,复杂脑网络研究也被称为基于图论分析的脑网络研究[10]。图论是目前复杂网络分析领域最主要的数学工具[11],可以将一个复杂网络抽象为一个由节点集和边集组成的图,边表征其连接的两个节点间存在某种关系。构建基于多通道EEG信号脑网络,通常选取各导联电极覆盖的区域为一个节点,通过特定算法量化各导联信号之间的关系,进而构建出脑电网络。目前,量化两个导联信号之间关系的方法有很多种,如互相关、相位同步、互信息量等[12-13]。以上方法建立的网络是一种无向连接,无法反映两个节点间的因果关系,而因果分析方法建立的因效性连接可以描述节点间的信息传递[14]。最重要的一个因果分析思想,是由Cliver Granger提出的格兰杰因果性(Granger causality, GC)思想[15]。
偏定向相干(partial directed coherence,PDC)是在格兰杰因果性的基础上发展而来的一种频域因果分析方法,它通过对多路信号建立多变量自回归模型,再将模型参数变换到频域,得到不同导联信号之间的因果关系,进而有效估计各个信号之间的效应连接。PDC可直接计算各个通道脑电信号之间的相互作用关系,因此适用于多导联脑电网络的分析。基于此,本研究构建了两组实验疲劳前后静息态脑电网络图并对其进行分析,探索脑力疲劳所引起的网络结构的改变,以及体力疲劳的引入对于脑力疲劳相关脑电网络的影响。
1 方法
实验采集了10 名健康被试(7 名女生,3 名男生,(22±2) 岁)的脑电数据。所有被试均身体健康,无任何病史,无慢性疲劳症状,无运动障碍。被试在实验前3天没有过剧烈运动。
1.1 实验设计
1.1.1 脑力疲劳诱发实验
N-back是一种持续加工的任务类型,也是一种常用的脑力疲劳诱发方法。研究证明,30 min的2-back任务就可以诱发出脑力疲劳[16]。在本实验中,脑力疲劳采用字符2-back任务进行诱发,要求被试根据自己的记忆将当前出现的刺激字符与倒数第2个字符比较,并做出相应的反应:若相同为靶刺激,需按←键反应;若不同则为非靶刺激,按→键反应。26 个大写英文字母随机出现在屏幕中央,每个字符的呈现时间为0.5 s,两个字符之间间隔3 s,图1即为刺激字符呈现界面。

图1 2-back任务字符呈现界面Fig.1 Character interface of the 2-back task
1.1.2 体力疲劳诱发实验
在本实验中,体力疲劳诱发选择的是图2所示的优沃B300功率自行车,功率范围为0~300 W。

图2 功率自行车(优沃B300)Fig.2 Braked cycle ergometer (Smart B300)
在正式实验之前,要测量每名被试骑自行车的最大功率。首先被试以30 W的功率热身2 min,然后以10 W/min的速率增加,直到自行车转数小于60 r/min,记录此时的功率即为最大功率。在实验时,选取最大功率的40%来诱发体力疲劳。
1.1.3 实验流程
实验前向被试介绍实验流程,测量被试的最大功率,并练习字符2-back任务,随后进入正式实验。实验分为体脑疲劳诱发和单纯脑力疲劳诱发两组。体脑疲劳诱发方法为:被试执行字符2-back任务,同时以40%的最大功率骑自行车;脑力疲劳诱发方法为:被试执行字符2-back任务,同时以0W功率骑自行车。两组实验的流程相同,如图3所示:首先采集2 min的静息脑电数据,然后分别执行3次疲劳诱发任务,每次20 min,最后再次采集2 min静息脑电信号。每名被试进行2次实验,实验顺序随机,两次实验间隔3天,保证被试的体力得到充分恢复。

图3 实验流程Fig.3 Flowchart of the experiment
1.2 数据分析
在本研究中,使用的脑电采集设备是Neuroscan公司生产的32导联脑电放大器,采集软件为scan4.5系统。电极位置按照国际10-20标准安放,选择右耳乳突作为参考电极,采样频率1 000 Hz。
1.2.1 预处理
在采集信号时,由于某些因素的干扰,采集到的原始脑电信号往往含有噪声,因此要对其进行预处理,去除各种噪声和伪迹。本研究中的预处理包括:变参考至左右乳突、降采样至500 Hz,以及0.5~50 Hz带通滤波等。
1.2.2 偏定向相干
偏定向相干(PDC)是一种基于多变量自回归处理时间序列模型的格兰杰因果性频域测量方法。PDC是一个归一化的值,在[0,1]之间。PDCj→i表示从导联j流向导联i的信息占所有从导联i流出的信息的比值,值越大表明这两个通道的连接性越强。具体算法如下:
预处理后的脑电信号表示为一个矩阵,有
Y(n)=[y1(n),…,yM(n)]T
(1)
式中,M代表导联数。
Y(n)可用一个p阶AR模型表示为
(2)
式中,Ar是计算出的系数矩阵,E(n)是噪声。
将系数矩阵进行傅里叶变换,即
式中,I是一个M维单位矩阵。
这样,从导联j到导联i的PDC值可定义为
(5)
选取20个导联的脑电数据分析(M=20),将120 s的脑电数据每10 s计算PDC值,得到12个20×20的矩阵,叠加平均作为某一被试在特定静息状态下的连接矩阵。
1.2.3 基于图论的脑电网络构建
图论是用数学手段表示复杂网络并且可用图形呈现出来的一种有效方法。网络图包含节点和边这两个最基本的元素,可以用它的连接矩阵A来表示,矩阵元素aij代表节点i和j之间的连接性。
以20 个导联为节点、 PDC计算出的信息流强度(即PDC值)作为边、信息流方向作为边的指向,构建大脑皮层的有向加权脑电网络。其中,令每个导联与自身的PDC值等于0,即连接矩阵的对角线元素全部为0,以避免出现节点与自身连接(自连接)这种无意义现象。在加权网络中,定义与某节点相连的边的权重和为节点强度。
为直观分析疲劳前后的脑电网络结构变化,可以通过设定阈值对连接矩阵二值化,将加权脑电网络转化为二值网络进行分析。在二值网络中,aij=0表示节点i和j之间无连接,aij=1表示有连接。
具体做法见图4,对预处理后的20导联数据依次错位截取,计算得到12 个20×20的矩阵,求其平均作为该名被试在某种静息状态下的连接矩阵,再计算10名被试在4种静息状态下的380个有效连接(20个自连接赋值为0)的平均值作为本研究的阈值。基于该阈值,对所有被试的380个有效连接逐个进行秩检验,选择PDC值显著性大于阈值(P=0.01)的连接赋值为1,其余连接赋值为0,得到二值化的20×20矩阵。
[13]徐颖果:《跨文化视野下的美国华裔文学——赵健秀作品研究》,天津:南开大学出版社,2008年,第21页。

图4 矩阵二值化流程Fig.4 Flowchart of matrix binaryzation
以20 个导联为节点,以某种静息状态下二值化矩阵元素为边,即可构建该状态对应的有向二值网络。为了方便比较,可根据网络中枢节点将网络拆分成不同的子网络。
另外,定义某个网络的连接系数为该网络中各个中枢节点的节点强度之和,即网络中所有连接在原始加权网络矩阵中对应的PDC值之和。分别计算10名被试各状态下的连接系数及平均连接系数,利用配对t检验对结果进行统计分析。
2 结果
作业绩效可以从一定程度上反映被试者对于实验任务的参与程度,而作业绩效的变化则是被试者疲劳状态变化的客观描述。分别计算10名被试执行2-back任务时对于所有字符的平均反应正确率和靶刺激字符的平均反应正确率,结果如表1所示。
表1 2-back实验字符反应正确率
Tab.1 The operation accuracy and target accuracy of the subjects for the 2-back task

实验次数所有字符反应正确率/%靶刺激字符反应正确率/%脑力疲劳196.2±2.892.3±6.6295.7±3.390.2±8.3393.4±6.684.1±15.1体脑疲劳195.1±3.690.4±7.6294.0±4.286.8±10.5394.2±3.086.8±7.7
从表1中可以看出,在脑力疲劳实验中,随着疲劳诱发时间的延长,被试反应正确率逐次下降,并且对靶刺激反应正确率的下降更明显。这说明,随着疲劳诱发时间的增加,被试的认知能力逐渐下降,疲劳程度增加。总体来讲,被试的反应正确率在体脑疲劳实验中低于在脑疲劳实验中,这可能是由于体力任务分散了被试者的部分注意力。
在秩检验后,得到4种状态下有向二值脑电网络结构,如图5所示。
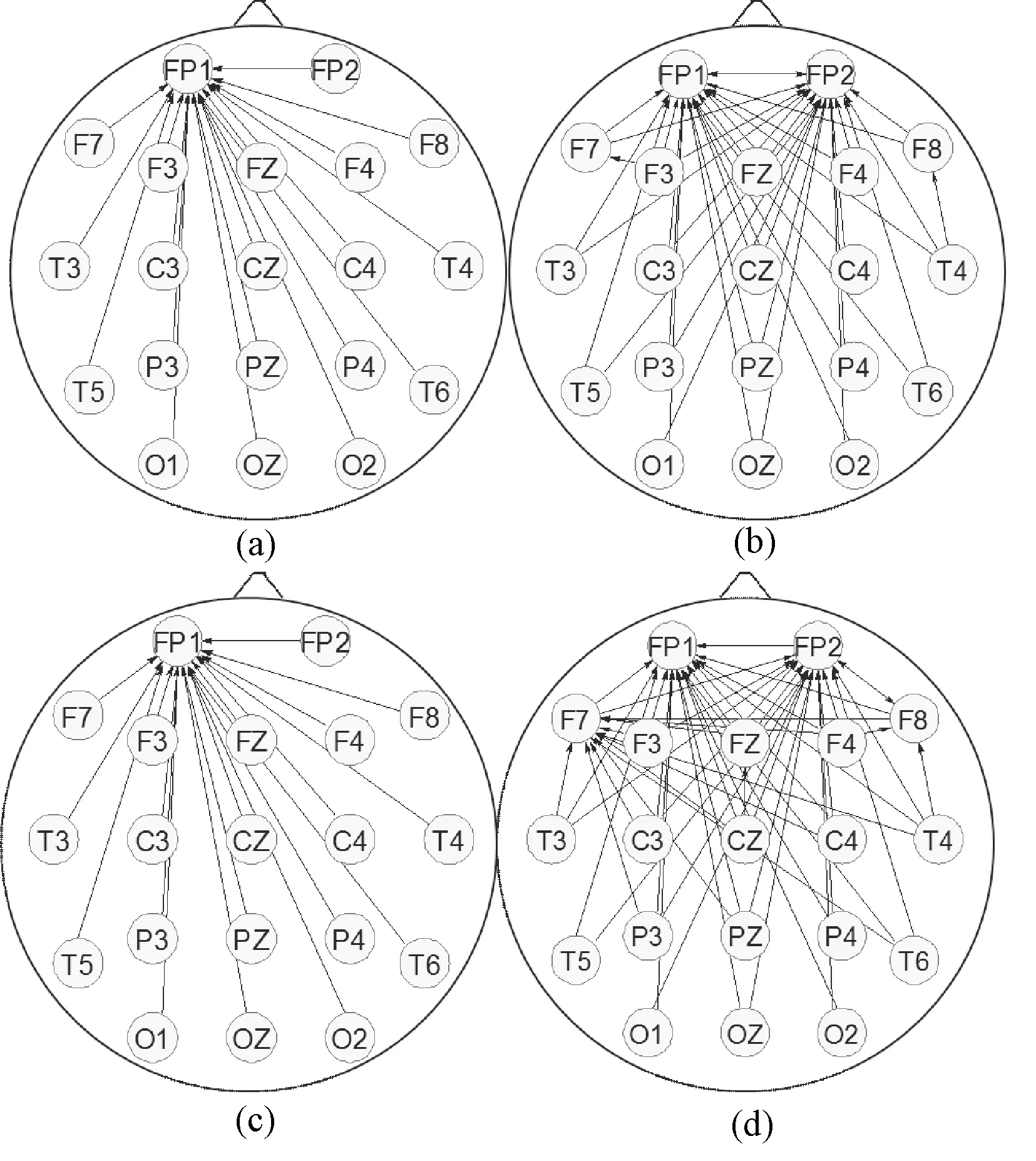
图5 不同状态下的静息脑电网络。(a)脑力疲劳前;(b)脑力疲劳后;(c)体脑疲劳前;(d)体脑疲劳后Fig.5 Resting EEG network in different state. (a)Before mental fatigue; (b)After mental fatigue; (c)Before physical-mental fatigue; (d)After physical-mental fatigue
从脑电网络可以直观看出,疲劳后网络的连接性比疲劳前的复杂。具体来讲,脑力疲劳和体脑疲劳前,信息流一致指向FP1导联;脑力疲劳后,FP2导联流入的信息增多;而体脑疲劳后,FP2和F7导联流入的信息增多。将图5(b)的脑力疲劳后脑电网络拆分成分别以中枢节点FP1、FP2为中心的不同子网络,如图6所示。
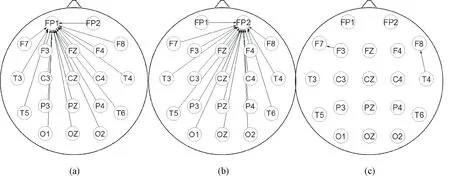
图6 脑力疲劳后静息脑电网络结构的子网络。(a)子网络1,非疲劳相关子网络;(b) 子网络2,脑力疲劳相关子网络;(c)残差子网络Fig.6 Subnetworks of resting EEG network structure after mental fatigue. (a) Subnet 1, non-fatigue-related subnetwork; (b) Subnet 2, mental fatigue-related subnetwork; (c) Residual subnetwork
为了进一步验证图6(b)是一个与脑力疲劳相关的网络,又对图5(d)所示的体脑疲劳后脑电网络进行拆分,以观察是否还存在与6(b)相同或相似的网络,结果如图7所示。
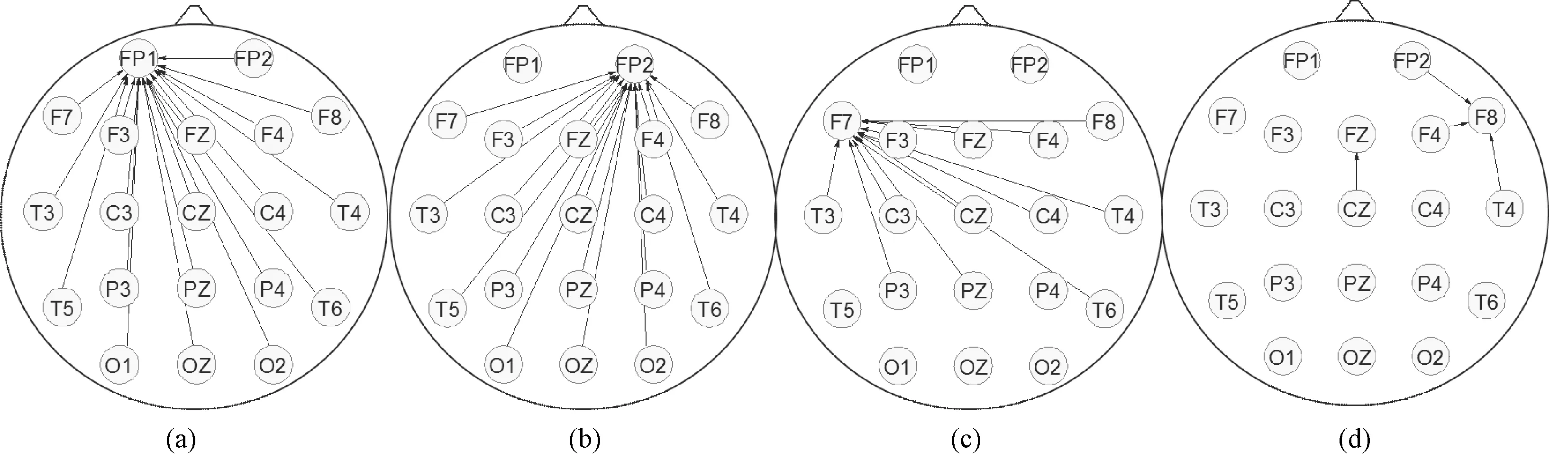
图7 体脑疲劳后静息脑电网络结构的子网络。(a) 子网络1,非疲劳相关子网络;(b) 子网络2,脑力疲劳相关子网络;(c) 子网络3,体力疲劳相关子网络;(d)残差子网络Fig.7 Subnetworks of resting EEG network structure after physical-mental fatigue. (a) Subnet 1, non-fatigue-related subnetwork; (b) Subnet 2, mental fatigue-related subnetwork; (c) Subnet 3, physical fatigue-related subnetwork; (d) Residual subnetwork
由图7(a)与图5(a)、(c)所见,疲劳前的网络结构完全相同;图7(b)与6(b)的结构基本是相同的,所以认为这是一个N-back实验条件下与脑力疲劳相关的子网络;较脑力疲劳实验而言,由于体脑疲劳实验中增加了体力疲劳诱发实验,出现了图7(c)中以F7为中枢节点的子网络,因此称之为体力疲劳相关子网络;图7(d)为残差子网络。
表2是4种静息态脑电网络及各子网络的连接系数。在脑力疲劳后,非疲劳相关子网络的连接系数(6.807 3)与疲劳前的连接系数(6.754 0)相比,基本没有变化(t自由度=9,P=0.95);在体脑疲劳后,脑力疲劳相关子网络的连接系数(4.060 3)与脑力疲劳后的连接系数(4.142 1)相比并没有发生显著改变(t自由度=9,P=0.79),而非疲劳相关子网络的连接系数(5.694 0)与疲劳前(6.791 9)相比则有所降低(t自由度=9,P=0.55)。
表2 疲劳前后子网络连接系数(平均值)
Tab.2 Average connection coefficient of sub-network before and after fatigue
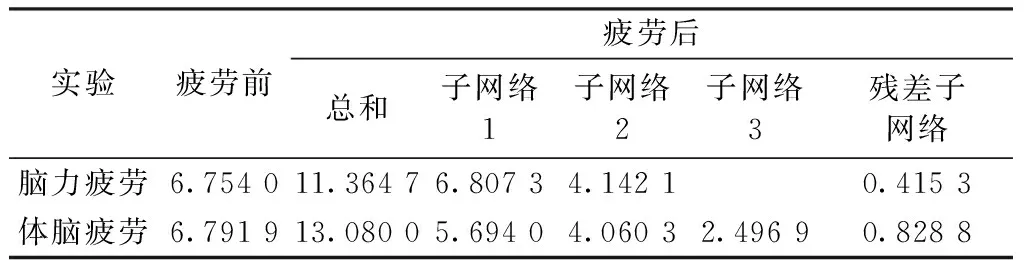
实验疲劳前疲劳后总和子网络1子网络2子网络3残差子网络脑力疲劳6.754011.36476.80734.14210.4153体脑疲劳6.791913.08005.69404.06032.49690.8288
3 讨论
目前,在体脑疲劳交互影响的研究中,大多学者致力于观察脑力疲劳程度对于体力疲劳及其恢复的影响。Mehta等在被试执行体力疲劳诱发任务实验时加入脑力负荷任务,观察到额外脑力负荷会减小肌肉收缩力,缩短肌力持续时间,增加疲劳感觉,并且延长肌肉疲劳恢复时间,证明了脑力疲劳会严重影响体力疲劳及其恢复[17-18]。Shortz等研究了脑力疲劳对体力疲劳的影响,实验同样观察到脑力疲劳会导致体力运动可持续时间的下降和体力疲劳感觉的增加[3]。反之,关于体力疲劳对脑力疲劳影响的研究较少,而本研究恰好补充了相关内容,从脑电网络的角度揭示了体力疲劳的引入对于脑力疲劳状态下脑电网络结构的影响。结果表明,N-back实验诱发脑力疲劳后会形成一个相对独立的、稳定的网络结构,体力疲劳的引入并不会改变脑力疲劳相关脑电网络的结构,也不会造成该网络连接的增强或者减弱,但是会影响非疲劳相关子网络。
不同状态下的脑电网络结构显示(见图5),疲劳前的脑电网络结构比较简单,呈现出由全脑所有导联指向FP1的规律。脑力疲劳后的静息状态脑电网络可以拆分为非疲劳相关子网络和脑力疲劳相关子网络,见图6。其中,非疲劳相关子网络与疲劳前静息态脑电网络结构相同,以FP1导联为中枢节点;而脑力疲劳相关子网络以FP2导联为中枢节点,同样呈现出由全脑所有导联指向FP2的规律。与脑力疲劳相比,体脑疲劳后的脑电网络在其基础上增加了一个与体力疲劳密切相关的脑电子网络。体力疲劳相关子网络与前两个子网络有所不同,其网络连接主要是由顶区、中央区和额区的P3、PZ、P4、C3、CZ、C4、 F3、FZ、F4等导联指向侧额的F7导联。以上所述为疲劳前、后以及脑力疲劳和体脑疲劳间脑电网络结构上的差异,而网络连接系数则可以定量描述疲劳对于静息态脑电网络的影响,以及不同脑电网络之间的相互影响。
整体来看,无论是脑力疲劳实验还是体脑疲劳实验,网络连接系数,疲劳后(11.364 7,13.080 0)较疲劳前(6.754 0,6.791 9)均有显著增加(t自由度=9,P<0.001,P<0.001)。具体到子网络两组实验,则有所不同。脑力非疲劳相关子网络的连接系数,疲劳后(6.807 3)与疲劳前(6.754 0)相比,基本没有变化(t自由度=9,P=0.95);也就是说,在N-back实验任务下,脑力疲劳会形成一个相对独立的网络结构,而不会对原有的非疲劳态脑电网络产生影响,故称之为“脑力疲劳相关子网络”。脑力疲劳相关子网络的连接系数,体脑疲劳后(4.060 3)与脑力疲劳后(4.142 1)相比,并没有发生明显改变(t自由度=9,P=0.79);而非疲劳相关子网络的连接系数,疲劳后(5.694 0)与疲劳前(6. 791 9)相比,则有一定程度的降低(t自由度=9,P=0.55)。这意味着体力疲劳引入一个新的网络结构(称之为“体力疲劳相关子网络”),可能会影响非疲劳态脑电网络,使网络连接系数降低,但是并不会造成脑力疲劳相关子网络连接的增强或者减弱。
从信息流向来看,疲劳相关的脑电网络总体呈现为由大脑皮层后部指向额区,额区与记忆、情绪等高级认知功能紧密相关,是大脑进行信息加工处理的综合区域[19]。认知任务需要各个脑区的广泛参与和协作,所以在脑力疲劳相关的因果网络中,FP2是信息流的“果”,而信息流的“因”几乎包含了FP2以外所有的导联。顶区和中央区是与运动有关的脑区[20],所以在体力疲劳的相关子网络中,信息流的“因”集中在顶区和中央区的几个导联,而信息流的“果”则是在F7,这一点可以用Lorist等的一项研究[17]来解释。他们发现,在进行力的收缩任务时,大脑背外侧前额叶皮质会被明显激活,体脑疲劳的相互影响可能发生在脑区背侧的前额叶皮质,但是这种相互影响的机制还并不明确。
4 结论
本研究利用偏定向相干(PDC)方法,对脑力疲劳和体脑疲劳两组实验受试者的静息态EEG信号做了信息流因果分析,并构建了基于图论的脑电网络,通过疲劳前后网络结构变化的对比以及脑力疲劳和体脑疲劳间网络差异的分析,提取出一个与脑力疲劳相关的特异性脑电网络结构,而且证明该网络是相对独立的,不会受到体力疲劳的影响,为体脑疲劳交互影响机制的解释提供了一种新的思路。
[1] Grandjean E. Fatigue in industry [J]. Br J Ind Med, 1979, 36(3): 175-186.
[2] Faber LG, Maurits NM, Lorist MM. Mental fatigue affects visual selective attention [J]. PLoS ONE, 2012, 7(10): 48073- 48073.
[3] Shortz AE, Van DS, Mehta RK. Neural correlates of physical and mental fatigue [C] //Beringer DB, eds. Proceedings of the Human Factors and Ergonomics Society Annual Meeting. New York: Sage Publications, 2012, 56(1): 2172-2176.
[4] Zhao Chunlin, Zhao Min, Liu Jianpin, et al. Electroencephalogram and electrocardiograph assessment of mental fatigue in a driving simulator [J]. Accid Anal Prev, 2012, 45: 83-90.
[5] Chieh TC, Mustafa MM, Hussain A, et al. Development of vehicle driver drowsiness detection system using electrooculogram (EOG) [J]. Computers, Communications & Signal Processing with Special Track on Biomedical Engineering, 2005,1: 165-168.
[6] Muthalib M, Kan B, Nosaka K, et al. Oxygen Transport to Tissue XXXV [M]. New York:Springer, 2013: 73-79.
[7] St. John M, Kobus DA, Morrison JG, et al. Overview of the DARPA augmented cognition technical integration experiment [J]. International Journal of Human-Computer Interaction, 2004, 17(2): 131-149.
[8] Käthner I, Wriessnegger SC, Müller-Putz GR, et al. Effects of mental workload and fatigue on the P300, alpha and theta band power during operation of an ERP (P300) brain-computer interface [J]. Biological psychology, 2014, 102: 118-129.
[9] Buzsaki G. Rhythms of the Brain[M]. New York: Oxford University Press, 2006:52-53.
[10] 孙俊峰,洪祥飞,童善保. 复杂脑网络研究进展:结构、功能、计算与应用 [J]. 复杂系统与复杂性科学, 2011, 7(4): 74-90.
[11] 王春方,孙长城,张希,等. 基于偏定向相干性(PDC)的脑卒中后抑郁症患者脑网络研究 [J]. 中国生物医学工程学报, 2015, 34(4): 385-391.
[12] Hurtado JM, Rubchinsky LL, Sigvardt KA. Statistical method for detection of phase-locking episodes in neural oscillations [J]. Journal of Neurophysiology, 2004, 91(4): 1883-1898.
[13] Sun J, Small M. Unified framework for detecting phase synchronization in coupled time series [J]. Physical Review E, 2009, 80(4): 046219-046219.
[14] 黄亮,吴超华,高小榕. 基于自回归模型和相位斜率指数的动态脑连接分析 [J]. 中国生物医学工程学报, 2016, 35(1): 1-9.
[15] Granger CWJ. Investigating causal relations by econometric models and cross-spectral methods [J]. Econometrica, 1969, 37(3): 424-438.
[16] Tanaka M, Mizuno K, Tajima S, et al. Central nervous system fatigue alters autonomic nerve activity [J]. Life Sciences, 2009, 84(7): 235-239.
[17] Lorist MM, Kernell D, Meijman TF, et al. Motor fatigue and cognitive task performance in humans [J]. The Journal of physiology, 2002, 545(1): 313-319.
[18] Mehta RK, Agnew MJ. Effects of concurrent physical and mental demands for a short duration static task [J]. Int J Ind Ergonom, 2011, 41:488-493.
[19] Ridderinkhof KR, Ullsperger M, Crone EA, et al. The role of the medial frontal cortex in cognitive control [J]. Science, 2004, 306(5695): 443-447.
[20] Gao Qing, Duan Xujun, Chen Huafu. Evaluation of effective connectivity of motor areas during motor imagery and execution using conditional Granger causality [J]. Neuroimage, 2011, 54(2): 1280-1288.
A Specific EEG Network Structure Related to Mental Fatigue Induced by N-back
Meng Guifang Xu Minpeng†Zhang Chuncui He Feng#*Qi Hongzhi*Ming Dong
(Department of Biomedical Engineering,College of Precision Instrument and Opto-Electronics Engineering,Tianjin University,Tianjin 300072,China)
The aim of this study was to investigate the changes of resting state EEG network structure caused by mental fatigue, and the influence of physical fatigue on the mental fatigue-related EEG network. Two-back task and cycling were used to induce mental fatigue and physical fatigue, respectively. Twenty channels of resting state EEG of 10 subjects were collected under 4 different fatigue conditions. EEG networks were obtained by calculating the partial directed coherence (PDC) causality between two arbitrary nodes and refined by comparing to a threshold. Only those links significantly higher than the threshold would be reserved, while others dismissed. After a comparison among the four EEG networks, a mental fatigue-related specific EEG network structure in N-back experiments was identified, in which FP2 was the hub while almost other channels had a link with it. The network structure was very stable, and its corresponding linking strength 4.0603 and 4.1421 in two fatigue state, which would not be influenced by physical fatigue. Therefore, this study identified an independent and stable functional network related to mental fatigue. The result provided a new perspective on the neural mechanism of mental fatigue and the relationship between mental fatigue and physical fatigue.
EEG network structure; mental fatigue; physical-mental fatigue; resting state; partial directed coherence(PDC)
10.3969/j.issn.0258-8021. 2017. 02.003
2016-05-30, 录用日期:2016-10-13
国家自然科学基金重大研究计划(91520205);国家自然科学基金(81571762);国家自然科学基金(31500865)
R318
A
0258-8021(2017) 02-0143-07
†共同第一作者(Co-first author)
# 中国生物医学工程学会高级会员(Senior member, Chinese Society of Biomedical Engineering)
*通信作者(Corresponding author),E-mail: heaven@tju.edu.cn,qhz@tju.edu.cn
