基于ABAQUS的板材精冲工艺研究
2017-05-31鲁子恒雷君相
鲁子恒+雷君相


摘要:
构建厚度为1.5 mm的板材精密冲裁有限元模型,分析板材精冲的变形过程.通过大量有限元模拟,重点分析压边力和反压力对精冲断面质量的影响规律,并将模拟结果和试验结果进行对比分析.结果表明:当压边力不变时,随着反压力的增大,精冲断裂带长度不断减小,而断面平整度逐渐变差;当反压力不变时,断裂带长度不随压边力的增大发生较大改变,但断面平整度提高;当压边力和反压力相互配合时,冲孔断裂带最小,断面平整度最好;模拟结果与试验结果非常接近,说明压边力对精冲断面质量影响规律的模拟结果准确.
关键词:
板材精冲; 有限元模拟; 反压力; 压边力
中图分类号: TG 386-文献标志码: A
Research on Fine-blanking Technology Based on ABAQUS
LU Ziheng, LEI Junxiang
(School of Materials Science and Engineering, University of Shanghai
for Science and Technology, Shanghai 200093, China)
Abstract:
This paper presents building a finite element model of the fine blanking with a thickness of 1.5 mm plate and studying the plate deformation process by fine blanking.The effect on fracture surface by fine blanking through blank holder force and back pressure was analyzed.Both of simulations and experimental results similarly indicated that:when blank holder force was kept constant,the increase of back pressure shows fault zone was decreased and smooth finish got worse by fine blanking; when back pressure was kept constant,the increase of blank holder force manifests fault zone was not changed a lot but smooth finish got better; there is optimal point by using both to minimize the fault zone and obtain best smooth finish.
Keywords:
plate fine-blanking; finite element simulation; back pressure; blank holder force
精密冲裁简称精冲.精冲是在普通冲压技术基础之上发展起来的,具有优质、高效、低耗和面广等特点.随着科学技术的飞速发展,对零件的质量要求也越来越高,普通冲孔的精密程度已经无法满足需求.经过许多学者的长期研究,精密冲孔技术应运而生,它优化了金属板料的加工工艺链.LEE等[1-2]对精冲过程进行了有限元模拟,开发了相关的网格重画程序;彭群等[3]通过有限元模拟,预设损伤破坏临界值,预测了裂纹的产生;HATANAKA等[4-6]对冲裁裂纹的衍生和扩展进行了分析讨论,分析了各工艺参数对冲裁断面质量的影响,有限元模拟结果与试验结果一致;CHAN等[7-8]用ABAQUS对整个精冲过程进行有限元模拟,分析得出了变形区的应力应变分布规律;HAMBLI等[9-10]对冲裁断裂准则进行了深入广泛的试验和分析研究.
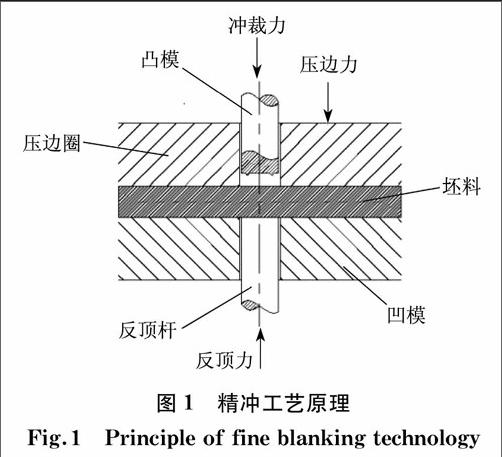
精冲过程中,凸模接触坯料之前,压边圈压紧板料,在压边圈与凹模之间产生竖向压应力,并且在坯料断裂过程中,由于挤压作用产生横向弹性变形,而产生横向压应力.在凸模压入坯料的同时,反顶杆对坯料施加反压力,反顶杆与凸模相互作用产生豎向压应力,凸模上的V形齿圈压入坯料时产生横向压应力,阻止了金属材料在剪切过程中的撕裂和横向流动,坯料在压紧状态下由冲裁力作用,凸模沿着凹模刃口的形状以纯剪切的形式对坯料冲孔.
为了防止冲孔得到的带孔板料表面出现压痕,V型齿圈被建立在凸模上.本文通过对SUS304不锈钢箔材在不同反压力、压边力作用下的精冲过程进行有限元模拟分析,研究了压边力、反顶力对精冲质量的影响规律,并与试验结果进行对比来分析模拟结果的准确性.
1 有限元模拟
1.1 精冲模型的建立
运用ABAQUS6.14模拟整个精冲过程.在建模过程中选择二维轴对称模型,这样能减少单元数,缩短计算时间,而且还能在保证同样多网格数的前提下,细化坯料剪切带的网格,使模拟结果更接近实际.精冲工艺原理见图1.
精冲模拟过程所选用的零件材料为SUS304不锈钢箔材.不锈钢箔材厚度为1.5 mm.建模时,将箔材设置为弹塑性体,模具设置为刚性体.模型的网格划分如图2所示,网格数为1 389.为保证模型计算精度,在凸凹模剪切带采取四边形单元,细化网格,因为板料在精冲过程中剪切带网格变形严重,如果不细化,可能导致模拟结果不准确,甚至可能因为网格畸变过大而报错,达不到计算的目的.
根据通用技术标准,可以确定精冲各参数范围值.表1为精冲有限元模拟的基本工艺参数,在模拟过程中不考虑温度对精冲过程的影响.其中RP、Rd分别为凸凹模的圆角半径.在模拟过程中,凸模与板料之间的接触关系为切向摩擦,将摩擦因数设置为0.125.
1.2 精冲过程凸模的载荷分析
图3为精冲模拟过程中凸模载荷—位移曲线.此次模拟过程中,凸凹模间隙为0.05 mm,压边力为1 700 N,反顶力为500 N.由图3可知,凸模向下运动接触材料后,V形齿圈压入坯料中,此时曲线斜率较小,完成第1个分析步.材料经过短暂的弹性变形转变成塑性变形,此过程中,凸模所受到的载荷随位移逐渐增大.随着凸模进一步下压,剪切厚度逐渐减小,但是由于材料在剪切过程中存在硬化作用,凸模载荷会继续增大.当凸模位移到达0.67 mm时,载荷达到最大值4 604 N.隨着凸模继续下压,剪切厚度进一步减小,凸模载荷随位移缓慢减小直到最后完成整个冲裁过程.凸模最大载荷一般出现在冲裁过程的1/5~1/3处.由图3可知,凸模载荷最大时,位移为0.67 mm,正处于此范围内.根据剪切力的计算公式:
F=L×S×σb×f
式中:L为剪切线长度;S为板料厚度;σb为材料抗拉强度;f为系数,通常取0.9.
将L=2π mm,S=1.5 mm,σb=520 MPa,f=0.9,代入式(1)得F=4 409 N.
图3所示模拟结果最大载荷为4 604 N,与经验公式计算出的剪切力相差4.4%,说明模拟结果精确.
2 模拟结果分析
2.1 反压力对精冲质量的影响
在精冲的过程中,反压力是精冲工艺参数中非
常重要的参数之一.它作用于呈平面的反顶杆上,反压力与压边力协同作用,不但可以使精冲变形区产生三向压应力,并且抑制坯料在加工过程中发生弯曲.反压力太小时,会使得材料在变形区的三向应力不足,使得坯料在精冲后成形质量不好;反压力太大,会增加冲裁力,也增加了模具的载荷,因此需要通过模拟分析选择出最合适的反压力.
反压力分别取100,500,800和1 000 N进行有限元模拟.图4所示为不同反压力下,精冲行程为0.5 mm时的静水应力分布图.
由图4可以看出,随着反压力的增加,反压板、坯料和凹模间产生的空腔体积不断减小.这是由于反压力的增加,使得坯料在变形区受到的压力增加,使得反压板跟坯料在冲孔过程中连接得更紧密.从图4(a)中可以看出,在此行程下,当反压力为100 N时,此时静水应力约为287 MPa.但是已经产生空腔,这是由于反压力过小,冲孔过程中拉应力增加, 压应力减小,导致坯料在冲孔过程中发生弯曲变形,使得坯料断裂时不能发生纯剪切断裂.在冲孔过程中,应该避免产生空腔,材料不发生弯曲变形.发生弯曲变形会使得坯料塑性变形时间缩短,过早发生断裂,影响孔的成形质量.当反压力为500 N时,空腔体积依然没有变小,这个时候断裂区静水应力约为830 MPa;当反压力为800 N时,已经不存在空腔,静水应力为979 MPa左右;当反压力增加到1 000 N时,静水应力约为1 007 MPa.可以看出,从500 N增加到1 000 N时,静水压力不断增加,这说明反压力可以明显地提高精冲过程中变形区的静水压力.
压边力取2 000 N,反压力分别取100,500,800和1 000 N进行有限元模拟.模拟结果如图5所示.
随着反压力的提高,断裂带不断减小.当反压力为100 N时,坯料断裂面的光滑带占整个断面的77%,断裂带长度为0.35 mm;当反压力达到500 N时,断裂带长度有了略微减少,使得断裂面光滑带达到整个断面的78%,断裂带长度为0.33 mm;当反压力为800 N时,断裂带长度为0.21 mm,断裂带的长度明显减小,断裂带的比例由22%降为14%.可以看到当反压力增加到800 N时,坯料的塑性明显变好,使得断裂带长度明显降低,但是坯料的断面上有部分不平整;当反压力到1 000 N时,已经完全消除断裂带,冲头行程达到0.18 mm时才发生完全断裂,冲头的行程已经超过坯料厚度时才发生完全断裂,但是断面上损伤的部分略多,导致断面不平整.在压边力为一定值时,当反压力逐渐增加时,断裂带的长度逐渐减小,反压力达到1 000 N时,可以完全消除断裂带.但是在一定的压边力下,反压力越大时,断面平整度不但没有提高,反而随着反压力的增加而降低.
2.2 压边力对精冲质量的影响
反压力取800 N,压边力分别取1 000,1 300,1 700和2 000 N进行模拟,模拟结果如图6所示.
从图6中可以看出,在精冲过程中,反压力不变,压边力越大坯料断裂区受到的静水压力越大,断裂带的长度逐渐减小.当压边力增大到1 700 N之后,断裂带的长度基本保持不变,但是断裂面的平整度得到提高.除了断裂带,断面其他部分基本上没有损伤,得到非常好的精冲质量.
通过分析反压力和压边力对精冲质量影响的模拟结果,可以分别得到这两个参数对精冲质量的影响规律:当压边力一定时,反压力对提高材料的塑性变形性能有非常大的影响;当反压力一定时,压边力对材料的塑性变形性能的影响程度有限,但是对材料的断裂面的平整度影响很大.反压力和压边力都是影响精冲质量的决定性因素,只有两者相互配合才能冲裁出断裂带最小、光滑带平整的高质量断面.
因此,取不同的反压力和压边力来模拟分析.结果表明:反压力为1 000 N、压边力为2 000 N时,精冲效果最好.如图6所示,断裂带长度约为0.1 mm,断裂面粗糙度达到了93%.观察图6可以推断,断裂带产生的主要原因在于凸凹模间隙.间隙的存在使得坯料存在无法处于三向应力作用下的空白区域,由于此处拉应力过大而产生的断裂带.当继续增加反压力和压边力时,坯料的精冲质量并没有得到提高,反而有所下降.所以反压力为1 000 N、压边力为2 000 N时,为最合理的精冲模拟工艺参数.
3 分析与讨论
为了分析反压力对精冲质量的影响规律,试验采用SEM对精冲孔断面进行分析,断面质量如图7所示.可以看出,随着反压力的增大,光滑带高度显著增加,断裂带高度明显减小.同时当反压力达到1 000 N时,部分断面已经完全消除了断裂带,但是断面损伤比较严重,影响断面质量.因此,在进行微孔冲裁时最佳冲裁反压力在800 N左右,所获得冲孔断面的质量较好.
对比试验结果与模拟结果如图9所示.光滑带尺寸随着反压力的增大表现出相同的变化规律,证明了模拟的合理性.模拟值比试验值偏大,这是因为在用ABAQUS建模时接触条件的设定与断裂参数的选择与真实冲裁过程有一定偏差.
图10(a)、图10(b)分别为数值模拟和扫描电子显微镜下拍摄的试验冲裁断面图,模拟断面光滑带高度为1.4 mm,占总断面高度的93%;试验结果中,光滑带高度为1.35 mm,占总断面高度的90%,两者结果非常接近.從两组数据可知,第2节中压边力对精冲断面质量的影响规律的模拟结果准确:压边力对材料的塑性变形性能的影响程度有限,但是对材料的断裂面的粗糙度影响很大.
4 结 论
(1) 精冲过程中压边力保持不变,随着反压力的增加,材料变形区受到的三向应力逐渐增大,延缓了坯料的裂纹产生的时间,断裂带的长度逐渐变小.当反压力达到一定值时,精冲质量己经有了很好的改善.继续增加反压力,虽然延缓了坯料发生断裂的时间,但是断面光洁度并没有提高,甚至变得更低,反而影响了精冲质量.
(2) 反压力保持不变,压边力越大,断裂带的长度逐渐减小,材料的塑性变形性能越来越好;当压边力达到一定值时,随着压边力的增加,断裂带的长度基本保持不变,但是断裂面的粗糙度逐渐提高.
(3) 反压力对于延缓坯料的断裂起着关键作用,压边力对于坯料的断面平整度起着关键作用.两者相互配合,冲孔断面断裂带小、粗糙度高,精冲效果达到最好.
参考文献:
[1] LEE T C,CHAN L C,WU B J.Further investigation of the fine-blanking process employing large deformation theory[J].Journal of Materials Processing Technology,1997,66(1/3):258-263.
[2] KUGLIN C D,HINES D C.The phase correlation image alignment method[C]∥Proceedings of the 1975 IEEE International Conference on Cybernetics and Society.San Francisco,CA,USA:IEEE,1975:163-165.
[3] 彭群,赵彦启,李荣洪,等.强力压边精冲技术的数值模拟[J].锻压技术,2004(4):23-25.
[4] HATANAKA N,YAMAGUCHI K,TAKAKURA N.Finite element simulation of the shearing mechanism in the blanking of sheet metal[J].Journal of Materials Processing Technology,2003,139(1/3):64-70.
[5] OZAKI T,YOSHIKAI T.On the mechanism of punching processing of small holes[J].Journal of Materials Processing Technology,1972(140):683-688.
[6] GAO Y,ZHOU N,YANG F,et al.P-phase precipitation and its effect on martensitic transformation in (Ni,Pt)Ti shape memory alloys[J].Acta Materialia,2012,60(4):1514-1527.
[7] CHAN L C,LEUNG Y C,LEE T C,et al.Numerical simulation for fine-blanking-a new approach[J].Materials Science and Engineering:A,2004,364(1/2):207-215.
[8] JEONG S,KANG J,OH S.A study on shearing mechanism by FEM simulation[C]∥Proceedings of the fifth international conference on technology of plasticity.Columbus,Ohio,USA,2006:631-634.
[9] HAMBLI R,RESZKA M.Fracture criteria identification using an inverse technique method and Blanking experiment[J].International Journal of Mechanical Sciences,2002,44(7):1349-1361.
[10] HAMBLI R.Comparison between Lemaitre and Gurson damage models in crack growth simulation during blanking process[J].International Journal of Mechanical Sciences,2001,43(12):2769-2790.
