矿区公路中投影长度变形的分析处理

刘 舜，田正华

(陕西铁路工程职业技术学院，陕西 渭南 714000)

矿区公路中投影长度变形的分析处理

刘 舜，田正华

(陕西铁路工程职业技术学院，陕西 渭南 714000)

由于投影面选择问题，矿区公路平面控制网建立中存在投影变形现象。规范规定，公路测区内投影长度变形值不得大于2.5 cm/km。分析提出，通过修改全站仪格网因子抵消高程改化从而减小投影长度变形值的方法，具有一定的实际意义。

平面控制测量；高程改化；投影变形；格网因子

一般矿区地形复杂，覆盖面积大，会出现在复杂地形间修建公路的情况，这就必须要建立统一、系统的工程控制网以适应公路建设的需要。但是这样就会造成两个基准面(坐标系统投影面以及施工高程面)之间的不统一，从而使得投影长度变形值超过限差(2.5 cm/km)要求，如果不进行投影改正，会对施工产生不良的影响[1-2]。

1 工程案例

以某矿区公路的施工测量工作为例，该工程位于重庆境内，地形复杂、群山绵延，部分孤峰独起，其间沟谷相对平坦开阔，呈舒缓波状。地势总体呈西高东低，地面高程一般在850～1 000 m之间。

使用尼康350和索佳250R全站仪分别对二工区驻地附近的控制点k503和k504进行对向观测，测得平距为547.728 m，依据设计院提供的坐标进行反算的平距为547.651 m，这两者相差7.7 cm，超过了投影长度变形2.5 cm/km的限差要求，因此会对施工放样产生一定影响。据技术员反映，这一现象普遍存在，且距离越大差值越大。部分基线边边长数据如表1所示。

表1 部分基线坐标推算数据与全站仪实测数据对比表

2 投影变形分析

用华测GPS接收机对k503和k504基线进行两个时段的观测，每个时段1 h。因为k503和k504的标高大小在900 m左右，所以对基线进行解算时，分别向大地高为0 m和900 m的投影面进行投影，解算平距分别为547.654 0和547.730 1 m。通过数据可以发现：基线投影到0 m投影面时距离接近于设计院提供的GPS测量平距，基线投影到900 m投影面时距离接近于全站仪实测距离。

可得出结论：设计院在进行GPS测量时，提供的为1.5(°)分带，投影至参考椭球面的坐标系，这就造成在本地区的施工高程面与统一坐标系的投影面分离，造成实测两点距离与坐标推算距离相差超过2.5 cm/km的限差。这也是工程建设中常见的坐标系统投影面和施工高程面不一致的问题[3]。

在控制测量计算中，有两项投影计算会引起长度变形：a地面观测值投影到参考椭球面，控制测量中需要投影到某一高程为H0的水平基准面，称为边长的高程投影；b参考椭球面边长投影到高斯平面，也会导致边长的变形，称为高斯投影。

1) 地面观测值归算至椭球面的长度变形

使用全站仪观测得到的是地面上两点的直线斜距，即图1中所示的S，将其归算到椭球面上的距离，由图中可以看出两者之间产生一个变形量△S1，可由下式计算得到：

图1 地面观测值归算至参考

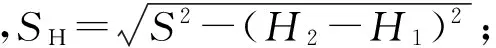
RA——测线方向的椭球曲率半径。

H=(H1+H2)/2，H1和H2分别代表A、B两点(测距光线两端)的大地高，大地高可通过下式计算：

Hi=H正常+δ+i

其中δ——所在测区高程异常值；

i——测站高度；

H0——任意高程面，H0=0时即为投影至参考椭球面。

表2列出了在不同高程面上依据投影变形公式计算的每千米长度投影变形值和相对变形值。这里RA取近似值为6 370 km。

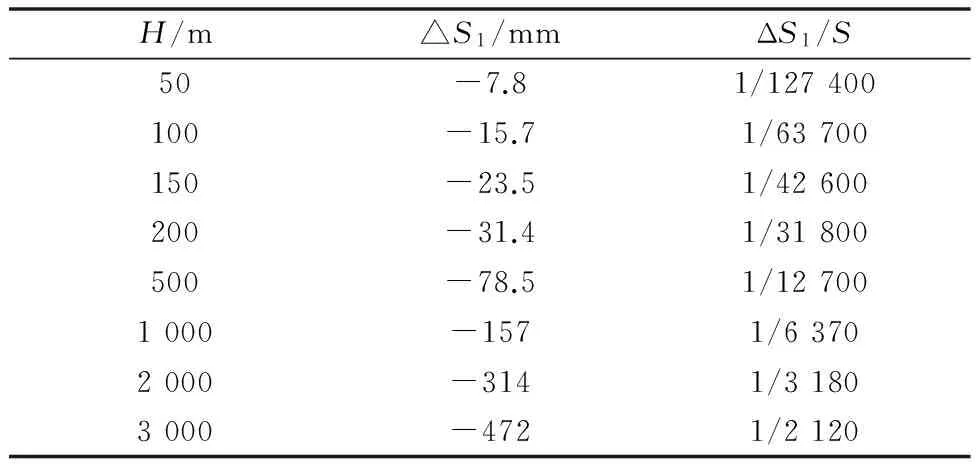
表2 不同高程面上高程投影每千米长度投影变形值和相对变形值

通过表2可知，水平边长高于椭球面时，其长度总是会减小。产生的变形量其绝对值与H成正比例关系，即H越大，变形量越大，其中当H为150 m，每千米长度变形近似达到了2.5 cm，相对变形接近1/40 000。从而解释了本项目中实测距离与反算距离之间差值超限的问题。

2) 椭球面投影到高斯平面

高斯投影是一种等角横切椭圆柱投影，投影后角度不变，中央子午线没有长度变形，向两侧长度变形逐渐增大。当ym=45 km时，每千米变形接近2.5 cm，相对变形达到1/40 000。

本项目采用1.5(°)投影带，且测区横坐标值小于10 km，可以忽略由椭球面投影至高斯平面的高斯投影变形。

3 修改全站仪格网因子抵消基线投影变形

将k503～k508连成GPS独立控制网，进行静态观测[4-5]。利用GPS后处理软件对同一GPS基线分别向0，100，200，300，400，500，600，700，800，900，1 000 m投影高程面上进行一点一方向平差，提取相邻点之间的平距[6-7]，如表3所示。

表3 各基线在不同投影高度的基线长

由表3可以看出：同一基线每100 m投影高差的平距变形值基本相等，且符合线性关系。统计0 m投影高和1 000 m投影高的平距变化量如表4所示。

表4 不同基线千米投影高差的投影变形值及相对变形值

由表3～4可以看出，每千米的基线长度在不同投影高度引起的长度变形满足线性变化的关系，且与理论推导公式的计算值基本相符。

取△S/S的平均值1/635 7，以计算单位长度单位投影高差的长度变形值，即变形系数为：

据此，在进行平面控制测量及施工放样时，可设置全站仪测距格网因子为：

S·F=1-κ×投影高度

式中，投影高度可以设定为构筑物的平均设计高程。

4 实验验证

在1号桥附近的k504(586 610.182，463 740.380，920.419 7)设站，后视k503(586 843.039，463 244.709，907.547 8)。1号桥3～7号墩为最低点，高程大致为860 m，平均高程为(860+920.419 7)/2，由全站仪测距格网因子计算公式得到下孟1号桥的测距格网因子为：

S·F=1-κ×投影高度=1-1.573 069 058×10-7×

(860+920.419 7)/2=0.999 859 96

将此格网因子输入全站仪，后视定向完成后，重新观测k503的坐标为：X=586 843.039，Y=463 244.715，只是在Y方向和理论值相差6 mm。

笔者在设定格网因子后采用全站仪测距对其余各控制点进行验证，验证结果如表5。

由表5可以看出：修改格网因子后，同一基线的观测平距和坐标推算的平距相差很小，相对精度得到显著提高，能够满足相关施工要求。

表5 修改格网因子前后相关基线观测值

5 结 语

通过上述工程案例，说明利用全站仪格网因子抵消高程改化的方法解决了投影长度变形超限的问题。该方法可以有效提高施工精度，便于操作。

[1] GJJ8-99 城市测量规范[S].北京：中国建筑工业出版社，1999.

[2] 杨国清. 控制测量学(第三版)[M]. 郑州: 黄河水利出版社，2007.

[3] 秦菊芳，胡有云，李爱华. 高等级公路测设长度综合变形问题的研究[J]. 测绘通报，2002(9)：28-30.

[4] 吴俐民，丁仁军，李凤霞. GPS参考站系统原理与应用[M].城都：西南交通大学出版社，2008.

[5] 徐绍铨，张华海，杨志强.GPS测量原理及应用(第三版)[M]. 武汉：武汉大学出版社，2008.

[6] 白建军，宋伟东，马维诺.高速公路平面控制测量中投影问题的分析[J]. 测绘科学，2006(7)：133-134.

[7] 张志刚. 线桥隧测量[M]. 成都：西南交通大学出版社，2011.

An Analysis and Processing of Projection Length Deformation in Mine Area

LIU Shun, TIAN Zhenghua

(ShanxiRailwayInstitute,Weinan,Shanxi714000,China)

Because of the projection plane choice problem, there are some problems in mine area plane control network establishment of projection deformation phenomena, inluding rules, regulations and road test area. The length deformation value shall not be more than 2.5 cm/km. In the analysis of proposed by modifying the total station grid factor, it will offset the altitude change method to reduce the projection length deformation value, which has a certain practical significance.

Plane control survey; Elevation correction; Projection deformation; Grid factor

2017-03-14

刘舜(1981-)，男，山东菏泽人，讲师，研究方向：工程测量，手机：15100115182，E-mail：546972132@qq.com.

U412

A

10.14101/j.cnki.issn.1002-4336.2017.02.054