基于MATLAB模拟小区开放对道路通行的影响

杨乾+刘婷+刘江+吴松林

摘 要：随着社会经济的不断发展及城市交通现代化水平的提高，城市交通需求不断增长，交通供需矛盾日益明显。本文从道路通行能力的微观层面，主要建立了最大服务交通量与道路拥塞密度的模型，交叉路口拥挤交通流的排队长度的模型以及道路拥塞密度与通行力之间的数学模型。旨在研究小区开放对道路通行能力的影响，从而优化路网结构，提高道路通行能力，改善交通状况。

关键词：道路拥塞密度；最大服务交通量；小区开放；道路通行

1 背景分析

改革开放以来，我国城市规划建设管理工作成就显著，城市规划法律法规和实施机制基本形成，基础设施明显改善，公共服务和管理水平持续提升，在促进经济社会发展、优化城乡布局、完善城市功能、增进民生福祉等方面发挥了重要作用。同时务必清醒地看到，城市规划建设管理中还存在一些突出问题：城市规划前瞻性、严肃性、强制性和公开性不够，城市建筑贪大、媚洋、求怪等乱象丛生，特色缺失，文化传承堪忧；城市建设盲目追求规模扩张，节约集约程度不高；依法治理城市力度不够，违法建设、大拆大建问题突出，公共产品和服务供给不足，交通拥堵等“城市病”蔓延加重。

为了积极适应和引领经济发展新常态，把城市规划好、建设好、管理好，对促进以人为核心的新型城镇化发展，建设美丽中国，实现“两个一百年”奋斗目标和中华民族伟大复兴的中国梦具有重要现实意义和深远历史意义。进一步加强和改进城市规划建设管理工作，解决制约城市科学发展的突出矛盾和深层次问题，开创城市现代化建设新局面。

2 模型假设

（1）假设小区开放后，小区内部所开设的道路不会出现交通拥挤的问题。

（2）假设政府没有采取限制车辆通行的措施，所以搜索到的数据基本准确有效，具有一定的说服力。

（3）假设所选的指标具有一定的评价能力，忽略其他要素对道路通行能力的影响。

3 模型的建立与分析

为了评价小区开放对周边道路通行的影响，选取了道路交叉路口的拥塞密度、车辆排队长度、车流量作为分析评价的指标。判断标准依据《道路工程设计规范》。K：车道组V/C即道路拥塞密度，V/C指在理想条件下，最大服务交通量与基本通行能力之比，反映交叉路口的拥塞密度指标。

K=V/C

其中：K：道路拥塞密度；V：最大服务交通量（pcu/h）；C：基本通行能力（pcu/h）。

拥塞密度的评价等级，一级，K<0.4，车流稳定，基本无延误或少量延误；二级，0.4？燮K<0.6，车流稳定，有一定的延误，但可以接受；三级，0.6？燮K<0.75，接近不稳定车流，有较大延误，但可以忍受；四级，0.75？燮K<0.9，不稳定车流，交通拥挤甚至堵塞，延误很大，无法接受。

3.1 建立车辆通行的数学模型

3.1.1 最大服务交通量与道路拥塞密度的拟合模型

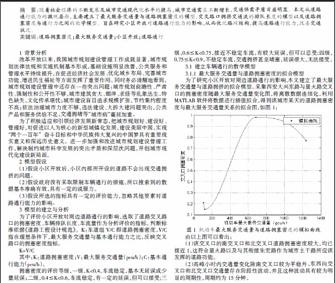
为了研究小区开放对周边道路通行的影响，本文建立了最大服务交通量与道路拥挤的拟合模型。采集西安大兴东路与星火路交叉口的拥塞密度随最大服务交通量变化图，将离散数据连续化，利用MATLAB软件将数据进行插值拟合，得到该城市某天的道路拥塞密度与最大服务交通量关系的拟合图，如图1：

由以上图可以看出：

（1）该交叉口的南交叉口和北交叉口道路拥塞密度较大，均已接近1，这符合星火路以及与其衔接朱宏路作为城市主干路所应该发挥的道路功能。

（2）高峰小时内交通量变化除南交叉口较为平稳外，东西向交叉口和北交叉口交通量存在阶段性波动，并且这种波动具有较为明显的周期性，周期约为15分鐘。

（3）南北交叉口对东西交叉口的影响较大。南北方向作为城市交通主干路，其进口交通量微小的波动即造成东西向交通量较大的波动。

引入道路拥塞密度K：

K=V/C

接着，用道路拥塞密度进行相应的等级划分，分别带入各最大服务交通量数据，求出该交叉口的道路拥塞密度。

3.1.2 交叉路口拥挤交通流的车量排队长度模型的建立

由交通流理论知道，流量z-拥塞密度K曲线可以表示为二次抛物线型，当拥塞密度取得最佳值km时，流量达到最大值zm，以km为界，交通流状态被划分为非拥挤和拥挤两种状态。

所以可建立拥挤交通流的车量排队长度模型，来研究车辆排队长度与交叉路的基本通行能力，平均延误时间，入口车流量间的关系。

y0+y1（t）=y2（t）+？驻y（t）（1）

式中y0：初始时间（t=0）入口与交叉路口的车辆数；

y2（t）：时刻t通过交叉路口的车辆累计数；

y1（t）：时t刻通过入口的车辆累计数；

？驻y（t）：时刻t入口与交叉路口之间的车辆数。

假设正常行驶交通流的密度为最佳密度，根据二流理论， ？驻y（t）又可以由下式计算得到：

式中：L：入口与交叉路口之间的距离；

km：入口与交叉路口之间的交通流最佳密度；

kj：入口与交叉路口车流量之间的交通流阻塞密度；

L2（t）：时刻t入口与交叉路口之间的车量排队长度。

（3）

为了分析公式（3）的适用条件，令k（t）表示时刻t入、出口之间的平均交通流密度，则k（t）=（y0+y1（t）-y2（t））/L。

（1）从宏观交通流的角度来分析流量-密度曲线：当0？燮k（t）？燮km时，入、出口之间交通流处于非拥挤状态；当k（t）=km时，入、出口之间交通流处于最佳通行状态；当km

（2）实际上，车辆排队长度不可能小于零，也不可能超过路段长，即0？燮L2（t）？燮L。当y0+y1（t）-y2（t）=kjL时，L2（t）=L，此时车量排队长度取得最大值，即等于路段长度；当y0+y1（t）-y2（t）=kmL时，L2（t）=0，此时车量排队长度取得最小值，即恰好没有排队，入、出口之间交通流以最佳密度运行。