层间状态对沥青路面力学性能与疲劳寿命影响研究

陈亚章， 吕继群

(1.湖南省郴州公路桥梁建设有限责任公司, 湖南 郴州 423000; 2.浙江建设职业技术学院, 浙江 杭州 311231)

层间状态对沥青路面力学性能与疲劳寿命影响研究

陈亚章1， 吕继群2

(1.湖南省郴州公路桥梁建设有限责任公司, 湖南 郴州 423000; 2.浙江建设职业技术学院, 浙江 杭州 311231)

层间结合状态是影响沥青路面力学性能与使用性能的重要因素。鉴于目前我国沥青路面设计规范中层间完全连续且不产生相对滑移假定的缺陷，采用BISAR3.0软件中的简化剪切弹性柔量ALK来描述层间结合状态，并以水平荷载和竖向荷载共同作用作为加载方式，得到相应的沥青路面力学响应，同时对沥青路面疲劳寿命进行预估。结果表明：层间结合状态的退化对沥青层底弯拉应力、弯拉应变与剪应力影响较大，而对路表弯沉影响较小；层间结合的弱化对沥青路面疲劳寿命影响显著。

沥青路面; 层间状态； 简化剪切弹性柔量； 水平荷载； 力学性能； 疲劳寿命

半刚性基层沥青路面是一种典型的路面结构，在我国高等级公路中应用广泛。由于路面采用分层铺筑，层间结合处置方法的不成熟导致层间结合状态与现行我国沥青路面设计规范中层间完全连续的假定[1]存在一定差异。实践表明：实际沥青路面的层间结合状态介于完全连续与完全光滑之间，是一种半结合状态[2]。因此层间状态就成为了沥青路面设计与施工中的薄弱环节，既影响了沥青路面的力学性能，同时层间结合状态退化引起的路面早期病害，也降低了路面的使用性能[3,4]。

对于非完全连续的层间结合状态，水平荷载的存在会进一步削弱层间的结合。鉴于此，本文采用BISAR3.0软件中的简化剪切弹性柔量ALK来表征不同的层间结合状态[5]，同时以水平荷载与竖向荷载共同作用作为加载方式，计算不同层间结合状态下的力学响应，并对沥青路面的疲劳寿命进行预估[6]。

1 路面结构与计算模型

根据我国沥青路面设计规范以及半刚性基层路面结构形式，选取的沥青路面典型结构及各层的物理、力学参数见图1。加载方式： 竖向为标准轴载BZZ — 100 kN的双圆均布荷载，当量圆直径为21.3cm，两荷载圆圆心间距为31.95 cm；水平向为摩擦系数0.3、与行车方向相同的单轮7.5 kN的水平荷载。

图1 沥青路面结构形式及参数

2 层间状态理论描述

对于层间非连续状态的描述，主要有2种模型：一是库仑摩擦模型，二是Goodman模型。BISAR3.0中的简化剪切弹性柔量ALK就是以Goodman模型为基础，通过层间的水平剪切力与相对位移的关系来描述层间接触问题。将相邻两层的分界面看成是一个无限薄的内层，ALK就可表示成：

(1)

式中: ALK为简化剪切弹性柔量，m；E为层间界面上层的弹性模量，MPa；μ为该层的泊松比；AK为标准剪切弹性柔量，m3/N，它定义为界面薄层上相对水平位移的大小与作用面上剪应力大小的比值，即：

(2)

式中: ΔU为层间相对水平位移，m；τ为作用在层间界面上的剪应力，MPa。

研究表明， 当ALK从0到100r(r为荷载半径，见图1)之间大量取值时就包括了层间完全连续到完全光滑的所有情况[7]。鉴于半刚性基层沥青路面面层与基层的结合状态是影响路面力学性能与使用性能的关键因素，本文假定其他各层间均为完全连续状态，只考虑沥青面层与基层间的结合状态变化，所取参数值见表1。同时取距轮隙中心分别为0、0.053 25、0.15975、0.26625 m的4个点位(图1中的A、B、C、D)来计算路面力学响应。

表1 基—面层间状态参数值层间状态ALK/m完全连续0半结合0.1、0.25、0.5、1、5完全滑动10.65

3 力学响应计算结果及分析

3.1 层间状态对弯拉应力的影响

在水平荷载与竖向荷载共同作用下，不同层间结合状态的沥青面层底部弯拉应力变化曲线如图2所示，各状态的最大弯拉应力值及变化率见表2。

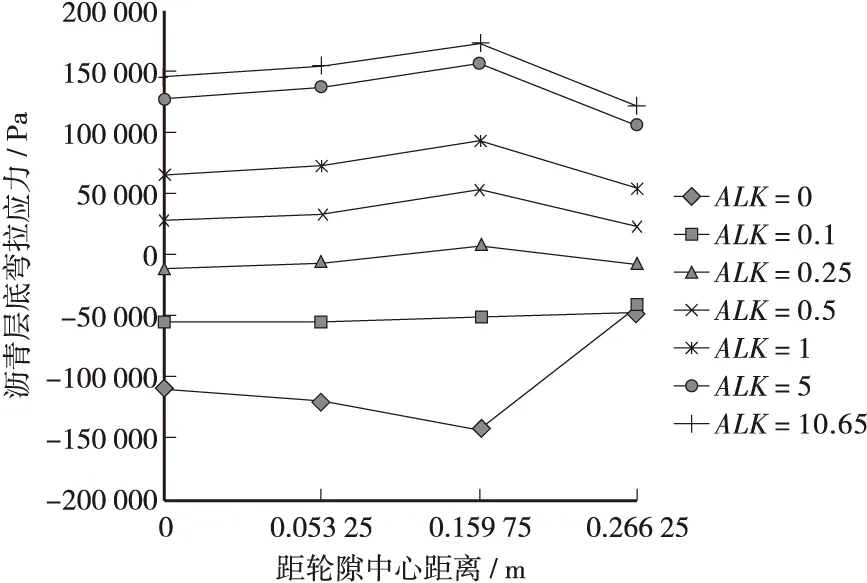
图2 沥青层底弯拉应力变化图

由图2可知，当基 — 面层间状态ALK=0和0.1时，沥青层底为压应力，随着层间结合状态的退化，沥青层底逐渐由压应力转变为拉应力。当ALK=0.25 m时，荷载中心处率先出现拉应力，当ALK超过0.25 m后，4个计算点位均为拉应力；同时，随着层间结合状态的退化，荷载中心处逐渐由下凹变为上凸，即由最安全退化为最不利，退化速度最快。

由表2所列结果可知，随着层间结合状态的退化，沥青层底最大弯拉应力逐渐由压应力变为拉应力，且层间完全光滑时沥青层底最大弯拉应力较完全连续时增大了501.71%。因此，层间结合状态的退化对沥青层底弯拉应力影响较为显著。

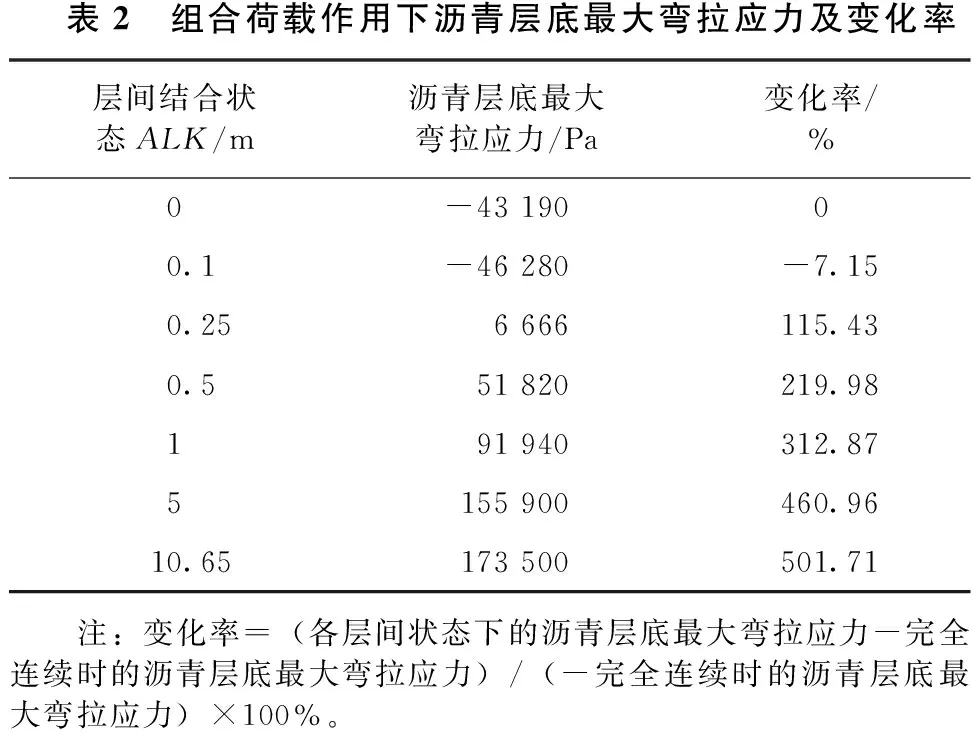
表2 组合荷载作用下沥青层底最大弯拉应力及变化率层间结合状态ALK/m沥青层底最大弯拉应力/Pa变化率/%0-4319000.1-46280-7.150.256666115.430.551820219.98191940312.875155900460.9610.65173500501.71 注:变化率=(各层间状态下的沥青层底最大弯拉应力-完全连续时的沥青层底最大弯拉应力)/(-完全连续时的沥青层底最大弯拉应力)×100%。

3.2 层间状态对弯拉应变的影响

在组合荷载作用下，不同层间结合状态的沥青面层底部弯拉应变变化曲线如图3所示，各状态的最大弯拉应变值及变化率见表3。由图3可知，当基-面层间完全连续时,沥青层底弯拉应变最小，当ALK=0.1时，沥青层底弯拉应变就出现了较大的增加，说明沥青层底弯拉应变对层间结合状态改变的反应较为敏感。同时，随着层间结合状态的退化，沥青层底弯拉应变逐渐增大，且在各种层间状态下，荷载中心处的弯拉应变均为最大。

图3 沥青层底弯拉应变变化图

从表3所列结果可以看出，当层间完全连续时，沥青层底最大弯拉应变只有7.75με，但当ALK=0.1时，沥青层底最大弯拉应变就变成了52.78με，增长了581.47%。当层间完全光滑时，沥青层底最大弯拉应变则变成了165.60με，较完全连续时增大了2038.15%。因此，层间结合状态的退化对沥青层底弯拉应变影响非常显著，同时，弯拉应变对层间状态改变的响应也非常敏感。

表3 组合荷载作用下沥青层底最大弯拉应变及变化率层间结合状态ALK/m沥青层底最大弯拉应变变化率/%07.75με00.152.78με581.470.2582.09με959.910.5105.10με1257.011125.50με1520.405157.20με1929.7010.65165.60με2038.15 注:变化率=(各层间状态下的沥青层底最大弯拉应变-完全连续时的沥青层底最大弯拉应变)/(完全连续时的沥青层底最大弯拉应变)×100%,下同。

3.3 层间状态对剪应力的影响

在水平荷载与竖向荷载共同作用下，不同层间结合状态下的沥青面层底部剪应力变化曲线如图4所示，各状态的最大剪应力值及变化率见表4。

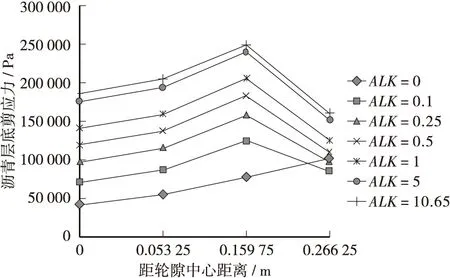
图4 沥青层底剪应力变化图

由图4可知，随着层间结合状态的退化，沥青层底剪应力逐渐增大，且除了层间完全连续状态外，各层间结合状态下的荷载中心处剪应力均为最大。剪应力的增大会进一步削弱层间结合状态，在反复荷载作用下，引起沥青路面的早期病害。

从表4的计算结果可以看出，随着层间结合状态的退化，沥青层底最大剪应力增大的较为均匀，层间完全光滑时的沥青层底最大剪应力较完全连续时增大了144.86%。因此，层间结合状态的退化对沥青层底剪应力影响较大，但不会出现突增现象。

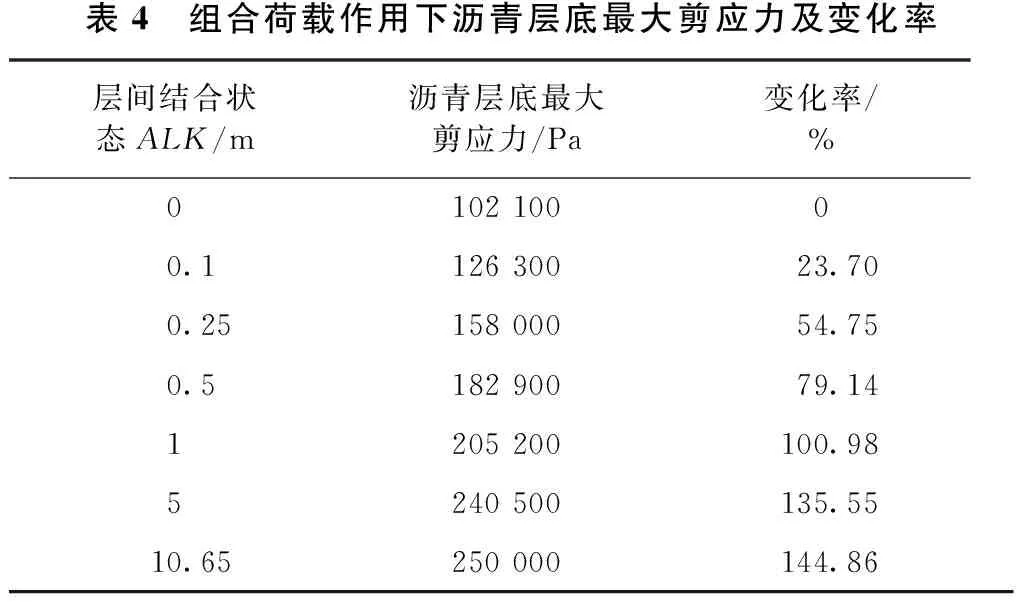
表4 组合荷载作用下沥青层底最大剪应力及变化率层间结合状态ALK/m沥青层底最大剪应力/Pa变化率/%010210000.112630023.700.2515800054.750.518290079.141205200100.985240500135.5510.65250000144.86

3.4 层间状态对路表弯沉的影响

在组合荷载作用下，不同层间结合状态下的沥青路面路表弯沉值变化曲线如图5所示，各状态下的最大路表弯沉值及变化率见表5。本文为了计算上的通过，同时为了兼顾精确度，选取距路表0.1 mm 4个计算点位的弯沉值来近似代替路表弯沉值。

由图5可知，随着层间结合状态的退化，沥青路面路表弯沉值逐渐增大，且在各结合状态下，荷载中心处的路表弯沉值均为最大。在长期荷载作用下，较大的路表弯沉值会引起沥青路面的车辙病害，降低路面的使用性能。

由表5的计算结果可见，随着层间结合状态的退化，沥青路面路表最大弯沉值逐渐增大，但层间完全光滑时的路表最大弯沉值较完全连续时仅增大了16.55%。因此，层间结合状态的退化对沥青路面路表弯沉值影响较小。

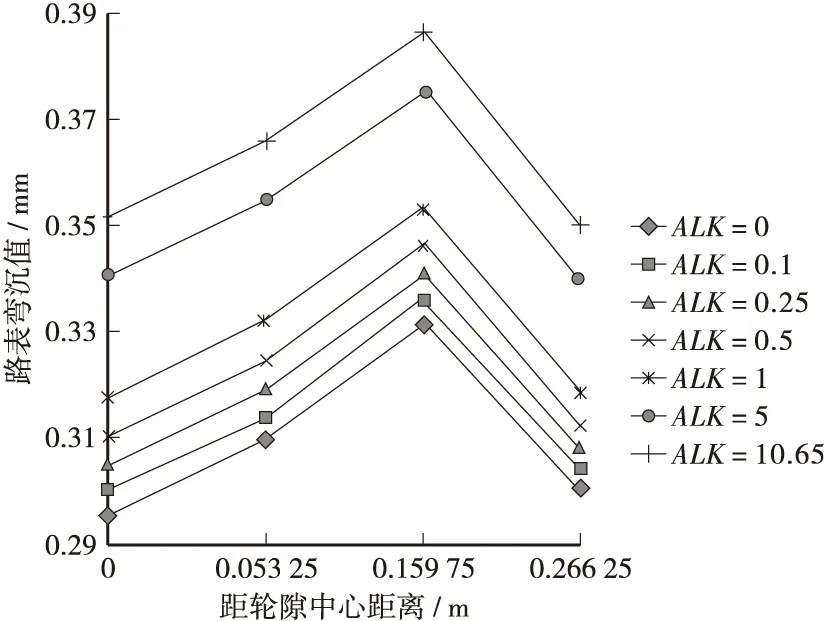
图5 路表弯沉值变化图

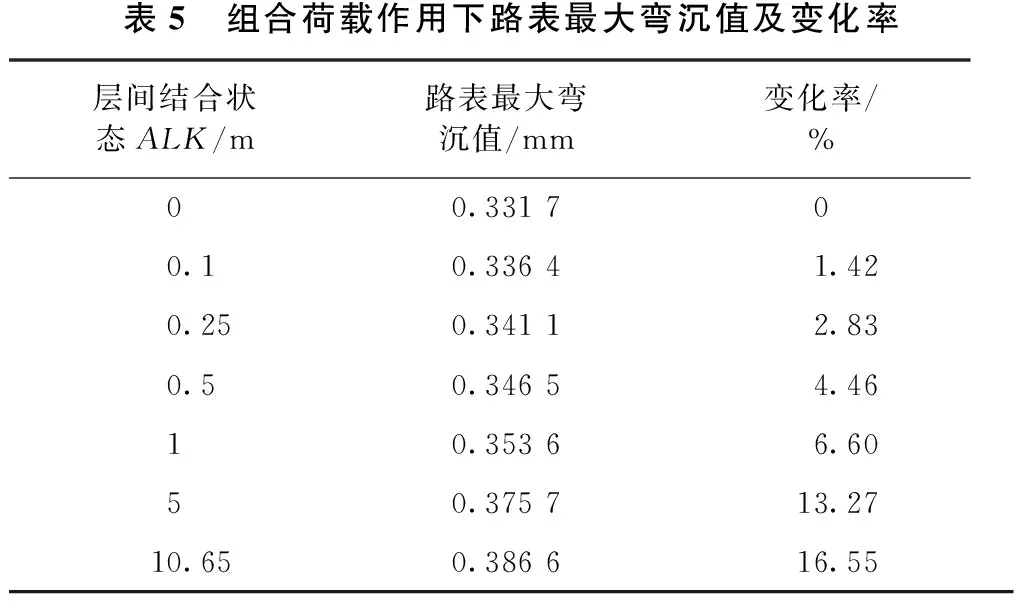
表5 组合荷载作用下路表最大弯沉值及变化率层间结合状态ALK/m路表最大弯沉值/mm变化率/%00.331700.10.33641.420.250.34112.830.50.34654.4610.35366.6050.375713.2710.650.386616.55

4 沥青层底疲劳寿命分析

疲劳破坏是沥青路面主要破坏形式之一，沥青路面的疲劳寿命是指达到临界破坏状态时沥青路面所能承受的标准轴载作用次数。层间结合状态的改变会引起沥青路面应力重分布，从而影响沥青路面的疲劳寿命。根据我国沥青路面设计规范，当以沥青层底拉应力为控制指标时，疲劳寿命为：

(3)

式中:Ne为路面容许作用的疲劳次数，次；σS为沥青混凝土的极限劈裂强度，MPa；σR为路面结构层材料的容许拉应力，MPa。

将表2的计算结果带入式(3)得到以沥青层底弯拉应力为控制指标的疲劳寿命见表6。由于在ALK=0和0.1时沥青层底为压应力，因此对这2种情况不予计算。由表6的计算结果可知，层间结合状态退化初期，沥青层底疲劳寿命降低较快，之后逐渐减小；层间完全光滑时，疲劳寿命较初期减

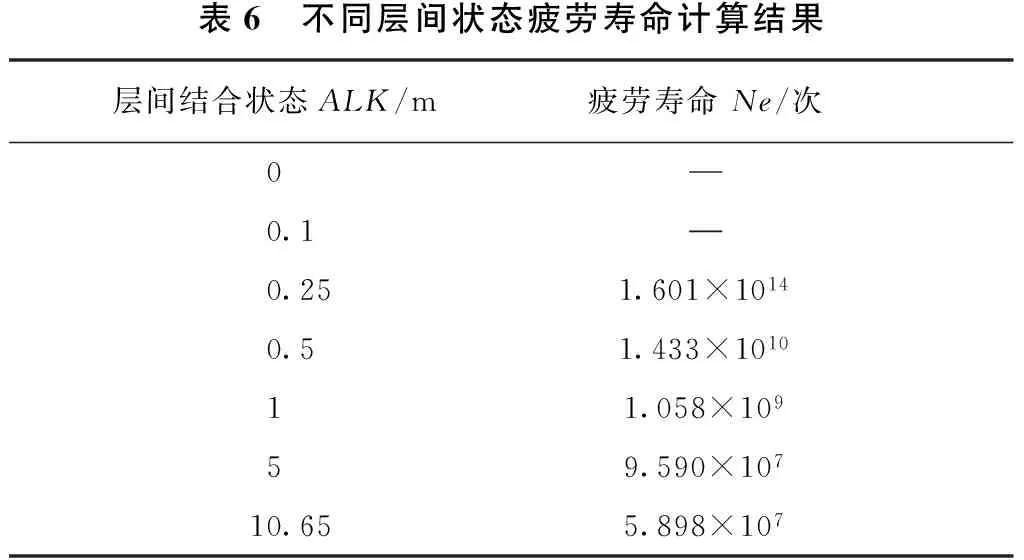
表6 不同层间状态疲劳寿命计算结果层间结合状态ALK/m疲劳寿命Ne/次00.10.251.601×10140.51.433×101011.058×10959.590×10710.655.898×107

小了7个数量级。

结合国外研究资料，当以沥青层底弯拉应变为控制指标时，疲劳寿命为：

(4)

式中:Nf为路面容许作用的疲劳次数，次；k1、k2为由疲劳试验确定的参数。

国外研究资料表明，参数k2的变化范围为3.17～6.13，平均值为4.36；k1的变化范围为3.98×10-15～1.247×10-7，且k1与k2存在着一定的函数关系：

k2=-0.3269lgk1+1.1857

(5)

本文中取平均值k2=4.36，则k1=1.9485×10-10。

将表3的计算结果代入式(4)得到以沥青层底弯拉应变为控制指标的疲劳寿命见表7。

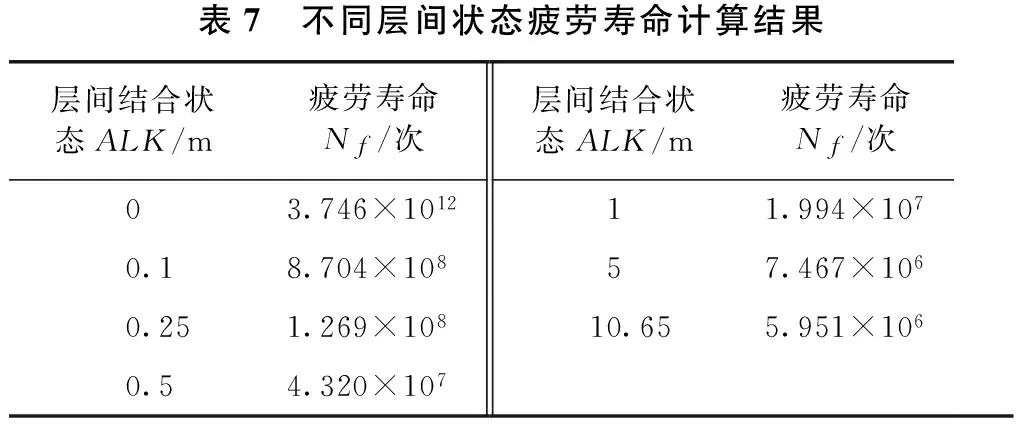
表7 不同层间状态疲劳寿命计算结果层间结合状态ALK/m疲劳寿命Nf/次层间结合状态ALK/m疲劳寿命Nf/次03.746×101211.994×1070.18.704×10857.467×1060.251.269×10810.655.951×1060.54.320×107

从表7的计算结果可以看出，虽然以沥青层底弯拉应变为控制指标的疲劳寿命与弯拉应力存在一定的差异，但疲劳寿命随层间结合状态退化的变化规律基本相同，均是初期疲劳寿命降低较快，之后逐渐减小，且层间完全光滑时的疲劳寿命较完全连续减小了多个数量级。

由2种控制指标的疲劳寿命计算结果均可以看出，层间不良结合状态会引起沥青路面疲劳寿命的大幅度降低。因此，在反复载荷作用下，层间不良结合状态将会引起沥青层底过早地出现疲劳开裂。

5 结论

本文以简化剪切弹性柔量ALK来描述层间结合状态，得到了水平荷载与竖向荷载共同作用时不同层间状态的力学响应，并分别以沥青层底弯拉应力与弯拉应变作为控制指标，计算出相应的沥青层底疲劳寿命，主要结论如下：

1) 层间结合状态的退化对沥青层底弯拉应力、弯拉应变以及剪应力影响较大，而对路表弯沉影响较小。

2) 虽然以2种控制指标计算得到的沥青层底疲劳寿命存在一定差异，但均反映出层间结合状态的退化对沥青层底疲劳寿命影响较大，且初期降低较快，之后逐渐减小。

3) 层间结合状态的退化对沥青路面力学性能及疲劳寿命影响显著，因此，在设计和施工中应充分重视基 — 面层的粘结问题，采取合理的施工材料及工艺，提高路面的使用寿命和服务水平。

[1] JTG D50 — 2006,公路沥青路面设计规范[S].

[2] Hu Xiaodi, Walubita L F. Effects of Layer Interfacial Bonding Conditions on the Mechanistic Response in Asphalt Pavement[J]. Journal of Transportation Engineering,2011,137(1):28-36.

[3] 龚红仁，邹晓翎,等.层间状态对沥青路面疲劳开裂与位移的影响[J].武汉理工大学学报，2012,34(12)：66-70.

[4] Sutanto M H. Assessment of Bond Between Asphalt Layers [D].Nottingham: The University of Nottingham, 2009.

[5] 张久鹏,武书华,裴建中，等.基于剪切弹性柔量的基-面层间接触状态及路面力学响应分析[J].公路交通科技,2013,30(1):6-11,16.

[6] 朱耀庭,雷茂锦,时宁,等.层间结合状态对沥青路面结构力学和寿命影响分析[J].公路工程,2011,36(5): 18-21,32.

[7] Bitumen Business Group. BISAR3.0 User Manual [M].The Hague: Shell International Oil Products B V,199.

2016-11-08

陈亚章( 1982-) ，男，工程师，主要从事路桥施工。

1008-844X(2017)01-0088-04

U 416.217

A