压缩打捆机构及曲柄模态与谐响应分析

郭振华，陈换美，张立新

（1石河子大学机械电气工程学院，新疆 石河子 83200；2巴音郭楞职业技术学院，新疆 库尔勒 841000）

0 引言

我国具有丰富的芦苇等粗纤维资源，可用于造纸、建材、饲料、医药等行业[1]。然而，由于芦苇密度低，致使其运输成本较高，愿意承担芦苇运输的车辆很少。芦苇打捆装备可以有效解决芦苇等原料运输过程中产生的亏吨问题，对降低企业生产成本具有非常重要的作用。但是，在打捆装备的工作过程中，机械振动不可避免。打捆机构在一定的振动频率范围内容易产生共振现象，导致关键构件发生结构损伤，影响对芦苇的压缩效果。本文针对打捆机的核心机构——压缩曲柄滑块机构及曲柄进行模态分析和谐响应分析，为打捆机的设计提供理论参考。

1 模态分析理论

模态分析是将系统的振动微分方程组中的物理坐标变换为模态坐标，通过方程组解耦，求出系统的模态参数，使其成为用模态坐标和模态参数描述的独立方程[2]。

（1）式为N自由度的线性振动表达式。式中：[M]为系统的质量矩阵；[C]为系统的阻尼矩阵；[K]为系统的刚性矩阵；x''为系统加速度；x'为速度；x为位移；F（t）为系统激振力。

模态分析分为自由模态分析和约束模态分析。自由模态是指在不考虑任何约束情况下得到的系统本身固有特性。自由模态是模态分析的重要组成部分，通过自由模态分析，可以对系统自身的尺寸、材料、振动等固有特性有必要了解。约束模态则是指系统在受约束情况下的模态分析[2]。

对系统进行自由模态分析时，设定系统在振动时不受外力，即F（t）=0。此时，系统内部阻尼较小，在分析系统自由振动的频率和振型时可忽略不计。得到系统无阻尼振动微分方程：

该方程特解为：

（3）式中，Φ表示自由响应幅值矩阵。将式（3）代入式（2）中，可得特征方程：

（4）式中，ωi表示第i阶固有频率。

经过上述变换，将系统固有频率和振型问题转变成求解方程特征值问题。方程（4）有非零解的充要条件为：

应用分块兰索斯法（Block Lanczos）将方程（5）变换为对角矩阵，采用追赶法求解，可得n个不同正解ωoi（i=1，2，…n）。

ωoi表示系统第i阶固有频率。

2 压缩曲柄滑块机构模态仿真分析

偏置式曲柄滑块机构是压缩打捆机核心部件，该部件的刚度、强度及其力学特性决定整机的使用寿命。通过对打捆机曲柄滑块机构进行有限元模态分析，得出其在工作状态下的固有频率和振型，可以为避免共振现象的产生提供数据支持。

2.1 建立有限元模型

有限元分析软件abaqus自带三维建模功能，但是建模过程繁琐，并且精度较低。为提高建模效率，应用专业三维建模软件Solidworks对压缩曲柄滑块机构进行建模，然后将建好的三维模型导入abaqus中进行分析。建模过程中，为减少计算时间提高分析效率，可以在不影响分析效果的前提下对模型进行简化，如，忽略圆角倒角等对有限元分析结果影响不大的结构特征。

具体步骤如下：（1）应用三维软件建立打捆机曲柄滑块机构的三维模型；（2）将建成的三维模型另存为Para solid格式，并导入abaqus软件中；（3）在abaqus环境下设置模型材料，具体设置如表1所示。（4）划分网格：网格划分类型采用0.008 mm四面体，结果如图1所示。（5）对网格划分结果进行检测，结果如表2所示，表明网格划分结果满足模态分析要求。

表1 材料属性Tab1 Material properties

表2 单元质量Tab2 Quality of elements

2.2 仿真结果及分析

模态分析提取阶数设置为5阶，扩展阶数设置为5阶，频率区间设置为0—3 000 Hz。

在上述参数设置下，对曲柄滑块机构进行约束模态分析，仿真结果如下。

图1 压缩曲柄滑块机构的网格划分图Fig1 The finite element mesh of compression packing mechanism

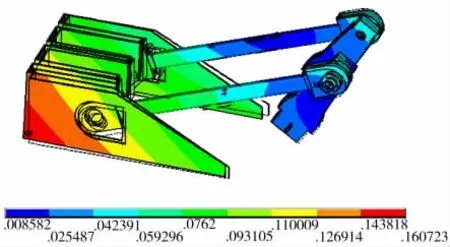
图2 模态云图第3阶Fig2 The Modes Modal diagram of the 3st stage

图3 模态振型云图第4阶Fig3 The Modes Modal diagram of the 4st stage

图4 模态振型云图第5阶Fig4 The Modes Modal diagram of the 5st stage

前5阶固有频率和振型描述如表3所示。

分析结果可知：（1）在前5阶模态仿真结果中，1阶模态和2阶模态固有频率为0或近似为0，可认为结构基本无变形，表现为刚性。（2）3阶至5阶的模态云图表明，曲柄滑块机构发生明显的变形和位移。其中，曲柄的变形较明显，故对曲柄进行单独的模态分析。

表3 前5阶固有频率和振型描述Tab3 The first 5 description of free frequencies and mode shapes

3 压缩曲柄的模态仿真分析

通过对曲柄进行网格划分和模态分析，得到曲柄5阶约束模态云图，结果如图5—9所示。

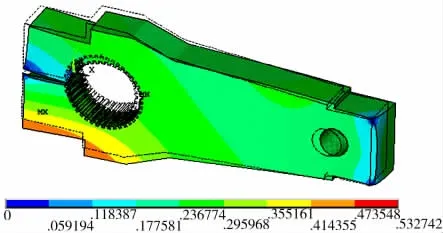
图5 模态云图第1阶Fig5 The Modes Modal diagram of the 1st stage

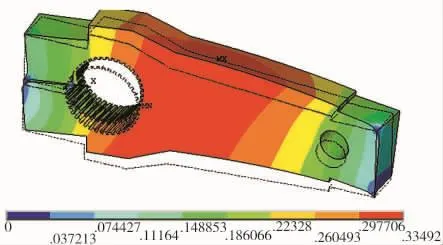
图6 模态云图第2阶Fig6 The Modes Modal diagram of the 2st stage

图7 模态云图第3阶Fig7 The Modes Modal diagram of the 3st stage

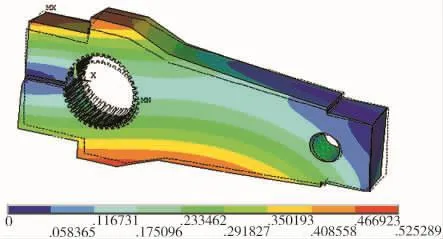
图8 模态云图第4阶Fig8 The Modes Modal diagram of the 4st stage

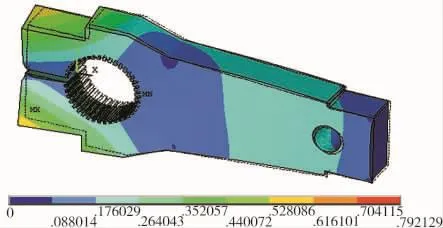
图9 模态云图第5阶Fig9 The Modes Modal diagram of the 5st stage

曲柄的5阶模态分析云图描述如表4。

表4 曲柄前5阶模态描述Tab4 The first 5 description of free frequencies and mode shapes

通过上述分析可知，曲柄的5阶模态固有频率分别为6.71 Hz、19.68 Hz、28.89 Hz、116.73 Hz、255.63 Hz。为避免共振现象的发生，在打捆机工作状态下，应避免出现上述频率。打捆机的工作频率可由式（7）表达。

（7）式中，f表示激振频率；n表示动力输出轴转速；δ表示误差系数。

通过式（7）可求得不同频率下对应的输出轴转速，如表5所示。

表5 转速对应表Tab5 The corresponding table of rotational speed

根据国家标准，拖拉机动力输出轴转速范围为540—1 000 r/min。对应表5，为避免共振现象的产生，发动机转速应尽量避免540.5—640.5 r/min和816.6—916.6 r/min两个转速范围的使用。

4 谐响应分析

谐响应分析用于确定线性结构在承受随时间按正弦（简谐）规律变化的载荷时的稳态响应，分析过程中只计算结构的稳态受迫振动，不考虑激振开始时的瞬态振动。谐响应分析的目的在于计算出结构在几种频率下的响应值对频率的曲线，从而能预测结构的持续性动力特性，验证设计是否能克服共振、疲劳以及其他受迫振动引起的有害效果[2，6，8]。压缩打捆机曲柄的模态分析反映了系统本身的振动属性，谐响应分析可以反映其在实际工作环境下的振动响应。

4.1 谐响应参数设置

通过模态分析可以得到压缩曲柄滑块机构曲柄的固有频率范围为0—256 Hz，故选取0—500 Hz为机构的激振范围，设置载荷步为200，在曲柄端施加幅值为3 000 N的简谐载荷。根据所得的约束模态振型，提取3处关键点进行响应分析，分别取机构中关键点23、41、43。关键点的位移响应如图10和图11所示。

图10 Y平面内谐响应分析云图Fig10 The char of Harmonic analysis in Y plane

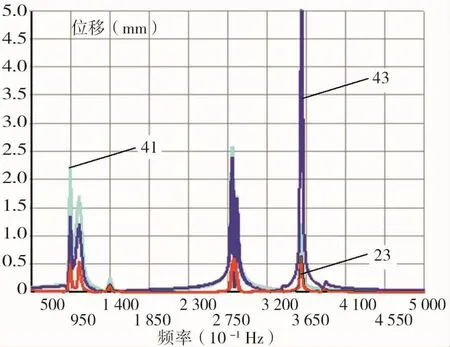
图11 Z平面内谐响应分析云图Fig11 The char of Harmonic analysis in Z plane

4.2 仿真结果及分析

通过对响应云图10和图11的分析可知，当振动频率为100.80 1Hz、126.11 Hz、278.60 Hz、321.93 Hz（舍去）、350.35 Hz（舍去）时，曲柄易发生共振现象。其中，最大谐峰值出现在第4阶和第5阶。可见，在压缩打捆机工作过程中，不同的振动频率将会产生不同振幅，振幅过大会影响压缩效果，甚至对设备产生一定的破坏。

5 结论

通过对压缩打捆机曲柄滑块机构及曲柄进行模态分析和谐响应分析得到以下结论：（1）曲柄滑块机构的前5阶模态中，1阶和2阶模态表现为刚性，3阶至5阶模态中曲柄滑块机构表现出明显的位移和变形，其中曲柄表现较明显；（2）曲柄的5阶模态固有频率分别为6.71Hz、19.68Hz、28.89Hz、116.73Hz、255.63Hz，在固有频率下曲柄的上下端面易发生变形，5阶模态下发生扭曲变形。为避免共振现象的产生，发动机转速应避免540.5—640.5 r/min和816.6—916.6 r/min两个转速范围的使用。（3）谐响应分析表明，当振动频率为100.81 Hz、126.11 Hz和278.6 Hz时，曲柄将发生共振现象。其中，最大谐峰值出现在第4阶和第5阶。

References

[1]王振庆，王丽娜，吴大千，等.中国芦苇研究现状与趋势.山东林业科技，2006（6）：85-87，74.Wang Z Q，Wang L N，Wu D Q，et al.The actuality and trend in the study of phragmites australis（Cav.）Trin.ex Steud.in China.Journal of Shandong Forestry Science and Technology，2006（6）：85-87，74.（in Chinese）

[2]梁君，赵登峰.模态分析方法综述.现代制造工程，2006（8）：139-141.Liang J，Zhao D F.Summary of the model analysis method.Modern Manufacturing Engineering，2006（8）：139-141.（in Chinese）

[3]陆秋海，李德葆.模态理论的进展.力学进展，1996（4）：464-472.Lu Q H，Li D B.The advances of modal theory.Advances in Mechanics，1996（4）：464-472.（in Chinese）

[4]张翔，张立新，成斌，等.粗纤维压缩打捆机构模态与谐响应分析.农机化研究，2015（4）：23-26，39.Zhang X，Zhang L X，Cheng B，et al.The modal and harmonic response analysis of the baling compression mechanism for crude agricultural fibers.Journal of Agricultural Mechanization Research，2015（4）：23-26，39.（in Chinese）

[5]刘昌领，陈建义，李平.基于 ANSYS的六缸压缩机曲轴模态分析及谐响应分析.流体机械，2012（8）：17-21，26.Liu C L，Chen JY，Li P.Modal and harmonic response analy sis of crankshaft of a six cylinders compressor by ANSYS.Fluid Machinery，2012（8）：17-21，26.（in Chinese）

[6]骆洪亮.轴向柱塞泵表面振动分布特性谐响应及瞬态响应分析.燕山大学，2014.Luo H L.The Harmonic Response and Teansient Response Analysis of Axial Piston Pump Surface Vibration Haracteristics.Yanshan University，2014.（in Chinese）

[7]陈洋，陈国达，计时鸣，等.变电站避雷针杆模态及谐响应分析.机电工程，2017（2）：178-183.Chen Y，Chen G D，Ji S M，et al.Modal and harmonic response analysis of substation lightning rod.Mechanical & Electrical Engineering Magazine，2017（2）：178-183.（in Chinese）

[8]刘涛，王卫辉，鹿飞，等.基于 Workbench的箱形伸缩臂模态及谐响应分析.制造业自动化，2015（4）：80-82，97.Liu T，Wang W H，Lu F，et al.The model and harmonic response analysis of trunk telescopic boom by Workbench.Manufacturing Automation，2015（4）：80-82，97.（in Chinese）

[9]翟正锟，崔俊杰，李红梅，等.鹅颈式半挂车车架有限元模态及谐响应分析.甘肃农业大学学报，2014（2）：160-164，169.Zhai Z K，Cui J J，Li H M，et al.Finite element modal and harmonic response analysis of gooseneck type semi-trailer frame.Journal of Gansu Agricultural University，2014（2）：160-164，169.（in Chinese）

[10]刘昌领，罗晓兰.基于ANSYS的六缸压缩机连杆模态分析及谐响应分析.机械设计与制造，2013（3）：26-29.Liu C L，Luo X L.The modal and harmonic response analysis of connection rod of a six cylinders compressor by ANSYS.Machinery Design & Manufacture，2013（3）：26-29.（in Chinese）