基于可观测性分析的计及DG不确定性配电网表计优化配置

季 宇 ，孙彦萍 ，吴 鸣 ，李 洋 ，李 虹 ，梁海峰

（1.中国电力科学研究院，北京 100192；2.华北电力大学 电力工程系，河北 保定 071003）

0 引言

通过发展智能配电网自动化，增加对配电网的监控手段，智能地控制和平衡新能源的接入是未来电网发展的重心。而配电网的不可观测性严重制约了配电网自动化及智能电网的发展［1］。因此，需要对配电网的全面可观测性进行研究。输电网的可观测性算法主要有数值算法［2-3］和拓扑算法［4-5］，而针对配电网量测缺乏、量测冗余度较低的特点，为了达到可观测的目的，需要增加伪量测或者配置表计以获得足够的量测量［6-7］。伪量测一般由负荷历史数据预测得到，由于可用数据不足、数据准确性不够，伪量测的引入会带来较大的误差且不能完全解决可观测性问题［6］，所以需要配置一些量测表计来校正预测数据，从而可以更好地进行可观测性分析和状态估计。但从经济性角度考虑，在配电网中大量配置表计是不现实的，所以安装量测装置应该在有限量测装置数目的情况下选择最优配置点，即进行表计的优化配置以满足可观测性的需求。

另外，随着分布式电源DG（Distributed Generation）广泛接入配电网系统，配电网的监测和控制手段变得更加复杂，所以深入分析配电系统的特点，改进现有的可观测性分析和量测优化配置算法是很有必要的。围绕含DG配电网的量测配置问题已有很多研究［8-13］：文献［8］将不同类型的 DG 等效成不同类型的节点，处理为能够提供不同信息的实时量测，参与量测岛合并；文献［9］对未配置实时量测的DG提出了一种添加伪量测的可行方案；文献［10］将DG看作一般的PQ注入节点，并没有建立DG详细的物理模型；文献［11］为了容纳更大容量DG的接入，将DG处理成恒定功率因数的“负”的负荷，提出采用启发式方法选择配置电压测量装置的最优方案，以达到使未配置电压测量装置的节点电压估计值标准差最小的目的；文献［12］将DG出力看作伪量测，但忽略了DG出力不确定性的影响；文献［13］扩展了文献［12］的工作，利用高斯混合模型 GMM（Gaussian Mixture Model）模拟DG出力的不确定性，进行表计的优化配置。上述量测配置的研究都是从状态变量的约束入手，没有对系统的可观测性进行详细研究。本文从配电网的可观测性分析入手，由对含DG配电网可观测性的分析得到表计的配置原则。然后，以配置表计的经济性和量测区域之间负荷的均衡度为衡量指标进行表计的优化选择。而DG出力的随机性和不确定性会影响量测区域负荷的均衡，所以在优化算法中采用拉丁超立方抽样（LHS）技术处理DG出力的不确定性。最后，结合算例验证了所提算法的有效性。

1 含DG配电网的可观测性分析

将配电网中所有用户划分为N类，包括常规负荷和DG。DG看作特殊的“负”的负荷，本文假设其包含光伏 PV（PhotoVoltaic）和风电 WTG（Wind Turbine Generation）2类，每类负荷的变化规律用典型负荷模式［14-15］表示，且根据用户负荷平均功率的大小来表示用户的重要等级程度。在期望网络结构［16］下优先配置支路功率量测，求解量测方程得到N类典型负荷模式，从而获得各用户负荷，使配电网可观测。

在配置支路量测时忽略网络损耗，则有如式（1）所示的量测方程。

其中，Zt为M×1阶向量，M为量测区域的个数，元素Zt（m）（m=1，2，…，M）为 t时刻第 m 个量测区域的量测功率；H为M×N阶常系数矩阵，N为用户负荷分类数，元素 hmn（m=1，2，…，M；n=1，2，…，N）为在第m个量测区域中第n类用户负荷的平均功率总和；Xt为 N×1 阶向量，元素 xt（n）（n=1，2，…，N）为 t时刻第n类用户规格化的典型负荷模式；HXt为M×1阶向量，是Zt量测的计算值，所以Vt为M×1阶残差向量。式（1）量测方程有解存在2种情况：M=N，且矩阵H的秩为N；M＞N，即量测系统是可观测的。由经典最小二乘估计方法求解规格化的典型负荷模式，有：

其中，Rt为t时刻M×M阶量测误差方差对角阵，起到类似权重的作用。

2 配电网表计优化配置

2.1 表计配置原则

根据配电网可观测性的分析，配置的支路量测最小表计数目为M=N，关键是找到合适的配置位置，达到以下优化目标：（1）满足式（1）中矩阵H的秩为N，即满秩；（2）量测区域之间用户负荷的功率总和应尽量保持均衡，以最大限度地保证各区域的量测对负荷的估计精度均衡，而且区域负荷的均衡对提高电压稳定性及系统安全性具有重要的意义［17］。

设某辐射状配电网络有L个节点、包含N类负荷，在L－1条支路上配置S个表计以满足上述目标，从数学上而言，这是一个组合优化问题，即在大小为CNL－1的搜索空间中找到可行解。假设网络配置S个表计后，将表计配置结果形成的量测区域视为一个子网络，则表计配置问题进一步又可转化为网络分割问题，即将网络分割为S个平均负荷功率总和尽可能均衡的子网络，在不同的子网络之间配置量测表计，得到量测矩阵H，最终的解空间就是在不同的分割方案中选择使H满秩的一组最优子网络。

2.2 表计优化配置算法

2.2.1 形成加权的深度优先搜索树

深度优先搜索DFS（Depth First Searching）算法是系统搜索一个图（G）所有节点的一种标准算法，算法的流程图如图1所示。

图1 深度优先搜索算法Fig.1 DFS algorithm

对于网络中的节点可以按2种处理方式得到它们的权重：（1）对于常规负荷用户节点i而言，其有功功率P由一段时间内负荷的耗电量求得，即P=Wd／（Dm×24），其中 Wd为耗电量，Dm为这段时间内的天数；（2）对于含DG的节点j而言，由DG一年间有功功率出力的平均值作为节点权重。

经过处理后原配电网网络就变为加权树。对于加权树首先明确以下4个概念：i=p（j）意味着节点i是节点j到根节点的路径中节点j的相邻节点，即节点i是节点j的母节点，同时节点j为节点i的子节点；没有子节点的节点称为叶节点；从节点i到根节点的路径的节点数目（不包括根节点）为节点i的长度；令T［i］表示以节点i为根节点的子树，子树总权重的定义如式（4）所示。

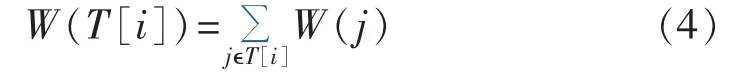
2.2.2 网络分割算法

利用网络分割算法将含有N1个节点的加权树G分为n1个连通的子集，并且使各子集的权重尽可能逼近 W（T［N1］） ／n1。 算法将沿着加权深度优先搜索生成树从叶节点到根节点的路径搜索，确定满足上述分割条件的分割点［18］。已知网络中用户负荷的分类，从每类负荷集合中任取一个节点构成算法的搜索起点集合，再从搜索起点集合中任选一组作为真正的搜索起点。若以某搜索起点为根节点的子树不包括其他搜索起点，则可以“剪化”加权树形成若干个虚拟叶节点，再继续分割。网络分割算法结合表计配置问题的物理意义须满足如下约束：

a.在网络分割过程中，所有分割形成的子网络T［j］最多包含一个搜索起点，即本文指定的每个搜索起点只能在不同的量测区域内；

b.当网络已经分割形成了n1－1个子网络，那么分割终止，因为从配电网运行需求角度考虑，馈线首端支路上一般都会配置量测表计。

网络分割算法流程图如图2所示。

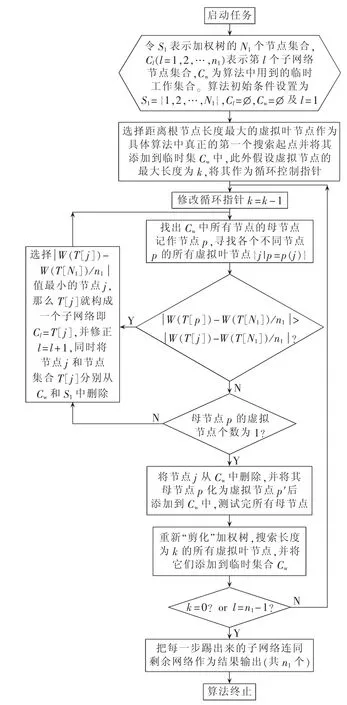
图2 网络分割算法流程图Fig.2 Flowchart of network partition algorithm

2.2.3 表计配置的优化目标

经过网络分割算法将网络加权树分割为基本均衡的子网络，并在不同子网络之间的连接支路上配置功率表计使式（1）中的矩阵H满秩，则配电网可观测。研究表明，满足上述情况的网络分割方案（即表计配置方案）不止一种，为此定义网络分割的区域均衡度指标h，如式（5）所示。h的大小即表明分割网络均衡程度的大小，h越大表明分割得出的各量测区域越均衡［18］。

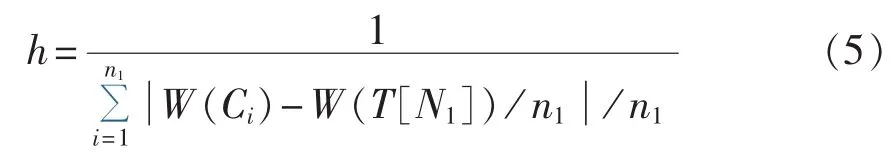
其中，W（Ci）（i=1，2，…，n1）为网络分割后各个子网络节点负荷的总权重。考虑到DG出力受环境等因素的影响具有随机性和不确定性，则含DG节点的子网络的权重随之变化，这将导致式（5）所示区域均衡度指标变化，所以在考虑表计配置优化目标时需要计及DG出力的不确定性。

此外，网络在实际运行中可能已经配置一定数量的功率表计，所以为了减小量测系统中表计配置的总数量，表计的布点位置应尽可能与已有的表计布点位置重合，以减少新表计的添加，达到降低经济耗费的目标。因此，为了确定最优的表计配置方案，需要考虑以下优化目标。

（1）计及网络中已有的功率表计，整个网络中总的测量表计数目f取满足网络可观测性前提下的最小值，即：

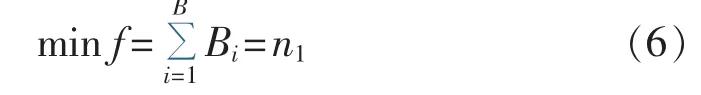
其中，Bi（Bi∈｛0，1｝；i=1，2，…，B）表示支路是否布置功率表计，Bi=1表示该支路布置功率表计，Bi=0表示该支路没有布置功率表计；B为配电网中的支路数。由于配电网馈线首端支路上一般都会配置量测表计，所以B1=1。结合前文配电网可观测性的分析，f的取值为［n1，n1+b］范围内的整数，b 为网络中原有的表计数量。

（2）计及DG出力的不确定性，保证量测区域均衡度指标h的取值应尽可能地大，即：

根据上述优化目标，对满足网络可观测性的表计配置方案进行优化选择，输出最优表计配置方案。表计优化配置算法流程图如图3所示。

3 DG出力不确定性的处理

3.1 风力发电机有功出力概率分布

对风速的大量实际测量数据表明，绝大多数地区的年平均风速分布都符合Weibull分布［19］，则风速的概率密度函数可由下式描述：

其中，v为风速；K、c以及v0为Weibull分布的3个参数，K为形状参数，c为尺度参数，v0为位置参数。

根据风速的分布与风力发电机风速-功率曲线推导出风力发电机的有功功率分布的解析表达式Fpwtg（P）。风力发电机风速-功率曲线可描述为：

其中，vci为切入风速；vN为额定风速；vco为切出风速；PN为风力发电机的额定功率。

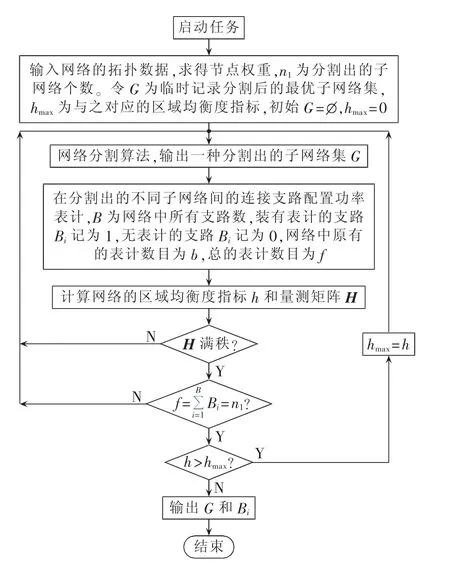
图3 表计优化配置算法流程图Fig.3 Flowchart of meter allocation optimization algorithm

设Pwtg为风力发电机有功功率随机变量，F（v）为轮毂高度处风速的分布函数。则有：

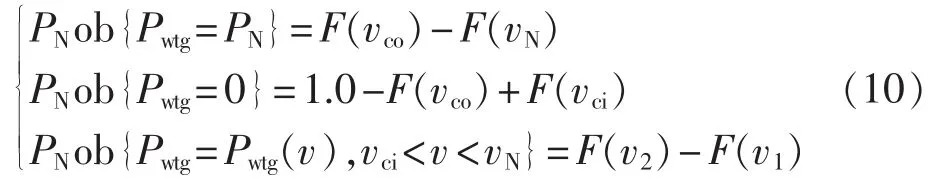
其中，ob｛·｝表示风力发电机的目标发电功率；v1为风轮前来流速度；v2为风轮后尾流速度。

利用式（9）可以求出风力发电机有功功率分布Fpwtg（P）。

3.2 光伏电站有功出力概率分布

光伏发电系统的输出功率与光照强度密切相关，由于光强具有随机性，因此光伏发电的输出功率也是随机的。据统计，在一定时间段（1小时或几小时）内，太阳光照强度可以近似看作 Beta分布［19］，其概率密度函数为：

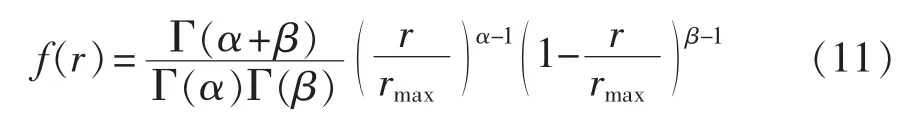
其中，r和rmax分别为实际光强和最大光强；α、β均为Beta分布的形状参数；Γ为Gamma函数。由在一定时间段内的光照强度平均值u和方差σ2可以得到光强Beta分布的参数如式（12）、（13）所示。

根据光照强度、光照面积及光电转换效率，光伏发电系统的有功出力概率密度分布可以表示为：

其中，Pmax为光伏发电系统最大输出有功功率；Pt=rAη为t时刻光伏发电系统的实际输出功率，A为光照总面积，η为光电转换效率。

3.3 拉丁超立方抽样

在基于网络分割的表计优化配置中，DG节点的有功出力会影响网络分割的区域均衡度指标，为了计及DG出力的不确定性，引入拉丁超立方抽样方法，该方法可以使抽样点尽可能覆盖整个分布区间，采样稳健性好，可以有效克服截尾现象，从而提高抽样精度和效率［20］。运用此方法对DG的出力概率分布函数进行抽样，使采样值尽可能覆盖DG出力的波动范围。假设任意一随机变量XK，其累计概率分布函数为：

设N2为采样规模，则拉丁超立方抽样方法为：将分布函数曲线的纵轴分成N2个等间距但是不重叠的区间（由于 YK∈［0，1］，则每一个区间的长度为1／N2），选择每一个区间的中点作为YK的采样值，然后用函数的反函数来计算XK的采样值，即XK的第q个采样值如式（16）所示。拉丁超立方抽样示意图如图4所示。

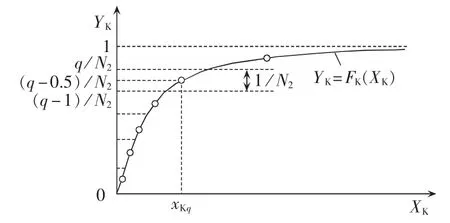
图4 拉丁超立方抽样示意图Fig.4 Schematic diagram of Latin hypercube sampling

4 算例分析

针对文献［21］中的14节点实际配电网络及IEEE 33节点配电网络系统进行改造作为算例网络。14节点配电网络中，在节点5、7、10、12处接入风力发电机，用户负荷分为4类，包括3类常规负荷和1类风力发电负荷；IEEE 33节点系统中，在节点3、7、12处接入风力发电机，节点14、24、28处接入光伏发电站，则系统含有5类常规负荷、1类风力发电负荷和1类光伏发电负荷。2个测试系统的用户类型信息见表1。

图5和图6分别为14节点配电网络和IEEE 33节点系统添加DG节点后的期望网络结构的加权树，假设网络中已有的表计布点位置如图中标注［21］。图中，1（81.4）表示节点编号为1、节点功率权重为81.4，其他类似；WTG（100）、WTG（200）表示风力发电机，PV（100）、PV（200）表示光伏发电站，括号中的数值为额定容量（单位为kW），假设相同额定容量的同类DG具有相同的有功出力分布规律，且同一配电网络中同类DG发出功率的变化趋势一致，各DG出力分布参数见表2。根据各DG出力分布参数得到其年有功功率的出力分布及概率分布函数，在不计及DG出力不确定性的情况下，求取各DG出力的年平均值：WTG（100）为 42.6 kW，WTG（200）为 95.3 kW，PV（100）为 25.4 kW，PV（200）为 45.5 kW，加权树中DG节点的权重取其负值。对于14节点配电网络，网络总权重为981.6，划分的量测区域等于负荷分类数4，且每个量测区域的权重应接近981.6／4=245.4。同理，对于IEEE33节点系统划分的量测区域数为7，每个量测区域的权重应接近3385.5／7≈483.643。运用2.2节中的表计优化配置算法得到2个测试系统的最优表计配置，配置结果见表3。

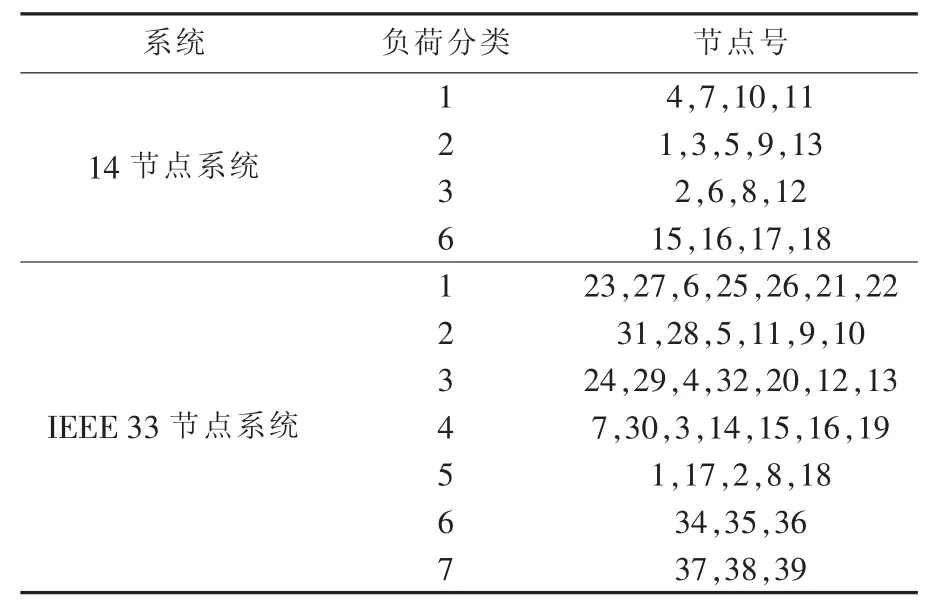
表1 各节点用户类型信息Table 1 Load type of nodes

图5 14节点配电网络添加DG节点后的加权树Fig.5 Weighting tree of 14-bus distribution network with DG nodes

图6 IEEE 33节点配电网络添加DG节点后的加权树Fig.6 Weighting tree of IEEE 33-bus distribution network with DG nodes

表2 各DG相关性能参数Table 2 Related performance parameters of DGs

表3 最优表计配置结果Table 3 Optimized meter allocation scheme

由表3的表计配置结果可得结论如下。

（1）对于14节点配电网络，在满足网络可观测性的前提下，网络中总的表计配置数目为最小值f=4，且量测区域的区域均衡度指标h=0.0205，大于其他配置的区域均衡度指标，满足了表计优化配置的条件；同理，对于IEEE 33节点系统，最优表计的分布位置最大限度地与原有的表计布点位置重合，保证了表计总数目最少f=7，且区域均衡度指标h=0.0082，大于其他配置的区域均衡度指标，实现了表计配置的最优化。

（2）综合2个测试系统的配置结果可以看出，DG接入配电网后，表计的配置位置多分布在靠近DG接入点处，DG作为一种“负”的负荷，其引入可以平衡周围节点用户负荷的功率，所以DG出力的大小会影响网络的分割，表计配置及各量测区域的均衡度也会改变。

由于DG出力的随机性和不确定性，当DG出力较年平均功率有较大波动时，表3中的表计配置方案可能不再满足优化目标，故需要计及DG出力的不确定性做进一步研究。

运用拉丁超立方抽样技术对各DG的功率概率分布进行抽样，抽样规模取N2=1000，其中第s个样本值记为Ns。将这1000个样本值作为各DG节点的注入功率，进行了1000次表计优化配置算法的模拟实验，得出在DG有功出力波动情况下的最优表计配置方案，配置结果见表4。

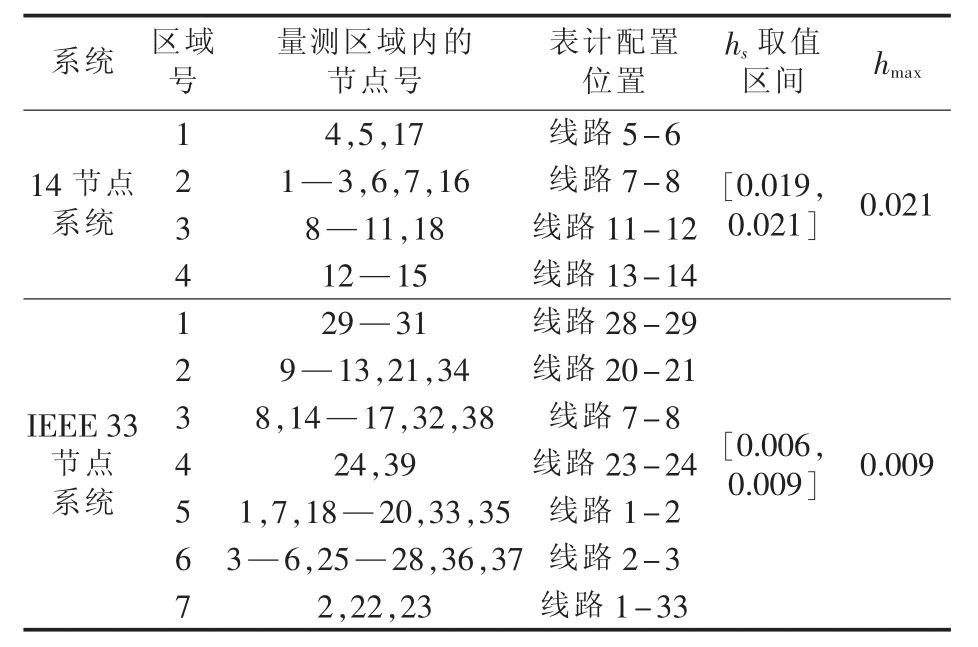
表4 考虑DGs不确定性的最优表计配置结果Table 4 Optimized meter allocation scheme considering DGs uncertainty

比较表3和表4中的配置结果可得结论如下。

（1）对于14节点配电网络，计及DG出力不确定性时的最优表计配置与不考虑DG出力波动时相同。表3的配置结果中各量测区域权重相近，且每个量测区域中均包含一个风力发电机节点，在假设各风力发电机节点出力变化一致时，各量测区域的权重也同步变化，所以在DG出力波动时该配置方案仍满足均衡度的要求。

（2）对于IEEE 33节点系统，在表3配置方案下，各量测区域的权重相差略大，且DG节点在各量测区域中的分布也不均匀，故当考虑DG出力波动时，量测区域的权重会存在更大的差别，这将不再满足负荷均衡度的最大化，所以计及DG不确定性时，得到了表4中不同于表3的最优配置方案。该配置方案满足了系统可观测性，实现了经济耗费的最小化，且在DG出力波动时保证了区域均衡度指标的最大化，任意一个样本值Ns所对应的区域均衡度指标hs都趋近最大区域均衡度指标hmax。

5 结论

本文结合DG接入后配电网的特点，提出了一种基于可观测性分析的计及DG出力不确定性的配电网表计优化配置算法。在14节点配电网络系统和IEEE 33节点系统上进行了测试计算，验证了算法的有效性，得到了在保证网络可观测性前提下计及DG出力不确定性的最优表计配置方案。该方案实现了网络经济耗费的最小化，且在DG出力波动的情况下，满足了量测区域负荷均衡度指标的最大化。

在研究过程中发现，表计配置算法在实际运行中，除了要考虑本文提出的与已有的表计布点位置尽可能重合的条件外，还需考虑以下2点。

（1）表计发生故障可能使网络不可观测，此时可以通过增加负荷伪量测作为故障表计量测的补充，从而保持网络的可观测性。

（2）从规划角度考虑，用期望网络结构解决可观测性和表计配置问题是一个简单、有效的解决办法，但配电网网络结构的变化存在随机性，按期望网络结构得到的表计配置方案不一定总能使网络可观测。对此，表计可以配置在期望网络结构的联络开关处，以降低网络结构变化时的不可观测概率；或者也可以通过补充伪量测来解决可观测性问题。

参考文献：

［1］MONTENEGRO D，RAMOS G A.Real time observability analysis for distribution networks［C］∥2013 IEEE Grenoble Conference.Grenoble，France：IEEE，2013：1-5.

［2］CASTILLO E，CONEJO A J，PRUNEDA R E，et al.State estimation observability based on the null space of the measurement Jacobian matrix［J］.IEEE Transactions on Power Systems，2005，20（3）：1656-1658.

［3］DO COUTTO FILHO M B，DE SOUZA J C S，TAFUR J E V.Quantifying observability in state estimation［J］.IEEE Transactions on Power Systems，2013，28（3）：2897-2906.

［4］POWALKO M，ORTHS A G，ABILDGAARD H，etal.System observability indices for optimal placement of PMU measurements［C］∥2012 IEEE Power and Energy Society General Meeting.San Diego，CA，USA：IEEE，2012：1-6.

［5］COSTA A S，LOURENCO E M，CLEMENTS K A.Power system topological observability analysis including switching branches［J］.IEEE Transactions on Power Systems，2002，17（2）：250-256.

［6］SCHLOSSER T，ANGIONI A，PONCI F，et al.Impact of pseudomeasurements from new load profiles on state estimation in distribution grids［C］∥Instrumentation and Measurement Technology Conference （I2MTC）.Montevideo，Uruguay：IEEE，2014：625-630.

［7］ANGIONI A，SCHLOSSER T PONCI F，et al.Impact of pseudomeasurements from new load profiles on state estimation in lowvoltage grids［J］.IEEE Transactions on Instrument and Measurement，2016，65（1）：70-77.

［8］林君豪，张焰，陈思，等.考虑可控负荷影响的主动配电系统分布式电源优化配置［J］. 电力自动化设备，2016，36（9）：46-53.LIN Junhao，ZHANG Yan，CHEN Si，et al．Optimal DG allocation considering effect of controllable load for active distribution system［J］.Electric Power Automation Equipment，2016，36（9）：46-53.

［9］卫志农，陈胜，孙国强，等．含多类型分布式电源的主动配电网分布式三相状态估计［J］. 电力系统自动化，2015，39（9）：68-74.WEIZhinong，CHEN Sheng，SUN Guoqiang，etal.Distributed three-phase state estimation for active distribution network integrated with differenttypes ofdistributed generators ［J］.Automation of Electric Power Systems，2015，39（9）：68-74.

［10］HAUGHTON D A，HEYDT G T.A linear state estimation formulation for smart distribution systems［J］.IEEE Transactions on Power Systems，2013，28（2）：1187-1195．

［11］SHAFIU A，JENKINS N，STRBAC G.Measurement location for state estimation of distribution networks with generation［J］.IEE Proceedings-Generation，Transmission and Distribution，2005，152（2）：240-246.

［12］HAUGHTON D A，HEYDT G.A linear state estimation formulation for smart distribution systems［J］.IEEE Transactions on Power Systems，2013，28（2）：1187-1195.

［13］LIU J Q，PONCI F，MONTI A，et al.Optimal meter placement for robust measurement systems in active distribution grids［J］.IEEE Transactions on Instrumentation and Measurement，2014，63（5）：1096-1105.

［14］CHEN C S，HWANG J C，HUANG C W.Application of load survey systems to proper tariff design［J］.IEEE Transactions on Power Systems，1997，12（4）：1746-1751.

［15］JARDINI J A，TAHAN C M V，GOUVEA M R，et al.Daily load profiles forresidential，commercialand industriallow voltage consumers［J］.IEEE Transactions on Power Delivery，2000，15（1）：375-380.

［16］王薪苹，卫志农，孙国强，等.计及分布式电源和负荷不确定性的多目标配网重构［J］. 电力自动化设备，2016，36（6）：116-121.WANG Xinping，WEIZhinong，SUN Guoqiang，etal.Multiobjective distribution network reconfiguration considering uncertainties of distributed generation and load［J］.Electric Power Automation Equipment，2016，36（6）：116-121.

［17］随慧斌，赵建国，李可军，等.考虑不均衡区域负荷增长的在线电压稳定评估［J］. 电力自动化设备，2011，31（3）：57-61.SUI Huibin，ZHAO Jianguo，LI Kejun，et al.On-linevoltage stability assessment considering uneven growth of regional load［J］.Electric Power Automation Equipment，2011，31（3）：57-61.

［18］毕天姝，焦连伟，严正，等．用于分布式故障诊断系统的新型网络分割法［J］. 电力系统自动化，2001，25（16）：16-21．BI Tianshu，JIAO Lianwei，YAN Zheng，et al.Graph partitioning method for distributed fault section estimation system in power networks［J］．Automation of Electric Power Systems，2001，25（16）：16-21.

［19］周竞，王珂，石飞，等.计及源荷双侧响应的概率潮流计算方法［J］. 电力自动化设备，2016，36（8）：76-81，89.ZHOU Jing，WANG Ke，SHI Fei，et al.Probabilistic power flow algorithm considering source-side and load-side responses［J］．Electric Power Automation Equipment，2016，36（8）：76-81，89.

［20］江知翰，陈金富.计及不确定性和多投资主体需求指标的分布式电源优化配置方法研究［J］.中国电机工程学报，2013，33（31）：34-42.JIANG Zhihan，CHEN Jinfu.Study on optimaldistributed generator allocation method considering uncertainties and requirements of different investment entities［J］.Proceedings of the CSEE，2013，33（31）：34-42.

［21］陈得治，郭志忠.基于表计配置的配电网可观测性分析［J］.中国电机工程学报，2005，25（12）：35-41.CHEN Dezhi，GUO Zhizhong.Distribution system network observability analysis based on meter placement［J］.Proceedings of the CSEE，2005，25（12）：35-41.