犬骨型核石墨四点弯曲实验与模拟

顾晨光 曾广礼 杨雄 钟阳 丁冬



犬骨型核石墨四点弯曲实验与模拟

顾晨光1,2曾广礼1杨雄1,2钟阳1,2丁冬1,2

1（中国科学院上海应用物理研究所嘉定园区 上海 201800） 2（中国科学院大学 北京 100049）

核石墨是熔盐堆的关键材料之一，断裂性能是核石墨的重要属性之一。首先通过四点弯曲实验测量了犬骨型核石墨的断裂载荷，观察裂纹扩展路径再运用扩展有限单元法(Extended finite element method, XFEM)对这一实验过程进行了模拟。模拟得到的裂纹扩展路径和断裂实验结果有很好的一致性，证明利用XFEM可以准确地模拟核石墨的断裂过程。同时确定了适用于核石墨的断裂准则。

核石墨，断裂载荷，扩展有限单元法，数值模拟

核石墨是耐高温材料，有较好的抗辐照性能，具有较高的中子散射截面和极低的热中子吸收截面，在反应堆中用作中子慢化剂、反射层和结构材料[1]。服役中的核石墨由于长时间遭受快中子辐射，其结构的完整性会受到破坏，从而影响材料性能使组件失效[2]。基于此，对核石墨特性进行理论分析和实验测试是有必要的。为抵消反应堆寿期内因热和中子辐照引起的变形，核石墨构件主要设计成石墨砖的形式。温度梯度和中子通量梯度导致的尺寸改变将使石墨砖内部产生应力集中，甚至足以在砖键槽角落和不连续的地方产生裂纹起裂点。此外，石墨砖是反应堆堆芯中不可替换的组件，其结构完整性直接影响反应堆的使用寿命，因此有必要对核石墨进行断裂力学分析。

1999年，美国西北大学的Belytschko研究组[3]提出了一种处理间断问题的新计算方法，即采用最小重构网格的有限元方法来模拟弹性裂纹的扩展。2000年，Daux等[4]引入连续函数考虑多分支裂纹，并正式将该方法命名为扩展有限单元法(Extended finite element method, XFEM)。XFEM是基于单位分解的思想引入带有不连续性质的扩充形函数来代表间断，无需重新划分网格。由于XFEM在继承了标准有限单元法优势的同时还能有效处理不连续性问题，因此近年来该方法在固体力学[5‒6]、流体力学[7‒8]等不连续问题上得到了广泛应用。国际上在裂纹应用方面，研究人员利用扩展有限单元法开展了很多相关工作。例如，Sukumar等[9]曾对三维平面I型裂纹问题进行了研究；Areias等[10]运用四面体单元的扩展有限单元法分析了三维裂纹的起裂和扩展；Gasser等[11]在三维条件下对混凝土裂纹扩展的情况进行了模拟；Ferrié等[12]模拟了Al-Li合金中半椭圆裂纹的疲劳开裂，利用三维裂纹扩展准则考虑沿裂纹波前闭合应力的线性变化，其数值模拟结果和实验获得的疲劳裂纹相吻合。

在核石墨方面的应用，王莞珏等[13]使用基于内聚力模型的扩展有限单元法对单边切口梁的三点弯曲试验进行数值模拟来研究IG-11核石墨断裂韧性的尺寸效应，其模拟结果与文献[14]中的实验结果吻合得很好。所以通过建立合适的有限元模型可以分析核石墨材料的断裂特性，为实验提供理论指导的同时，可以有效减少实验的经费和时间。

因此，首先通过四点弯曲实验方法测量熔盐堆用细颗粒核石墨的断裂载荷，然后利用XFEM方法对上述实验过程进行模拟，并将模拟得到的裂纹扩展路径和断裂载荷与实验结果进行对比，目的是建立能模拟核石墨断裂过程的模型，为今后的研究打下数值模拟的基础。

1 四点弯曲实验

本实验中采用首款熔盐堆专用的细颗粒核石墨NG-CT-10样品。该型号核石墨拥有优秀的力学、热学性能、良好的纯度和均一性，防熔盐浸渗性能优于进口核石墨[15]。样品尺寸为350 mm()× 60mm()×80 mm()，如图1所示。分别有4种不同倒角半径为0 mm（即无倒角）、1 mm、5 mm、10 mm的核石墨，每种核石墨共11个样品，总计44个样品。

实验装置如图2所示，依据实验要求，上下夹具的跨距分别设为100 mm和300 mm。设定美特斯MTS万能试验机的上夹具，以位移的模式向核石墨加载进行四点弯曲实验直至核石墨断裂，然后测量断裂载荷。

四点弯曲实验测量得到的断裂载荷结果如表1所示。表1中数据显示，对于犬骨型核石墨，随倒角半径的增加断裂载荷也增加。该现象说明有较大倒角半径的核石墨抗弯能力更好。从标准差可以判断实验数据有着较好的一致性，其结果具有一定的可靠性。

图1 样品尺寸（以R=5 mm为例）

图2 实验装置

表1 不同倒角半径R的核石墨断裂载荷实验结果

图3是4种不同倒角半径核石墨的断裂结果。结果显示，所有的样品都只产生了一条裂纹，并且裂纹都是从倒角处起裂，说明无论是直角还是圆角，在倒角处都存在着应力集中的现象。结合表1，断裂载荷的增加幅度随着倒角半径的增加在减小，倒角半径的增加能明显缓解倒角处的应力集中。裂纹起裂后以一定的弧度呈弧线扩展，在临近上边界时出现拐点而改变裂纹的扩展方向，这在=5 mm和=10 mm的核石墨中特别明显。但是由于样品具有对称性，裂纹的起裂位置出现在左边还是右边具有随机性。

此外，断裂载荷在倒角半径=0 mm（即直角）时有一最小值，说明在该条件下应力集中现象最严重，导致核石墨在较小的载荷下就发生了断裂，实际应用中应避免这种设计。

图3 不同倒角半径R的核石墨断裂结果 (a) R=0 mm，(b) R=1 mm，(c) R=5 mm，(d) R=10 mm

2 数值模拟

2.1 XFEM方法的数值模拟原理

由于基于XFEM粘性片段法的定律与在控制粘性单元中考虑牵引分离本构行为的定律相似，也适合于脆性材料的裂纹扩展问题。因此本文采用有限元软件ABAQUS的XFEM[16]方法进行裂纹扩展模拟。该方法主要由损伤初始准则和损伤演化定律组成。

2.1.1 损伤初始准则

由于实验中比较容易测得应力，因此通常采用应力相关准则。

1) 最大主应力准则：

2) 最大正应力准则：

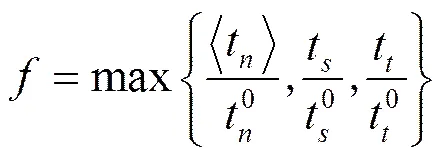
式中：<t>为垂直于可能出现的裂纹面的应力分量；t、t为两个可能出现的裂纹面上的切向分量。可能出现的裂纹面垂直于局部坐标轴1或2。

3) 二次牵引影响准则：

在模拟时，可以选用任意准则。通常当断裂准则中计算的超过1.0后，在一个增量步后将会引进新的裂纹或是扩展已经存在的裂纹长度。

2.1.2 损伤演化定律

XFEM的损伤演化定律有两种：线性损伤演化定律和指数损伤演化定律。由于研究对象NG-CT-10核石墨是一种脆性材料，可以确定在模拟中将采用线性损伤演化定律。

2.2 数值模型与模拟结果

依据实验中使用的核石墨样品尺寸，并对实验夹具进行简化，建立如图4所示的数值模型。

图4 数值模型（以R=5 mm为例）

在模拟中，核石墨样品和夹具的材料参数取值如表2所示。

表2 ABAQUS模拟相关材料参数

首先将分别针对上文中三个准则进行模拟，然后通过和实验结果对比，确定核石墨适用于哪些准则。先建立=0 mm的模型，在模型底部相距300mm的位置施加位移约束来模拟实验中的下跨距，在上方相距100 mm的夹具上施加位移载荷模拟加载过程。

图5(a)是最大主应力准则模拟结果，为了更好与实验结果对比，模拟结果是以未变形的图展示。从图5(a)可以看到，裂纹的起裂点在直角附近，扩展呈弧线型，这和实验观察到的现象一致。而图5(b)和(c)分别是最大正应力准则和二次牵引准则模拟结果，虽然两者的裂纹起裂点也在直角附近，但裂纹的扩展方向呈直线型。这与实验所获得的结果完全不同，说明这两个裂纹扩展准则不适用于核石墨的裂纹扩展模拟。综合三个准则的模拟结果，最终确定最大主应力准则适用于核石墨断裂的模拟。

图5 最大主应力(a)、最大正应力(b)、二次牵引(c)准则模拟结果

选定最大主应力准则作为核石墨断裂的模拟标准之后，结合实验，分别建立倒角半径=0 mm、1mm、5 mm、10 mm的模型，最大主应力取表2中NG-CT-10核石墨的抗弯强度。同样，在样品底部相距300 mm的位置施加位移约束来模拟实验中下跨距，在上方相距100 mm的夹具上施加位移载荷模拟加载过程。模拟结果如图6所示。

首先直观地对比模拟和实验得到的裂纹扩展路径，可以看到：

1) 由于模型和实验一样，样品是完整对称的，所以裂纹从样品的左边还是右边起裂不确定，但是结果都只产生一条裂纹。

2) 对于4种倒角半径的模型，无论裂纹是从左边还是从右边起裂，裂纹的起裂点都在倒角的边缘上，这与实验观察到的现象一致。

3) 对于4种倒角半径的模型，起裂以后裂纹扩展路径都以弧线的轨迹进行扩展，直至整个扩展过程的约2/3处，在该处出现了一个拐点，裂纹扩展方向有所改变，这在实验结果图3(c)和(d)可以明显观察到。并且以此为分界点，该分界点的存在根据所选用的断裂准则可以判断是由于最大主应力方向的变化引起。

4) 裂纹前段部分和实验结果十分接近。分界点之后，模拟结果和实验结果有些分歧：在=0 mm、1mm时，实验中裂纹扩展曲线没有明显的分界点，而模拟中则较为明显；在=5 mm、10 mm时，实验和模拟都有明显的分界点。然而模拟结果中，=5mm时裂纹呈现直线，=10 mm时裂纹呈现S型。这些差异主要是由于网格划分、XFEM方法本身存在局限性引起，但是考虑到数值计算本身存在着误差，这些差异是在可以接受的范围内。

通过模拟得到的断裂载荷如表3所示（表中误差负号表示断裂载荷模拟值小于实验值）。由于数值模拟计算都是以应力作为计算结果，因此为了获得能和实验相对应的载荷，在输出结果中同时也输出了夹具与样品的接触面积，从而得到模拟断裂载荷。对比实验和模拟的断裂载荷，两者结果十分接近，误差在5%左右。考虑到数值计算本身存在误差，而且由于ABAQUS XFEM本身只支持一阶单元，计算精度会有所局限等原因，可以认为模拟结果和实验结果是一致的。

至此，通过对模拟得到的裂纹扩展路径和断裂载荷的分析以及和实验的对比，可以证明利用XFEM可以较准确地模拟核石墨的断裂过程。

图6 R=0 mm (a)、1 mm (b)、5 mm (c)、10 mm (d)模拟结果

表3 数值模拟结果

3 结语

通过四点弯曲实验方法测量NG-CT-10核石墨的断裂载荷，获得了该形状核石墨的裂纹扩展路径。实验结果表明，对这种形状的核石墨，断裂载荷随着倒角半径而增加。这种现象说明在=0‒10mm的范围内，倒角半径越大，核石墨的抗弯能力越好。断裂载荷在倒角半径=0 mm有一最小值，在该条件下应力集中现象最严重，实际应用中应避免这种设计。

在数值模拟方面，利用XFEM成功实现了对这一实验过程的数值模拟。首先确定了适用于核石墨的断裂准则——最大主应力准则，然后在该基础上利用XFEM对不同倒角半径的核石墨进行模拟，准确地获取了裂纹的起裂点和扩展路径，并且比较准确地获取断裂载荷，误差在5%左右，证明XFEM可以用于核石墨断裂过程的模拟，为今后复杂或难以实现的实验打下数值模拟的基础。

1 Li Z, Chen D, Fu X,. The influence of pores on irradiation property of selected nuclear graphites[J]. Advances in Materials Science and Engineering, 2012, (3): 640462. DOI: 10.1155/2012/640462.

2 Wang P, Contescu C I, Yu S,. Pore structure development in oxidized IG-110 nuclear graphite[J]. Journal of Nuclear Materials, 2012, 430(1): 229‒238. DOI: 10.1016/j.jnucmat.2012.07.015.

4 Daux C, Moës N, Dolbow J,. Arbitrary branched and intersecting cracks with the extended finite element method[J]. International Journal for Numerical Methods in Engineering, 2000, 48(12): 1741‒1760. DOI: 10.1002/ 1097-0207(20000830)48:12<1741::AID-NME956>3.0.CO;2-L.

5 Chessa J, Smolinski P, Belytschko T. The extended finite element method (XFEM) for solidification problems[J]. International Journal for Numerical Methods in Engineering, 2002, 53(8): 1959‒1977. DOI: 10.1002/ nme.386.

6 Merle R, Dolbow J. Solving thermal and phase change problems with the extended finite element method[J]. Computational Mechanics, 2002, 28(5): 339‒350. DOI: 10.1007/s00466-002-0298-y.

7 Wagner G J, Moës N, Liu W K,. The extended finite element method for rigid particles in Stokes flow[J]. International Journal for Numerical Methods in Engineering, 2001, 51(3): 293‒313. DOI: 10.1002/nme. 169.

8 Chessa J, Belytschko T. An extended finite element method for two-phase fluids[J]. Journal of Applied Mechanics, 2003, 70(1): 10‒17. DOI: 10.1115/1.1526599.

9 Sukumar N, Moës N, Moran B,. Extended finite element method for three-dimensional crack modelling[J]. International Journal for Numerical Methods in Engineering, 2000, 48(11): 1549‒1570. DOI: 10.1002/ 1097-0207(20000820)48:11<1549::AID-NME955>3.0.CO;2-A.

10 Areias P, Belytschko T. Analysis of three-dimensional crack initiation and propagation using the extended finite element method[J]. International Journal for Numerical Methods in Engineering, 2005, 63(5): 760‒788. DOI: 10.1002/nme.1305.

11 Gasser T C, Holzapfel G A. Modeling 3D crack propagation in unreinforced concrete using PUFEM[J]. Computer Methods in Applied Mechanics and Engineering, 2005, 194(25): 2859‒2896. DOI: 10.1016/ j.cma.2004.07.025.

Analysis of Spatial Structure of Water Tourism Scenic Spots in Arid and Semi-arid Areas——A Case Study of Xinjiang____________________________XIN Long,Wahap·Halik,ZHU Yongfeng 30

12 Ferrié E, Buffière J Y, Ludwig W,. Fatigue crack propagation:visualization using X-ray microtomography and 3D simulation using the extended finite element method[J]. Acta Materialia, 2006, 54(4): 1111‒1122. DOI: 10.1016/j.actamat.2005.10.053.

13 王莞珏, 史力, 赖士刚, 等. IG-11石墨材料断裂韧性数值模拟研究[J]. 原子能科学技术, 2014, 48(10): 1857‒1861. DOI: 10.7538/yzk.2014.48.10.1857. WANG Wanjue, SHI Li, LAI Shigang,. Numerical simulation of fracture toughness on nuclear graphite IG-11[J]. Atomic Energy Science and Technology, 2014, 48(10): 1857‒1861. DOI: 10.7538/yzk.2014.48.10.1857.

14 史力, 王洪涛, 王海涛,等. 核级石墨材料断裂韧性实验研究[J]. 核动力工程, 2011, (S1): 185−188 SHI Li, WANG Hongtao, WANG Haitao,. Experimental study on fracture toughness of nuclear graphite[J]. Nuclear Power Engineering, 2011, (S1): 185−188.

15 蔡翔舟, 戴志敏, 徐洪杰. 钍基熔盐堆核能系统[J]. 物理, 2016, 45(9): 578‒590. DOI: 10.7693/wl20160904. CAI Xiangzhou, DAI Zhimin, XU Hongjie. Thorium molten salt reactor nuclear energy system[J]. Physics, 2016, 45(9): 578‒590. DOI: 10.7693/wl20160904.

16 Systèmes D. ABAQUS analysis user’s manual[Z]. Abaqus, Providence, RI, 2012.

Four-point bending experiment and simulation of dog bone nuclear graphite

GU Chenguang1,2ZENG Guangli1YANG Xiong1,2ZHONG Yang1,2DING Dong1,2

1(Shanghai Institute of Applied Physics, Chinese Academy of Sciences, Jiading Campus, Shanghai 201800, China) 2(University of Chinese Academy of Sciences, Beijing 100049, China)

Background: Nuclear graphite is a key material in Molten Salt Reactor (MSR). And fracture property is one of the most important parameters of the nuclear graphite. Purpose: This study aims at the failure stress of the graphite and to develop a numerical model to simulate the experiment. Methods: The four-point bending test was employed to find the failure stress of the dog bone graphite. And a numerical model has been developed for simulation by using the extended finite element method (XFEM). Results: The failure stress of NG-CT-10 dog bone nuclear graphite has been investigated through the four-point bending test, and the experiment results are in accord with the numerical simulation results. Conclusion: The numerical model in XFEM can accurately simulate the fracture process of the nuclear graphite, and the fracture criterion can be determined accordingly for nuclear graphite.

Nuclear graphite, Failure stress, XFEM, Numerical simulation

TL99

10.11889/j.0253-3219.2017.hjs.40.050601

顾晨光，男，1991年出生，2014年毕业于南京航空航天大学，现为硕士研究生，研究领域为核石墨断裂力学

曾广礼，E-mail: zengguangli@sinap.ac.cn

2017-01-10，

2017-02-14

Supported by Ministry of Harman Resources and Social Security of People’s Republic of China (No.Y419016031)

中华人民共和国人力资源和社会保障部应用课题(No.Y419016031)资助

GU Chenguang, male, born in 1991, graduated from Nanjing University of Aeronautics and Astronautics in 2014, master student, focusing onnuclear graphite fracture mechanics

ZENG Guangli, E-mail: zengguangli@sinap.ac.cn

2017-01-10, accepted date: 2017-02-14