一堂有趣的迷宫课
2017-05-20潘德慧
潘德慧
引子
1.经常看见学生玩走迷宫的游戏,这个内容是学生很熟悉、很喜欢的。走迷宫既是趣味数学又是游戏,可以使任何水平的学生都从自己的最佳观测点面对每一个题材。学生除了学到数学的内容,体验数学的思维方式,还可以培养正确的学习态度。
2.一般人看迷宫是眼花缭乱,但对数学家来说,一座迷宫只是一个拓扑学问题。拓扑学是研究连续性现象的数学分支,也是渗透于整个现代数学的思想方法。笔者希望通过这个课例稍作渗透,给学生埋下一颗智慧的种子。多年后,他接触到拓扑学时,可能会隐约记得,曾经在走迷宫时就运用过这个知识。
于是,笔者决定上一堂有趣的迷宫课。
教学过程
一、初步感知迷宫。
师:同学们,今天的课,潘老师要和大家开始一段奇妙的旅行!想去吗?出发吧!(课件演示世界上各种著名的实体迷宫)你们看到了什么?
二、迷宫的含义及来历。
师:你知道什么是迷宫吗?(揭示:迷宫是一种锻炼人类智慧的游戏。)
1.关于迷宫的传说。(课件演示)
師:迷宫之所以吸引人,在于它的趣味性及对智力的挑战性。但迷宫产生之初可不是一种玩具,这是传说中最早修建的迷宫———米洛斯王宫,这里还流传着一个神话故事。在古希腊,有一个国王叫米诺斯,他答应送给海神礼物,却说话不算数。海神生气了,给他的王后下了咒语。王后生下了一个牛脑袋、人身体的怪物。这对王室来说是个很大的丑闻。所以,国王命令岛上最优秀的工匠造了一座迷宫,把怪物关在里面,让它永远不能离开。这座迷宫非常复杂,连造它的工匠进去以后也找不到出来的路。这个怪物整天在迷宫里游荡,吃的是雅典进贡的童男童女。雅典王子为了拯救雅典的孩子们,拿着宝剑和线团闯进了迷宫。他一路走一路退下线团,找到了怪物,杀死了它,又沿着这根线找到出口,活着离开了迷宫。
2.概括迷宫的含义。
师:迷宫最早是对结构复杂、道路难辨,进去后不容易找到出口的建筑物的总称。后来,就演变成了一种深受大家喜欢的智力游戏。
三、迷宫的结构。
1.介绍迷宫。
迷宫中的黑线代表着墙壁,空白代表着通道。2.迷宫为什么很难找到出口?
①从起点开始,从终点走出去。
②路线复杂。(有走不通的死路、有几条路的岔路、走得通的通路)
四、走迷宫的方法。
(一)怎样走出单联通迷宫?
1.学生尝试走纸上迷宫。
师:介绍了这么多,相信大家已经跃跃欲试了!那就开始游戏吧!看这个迷宫(如图),从左上角的起点开始,从右下角的终点走出。看谁能走出来。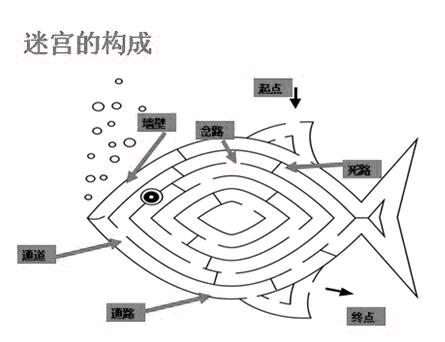
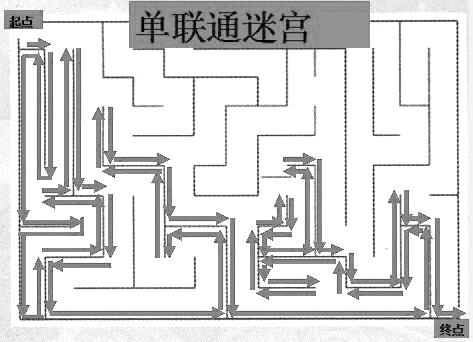
2.介绍单联通迷宫。
师:简单吗?
生:简单,我很快就走出来了。
师:如果你是置身于一个真正的迷宫中,不知道终点在哪里,怎样才能走出这个迷宫呢?我们一起观察这个迷宫的特点。
小结:像这样从起点到终点之间的墙都是连着的迷宫,叫做单联通迷宫。
3.介绍单手法则。
师:单联通迷宫走起来比较简单,只要你用左手(或者右手)摸着墙,沿着迷宫中的一面墙,一直往前走,就能到达目的地。这种方法叫单手法则。用单手法则虽然不能保证走的是最短的路线,但能让你在迷宫中不迷路,顺利走出来。
(二)复杂的迷宫(多联通迷宫)。
1.介绍多联通迷宫。
①介绍回路。
师:这样一个简单的迷宫,如果采用单手法则,你就会沿着最外层的那堵墙转圈,进不到迷宫内部去,就是俗称的“鬼打墙”。这样走了一圈又回到原地的路叫回路。
②介绍多联通迷宫。
师:像这样的在入口处或目的地有回路的迷宫,叫多联通迷宫。
2.探究多联通迷宫的走法。
师:如果你来到一个多联通迷宫里,又看不到终点,怎么才能走出来呢?(生各抒己见)
师根据学生的回答,引导:先沿着墙壁走,遇到岔路做个记号,按照一定的顺序,先选择最边上的路,如果是死路或者回到原地的话,就回到岔路口,排除刚才走过的那条,选择与之相邻的路。
3.介绍特来莫科斯法。
师:以上这种方法叫特来莫科斯法。它是在几百年前,由一个叫特来莫科斯的人在玩迷宫的时候发明的。谁能用自己的语言介绍一下特来莫科斯法?
4.编歌谣记忆特来莫科斯法。
师:老师把特来莫科斯法编成了一句歌谣:沿着墙壁一直走,遇到岔路做记号,死路、回路就排除,回到岔路选新路,选路记得按顺序。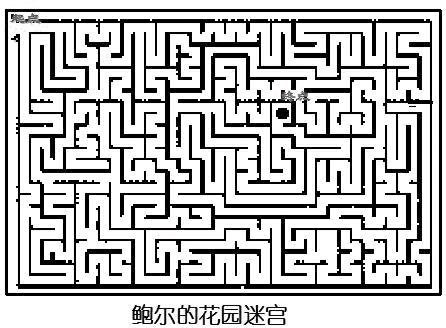
5.介绍法国数学家卢卡斯和他的名著《趣味数学》。
师:用特来莫科斯法可以走出所有的迷宫,所以,1882年,法国数学家卢卡斯在他的名著《趣味数学》中还特意介绍了这种方法。
6.介绍鲍尔的花园迷宫。
师:用这个方法,我们可以走一个迷宫试试。这是100多年前英国数学家鲍尔在自己的花园里建造的迷宫(如图所示)。这个迷宫的入口在左上角,目的地是迷宫中的黑点。
7.学生讨论鲍尔的花园迷宫的走法。师:这个迷宫复杂吗?
生:是的,看得人眼花缭乱。
师:确实非常复杂!而且你站在花园迷宫中,不知道终点在哪里。你觉得走这样复杂的迷宫时要注意什么?
生:沿着墙壁一直走,遇到岔路做记号,死路、回路就排除,回到岔路选新路,选路记得按顺序。
学生活动:走鲍尔的花园迷宫。学生活动完毕进行作业展示,交流走法。
8.课件展示鲍尔的花园迷宫的走法。
师小结:是的,走迷宫的方法有很多,特来莫科斯法有可能使你走出迷宫的路径相当繁琐,但这个办法是十分保险而没有风险的。同学们可以根据不同的情况选择合适的方法。
9.介绍数学家欧拉和拓扑学。
师:同学们,走迷宫好玩吗?在玩中可藏着大学问呢!数学家欧拉就是通过研究迷宫的数学问题创建了数学中的重要分支———拓扑学。其实,我们刚才就是运用拓扑学的知识解决走迷宫问题的。
10.学生自己玩迷宫游戏。
五、结语。
师:今天,我们走进了有趣的迷宫世界,发现其中藏着很多的奥秘。老师还收集了一些世界著名的迷宫图(课件演示),有兴趣的同学可以尝试走一走。今天的课就到这里。
(作者单位:长沙市长郡雨花外国语学校)
