尘埃等离子体的谐振问题研究

徐彬 李辉,2 许正文 马征征 王占阁 吴健

(1. 中国电波传播研究所 电波环境特性及模化技术重点实验室,青岛 266107;2. 哈尔滨工业大学物理系,哈尔滨 150001)

尘埃等离子体的谐振问题研究

徐彬1李辉1,2许正文1马征征1王占阁1吴健1

(1. 中国电波传播研究所 电波环境特性及模化技术重点实验室,青岛 266107;2. 哈尔滨工业大学物理系,哈尔滨 150001)

基于尘埃等离子体的色散关系,在不考虑高/低频近似的情况下,推导了尘埃等离子体谐振频率和增长率的表达式,讨论了尘埃质量、尘埃密度和载波频率对谐振过程的影响,给出了尘埃等离子体谐振过程的基本物理规律. 典型火箭喷焰等离子体参数条件下,考察了高速尘埃粒子组分的引入对谐振过程的影响. 仿真结果表明,尘埃速度在1 km/s的条件下即可激发谐振过程,谐振频率约为3 kHz. 尘埃等离子体谐振机理模型和高速组分影响机制的得出对深入理解尘埃等离子体的物理过程和火箭喷焰的异常衰减机制具有重要意义.

尘埃等离子体;介电函数;色散关系;谐振

DOI 10.13443/j.cjors.2016112601

引 言

尘埃等离子体物理问题是近年来伴随空间科学、航天航空技术等领域的发展逐渐暴露出来的一个较为突出的基础理论问题. 其中一个重要难点即是火箭喷焰形成的高密度尘埃等离子体异常衰减现象的物理机制[1-3]. 火箭喷焰是由电子、离子、分子以及尘埃粒子组成的弱电离尘埃等离子体,对固体火箭喷焰来说,其主要尘埃成分是Al2O3颗粒, 温度在几百K到三千K之间, 其中分子的浓度远大于电子和离子的浓度,电子与离子的浓度基本相等并远大于Al2O3尘埃粒子的浓度. 这一复杂的等离子体系统通过三种机制对穿越其中的电波产生影响:一是常规等离子中电子与中性气体成分碰撞造成的衰减,这可以使用传统的AH公式进行解释[4-5];二是带电尘埃粒子造成的附加碰撞形成的电磁波衰减,这主要从尘埃等离子体的介电特性角度进行解释[6-10],需要考虑电子和带电尘埃粒子间的弹性库伦碰撞和非弹性碰撞,考察带电尘埃的引入对等离子体电导率的影响,进而形成增加电磁波的吸收率衰减机制； 三是高速尘埃触发的不稳性形成的相干结构造成的衰减. 这就要求我们理解等离子体谐振过程的触发机制[11-12]. 对常规的电子-离子等离子体系统来说,大量的文献[13-21]从流体力学方程和动力理论等角度探讨了谐振和波动过程的发生发展机制. 然而尘埃等离子体的谐振问题,特别是从动力理论出发考察尘埃等离子体的谐振问题的工作则较少被涉及[22],相关的理论体系也尚未被建立.

本文给出了尘埃等离子体的色散关系,在不考虑高/低频近似的情况下,推导了尘埃等离子体谐振频率和增长率的表达式,考察了高速尘埃粒子组分的引入对谐振过程的影响. 并在此基础上,讨论了尘埃参数对谐振过程的影响.

1 尘埃等离子体的色散关系

一般地,等离子体由电子和离子两种带电粒子成分组成,其介电函数包含电子极化率和离子极化率的影响[23]:

ε(k,ω)=1+χe(k,ω)+χi(k,ω).

(1)

式中:χe(k,ω)和χi(k,ω)分别为电子和离子极化率;k为波矢量;ω为角频率. 对尘埃等离子体来说,新的带电成分的引入,对等离子体的介电特性可以产生严重的影响．引入尘埃项的影响,介电函数可以写为[24]

ε(k,ω)=1+χe(k,ω)+χi(k,ω)+χd(k,ω).

(2)

式中:χd(k,ω)为尘埃极化率．因此,尘埃等离子体的色散关系为

ε(k,ω)=1+χe+χi+χd=0.

(3)

式中:ω=ωr+iγ，ωr为谐振频率，γ为增长率(阻尼率). 分别求解介电函数实部和虚部等于0,即可获得谐振频率和增长率. 由于通常有增长率远小于谐振频率,γ≪ωr,因此我们可以将介电函数作小量展开,保留一阶小量,有[23]

iεi(k,ωr)=0.

(4)

因此色散关系可以写为

(5)

这种简化方式使得求解规避了复奇点积分的问题,极大地提高了计算的效率和稳定性. 对具有速度分布的粒子系统来说,电子、离子和尘埃的极化率分别为[24]:

(6)

(7)

(8)

式中:pe=v/vthe;pi=v/vthi;pd=v/vthd;ξe=ω/(kvthe);ξi=ω/(kvthi);ξd=ω/(kvthd)；vthe，vthi和vthd分别为电子、离子和尘埃的热速度;λDe,λDi和λDd分别为电子、离子和尘埃的德拜长度;ge,gi和gd为电子、离子和尘埃的归一化分布函数. 若粒子系统处在平衡态,其分布为麦克斯韦分布,此时,极化率可以写成:

(9)

(10)

(11)

对具有高速尘埃成分的等离子体系统,需要引入漂移速度的影响,此时尘埃极化率可以写为:

(12)

式中，

ξ′d=ξd-vd/vthd，

(13)

vd为高速尘埃成分漂移速度.将式(9)、(10)、(12)、(13)代入式(5),即可求解尘埃等离子体系统的谐振频率和增长率.

2 谐振过程数值仿真与分析

为考察尘埃等离子体谐振过程的特征规律,利用式(9)～(11)计算了电子、离子和尘埃的极化率,计算结果如图1所示.其中横轴为载波频率,纵轴为极化率的绝对值.计算使用的主要参数为:尘埃密度 1×1013m-3,尘埃温度2 000 K,尘埃半径10 nm,电子密度1×1018m-3,电子温2 000 K. 为同时考察尘埃谐振区、离子谐振区和电子谐振区的极化率特征,横轴和纵轴我们都使用了对数坐标系. 从图1可以看到,无漂移条件下,电子、离子和尘埃的极化率均随载波频率的增加而减小,尘埃极化率的零点为0.1 Hz量级,离子极化率的零点为10 kHz量级,电子极化率的零点为1 MHz量级,在零点位置极化率的绝对值发生翻转,此后迅速增大.

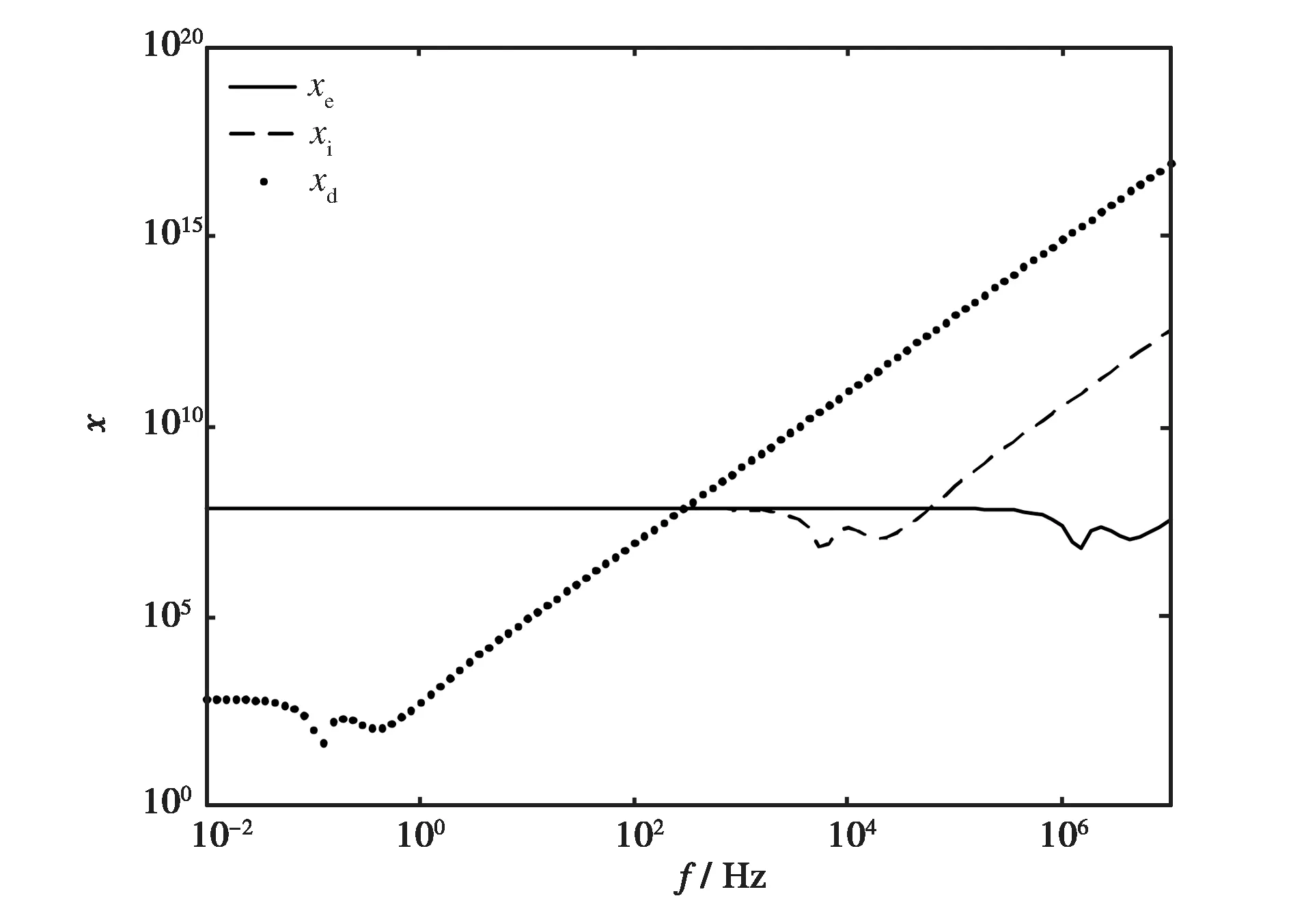
图1 极化率随载波频率的变化

依据式(2)给出的色散关系可以得知,电子、离子和尘埃极化率出现负值时,才能使介电函数为零,发生谐振.在低频段(～0.1 Hz)的尘埃谐振区,尘埃极化率率先出现负值,但电子和离子的极化率在107量级,尘埃极化率(～102)是相对小量,因此在该频段不会出现谐振. 在电子谐振区,由于尘埃和离子的质量远大于电子质量,因此考察电子谐振区的谐振行为,可以忽略尘埃和离子的影响. 电子极化率零点位置附近(1+χe=0),即为电子谐振区的谐振频率,通常称为朗缪尔频率. 也就是说,常规尘埃等离子体条件下,尘埃成分的引入,主要对离子谐振区的谐振行为产生影响. 无尘埃情况下,60 kHz附近,离子极化率和电子极化率出现交叉,在该频段发生谐振. 引入尘埃情况下,在300 Hz频段,尘埃极化率减小到-107量级,尘埃极化率与另外两种极化率出现交叉,这意味着介电函数在这一区间内第一次出现零点,具备谐振频率.

从仿真结果可以得出,尘埃组分的引入极大地减小了谐振频率,且该谐振频率的值主要由尘埃极化率决定,主要受尘埃质量、尘埃密度和载波频率影响.依据式(5),我们分别求解了不同参数条件下的谐振频率和增长率,图2～5给出了上述参数对谐振频率和增长率的影响.从图中可以看到,随载波频率的增大谐振频率增大,阻尼率减小.随尘埃半径的减小,尘埃颗粒的质量变小,谐振频率从～100 Hz量级增加到10 kHz量级. 也就是说随尘埃变小,尘埃颗粒趋离子化,等离子体的谐振频率也更接近电子-离子等离子体系统的谐振频率. 增长率随尘埃尺寸的变化规律并不一致,出现先增大后减小的特征. 随尘埃密度的增加,尘埃粒子的影响更为显著,谐振特性与电子-离子等离子体系统的区分更为显著(图4). 这是因为等离子体系统中尘埃比例越高,其主导作用越显著,离子所起到的作用相对变小,具体表现为谐振频率减小. 随尘埃密度的变化,增长率的变化是单调的,增长率的绝对值增大,但增长率减小. 需要说明的是,上面的仿真结果表明,无论如何增长率均为负值,也就是说谐振过程是阻尼的,只有尘埃的半径很大、密度很高、载波频率很低的条件下,增长率才趋于零值.

常规的尘埃等离子体条件下,尽管存在本征的谐振过程,但这些谐振过程不会持续下去,谐振幅度更不会随时间增长,阻尼作用会使得这些谐振迅速衰减. 从式(5)可以得知,阻尼率由介电函数的虚部和谐振频率处介电函数实部的梯度共同决定. 一般地,介电函数的虚部为负值,要保证增长率大于零,需满足介电函数实部的梯度大于零. 更为清晰的物理图像是:对谐振频率为ω的粒子波,其相速度为ω/k. 由于相速度两侧的粒子数目不同,对处在平衡态的等离子体系统来说,速度为(ω-Δω)/k的粒子数目大于速度为(ω+Δω)/k的粒子数目,而速度大于ω/k的粒子向波传递能量,速度小于ω/k的波向粒子传递能量,更多的能量流向是波向粒子的,因此谐振或波动过程是阻尼的. 也就是说,为保证增长,要求(ω-Δω)/k的粒子数目小于速度为(ω+Δω)/k的粒子数目,此时粒子存在Bump-on-tail分布,或者说存在高速尘埃成分,式(12)～(13)给出了对应的极化率的表达式.利用式(12)～(13)给出了谐振频率和阻尼率随尘埃漂移速度的变化(图6～7). 从图中可以看到,随着漂移速度的增加,介电函数的虚部的绝对值迅速减小,而鉴于处在分布函数中心附近,因此介电函数实部的梯度绝对值变化较小,整体表现为增长率减小. 当速度增加到ωr/k时,介电函数实部的梯度开始大于零,此时增长率变为正值,谐振与波动过程正式被激发. 而随着速度进一步增大,分布函数的尾部处在谐振频率处,分布函数的梯度变小,谐振频率两侧的粒子数目趋同,增长率又逐渐降低. 对谐振频率来说,随漂移速度的增大,谐振频率增大,在突跳点,谐振频率等于零,此后继续单调增加.

图2 尘埃半径对谐振频率的影响

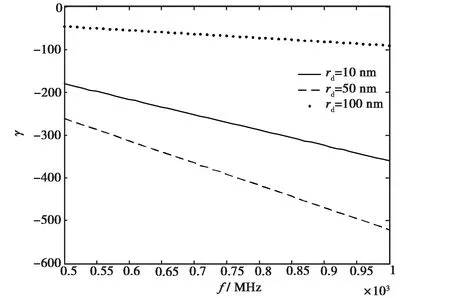
图3 尘埃半径对增长率的影响

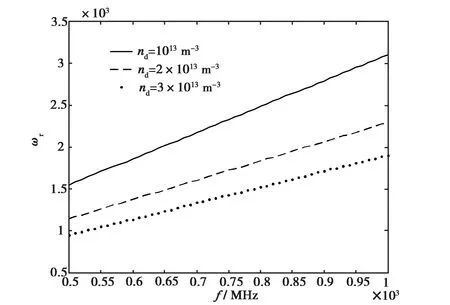
图4 尘埃密度对谐振频率的影响

图5 尘埃密度对增长率的影响

图6 谐振频率随尘埃漂移速度的变化

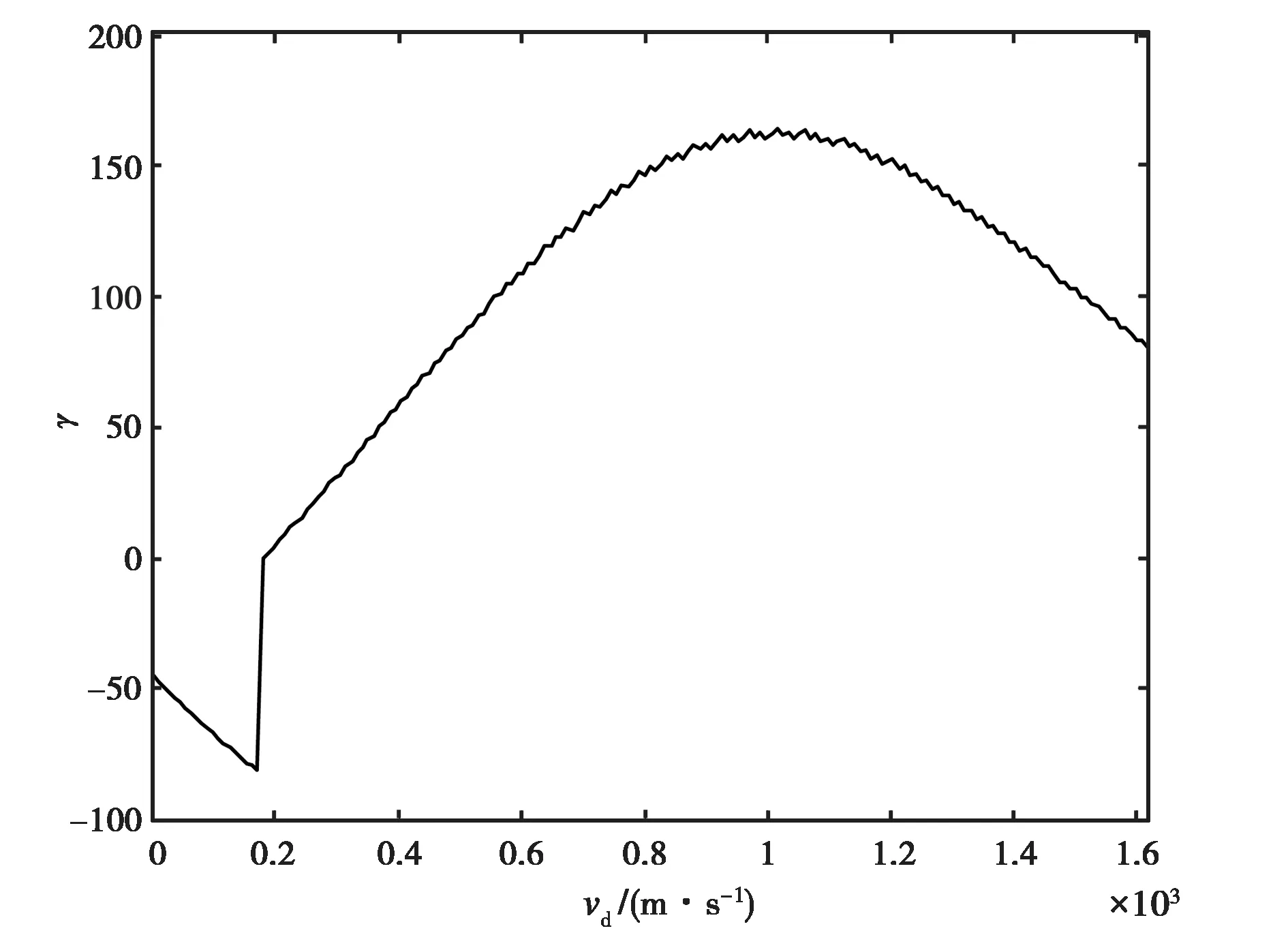
图7 阻尼率随尘埃漂移速度的变化

3 结 论

尘埃等离子体的谐振与波动过程问题是一个基本的物理问题,构建其机理模型,对深入理解尘埃等离子体的物理规律具有十分重要的意义. 在火箭喷焰等高速尘埃等离子体条件下,一方面尘埃的掺杂使原电子-离子等离子体系统的介电特征发生了根本性的变化,另一方面高速尘埃组分的存在,使得不稳定性和波动过程极易被激发,而这些因素共同造就了火箭喷焰对通信和雷达信号的强衰减. 本文给出了尘埃等离子体的色散关系,在不考虑高/低频近似的情况下,推导了尘埃等离子体谐振频率和增长率的表达式,讨论了尘埃质量、尘埃密度和载波频率对谐振过程的影响,给出了尘埃等离子体谐振过程的基本物理规律. 典型火箭喷焰等离子体参数条件下,文中给出了高速尘埃粒子组分的引入对谐振过程的影响. 仿真结果表明,尘埃速度在1km/s的条件下即可激发谐振过程,谐振频率约为3kHz. 本文给出了尘埃等离子体谐振过程的理论研究结果,在此基础上,开展与相关试验数据的对比研究,进而对火箭喷焰的异常衰减机制给出合理的解释是我们进一步所要完成的工作.

[1]SMOOTLD,SELIGAJJ.Rocketexhaustplumeradarattenuationandamplitudephasenoise[J].Journalofspacecraftandrockets, 1967, 4(6): 774-780.

[2]SMOOTLD,WILLIAMSJW.Refinedmeasurementsofexhaustplumeinducedradaramplitudeandphasenoise[J].Journalofspacecraftandrockets, 1968, 6(11): 1268-1273.

[3]SELIGATJ.Rocketexhaustplumeradarattenuationandamplitude/phasenoise[J].Journalofspacecraftandrockets, 1967, 4(6): 774-780.

[4]GUREVICHAV.Nonlinearphenomenaintheionosphere[M].Berlin:Springer, 1978.

[5]SHEFFIELDJ.Plasmascatteringofelectromagneticradiation[M].NewYork:AcademicPress, 1975.

[6]LIH,WUJ,ZHOUZX,YUANCX.Propagationofelectromagneticwaveindustyplasmaandtheinfluenceofdustsize[J].Physicsofplasmas, 2016, 23:073702.

[7]LIH,WUJ,ZHOUZX,YUANCX,etal.Thedielectricfunctionofweaklyionizeddustyplasmas[J].Physicsofplasmas, 2016, 23:073301.

[8]LIH,WUJ,YUANCX,etal.Theelectricalconductivityofweaklyionizedplasmacontainingdustparticles[J].PhysicslettersA, 2016, 380:2540-2543.

[9]LIH,WUJ,ZHOUZX.Theformationofmultiplelayersoficeparticlesinthepolarsummermesopauseregion[J].Annalesgeophysicae, 2016, 34:117-122.

[10]石雁祥,王菊,吴健等. 对两种弱电离尘埃等离子体特征参量的定量估计. 电波科学学报. 2008,23(1): 95-99.

SHIYX,WANGJ,WUJ,etal.Characteristicparametersestimationoftwoweaklyionizeddustyplasma[J].Chinesejournalofradioscience, 2008, 23(1): 95-99. (inChinese)

[11]SUMMERSD,THORNERM.Themodifiedplasmadispersionfunction[J].Physicsoffluids, 1991 (B3): 1835-1847.

[12]SUMMERSD,THORNERM,MATSUMOTOH.Evaluationofthemodifiedplasmadispersionfunctionforhalf-intergralindices[J].Physicsofplasmas, 1996, 3: 2496-2501.

[13]GARCIAG,FORMEF.Akineticmodelforrunawayelectronsintheionosphere[J].Annalesgeophysicae, 2006, 24:2391-2401.

[14]GUREVICHAV,GUREVICHHC,CARLSONY,etal.Langmuirturbulenceinionosphericplasma[J].PlasmaphysicsReports, 2004, 30(12):995-1005.

[15]STUBBEP.Modifyingeffectsofastrongelectromagneticwaveuponaweaklyionizedplasma:akineticdescription[J].Radioscience, 1981, 16 (3):417-425.

[16]RIETVELDMT,ISHAMB,GRYDELANDT,etal.HF-pump-inducedparametricinstabilitiesintheauroralE-region[J].Advanceinspaceressearch, 2002, 29, 9:1363-1368.

[17]MJØLHUSE.Parametricinstabilitiesoftrappedupper-hybridoscillations[J].Journalofplasmaphysics, 1997, 58, 4:747-769.

[18]赵正予,魏寒颖. 参量激励过程中三波耦合的一般色散关系(Ⅰ):最容易激励参量不稳定性的频率和波矢条件[J]. 空间科学学报,2004, 24(6): 441-447.

ZHAOZY,WEIHY.Generaldispersionrelationforthethree-waveprocessofparametricexcition(I):ThepreferredexcitationofanelectronLangmuirwaveandanionacousticwave[J].Chinesejournalofspacescience, 2004, 24(6): 441-447. (inChinese)

[19]赵正予,魏寒颖. 参量激励过程中三波耦合的一般色散关系(Ⅱ):一般色散关系以及泵波阈值和增长率[J]. 空间科学学报,2004,25(1):17-22.

ZHAOZY,WEIHY.Generaldispersionrelationforthethree-waveprocessofparametricexcitation(Ⅱ):Thebasicformula,thefieldthresholdandthegrowingrate[J].Chinesejournalofspacescience, 2004,25(1): 17-22. (inChinese)

[20]邓峰,赵正予,周晨，等. 高频加热中低纬电离层激励不稳定性研究[J]. 地球物理学报,2010,53(1):10-21.

DENGF,ZHAOZY,ZHOUC,etal.ResearehofionosphericinstabilityexeitedinmidandlowlatitudesHFheating[J].Chinesejournalofgeophysics, 2010, 53(1): 10-21. (inChinese)

[21]徐彬,吴健,LAHOZC,等. 热流效应对场向电流确定的影响[J]. 空间科学学报,29(6):573-579.

XUB,WUJ,LAHOZC,etal.Effectoftheheatingflowonthedeterminationofthefield-alignedcurrents[J].Chinesejournalofspacescience, 2009, 29(6):573-579. (inChinese)

[22]马征征,徐彬,许正文. 尘埃等离子体混合模型中电荷-电势问题的迭代法求解[J]. 电波科学学报,2015,30(3):549-553.

MAZZ,XUB,XUZW.Slovingcharge-potentialissueindustyplasmahybridmodelbyiterationmethod[J].Chinesejournalofradioscience, 2015,30(3):549-553. (inChinese)

[23]SHEFFIELDJ.Plasmascatteringofelectromagneticradiation[M].NewYork:AcademicPress, 1975.

[24]徐彬,李辉,王占阁,等. 高密度尘埃等离子体的非相干散射理论研究[J]. 物理学报,2017,66(4):049401.

XUB,LIH,WANGZG,etal.Studyonincoherentscattertheoryofhighdensitydustyplasma[J].Actaphysicasinica, 2017,66(4):049401. (inChinese)

李辉 (1981-),男,江西人,现为哈尔滨工业大学博士研究生,主要从事尘埃等离子体理论和仿真研究．

许正文 (1971-),男,安徽人,中国电波传播研究所研究员,博士,主要从事电离层波传播方向研究．

Study on resonance process of dust plasma

XU Bin1LI Hui1,2XU Zhengwen1MA Zhengzheng1WANG Zhange1WU Jian1

(1.NationalKeyLaboratoryofElectromagneticEnvironment,ChinaResearchInstituteofRadiowavePropagation,Qingdao266107,China; 2.DepartmentofPhysics,HarbinInstituteofTechnology,Harbin150001,China)

Based on the kinetic theory, the dispersion relation of dust plasma is presented. Without the high/low frequency approximation, the formulas of resonance frequency and growth rate are given, and the effects of dust mass, density and carrier frequency on resonance process are discussed. The basic physical laws of dust plasma resonance process are obtained. The influence of high velocity dust particles on resonance process for the typical rocket plume is analyzed. The simulation results show that the resonance process can be excited with a dust velocity of 1 km/s, and the resonance frequency is 3 kHz. The mechanisms of dust plasma resonance and the effect of high velocity dust are of great significance for understanding the physical process of dust plasma and abnormal decay of rocket plume.

dust plasma; dielectric function; dispersion relation; resonance process

2016-11-26

国家自然科学基金(41004065，61601419，11672068)；电波环境特性及模化技术重点实验室基金(2014000001)

10.13443/j.cjors.2016112601

P352

A

1005-0388(2017)01-0016-06

徐彬 (1982-),男,辽宁人,中国电波传播研究所高级工程师,博士,主要从事尘埃等离子体理论和空间等离子体探测研究．

联系人： 徐彬 E-mail: jasur82@163.com

徐彬, 李辉, 许正文,等. 尘埃等离子体的谐振问题研究[J]. 电波科学学报,2017,32(1):16-21.

XU B, LI H, XUE Z W,et al. Study on resonance process of dust plasma[J]. Chinese journal of radio science,2017,32(1):16-21.(in Chinese). DOI: 10.13443/j.cjors.2016112601