基于有限元方法的流致振动数值模拟

杨 凡

(西南交通大学, 四川成都 610031)



基于有限元方法的流致振动数值模拟

杨 凡

(西南交通大学, 四川成都 610031)

文章基于ANSYS Workbench与CFX有限元分析软件，采用双向流固耦合方法，以横向流作用下的单根直管为基本分析对象，来研究单管的流致振动响应情况。通过建立三维流固耦合模型，利用LES大涡模拟，对较大雷诺数时均匀来流垂直流过单管的情况进行分析，并选取不同流速下，得到了单管结构随速度的变化以及流场特性。结果表明，换热器管道等必须将流速控制在一定范围内，否则会造成结构损坏。借助数值模拟软件，可以大大提高数值仿真的效率。

流致振动； 双向流固耦合； 数值模拟； Workbench；

流固耦合基于流体力学与固体力学基础之上，涉及到多个物理场之间的相互作用，流体接触到结构对结构产生压力从而结构产生形变，变形的结构反之也会改变流场的分布，进而不断重复这个过程。

在生产与生活中管束振动问题不可忽视，实际应用中主要产生流致振动的部件可以简化为圆柱结构，流体对圆柱结构的冲刷会引起部件的损伤，从而对结构总体安全带来严重的危害[1]。流体引发的振动从运动方向上可以分为纵向流和横向流，纵向流沿轴线方向，横向流垂直于轴线方向，即使在流速不大时，横向流也会引发管的振动。不同流速下引发振动的机理主要有涡激振动、湍流抖振、流体弹性不稳定性和声共振4种[1]。

前人对流致振动各项机理的研究做了大量的工作，主要通过实验数据确定流体力系数，但由于所需参数过多，因此有很强的局限性[2]。随着数值方法和计算机技术的不断发展， 已经可以利用有限元软件对其进行模拟分析。王亚玲等[3]发现高Re时圆柱周围的流动具有明显的三维特性；德国的M·Breuer采用大涡模拟方法对高雷诺数下孤立圆柱绕流问题进行了三维的数值模拟,结果表明采用大涡模拟方法进行圆柱绕流的三维数值计算和实验结果吻合的较好[4]。一个完整的流固耦合分析包含了单独的结构分析、单独的流体场分析和耦合边界分析三个过程。

1 数值计算方法研究

经典的流固耦合系统分为强耦合和弱耦合两大类，整体趋向于利用N-S方程与非线性结构动力学求解。一般使用迭代求解，也就是在流场、结构上分别求解，在各个时间步之间耦合迭代，收敛后再向前推进。同时考虑大变形带来的网格变化问题，由于结构的变形，使得流场的计算域发生变化，要考虑流场网格随时间变形以适应耦合界面的变形。

流固耦合问题一般分为两类：一类是流-固单向耦合，一类是流-固双向耦合。单向耦合应用于流体对固体作用后，固体变形不大，即流体的边界形貌改变很小，不影响流体分布的；与单向流固耦合不同，流体的结果在输出给结构以后，固体结构的计算结果也反向对流体产生作用，当固体结构变形比较大，导致流体的边界形貌发生改变后，流体分布会有明显变化时，单向耦合显然是不合适的。因此本文选用双向流固耦合分析方法，必须先设置好FSI(流固耦合表面)，才能在在ANSYS Workbench中的Transient Structural(ANSYS)与Fluid Flow(CFX)对结构与流体设置并对响应进行分析[5]。

1.1 流场分析

本文使用三维粘性、不可压缩的流体，利用大涡模拟方法求解流体区域。流体服从流体力学基本方程，不考虑热量交换，遵守质量、动量守恒方程，可表示为：

(1)连续性方程：

(1)

(2)运动方程：

(2)

式中：ui为在方向上流体的速度分量；t为时间；ρ为流体密度；p为压力；v为流体运动系数。

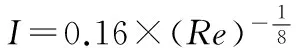
1.2 结构分析

对结构进行有限元离散，某时刻结构的动力学方程为：

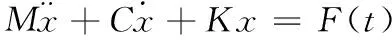
(3)

式中：M为质量矩阵；C为阻尼矩阵；K为刚度矩阵；x为位移矢量；F(t)为流体运动引起的荷载。

1.3 耦合分析

对于多场耦合分析，将流体场和结构场作为两种物理环境耦合，并将前一步的耦合结果作为边界条件作用在新的耦合场上，自动交替实现。本文使用流体推动固体的分析，固体结构变形反之影响流体，使用双向流固耦合方法，打开大变形选项，流体与固体使用相同的耦合时间步，设定动网格，设置结构与流体接触面为流固耦合面(图1)。

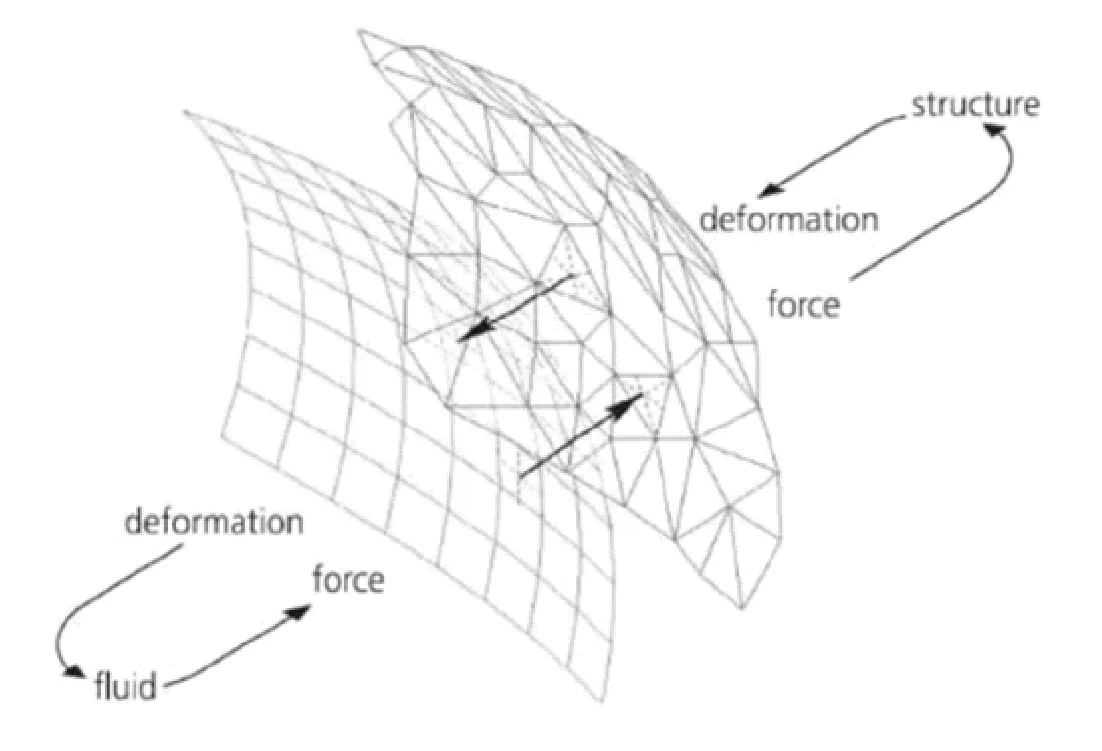
图1 流固耦合结构域和流体域交界面

2 物理模型建立及参数设置

2.1 物理模型

本文使用直管束流固耦合振动的数值模拟[6]中的模型参数，管长L=0.5 m，外径D=0.01 m，内径D=0.095 m，弹性模量E=10 GPa，泊松比v=0.3，管子的密度ρ0=6 500 kg/m3，阻尼比ζ=0.047。流体为水，密度ρ=998.2 kg/m3，动态粘度μ=0.001003 Pa·s。流速v从0.5 m/s开始变化。

本文所需流场大小对数值模拟结果有很大影响，为了简化计算并且使结果尽可能准确，参照文献三维圆柱体涡激振动[7]、三维圆柱体DNS模拟方法[8]等，当轴线选择距离出口15D以上时，压强接近于零，宽度大于8D时，碰壁现象消失，高度大于πD时足以正确描述漩涡特性。最终选择20D×30D×10D。

模型建立如图2所示，其中，入口采用速度入口边界条件，出口为压力出口，管外壁为FSI，同时设置为动网格边界，划分结构化网格，时间步长选为0.00025 s，总共计算0.5 s。流体域与固体域必须选用相同的时间步依次迭代。

2.2 流固耦合设置

ANSYS收购并组合了CFX，使得新开发的ANSYS Workbench在不需要第三方软件的情况下实现双向流固耦合，结果可靠。对流体诱导振动问题的数值模拟需要考虑流场模拟、结构振动模拟、流体-结构交互作用模拟和数据处理四步。本文使用大涡模拟，它将比网格尺寸大的大涡运动通过N-S方程计算，将比网格尺寸小的运动建立亚格子模型并通过此建立与大涡运动的关系，其求解范围更大，结果更具普遍适应性[9-10]，现有的计算机条件下对较高的雷诺数和复杂湍流模型的模拟较好。

图2 模型及网格

首先在Design Modeling建立如图2的三维模型。将模型导入workbench中的Mechanical部分，先Suppress流场部分，对结构进行定义并基于ICEM CFD划分六面体网格，设置约束及流固耦合面。再对流体部分定义进出口及对称面，划分网格，利用setup进行双向流固耦合设置，定义计算域，赋初始值，定义求解器属性，并设置输出控制及监测点。最后在CFX-Solver里设置并行环境下运算，在CFX-Post中查看结果并分析。

4 计算结果分析

基于数值模拟结果对单管流致振动特性进行分析，引入位移之比x/y，其随时间变化如图3所示。图4～图10为不同流速下的压力和速度云图。由图像可以看出，在流速较小(v≤2 m/s)时，管子先处于平衡状态；当流速继续增大，流体与管发生共振，管的位移也开始不断增大；当流速增大至超过3 m/s以后，管子开始发生失稳；当速度v≥3.5 m/s以后，管开始发生剧烈不规则变化。

图3 不同流速下管的位移之比

图4 v=0.5m/s

图5 v=1m/s

图6 v=2m/s

图7 v=2.5m/s

图8 v=3m/s

本文实现了单根管在横向流作用下的耦合仿真分析，得到了结构在不同流速下的响应。结果表明，换热器管道等必须将流速控制在一定范围内，否则会造成结构损坏。借助数值模拟软件，可以大大提高数值仿真的效率。

图9 v=3.5m/s

图10 v=4.5m/s

[1] Weaver D S，Ziada S，Au-Yang M K，Chen S S，Paidoussis M P，Pettigrew M J．Flow-induced vibrations in power and process plant components—progress and prospects[J]． Journal of Pressure Vessel Technology, 2000, 122(3):339-348．

[2] Eisinger F L，Rao M S M ，Steininger D A，Haslinger K H．Numerical simulation of cross-flow-induced fluidelastic vibration of tube arrays and comparison with experimental results[J]. Journal of Pressure Vessel Technology, 1995, 117(1):31-39．

[3] 王亚玲, 刘应中, 缪国平. 圆柱绕流的三维数值模拟[J]. 上海交通大学学报, 2001, 35(19):1464-1469.

[4] BREUERM. A challenging test case for large eddy simulation high Reynolds number circular cylinder flow[J]. Heat and Fluid Flow, 2000, (21):648-654.

[5] 宋学官, 蔡林, 张华. ANSYS流固耦合分析及工程实例[M]. 北京：中国水利水电出版社, 2012.

[6] 冯志鹏，张毅雄，臧峰刚. 直管束流固耦合振动的数值模拟[J]. 应用数学和力学, 2003, 34(11):1165-1172

[7] Pontaza J P, Chen H C. Three-dimensional numerical simulations of circular cylinders undergoing two degree-of-freedom vortex-induced vibrations[C]. Proceedings of 25th international Conference on Offshore Mechanics and Arctic Engineering. Germany: Hamburg, 2006.

[8] Dong S, Karniadakis G E. DNS of flow past a stationary and oscillating cylinder at Re=10000[J]. Journal of Fluids and Structures, 2005. (20):519- 531.

[9] Benhamadouche S，Laurence D． LES，coarse LES，and transient RANS comparisons on the flow across a tube bundle[J]. International Journal of Heat and Fluid Flow, 2003, 24(4) : 470-479．

[10] Anagnostopoulos P．Numerical study of the flow past a cylinder excited transversely to the incident stream—part 1: lock-in zone，hydrodynamic forces and wake geometry[J]. Journal of Fluids and Structures，2000, 14(6) : 819-851．

杨凡(1992～)，女，工学硕士，研究方向为流固耦合动力学。

TU311.3

A

[定稿日期]2017-03-07