拱形排列微型桩抗滑机理研究
2017-05-18姚禹龙肖维民张志伟潘汝江游晶越
姚禹龙, 肖维民, 张志伟, 潘汝江, 游晶越
(1. 四川农业大学土木工程学院,四川都江堰 611830;2. 四川建筑职业技术学院铁道工程系, 四川成都 610399)
拱形排列微型桩抗滑机理研究
姚禹龙1, 肖维民1, 张志伟2, 潘汝江1, 游晶越1
(1. 四川农业大学土木工程学院,四川都江堰 611830;2. 四川建筑职业技术学院铁道工程系, 四川成都 610399)
传统的微型桩布置形式在应对较复杂地形时易发生桩身受力不均、整体性降低等情况。利用拱结构应力分布均匀、主要承受轴向压力等特点,将微型桩按拱形排列布置,桩顶用连系梁约束以共同承担滑坡推力,即形成拱形排列微型桩抗滑结构。该结构用抗压性能好的拱形混凝土刚性连系梁承受轴向压力,充分发挥受压构件的作用,使桩身受力均匀。文章选取不同矢跨比情况下排列的微型桩体系,建立协调方程对连系梁与微型桩的受力进行分析。通过算例得出结论:拱形连系梁矢跨比增加,对微型桩的约束越明显。
微型桩; 内力分析; 拱形排列
1 国内对微型桩的研究状况
微型桩的桩径一般小于400 mm且具有较大长细比,通常采用钻孔、注浆等工艺进行施工。由于微型桩的孔径较小,因此在工程中具有设计灵活性大、施工方便快捷等优势。近年来,微型桩作为一种新型结构越来越多的运用于中小型滑坡防治、边坡加固等实际工程中[1]。国内学者对微型桩的抗滑计算理论研究取得了一些成果,龚健等人[2]对微型桩单桩与群桩布置进行了水平荷载试验;冯君[3]针对微型桩加固顺层岩质边坡的作用机理以及计算理论进行了研究,提出了微型桩单桩抗剪强度公式;肖世国[4]根据微型桩组合抗滑结构的特点,研究了其抗滑受力情况;孙书伟[5]研究了微型桩群-土相互作用机制并推导出计算公式;周德培[6]按照桩-土相互作用原则讨论了顶梁固定微型桩的组合结构的抗滑机制并按照横向约束的弹性地基梁法提出了设计计算理论;肖维民[7]对微型桩单桩与群桩的不同抗滑情况做了相关研究。与此同时,许多学者也进行了微型桩抗滑的相关模拟实验,胡毅夫[8]通过模型试验总结了微型桩双排单桩与组合桩在加固边坡时的抗滑特性;闫金凯[9]以黄土为滑坡介质,完成一系列微型桩与滑坡体相互作用的模型试验;孙书伟[10]用模拟实验的方法研究了框架微型桩结构抗滑特性;白晨光[11]对具有抗弯功能的微型桩在基坑支护中的设计与施工进行了研究;朱本珍[12]对微型桩群加固堆积层滑坡的加固效果和受力特性进行原位试验。
目前对微型桩的抗滑计算理论的研究成果较多,但对其在不同布置形式下微型桩的受力模式与抗滑理论研究较少,本文针对目前微型桩不同布置形式的研究成果,总结出工程中常用的几种微型桩布置的结构形式,并讨论其布置形式的优缺点。对于滑坡推力较大且地质条件复杂的坡面,微型桩传统布置形式很难满足设计要求。与此同时,一些学者对拱形排列抗滑桩在大型工程中的应用做了一定研究[13],但是在微型桩上的应用较少且理论研究十分匮乏。
本文提出一种新型微型桩布置形式——拱形排列微型桩布置体系,该体系能发挥混凝土拱形连系梁受压性能好的特点,使结构受力均匀,约束桩身位移,可运用在特殊的中小型边坡加固工程中。
2 拱形排列微型桩抗滑机理研究
2.1 结构特性分析
将微型桩按拱形放置,使之成为一种在地面水平放置的拱结构。拱身承受边坡滑较大的推力,拱脚处则选用较大截面的桩型以承受水平推力,如图1所示。相对于传统布置形式的微型桩,空间拱型排列微型桩体系有以下优点:

图1 拱形排列抗滑微型桩结构
(1)利用拱结构应力分布较为均匀、主要承受轴向压力的特点,用抗压性能好的混凝土刚性连系梁承受轴向压力,充分发挥受压构件的作用,达到合理运用材料的目的。
(2)连系梁增加了体系的稳定性,拱结构比桁架结构具有更大的力学优点,有效控制桩顶位移。
(3)利用拱结构卸荷特点,使荷载通过梁沿两侧传递到拱脚较稳定的结构上,从而减小由梁顶面直接传递的压应力与微型桩所承受的弯矩,这对微型桩结构的整体稳定性更加有利。
2.2 拱形排列微型桩受力情况分析
2.2.1 计算假定
计算基本假定:滑移面以上桩体看成是下端固定、顶端自由的悬臂桩,微型桩所承受的滑坡推力假设为均布荷载,令其值为q[6]。微型桩与顶梁的连接为固定连接,桩顶沿连系梁径向移动不考虑切向位移。
2.2.2 拱形连续梁内力情况
拱形连系梁可简化为拱轴线在水平面内,拱轴作用有多余约束的高次超静定无铰拱。本文考虑连系梁与微型桩顶之间剪力,同时还考虑相互作用时连系梁的弯矩与扭矩,连系梁跨度为l。为便于分析连系梁内力,建立如图2所示整体坐标系xyz,和局部坐标系x′y′z′。其中,整体坐标系xyz原点O位于最左端微型桩顶,x轴为水平布置左右两端微型桩的连线,向右为正;局部坐标系x′y′z′原点M为拱形连系梁上的任意一点,x′轴沿连系梁法向方向,y′轴沿拱形连系梁切向。以指向右端为正。
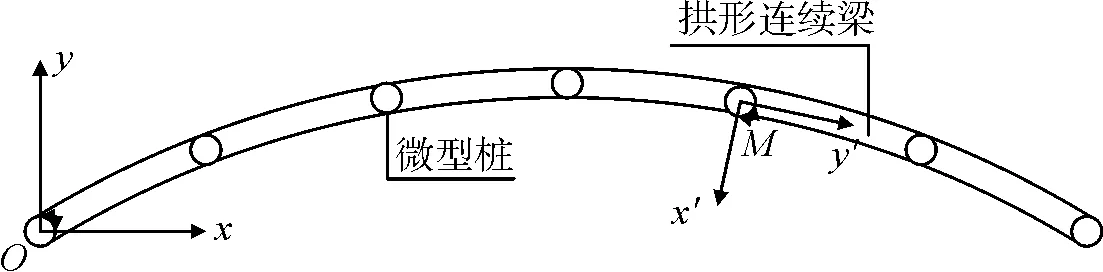
图2 整体坐标系和局部坐标系示意


(1)
2.3 微型桩内力及位移计算

(2)
2.4 力法柔度方程
(3)
3 算 例
3.1 模型建立与参数选取
某滑坡滑动面以上为硬塑性黏土,内摩擦角φ=20°滑面以上取m=5 000 kN/m4,滑面以下取k=40 000 kN/m3。桩h=12.6 m,受荷段h1=6.1 m,锚固段h2=6.5 m,桩顶连系梁跨度l=8.2 m,设桩处滑坡推力q=302 kN/m,桩间距沿跨度方向为1.2 m,滑坡推力按三角形分布。单根微型桩采用3束φ32 的螺纹钢,孔径130 mm,桩与桩顶连系梁的弹性模量均为E= 2.6×107 kPa。计算上半部分时把桩体在滑面处视为固定端。两端抗力桩为0#与7#桩,其他抗滑桩编号为1#~6#桩,其中1#、2#桩分别与4#、5#桩对称布置,3#桩位于中间位置。
3.2 弧形连系梁内力分布情况
应用MATLAB程序分别计算矢跨比f/l= 1 /16、1 /14、1 /12、1 /10、1/6、1 /4时的连系梁内力图,计算结果见图3~图7。

图3 连系梁轴力

图4 连系梁剪力

图5 连系梁绕y′轴扭矩

图6 连系梁绕z′轴扭矩
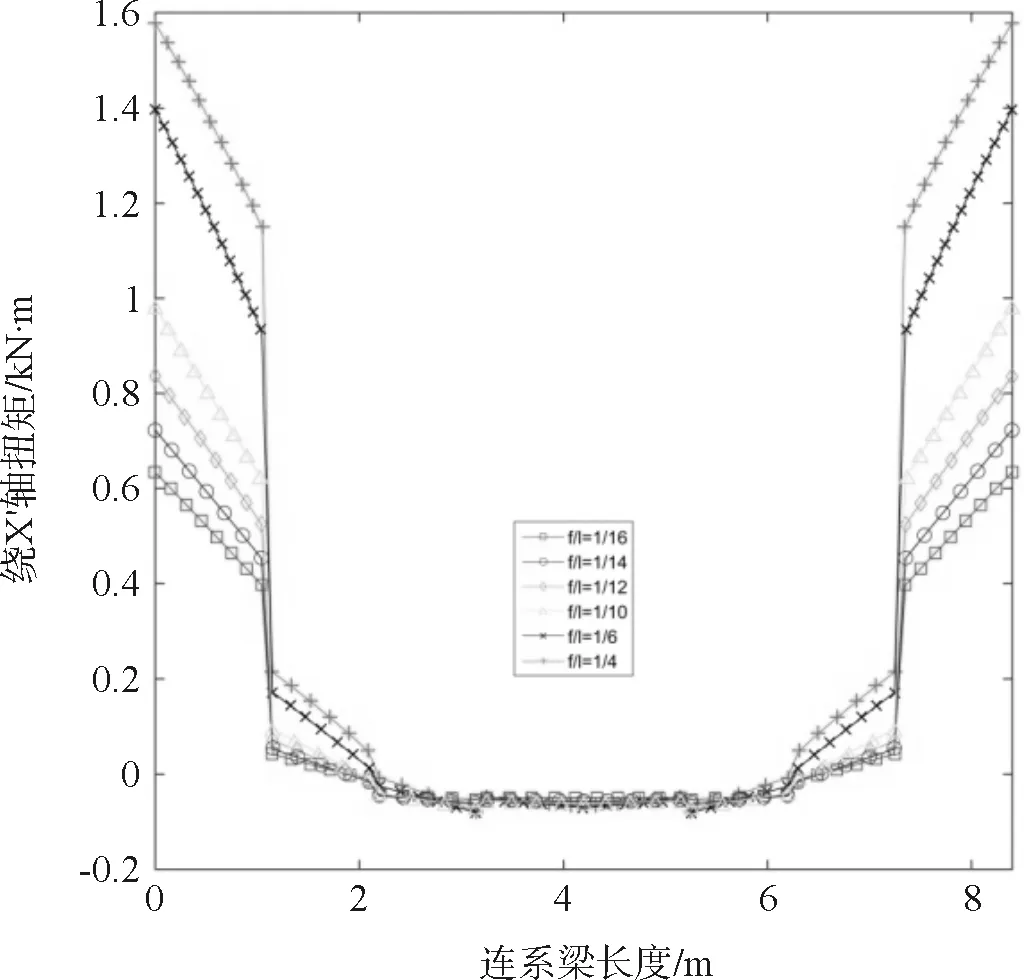
图7 连系梁绕x′轴扭矩
由图3可知,矢跨比较小时,随矢跨比增加连系梁轴力增加,当矢跨比达到f/l=1/12后,随矢跨比增加,轴力减小,且跨中部分减小幅度较大;由图4可知,在桩顶处拱形连系梁剪力发生突变,随矢跨比增加,剪力减小且其分布趋于均匀。可以看出,在同一矢跨比下拱形连系梁轴力值较剪力值要更大,甚至达到数倍,这说明拱形连系梁主要承受轴向压力且受力较均匀,故用抗压性能好的混凝土刚性连系梁来承受轴向压力,充分发挥受压构件的作用。
由图5~图7可知,拱形连系梁绕y′轴扭矩在两端呈现最大数值,中部则趋近于0,随矢跨比增加,扭矩数值整体呈减小趋势;拱形连系梁绕z′轴扭矩在两端较大,随矢跨比的增加,扭矩逐渐减小,端部扭矩减小明显;随矢跨比的增加,拱形连系梁绕x′轴弯矩增加,端部弯矩增加明显,但连系梁绕x′轴弯矩始终较小;总体来讲,连系梁x′轴弯矩较小,可忽略不计。当矢跨比增加时,拱形连系梁绕y′轴、z′轴的弯矩明显减小且分布更加均匀合理。
3.3 微型桩内力与位移特征
以2#桩为例,分别计算在不同矢跨比条件下,桩身在连系梁法向的内力及位移。

图8 微型桩剪力

图9 微型桩弯矩
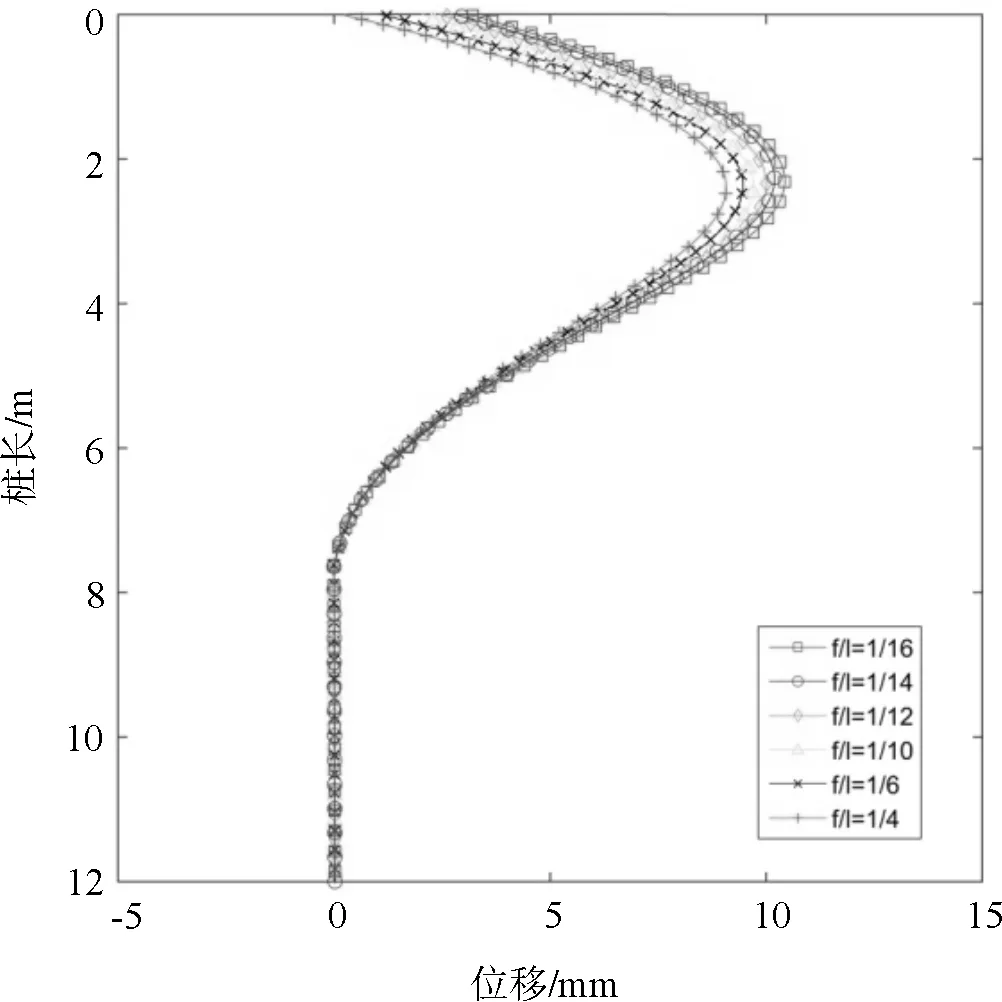
图10 连系梁位移
从图8、图9所示的微型桩内力变化趋势可以发现,桩顶连系梁对微型桩顶起到了约束作用,随矢跨比增大约束效果也得到加强,桩身沿法线方向剪力也随之增加,尤其在桩顶增加最大,但总体来讲矢跨比增加对剪力变化影响并不明显;同样的,在连系梁的约束作用下,桩身弯矩随矢跨比的增加而增加。
由图10可知,拱形连系梁对微型桩顶有较明显的约束作用,随矢跨比越大,桩顶以及桩身位移越小,约束效果也越明显。
需要指出的是,实况微型桩滑面处位移并不为0,因此,在计算桩体上半部分受力时把桩体在滑面处视为固定是不完全恰当的。此方法对微型桩的受力情况做出了偏安全的简化。内力计算结果偏于保守。考虑实际工程中微型桩桩体滑面处位移较小,为简便计算,故在此忽略不计。
4 结 论
(1)本文研究微型桩与拱形连系梁之间的剪力作用,推导了连系梁与微型桩内力与位移的计算公式,分析不同的矢跨比情况下的内力位移分布规律。
(2)拱形连系梁随矢跨比增加,剪力与弯矩均减小且趋于均匀;轴力值明显大于剪力值且在其f/l=1/12时出现最大值,使得连系梁所用混凝土材料抗压特性得到充分发挥。
(3)由于拱形排列微型桩顶部受到连系梁的约束作用,微型桩受荷段弯矩及剪力均有所增加,桩顶处最为明显。
(4)随连系梁矢跨比的增加,对桩顶位移的约束效果愈加明显,相应地,桩身各处位移随之减小。
5)拱形连系梁对微型桩起到约束作用,随连系梁矢跨比增加,约束作用越明显。这种布置形式能在一定程度上改善连系梁与微型桩的受力情况,使材料充分发挥作用,可运用于一些地形较为特殊的中小规模的滑坡治理工程中。
[1] 黄永勇. 微型桩处理滑坡的质量控制[J]. 铁道设计标准,2005(12):33-35.
[2] 龚健,陈仁朋,陈云敏,等. 微型桩原型水平荷载试验研究[J]. 岩石力学与工程学报,2004,23(20):3541-3546.
[3] 冯君,周德培,江南,等. 微型桩体系加固顺层岩质边坡的内力计算模式[J]. 岩石力学与工程学报,2006,25(2):284-288.
[4] 肖世国,鲜飞,王唤龙. 一种微型桩组合抗滑结构内力分析方法[J]. 岩土力学, 2010, 31(8): 2553-2559.
[5] 孙书伟,朱本珍,郑静. 基于极限抗力分析的微型桩群加固土质边坡设计方法[J].岩土工程学报,2010,32(11):1671-1677.
[6] 周德培,王唤龙,孙宏伟. 微型桩组合抗滑结构及其设计理论[J]. 岩石力学与工程学报, 2009, 28(7): 1353-1362.
[7] 肖维民. 微型桩结构体系抗滑机制研究[D]. 成都:西南交通大学,2008.
[8] 胡毅夫,王庭勇,马莉. 微型抗滑桩双排单桩与组合桩抗滑特性研究[J]. 岩石力学与工程学报, 2012, 31(7):1499-1505.
[9] 闫金凯,殷跃平,门玉明,等. 滑坡微型桩群桩加固工程模型试验研究[J]. 土木工程学报, 2011, 44(4): 120-128.
[10] 孙书伟,朱本珍,马惠民. 框架微型桩结构抗滑特性的模型试验研究[J]. 岩石力学与工程学报, 2010, 29(Z1):3039-3044.
[11] 白晨光,贾立宏,马金普,等.抗弯功能微型桩在基坑支护中的应用[J].岩土工程学报,2006,28(Z1):1656-1658.
[12] 朱本珍, 孙书伟, 郑静. 微型桩群加固堆积层滑坡原位试验研究[J]. 岩石力学与工程学报, 2011, 30(增1):2858-2864.
[13] 张志伟,邓荣贵,钟志彬.弧形排桩-连系梁抗滑结构加固隧道口滑坡应用研究及优化设计[J].铁道标准设计通讯,2014(11):108-113.
[14] 曾令录,林再星.铁道部第二勘测设计院. 抗滑桩设计与计算[M]. 北京:中国铁道出版社, 1983.
姚禹龙(1994~),男,本科,主要从事边坡稳定性研究。
TU473.1+2 U417.1
A
[定稿日期]2016-08-25
