对一道等效重力问题的拓展
2017-05-18景文成
景文成
(长春师范大学物理学院 吉林 长春 130021)
对一道等效重力问题的拓展
景文成
(长春师范大学物理学院 吉林 长春 130021)
从一道等效重力场的典型例题出发,通过延伸和拓展,挖掘其隐藏在问题背后的共性规律——等效重力观点.从而对解决复合场中同类问题起到一定的引导作用,提高解题效率.
等效重力 圆周运动 类平抛运动 类斜上抛运动
物体在多种场(重力场、匀强电场、磁场、浮力场等)中运动,将多种场的作用化多为一,用一个全新的“复合场”来研究物体的运动规律,可使研究的问题简洁灵动,这个复合场就是“等效重力场”.利用等效重力场的思想方法来处理问题,是一类常见而又颇有难度的问题.这类问题学生往往找不到突破口,受制于自身的思维而不得要领.在教学中教师通过典型问题为载体,进行针对性的延伸讲解,学生是能够受益匪浅并豁然开朗.
【典型例题】
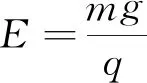
A.小球到达C点时对轨道压力为2mg
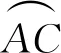
C.适当增大E,小球到达C点的速度可能为零
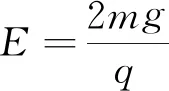
【答案】A,D.
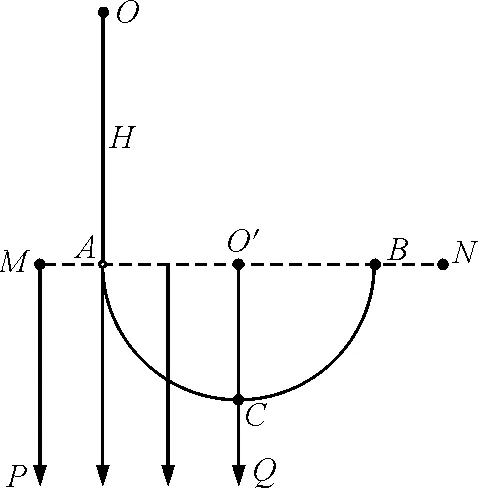
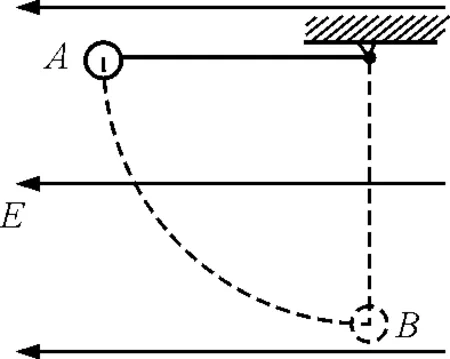
图1 例图
从这道题来看,如果借助等效重力场的方法,来解答会显得很简洁清晰,也会有助于学生以后能够利用等效重力的观点来解决问题,下面对每个选项进行分析(为了便于研究,等效重力用G′表示).
1 当qE=mg时,对小球由A→C→B过程的分析
从小球由A→C过程来看,由于电场力竖直向上,重力竖直向下,但是大小相等,所以等效重力为零,亦即等效重力不做功,弹力总指向圆心起到向心力的作用,可知由A→C为匀速圆周运动.因此可对O→C全程由动能定理列方程
解得
由于H=R,则
在C点由牛顿第二定律得
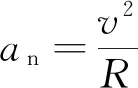
拓展
继续研究小球从C→B的运动,此时等效重力G′(等效重力为真正的重力)竖直向下,那么小球能上升多高?能否离开B点?
解析:
借助等效重力场的思想,由A→C等效重力不做功,只需比较H与R的关系即可.讨论如下.
(1)H>R时,小球从B点飞出做竖直上抛运动,如图2所示.
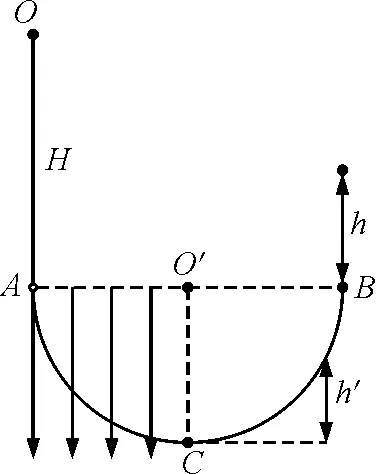
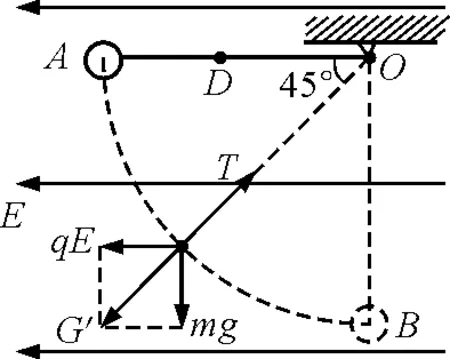
图2 借助等效重力场思想,分析带电小球在电场中运动
由动能定理有
mgH-mg(R+h)=0
解得
h=H-R
式中h为距B点的高度.
(2)H=R时,小球恰好到达B点速度为零.
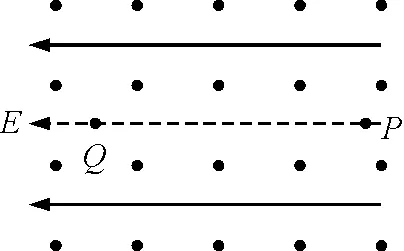
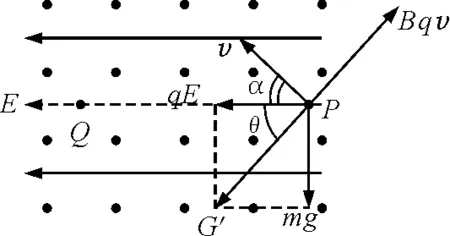
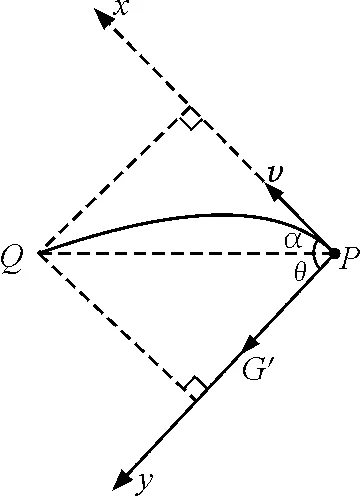
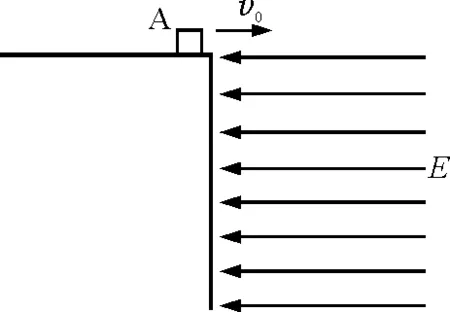
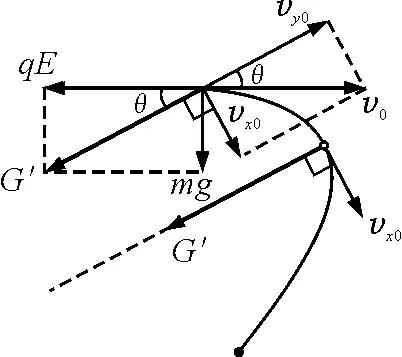
(3)H mgH-mgh′=0 解得 h′=H 式中h′为距C点的高度. 本题C选项, 适当增大E,由A→C过程得出qE>mg,两个力方向相反,等效重力G′=qE-mg,方向竖直向上,如图3所示. 图3 适当增加E,带电小球的受力分析 此时C点相当于竖直平面内重力场中的最高点,显然要过最高点满足 可知,在C点速度要求 所以C选项不正确. 本题的D选项,可知等效重力 G′=qE-mg=mg 方向竖直向上,小球刚好到达C点,列式如下 再由O→C全程动能定理得 联立可得 拓展 适当增大E(为某一确定值)此时等效重力G′=qE-mg,小球恰好过C点,H要满足什么条件? 解析: 进行受力分析如图4所示,计算如下 联立可得 讨论如下: 图4 适当增大E,小球恰好过C点 那么小球刚离开轨道F点时下降的高度(距A点)?计算如下. 设在F点刚好离开轨道,可知 等效重力为 G′=qE-mg 由O→F全程列动能定理可得 在F点刚要离开轨道,由等效重力G′沿半径方向分力提供向心力可得 由几何关系得 联立可得 式中h为AF间竖直高度. 适当减小E(为某一确定值),小球将怎样运动?减小E,可得出qE 分析可知,小球由A→C一直加速运动,一定能过C点.下面从高度H满足什么条件来延伸思考能否到达B点? 如果恰好到达B点的速度为零,此时可以看到A→C→B相当于只有电场力做功,因此由O→B动能定理全程列式可得 mgH-qER=0 由此可知 讨论如下: mg(H-h1)-qER=0 解得 mgH+(mg-qE)R-mgh2=0 解得 各种场力与重力不在同一直线上,物体可能做圆周运动、类平抛运动、类斜上抛运动等.此时可以把两个力进行合成当作等效重力G′来处理. 4.1 利用等效重力解决圆周运动问题 如图5所示,一个摆线长为l,质量为m的带正电摆球,悬挂在方向水平向左的匀强电场中.小球由水平位置A,从静止开始向下运动,且到达竖直位置时,速度恰好为零.求小球运动过程中,摆线受到的最大拉力. 图5 摆球为带正电的球体,单摆在电场中运动 小球从A运动到B,动能增量为零.因为摆线的拉力不做功,电场力(qE)对小球做的负功必定等于重力(mg)对小球做的正功,即 qEl=mgl 即 qE=mg 可见,小球受到的电场力与小球的重力大小相等,如图6所示,小球到达B后,将在A与B之间来回振动. 图6 单摆在电场中运动的受力分析 小球通过平衡位置时,绳的拉力大.根据类似机械能守恒,小球在平衡位置速度最大,且为 根据牛顿第二定律 所以,绳的最大拉力为 4.2 利用等效重力解决类平抛运动问题 (1)带电微粒运动速度的大小和方向? (2)若微粒运动到P点的时刻,突然将磁场撤去,那么经多少时间微粒到达Q点?(设PQ连线与电场方向平行) 图7 运动电荷在电场和磁场中运动 由于微粒做匀速直线运动,可知洛伦兹力与电场力和重力的合力(G′)平衡,如图8所示,θ为G′与水平方向的夹角,由于 所以 θ=30° 图8 洛沦兹力与电场力和重力的合力平衡 由平衡条件得 则微粒的速度大小为 与水平方向的夹角为 α=90°-θ=60° 磁场撤去后,微粒从P到Q做类似平抛运动,如图9所示,等效重力加速度为 图9 磁场撤去后微粒运动情况 在沿着v的方向有 x=vt 在垂直于v的方向有 又因为 所以运动时间为 4.3 利用等效重力解决类斜上抛运动问题 如图10所示,一带正电的小金属块A以初速度v0从光滑水平高台上飞出.已知在高台边缘的右侧足够大空间中存在水平向左的匀强电场,小金属块A所受电场力大小为其重力的2倍.则金属块运动过程的最小速度是多少? 图10 带正电小金属块从水平高台飞出 解法一:设经过t速度达到最小 在水平方向只受电场力作用做匀减速运动,加速度大小为 水平速度为 vx=v0-at=v0-2gt 在竖直方向做自由落体运动,竖直速度为 vy=gt 则金属块的速度 很明显借助函数求最值的方法很繁琐,不容易求解. 解法二:将金属块的电场力和重力合成为等效重力G′,设G′与qE间夹角为θ再将初速度v0分别沿着G′方向和垂直于G′方向分解(图11),则 vx0=v0sinθ vy0=v0cosθ 图11 利用等效重力求解类斜上抛运动 分析可知,在x轴方向一直做匀速直线运动,在y轴方向做匀减速直线运动,当vy=0时金属块在等效重力G′的最高点速度最小.因此可得 vmin=vx0=v0sinθ 而 所以 解法二是利用等效重力的观点解题,计算简洁思路清晰. 本文着重研究了在静电场与重力场中竖直方向上等效重力的问题,在教学中发现学生最不容易考虑竖直方向上的等效重力,所以本文进行了分析探讨.在另外的一些问题中会出现其他场力与重力不在同一直线上的情形,此时可以把两个力进行合成当作等效重力来处理,再利用牛顿定律解题时就看成一个力进行合成求得加速度;在利用动能定理解题时,直接利用等效重力的做功列方程,更能事半功倍提高解题效率. 1 王平杰.高中物理思想方法提炼与拓展.杭州:浙江大学出版社,2012.45~47 景文成(1978- ),男,在读硕士研究生,主要研究方向:课程与教学论(物理). 李春杰(1963- ),男,教授,主要研究方向:物理教育. 2016-11-07)2 适当增加E,等效重力方向竖直向上情况的分析
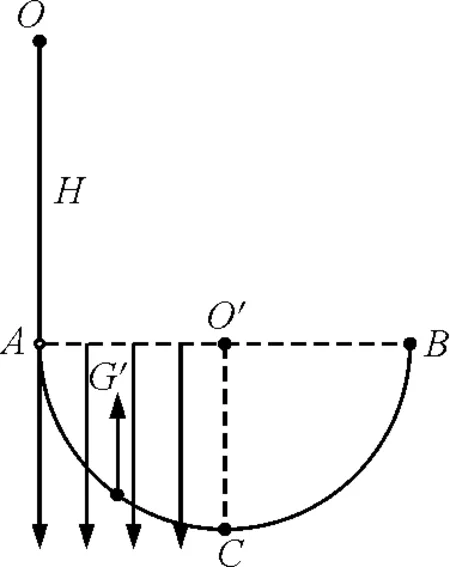
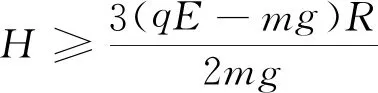
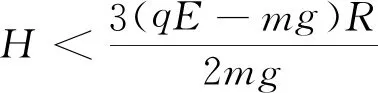
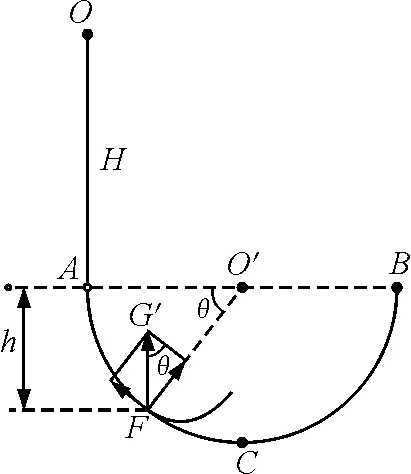
3 适当减小E,等效重力方向竖直向下情况的分析
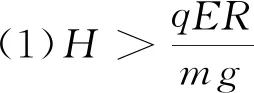
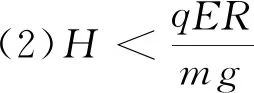
4 各种场力与重力不在同一直线上的情况的分析

5 小结
