基于递推滤波算法的卡尔曼滤波器在动态数据处理中的应用研究

黄小英

（福建水利电力职业技术学院，福建 永安 366000）

基于递推滤波算法的卡尔曼滤波器在动态数据处理中的应用研究

黄小英

（福建水利电力职业技术学院，福建 永安 366000）

文章介绍了一种基于递推滤波算法的卡尔曼滤波器，并对卡尔曼滤波器在对随机运动物体的位置估计——航天航空领域中的应用进行讨论，最后应用MATLAB软件对观测信号进行滤波仿真，给出计算机仿真结果，得到卡尔曼滤波器对消除观测噪声的作用。

递推滤波算法；卡尔曼滤波器；MATLAB

1 引言

数字卡尔曼滤波器是一种最优递归估计滤波器,它可以用于滤除一个附加在随机信号上的观测噪声，也可以预测一个动态模型的正确参数。如果给定初始条件，就能够预测这种模型的参数，并且能够随着每次新的观测对参数进行修正，给出估计误差的范围，卡尔曼滤波器是一个不断地预测、修正的递推过程,它对于测量噪声和模型噪声都具有非常好的效果，并且由于它具有便于计算机模拟的结构，使得卡尔曼滤波器在计算机跟踪设备中有广泛的应用，也就是说在某些情况下，卡尔曼滤波器的性能要优于其他的线性滤波器。

卡尔曼滤波器求解时不需要贮存大量的观测数据，并且当得到新的观测数据时，可随时算得新的参数滤波值，便于实时地处理观测结果，因此，卡尔曼滤波被越来越多地应用于动态数据处理中，尤其是GPS动态数据处理、惯性导航等。

2 卡尔曼滤波器的原理及算法

20世纪60年代初，随着空间技术发展对于处理统计特性具有非平稳性（即时变性）的多维随机信号和干扰的迫切需要，卡尔曼（R.E.Kalman）和布西（R.S. Bucy）提出了递推滤波算法。通过引入状态变量法建立反映被估计信号生成和演化机理的“消息模型”直接计算状态的估计值及其均方误差。实行递推算法和引出状态变量是卡尔曼滤波的两个明显特点。

卡尔曼滤波是由于维纳滤波在实际中遇到了困难而提出来的。维纳滤波的关键是求解维纳-霍夫方程，以期得到最佳线性滤波器的冲击响应。维纳滤波的模型如图1所示。

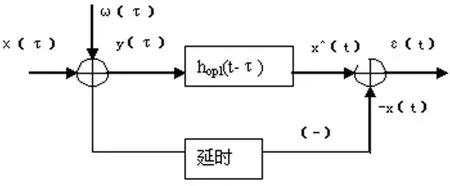
图1 维纳滤波模型

求解维纳-霍夫方程只有在平稳条件和有理谱密度情况下才是可行的。卡尔曼离开了维纳-霍夫方程，不去给出消息模型的协方差信息，而是给出了类似于动态线性系统的状态模型。由动态线性系统研究知，消息模型为：

式中x(t)为n维状态变量，u(t)为r维随机动态噪声，A(t)和B(t)为已知的随时间变化的n×n维和n×t维的矩阵。u(t)的意义需进一步说明，以免与下边将遇到的测量噪声ω(t)混淆。如果我们进行的是弹道估计，那么u(t)就是伴随信号的宽带扰动，它是伴随着x (t)一起到来的，是由随机牵引、引力不确定等因素决定的。u(t)与x(t)的初始值x(t0)是不相关的。卡尔曼假设的测量模型：

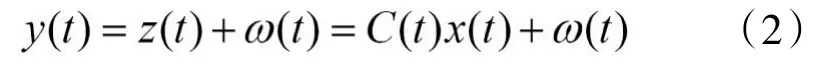
式中z(t)为m维测量变量，ω(t)为s维随机测量噪声，C(t)为已知的随时间变化的m×n维矩阵。测量噪声ω(t)是在测量过程中引入的。

下面为滤波过程。假设随机动态噪声u(t)与测量噪声ω(t)均为零均值白噪声，则

式中U(t)为r×r维非负定阵，W(t)为s×s维非负定阵，δ(t-τ)为狄拉克函数。用δ(t-τ)描述u(t)或ω (t)的协方差函数是数学上的理想化，因为δ(t-τ)是物理不可实现的，而自然界中严格的白噪声也是不存在的，但是它是许多噪声的一种近似。在此基础上，卡尔曼给出了滤波模型：

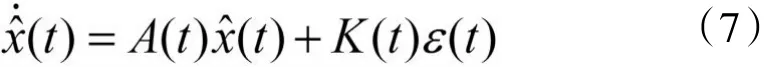
式中

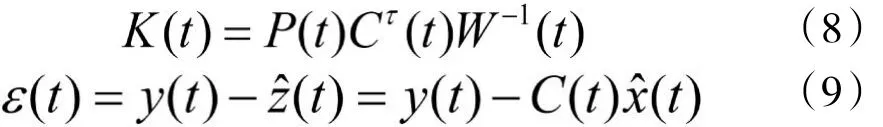
所以式(7)可以写为

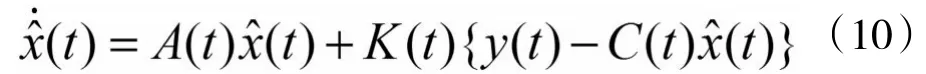
称K(t)为增益矩阵，P(t)为状态估计中的误差协方差阵。P(t)是下述微分方程式的唯一的解：

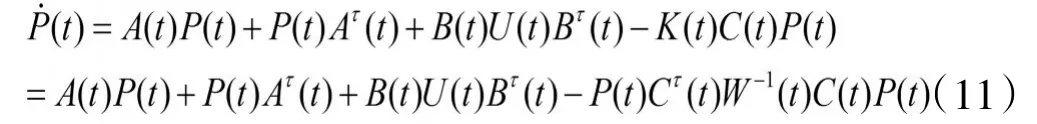
这是一个非线性方程，是著名的黎卡蒂方程。

图2是卡尔曼滤波器的结构图。它是由式（1）所示的消息模型、式（2）所示的测量模型及式（10）的滤波模型所组成的。

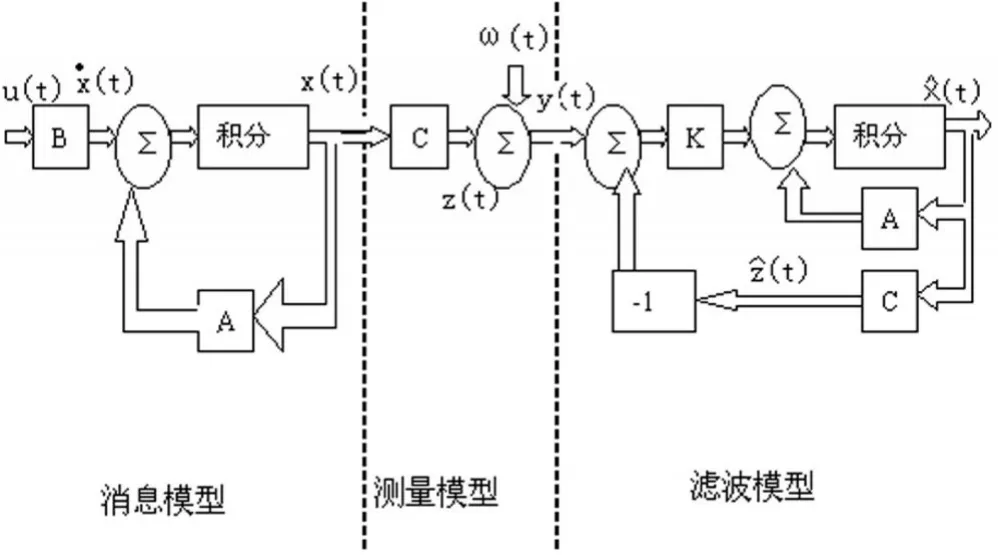
图2 卡尔曼滤波器模型

3 卡尔曼滤波器对随机运动物体的位置估计的应用研究

假设某一系统为一架航天飞机，从它的推进器喷射出的气体燃料的燃烧对于火箭的推进作用是一个随机过程，而推进器带有一个反馈控制系统。航空控制中心检测和预测航天飞机的运行轨迹从而对航天飞机进行控制需要用到数字卡尔曼滤波器。为了用数字卡尔曼滤波器消除信号中的噪声，被测量的进程必须能用线性系统描述。

例如飞行中的航天飞机，其状态由航天飞机的方位P和速度V构成。输入u是控制加速度，而输出y则是测量位置。假定每隔T秒都能改变加速度并测量飞机的方位，根据物理学基本定律，速度V将由下述方程描述：

因此，下一时刻（T秒之后）的速度将等于当前速度加上控制加速度与T的乘积，实际上该速度将受到风及其它意外噪声的干扰。这些速度噪声是随时间变化的随机变量，因此下述方程能更好地反映V的实际情况：

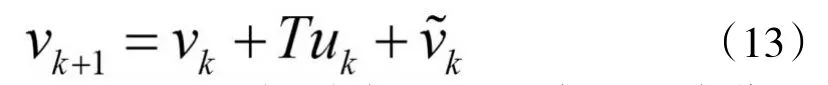
其中 表示速度噪声。类似地，可以推导出方位P的方程：

矢量X包含了系统状态的所有信息，但是它却是我们无法直接测量得到的。我们已知测量输出应该等于飞机的方位值，所以我们用矢量X代替上面的P和V，从而可以得到线性系统的状态方程如下：

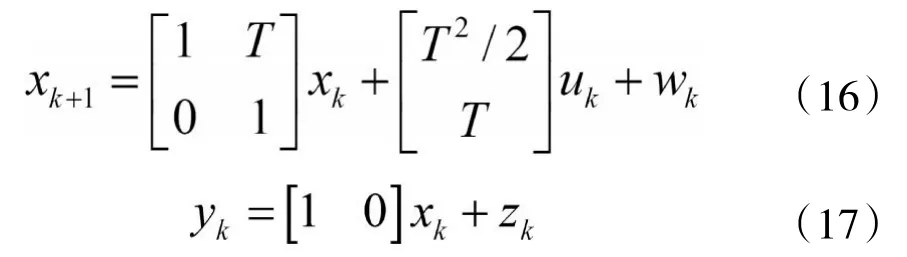
其中，zk表示测量仪器的原因产生的测量噪声。

我们的目的是根据对系统行为的认识和测量值，能最好的估计未来的航天飞机的方位和速度，即矢量X，从而通过反馈系统来对航天飞机的方位进行调整和控制。从系统的方程我们可以知道系统的行为，但是要怎么样才能决定哪种估计才是对系统变化的最优估计？当然不能仅仅依靠我们的观测数据，因为其中包含有非常大的测量噪声。卡尔曼滤波器正是状态估计的有效工具。

卡尔曼滤波器方程有很多公式表达方法，选择其中一种，表述如下：

上面的四个方程，每个方程都包含矩阵运算。在上述方程中，上标-1表示矩阵求逆，上标T表示矩阵转置。S表示观测值的协方差矩阵，K矩阵称为卡尔曼增益矩阵，而P矩阵为预测误差的协方差矩阵。

卡尔曼滤波算法的一个重要特点是递推性，它工作在“预测-修正”的方式中，即把修正项加到预测的估计值中去，最后得到滤波后的估计值。因此，上述状态估计方程相当直观。方程中用来推导k+1时刻状态估计值的第一项等于A与k时刻状态估计的乘积。如果没有测量噪声的话，这一项就是状态的估计值。换句话说，状态估计可以像系统模型中的状态向量一样传送至后续时刻。方程中第二项为修正项，代表在我们的测量条件下，要怎样校正对传送的状态估计进行修正。方程中，Kk表示增益矩阵。Kk表示新的测量值作用的大小。K方程表明：如果测量噪声远小于过程噪声，Kk将很大，也就是说当Kk较大时，新的量测值的作用就大，对预测的估计值的修正就大；反之就表明预测的估计值比较准确，也就是表明测量噪声远大于过程噪声。

4 计算机仿真及结果

我们在计算机上使用MATLAB来仿真式(13)和式（14）所描述的具有由随机喷发所带来的加速度的动态系统，并用数字卡尔曼滤波器对测量到的信号进行滤波。

假设我们所测量的航天飞机的方位与其实际方位相比具有10英尺的误差，即方位测量的误差为10英尺。又令其加速度具有0.5英尺/平方秒的标准偏差或者称为加速度噪声（accelnoise）。方位测量的周期为0.1秒（T=0.1）。

因为T=0.1，系统的线性模型可表示如下：

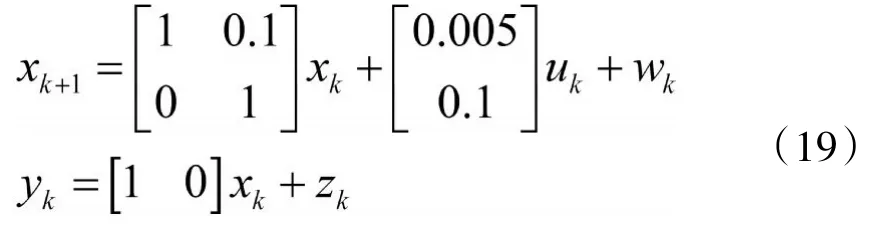
由于我们假设了测量噪声具有10英尺的标准偏差，所以测量噪声的协方差矩阵Sz就等于100。此外，我们还需要推导出过程噪声的协方差矩阵。根据假设，我们可用下式来求出过程噪声的协方差矩阵。

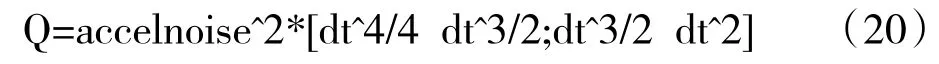
其中，^表示幂运算，dt为测量时间间隔，即dt=0. 1。假设整个过程持续了50秒。我们使用MATLAB软件来进行仿真，仿真以后可以非常清楚的看到，尽管存在非常大的测量噪声，但是仍然可以使用卡尔曼滤波器来比较准确的估计出航天飞机的正确位置。下图3到图6是仿真的结果。

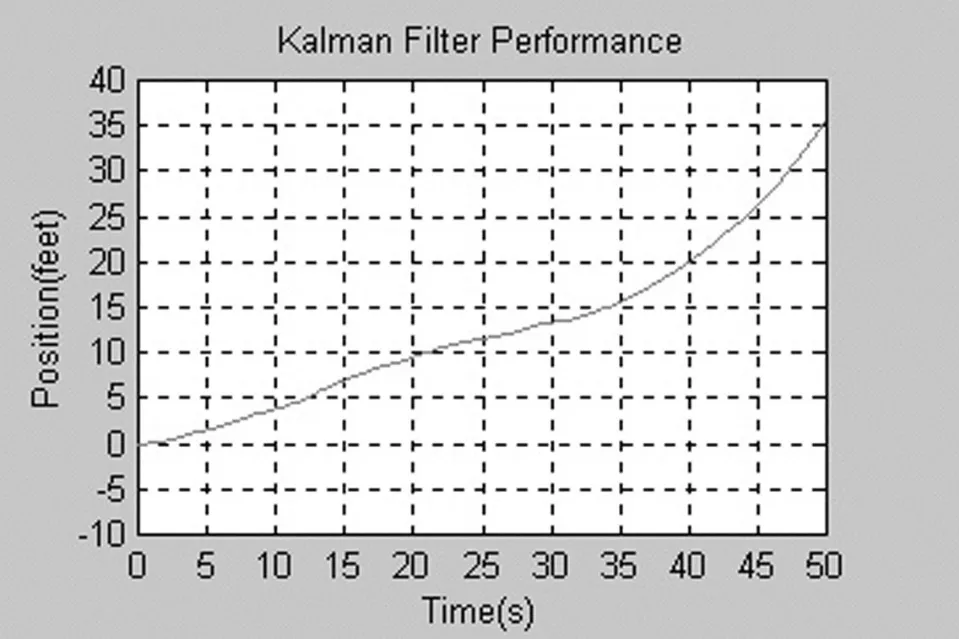
图3 航天飞机实际方位轨迹

图4 航天飞机的测量方位轨迹

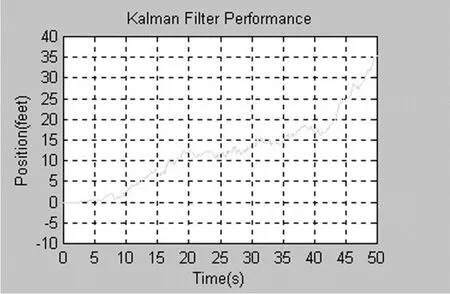
图5 卡尔曼滤波后的估计方位轨迹

图6 预测值与实际值以及测量值的对比

从图4我们可以看到方位曲线混有非常大的噪声，图5是如图4所示的信号经卡尔曼滤波之后的航天飞机方位轨迹的估计值曲线。在图6我们可以更清楚的对比一下估计值曲线于实际方位曲线之间的误差，可以发现卡尔曼滤波器可以比较好的滤除混杂在信号中的噪声。

由上图结果可以看出：在线性系统中，尽管系统的观测值和实际值相差较大，但卡尔曼滤波系统却能较好的估计出下一时刻的位置。而且误差和协方差较小，证明了卡尔曼滤波器在预测估计方面的有效性。

5 结论

卡尔曼滤波对消除观测噪声的作用是很明显的。目前，在许多实际控制系统中都采用计算机进行实时处理，在采样过程中，必然带进许多观测噪声。卡尔曼滤波器求解时不需要贮存大量的观测数据，并且当得到新的观测数据时，可随时算得新的参数滤波值，便于实时地处理观测结果，因此，卡尔曼滤波被越来越多地应用于动态数据处理中，尤其是GPS动态数据处理、惯性导航等。在核电站设备、人口统计建模、制造业、地层放射探测以及模糊逻辑和神经网络学等方面卡尔曼滤波器也具有很重要的作用。

[1]张有为编.维纳与卡尔曼滤波理论导论[M].北京：人民教育出版社，1980年7月.

[2][澳]B.D.O.安德森，J.B.摩尔著.卢伯英译.最佳滤波[M].北京：国防工业出版社，1983年12月.

[3][英]S.M.鲍齐克著.凌云旦译.数字滤波和卡尔曼滤波[M].北京：科学出版社1984年2月

[4]陈炳和著.随机信号处理[M].北京：国防工业出版社，1996年2月.

[5]徐宁寿著.随机信号估计与系统控制[M].北京：北京工业大学出版社，2001年1月.

[6]柏菁，刘建业，袁信.模糊自适应卡尔曼滤波技术研究[M].南京：航空航天大学，2001年9月.

Research on Application of Kalman Filter Based on Recursive Filtering Algorithm in Dynamic Data Processing

HUANG Xiao-ying
(Fujian College of Water Conservancy and Electric Power,Yong'an366000,Fujian)

In this paper,a Kalman filter based on recursive filtering algorithm is introduced,and the application of Kalman filter to the estimation of the position of random moving objects in aerospace field is discussed,at last,MATLAB is used to filter the observed signals,and the results of computer simulation are given to get the effect of Kalman filter on observation noise.

recursive filtering algorithm;Kalman filtering;MATLAB

TN91

A

1671-5004（2017）02-0007-04

2017-1-4

福建水利电力职业技术学院院级科研课题“切比雪夫微波带通滤波器的设计及仿真研究”（项目编号：XY1411C）

黄小英（1980-），女，汉族，福建省连城县人，福建水利电力职业技术学院信息工程系讲师，工程硕士，研究方向：电子与通信工程。