体型分析在观测服装号型适应性上的应用

邓椿山， 李 琴， 周 莉， 张龙琳

(1. 西南大学 纺织服装学院， 重庆 400715；2. 西南大学 重庆市生物质纤维材料与现代纺织工程技术研究中心， 重庆 400715)

体型分析在观测服装号型适应性上的应用

邓椿山1，2， 李 琴1，2， 周 莉1，2， 张龙琳1，2

(1. 西南大学 纺织服装学院， 重庆 400715；2. 西南大学 重庆市生物质纤维材料与现代纺织工程技术研究中心， 重庆 400715)

针对当前国内外缺失观测特定人群的服装号型适应性这一现状，提出以体型分析为基础的服装号型适应性观测方法，通过捕获人体的三维数据，从数据集群中选择服装号型分类变量的主成分，带入我国服装号型标准中进行验证。依据多组K均值聚类分布结果，结合验证后的号型覆盖率和档差关系选取最优K值，观测聚类中心的数值和分布图，描述该样本的服装号型适应性。结果表明：测量对象的差异性对号型分类变量的选取有直接影响，该服装号型适应性观测方法能够得到观测对象的体型发展趋势、服装号型覆盖率和档差调整方案、具体的“号”与“型”对应关系，提高了服装市场调研和生产计划的准确性。

体型分析； 服装号型； 适应性；K均值聚类

由我国国家标准化管理委员会和国家质量监督检验检疫总局发布的服装号型GB/T 1335.1—2008《服装号型 男子》，GB/T 1335.2—2008《服装号型 女子》和GB/T 1335.3—2008《服装号型 儿童》历经了1981年、1991年、1997年、2008年4个版本的修订。随着信息化在各行业的持续深入，我国服装号型的统计和分析工作面临着更高层次的要求。近几年内，非接触式三维扫描在服装学科应用的兴起，从手工测量向自动化、数字化转变的趋势越发明显，电子化量身定制(E-MTM)服装生产将成为服装业的重要发展方向[1-2]。

2001年英国设立了人体数据库SizeUK项目，是世界上首个采取人体扫描作为首要手段来获取测量数据的全国性人体尺寸调查[3]。近几年,随着人体扫描项目在我国的开展，基于体型分析的服装号型研究普遍通过控制部位的主成分分析得到分类变量数值，再利用K均值聚类法进行分类，对除身高外的其他数值的平均数进行档差计算[4-6]。此外，也有通过建立体型类别(基于控制部位的不同描述方法)与相应的数据段落，建立回归方程，反求体型分类[7-8]。以上2种正向与逆向的方法均涉及体型的分类判别模型，即形体指标的重要特征变量。Width-height独立评分方法则是在2个维度上分离相关性进行的人体体型探讨[9]。在过去的研究中，作为划分法的K均值聚类，利用循环定位技术将对象从一个划分移到另一个划分来帮助提高划分质量[10],K预设通常依据主观经验，后通过最优距离算法去判定K值。这种方法虽然在数值上能够推算出最优K值，但数值最优并不能代表此K值在观测意义上的准确性。

本文通过体型数据的分类变量推算，提出了以分类变量的档差情况结合K均值聚类分布图的离散程度逆向选取K值的方法。系统地整理了从体型数据收集到观测服装号型适应性的全流程，这种观测方法能够实际地描述K值的选择意义、观测对象的体型发展趋势、服装号型覆盖率、档差调整方案和具体的号与型的对应关系。

1 体型数据的获取与预处理

1.1 体型数据的获取

测量方法：依据GB/T 23698—2009《三维扫描人体测量方法的一般要求》，采用非接触式三维扫描(光栅法)捕获人体的点云数据，通过反求软件得到人体的三维视图。针对模型漏洞进行逆向修补，依据模型截面计算体型测量部位的围度长与高度数值，将数据录入相关分析软件(SPSS和MatLab)中进行体型数据集群的统计学分析和号型重组。

使用北京博维恒信科技发展公司的3D CaMega光学扫描仪(六探头)测量体型数据，人体点云数量约180万个，测量精度达到0.2 cm。

测量对象为西南地区在校女大学生，年龄范围为18～25岁。测量部位为身高、颈围、胸围、腰围、臀围、前腰节长、前胸宽、全臂长、后背长、肩宽、后背宽、前后腋间距、颈椎点高、上身长、下身长。

1.2 集群数据的预处理

1.2.1 样本量计算

在简单随机抽样的条件下，样本量n的计算公式为

式中：Z代表95%置信水平下的统计量为1.96；S为总体的标准差；d为样本允许误差。依据我国服装号型标准GB/T 1335.2—2008《服装号型 女子》规定的成年人体各部位尺寸的标准差和最大容许误差，以腰围为基础的样本量人数n最大为173人。为覆盖样本量并保证异常值的补录问题，选取191人(1.1n)为样本量进行测量。

1.2.2 异常值检查

对测量数据进行箱线图检查，在191个有效数据中剔除明显的异常值。剔除胸围异常值119号、28号进行重新测量，补录数据。

1.2.3 描述统计量

表1示出描述统计量，样本量n中数据胸腰差的极小值与极大值范围均超过国家标准的号型分档范围Y、C。

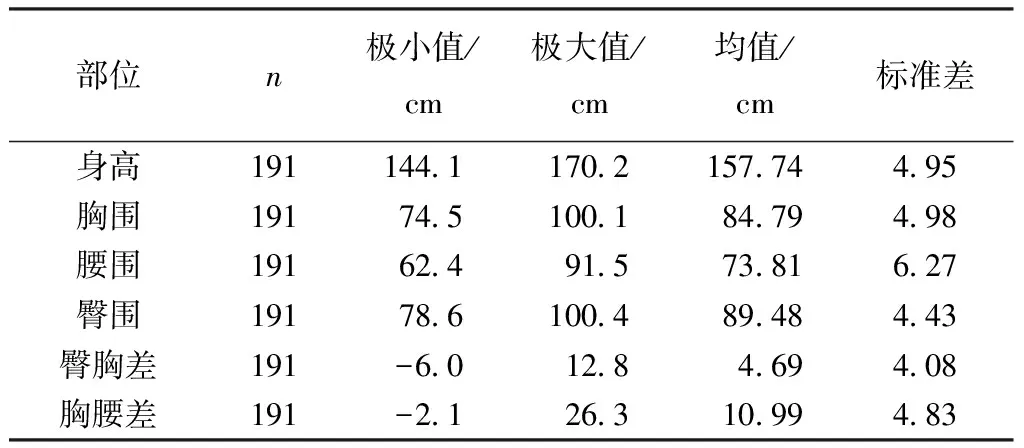
表1 描述统计量Tab.1 Descriptive statistics

2 与国家成年女性体型的对比

表2示出西南地区女大学生体型与国家统计成年女性的Z分数(Z>0，则观测值为增大趋势；Z<0，则观测值为减小趋势。可以看出，西南地区女大学生的身高、胸围、腰围均大于全国成年女性，且腰围增大明显，导致了胸腰差小于全国成年女性，偏胖体型趋势显著。臀围较全国成年女性相比较小，导致臀胸差的均值较小。

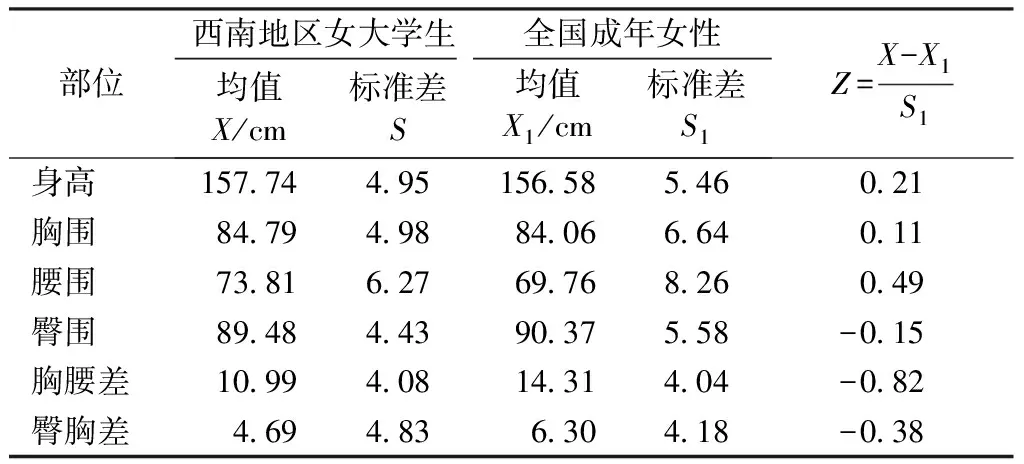
表2 样本女体与全国成年女体对比

3 服装号型分类变量分析

表3示出主成分矩阵。由表可知，体型主要的5个控制部位为：腰围、臀围、臀胸差、胸腰差、胸围。

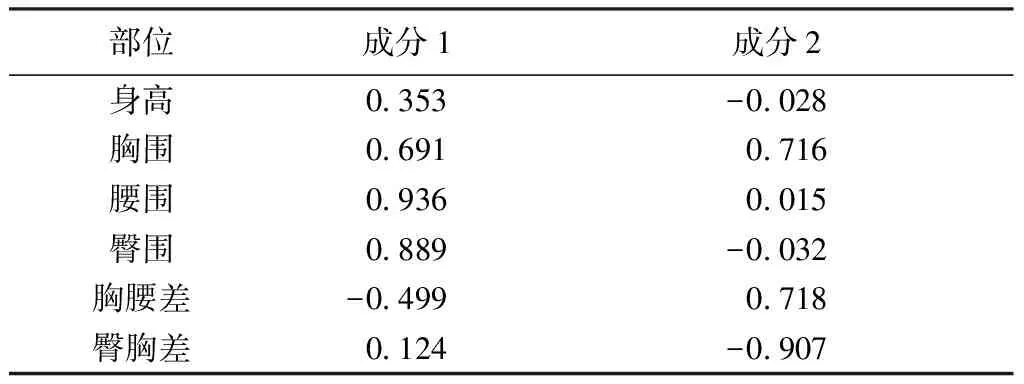
表3 主成分矩阵Tab.3 Principal component matrix

我国服装号型主要通过身高和胸腰差作为分类变量，包含Y、A、B、C这4种号型，如Y体型胸腰差范围为19～23 cm，并以4 cm为档差递减。表4示出在C体型(偏胖体型)4～8 cm的分档之外另有14组数据，为验证国家与国际服装号型在本文数据中的适应性情况，在国家服装号型标准基础上增加C2档(肥胖体型，胸腰差大于-2.1 cm且小于3 cm)，胸腰差极大值为26.3 cm仅1个案例，权重为0.5%，放入国标Y体型(19～23 cm)中进行统计。

ISO/TR 10652《德国服装标准尺寸系统》中女子体型是通过臀胸差作为分类变量，划分为H/M/A这3种号型。依据样本的臀胸差范围增加H2档，实验结果如表5所示。2组实验结果对比如表6所示，综合6项身体部位均值差可得：以胸腰差作为分类变量，在身高、腰围及臀胸差上的离散度较好；以臀胸差作为分类变量，则胸围和臀围的离散度较好。由表3可知，腰围在体型中的权重较高，且身高、腰围及臀胸差的数据能更好地反映体型，所以选择胸腰差作为体型的分类变量。

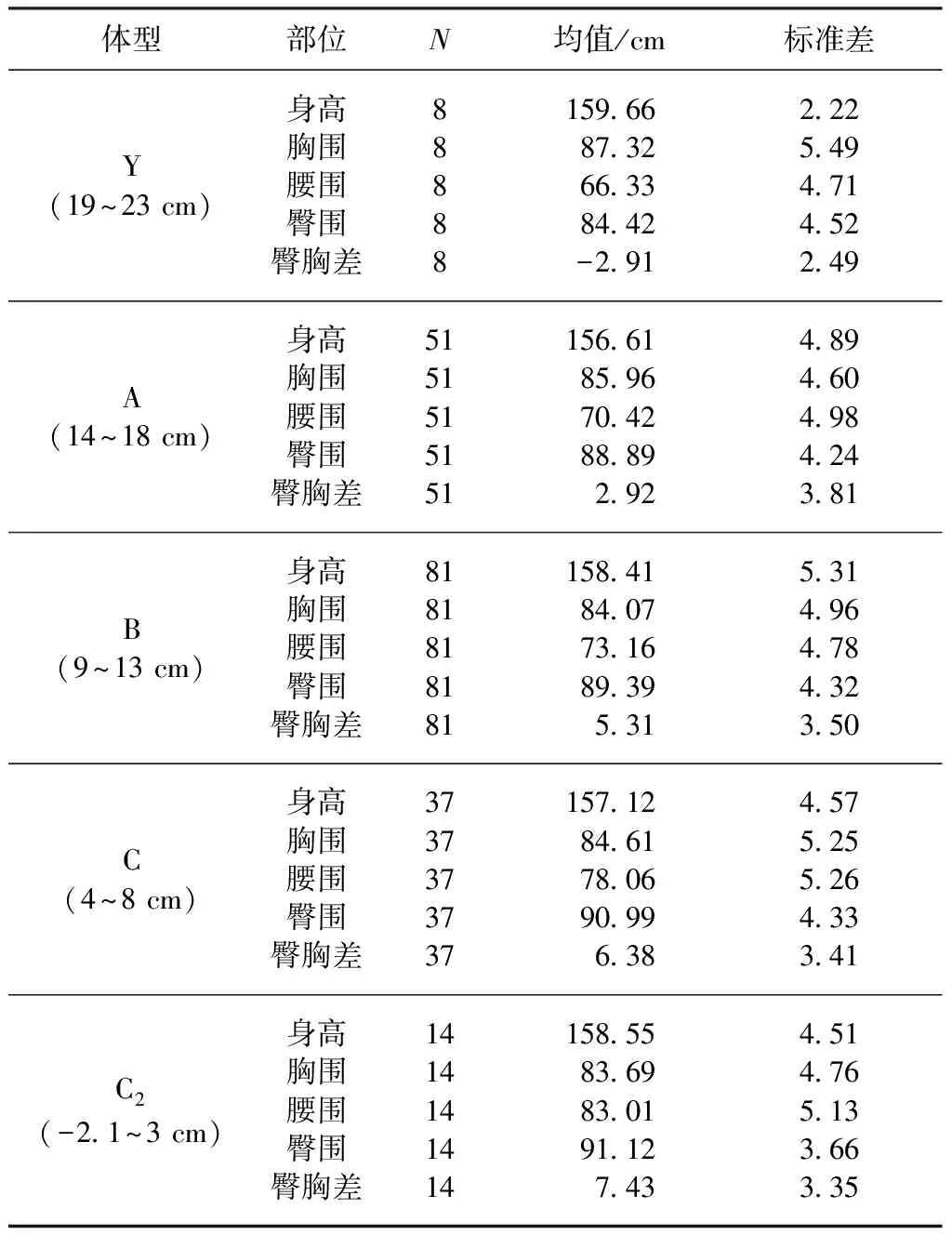
表4 胸腰差作为分类变量的实验结果Tab.4 Experimental results of chest-waist difference as classified variable

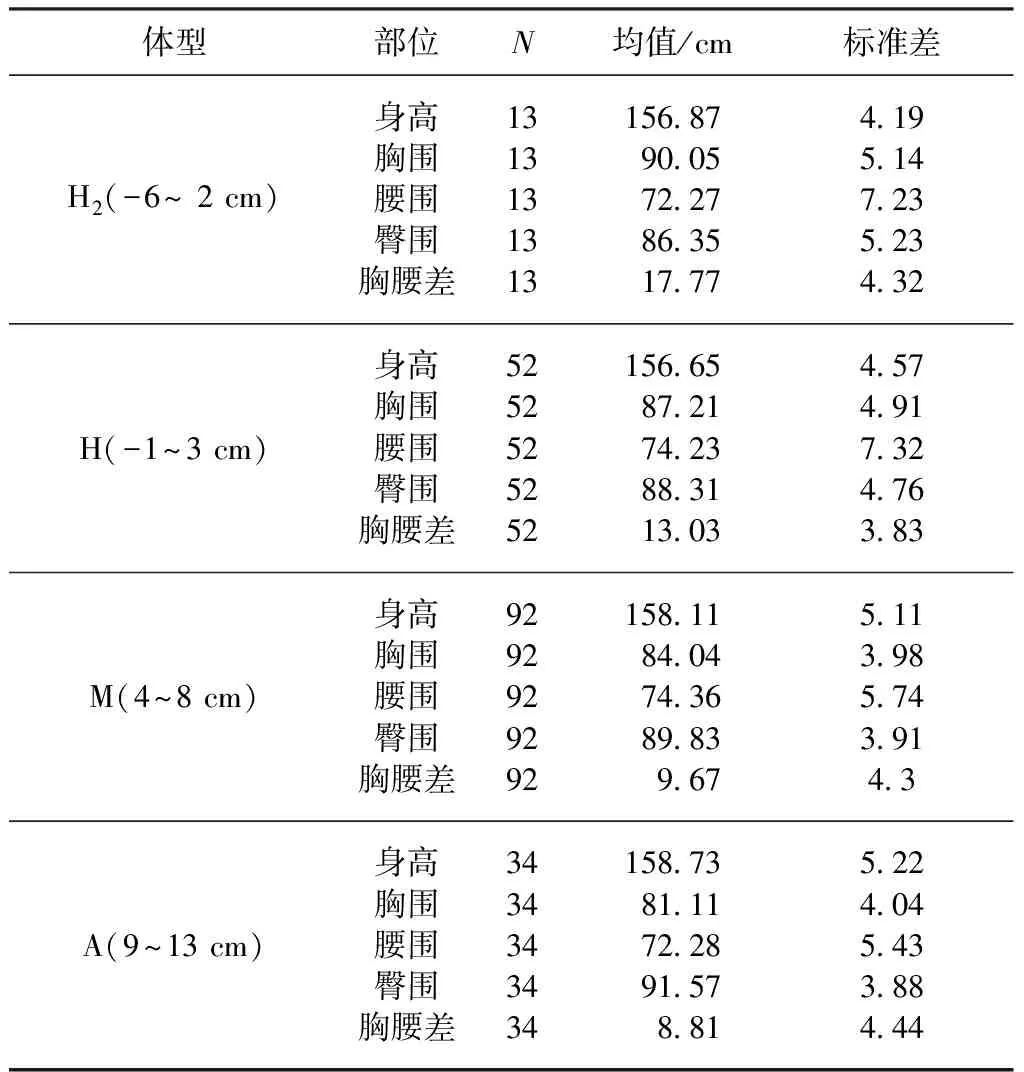
表5 臀胸差作为分类变量的实验结果Tab.5 Experimental results of hip-chest difference as classified variable

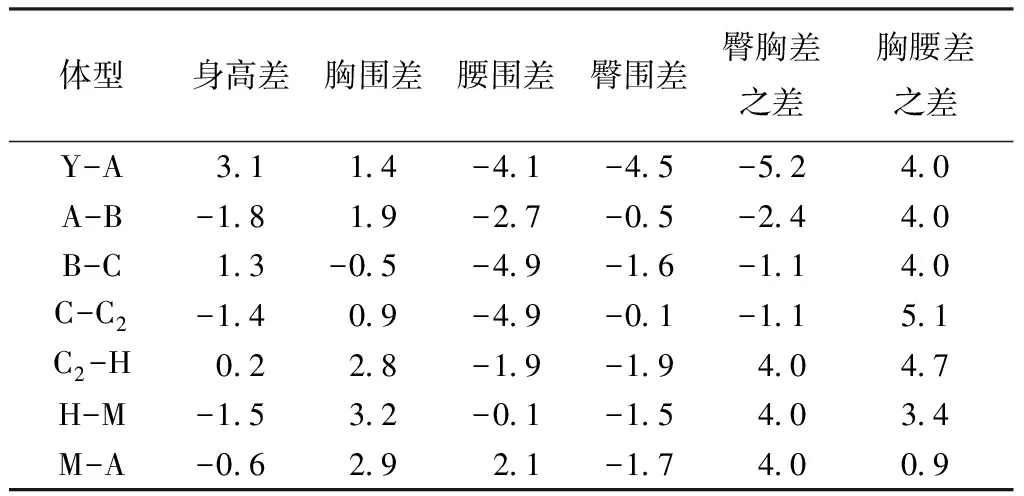
表6 2种实验结果对比Tab.6 Comparison of two experimental results cm

4 K均值聚类中心分析

由于K均值聚类法采用迭代计算方式，噪声和离群点对于聚类中心的结果有着严重的影响[11]，因此，在1.2.2小节首先对样本进行了异常值检查。

K均值聚类的算法公式为

聚类结果受初始聚类中心(k个代表点P1，P2，P3，……，PK)影响逐个对样本X进行分类，直至V点不发生变化。聚类收敛所需的迭代次数受数据离散程度影响[4]，迭代次数需要一定的数值保证样本量的循环计算，因此，迭代次数的选择需要根据样本量n的大小进行调整，以满足完全收敛。

本文选用MatLab 2014进行程序编译，选择K均值聚类对身高-胸腰差进行处理。K均值聚类需要在人工录入K值的前提下进行迭代计算，为能够清晰地观测到聚类中心的分布，需要通过K值的取值实验。调用MatLab中K均值聚类函数，选择迭代次数为10，计算K的最优整数取值(K≥4)，聚类分布图见图1、2。

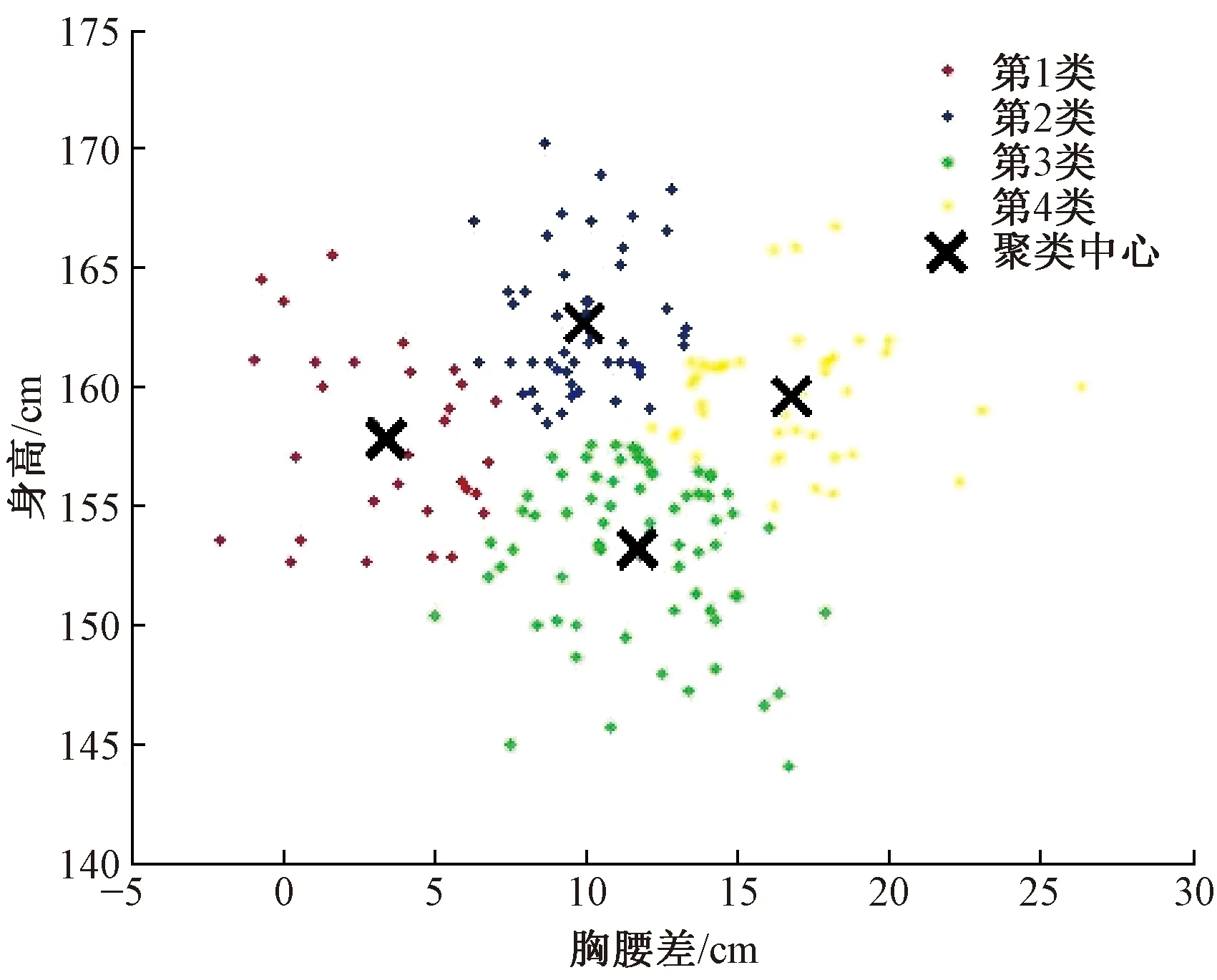
图1 K=4时K均值聚类分布图Fig.1 K-means cluster distribution map when K=4

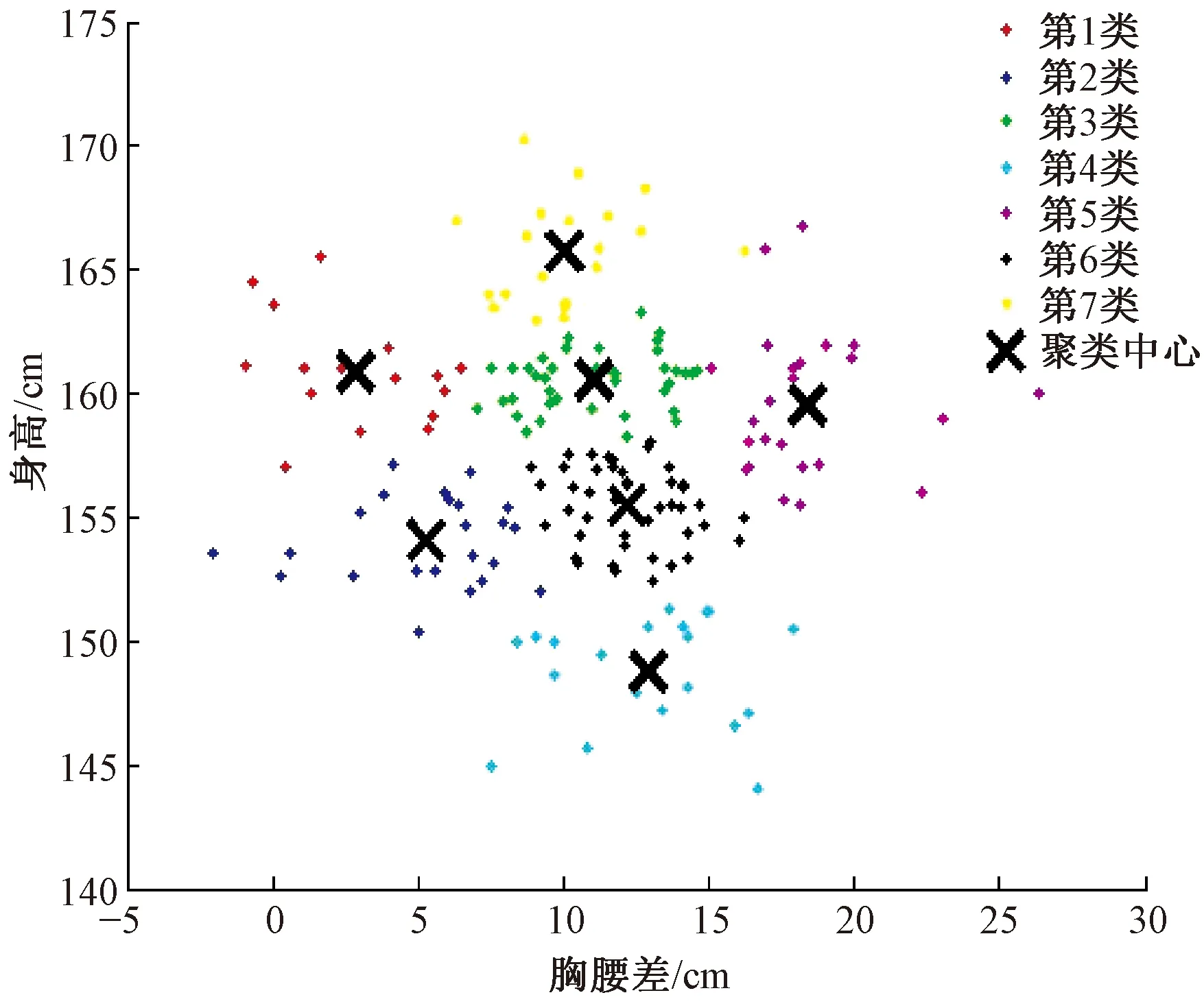
图2 K=7时K均值聚类分布图Fig.2 K-means cluster distribution map when K=7

由于篇幅的关系，本文截取了初始取值K=4，和最终取值K=7，2个聚类分布图逆向K值判定方法是基于服装号型实际运用情况，按照具有最大离散度的属性维对数据集进行排序划分。依据GB/T 1335.2—2008中的5.4档差数据对K均值聚类中心进行分析。K=4，第1类、第3类、第4类散点的分布过大，国家服装号型标准中身高以5 cm为档差，图中的聚类中心丢失了165～170 cm,145～150 cm的身高段，且离散度过高。K=5，身高分段未涵盖165～170 cm数据集群，且第1类数据的身高值范围。K=6，各类中胸腰差的档差分布较好，未能观测到165～170 cm所分布的散点。K=7，聚类结果较好，身高各档差均能观测到聚类中心，且胸腰差的分布档差较小易于观测。

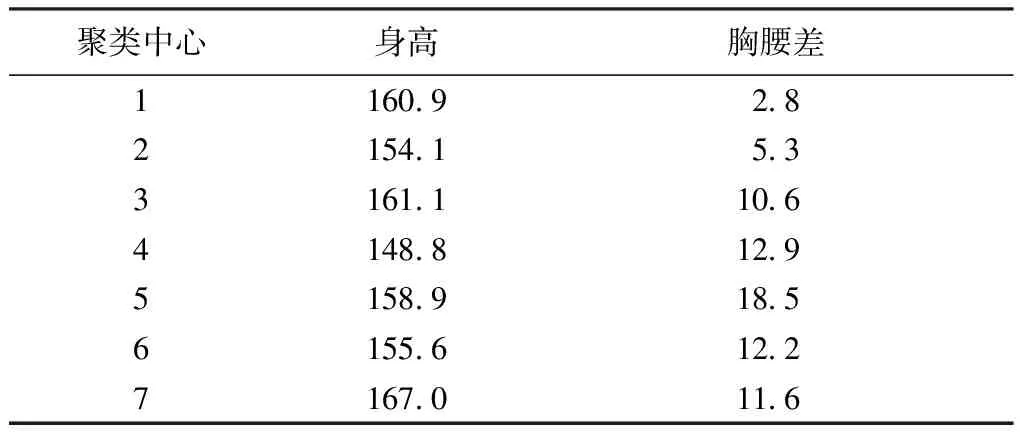
表7 K=7时聚类中心数值Tab.7 K=7 Clustering center values cm

结合聚类中心的数值和K=7的聚类分布图，观测到如下结果：

1)“号”分布的主要范围为145～170 cm，“型”分布的主要范围为-2～21 cm。

2)4类散点(3、4、6、7)的胸腰差集中于5～15 cm，即B/C(微胖、肥胖)体型，Y体型(偏瘦)阶段的人数较少。

3)身高范围在第2类、第3类之间(154.1～161.1 cm)，即身高区间为149～166 cm所对应的服装号型需求较为完善；身高高于166 cm的服装需求以B和C体型为主；身高低于149 cm的服装需求以A和B体型为主。

4)第7类散点表明聚类Y坐标中心167 cm， 身高在162～173 cm范围时胸腰差的聚类中心数值为11.56 cm，即B体型最多(同时涵盖部分A和C体型)。第1类、第3类、第5类说明身高的聚类中心(158.96～161.01 cm),身高在154～166 cm之间具有全部胸腰差的体型分类。第2类和第6类说明身高在149～160 cm区间体型主要分布在B和C区间。低于150 cm身高则主要聚类在A和B体型。

5 服装号型的适应性分析

根据对数据的处理、与国家成年女性标准的对比、K均值聚类分布图的观测，对西南地区在校女大学生的服装号型做如下调整。

1)使用“身高/胸腰差”作为分类变量针对西南地区在校女大学生仍然满足要求，但覆盖率需要增大(如C2)。

2)体型比例与2008年国家统计比对，结果见表8。体型向微胖、肥胖方向有发展趋势。因Y体型人数N=8，占比4.19%，在生产计划上需要减少。

表8 体型所占比重对比Tab.8 Contraction of body shape ratio %

3)身高范围在第2类、第3类之间(154.1～161.1 cm)，即149～166 cm的服装号型需求较为完善；身高高于166 cm的服装需求以B、C体型为主；身高低于149 cm的服装需求以A、B体型为主。

6 结 论

本文通过非接触式三维扫描设备捕获人体数据，经过数据预处理和主成分分析，将体型的主成分数据作为服装号型的分类变量进行验证。西南地区在校女大学生体型的集群数据验证结果显示，应以胸腰差作为体型分类的依据，与国家统计的全国成年女性数据比对后发现体型有向肥胖发展的趋势。使用K均值聚类分布图的离散情况和样本分类变量选取后的档差结合来看，在K=7时聚类分布为最佳观测值。针对样本人群需要加大服装号型的覆盖率，在产品计划上应减少Y体型的生产，服装号型的适应性在不同身高区间上有显著差异。FZXB

[1] 李晓久, 王玉秀, 刘皓. 非接触式人体测量系统中人体体型分类与自动判别[J].天津工业大学学报, 2007, 26(5): 34-35. LI Xiaojiu，WANG Yuxiu，LIU Hao. Classification and identification of body type in noncontacted body measurement system[J]. Journal of Tianjin Polytechnic University, 2007, 26(5): 34-35.

[2] SU Junqiang, LIU Guolian, XU Bugao. Development of individualized pattern prototype based on classification of body features[J].International Journal of Clothing Science and Technology, 2015, 27(6): 15-24.

[3] 刘咏梅, 张小雪, 郭云昕. 国内外服装用人体数据库调查与分析[J].纺织学报, 2015, 36(6): 143-144. LIU Yongmei, ZHANG Xiaoxue, GUO Yunxin. Survey and analysis on domestic and overseas human body database for garments′ use[J].Journal of Textile Research, 2015, 36(6): 143-144.

[4] 方方, 王子英. K-means聚类分析在人体体型分类中的应用[J].东华大学学报(自然科学版), 2014, 40(5): 594-598. FANG Fang, WANG Ziying. Application of K-means clustering analysis in the body shape classification[J]. Journal of Donghua University (Natural Science), 2014, 40(5): 594-598.

[5] 邹平, 吴世刚. 东北地区女青年体型及档差的修订[J].纺织学报, 2009, 30(11): 116-118. ZOU Ping, WU Shigang. Amendment of figure types and grading values of young women in China Northeast area[J].Journal of Textile Research, 2009, 30(11): 116-118.

[6] 尹玲, 张文斌, 徐才国. 基于有序样本最优分割法的女性体型分类[J]. 纺织学报, 2014, 39(9): 115-119. YIN Ling, ZHANG Wenbin, XU Caiguo. Female body shape classification based on optimal segmentation method for orderly samples[J].Journal of Textile Research, 2014, 39(9): 115-119.

[7] 谷林, 张欣. 基于聚类人体体型分类法的体型反算方法研究[J].西安工程大学学报, 2010, 24(1): 32-34. GU Lin, ZHANG Xin. The algorithm studies of human body′s shape classification based on cluster analy-sis[J].Journal of Xi′an Polytechnic University, 2010, 24(1): 32-34.

[8] 尹玲, 夏蕾, 许才国. 基于随机森林的女性体型判别[J]. 纺织学报, 2014, 35(5): 114-116. YIN Ling, XIA Lei, XU Caiguo. Female body shape prediction based on random forest[J].Journal of Textile Research, 2014, 35(5): 114-116.

[9] HAN Hyun Sook, KIM Sungmin, PARK Chang Kyu. Automatic custom pattern generation using width-height independent grading[J].International Journal of Clothing Science and Technology, 2015, 27(6): 1-12.

[10] 李惠君. 复杂仿真数据的降维与可视化聚类方法研究[D]. 秦皇岛: 燕山大学, 2013: 76-78. LI Huijun. Research on methods of complex simulationI data dimension reduction and visualization cluster-ing[D]. Qinhuangdao: Yanshan University, 2013: 76-78.

[11] 朱建宇. K均值算法研究及其应用[D]. 大连:大连理工大学, 2013: 15-17. ZHU Jianyu. Research and application of K-means algorithm[D]. Dalian: Dalian University of Technology, 2013: 15-17.

Application of body shape analysis in observation of clothing size adaptability

DENG Chunshan1,2, LI Qin1,2, ZHOU Li1,2, ZHANG Longlin1,2

(1.CollegeofTextileGarment,SouthwestUniversity,Chongqing400715,China; 2.ChongqingEngineeringTechnologyResearchCenterofBiomassFiberandModernTextile,SouthwestUniversity,Chongqing400715,China)

Considering the situation that effective observation of clothing size in particular groups was absent at home and abroad, observation of clothing size adaptability was proposed based on the body shape analysis. By tracing 3-D data of the human body, principal components of clothing size classification variables were selected from the data cluster and put into the national clothing size standard for validation. According to clustering distribution results of multiple sets ofK-means, the optimumKvalue was selected combining with verified clothing size coverage and variation relationship while the value and distribution of clustering center were observed so as to describe the sample clothing size adaptability. It is demonstrated that the differences between subjects have a direct effect on the selection of size classification variables so that this method can successfully get access to the body shape development trend of subjects, clothing size coverage and variation adjustment scheme as well as the corresponding relationship of size and ″shape″ so as to improve the accuracy of clothing market research and production plan.

body shape analysis; clothing size; adaptability;K-means clustering

10.13475/j.fzxb.20151005006

2015-10-23

2016-08-19

中央高校基本业务费专项资金资助项目(XDJK2015D025,XDJK2014A011)

邓椿山(1992—)，男，硕士生。主要研究方向为数字化设计。张龙琳，通信作者，E-mail: myfashionworks@163.com。

TS 941

A