替代定理的研究与应用

代广珍，王冠凌

替代定理的研究与应用

代广珍，王冠凌

（安徽工程大学电气工程学院，安徽芜湖241000）

替代定理是建立在已知电路中某二端子电路的端口电压和电流的基础之上，通过等效替代的方式来简化电路分析，为优化电路设计提供方便.现有电路分析教材中对替代定理的描述不足，导致存在争议.因此，对替代定理重新进行了描述，给出其各种形式及证明，并对争议进行了解释.最后，通过实例说明灵活运用替代定理进行电路分析，可以起到事半功倍的作用，从而有益于实际电路分析和电路理论教学.

替代定理；等效；电路

电路分析中关于等效替代的运用非常普遍，因而引起了广泛的关注与探讨.但是，仁者见仁智者见智，对某一方面的探讨难以覆盖全部，容易引起异议［1-2］.教材的编著者们一般都是基于各自的工程背景及应用需求，结合他们对电路分析课程的认识来编著教材的，因而必然存在着详略差异.目前，国内外高校使用的经典电路分析教材中对替代定理的阐述一般都比较简单［3-5］，甚至干脆没有［6］.然而，替代定理应用非常广泛，不仅可以对线性电路适用，还可以对非线性电路使用.由于在运用替代定理之前，必须要知道电路中被替代支路上的电压和电流，使得该定理应用受到限制.因此，对于替代定理的应用通常受到了人们的忽视.当前，我国高等教育在全面推进创新创业教育和自主创业工作的前提下，电路分析课程的课时被大幅压缩，教学大纲中对替代定理的要求也仅限于了解.然而，替代定理可以用来简化电路，使电路分析更为简单.尤其是对电路设计者而言，可运用替代定理优化电路设计.

本文针对关于替代定理存在的争议，在替代定理描述与电路表现形式及证明的基础上，给出了合理的解释，说明通用电路分析教材中对替代定理描述的不足，并对其应用进行了举例说明.

1存在的异议

文献［1］指出等效与替代是两个不同的概念，等效在任何情况下都可以和被替换的电路一样正常工作，然而替代则只能在特定情况下才能和被替换电路一样工作.从伏安特性曲线上比较等效和替代的关系，可以看出只有等效才能保证在任何情况下与原电路重合.最后文献［1］还指出密勒定理属于替代的范畴，并推广了密勒定理的形式.对此，文献［2］指出其否定了替代定理的内涵，并说明密勒变换改变电路拓扑结构，因而无从谈起密勒定理是替代的范畴.文献［6］也认为文献［1］中描述替代是只在一点满足被替代电路工作要求的等效，简单的说即替代是等效，这一说法不妥.

上述说法都具有一定的合理性，但也不能说哪一个就是完全正确的.为了便于阐明观点，结合文献［3-4］，首先给出了替代定理的描述、表现形式及证明.然后，对替代定理的本质进行了阐述.最后，通过对两个电路黑箱问题的求解，说明了替代定理的应用价值.

2替代定理的描述、表现形式及证明

2.1替代定理的描述

替代定理描述：图1（a）所示电路中，任意一端口连接的部分NB，都可以运用与该端口具有相同的电压u和电流i的电路元件或元件组合来替代.

文献［1］把替代与等效完全区分开来，因而与上述定理描述必然存在差异.的确，等效并不需要考虑被替换部分端口的电压和电流，即端口电压和电流必须为唯一解的情况，如运用戴维宁定理对含源线性网络进行的等效，不论外接负载如何变化，等效对含源线性网络都满足.而替代必须要使得端口电压和电流具有唯一解，否则就不能满足.但是过分的区分概念，会使得概念过于繁多，而纠结于过多的概念术语又会增加教学过程中学生学习的负担.从伏安特性曲线上不难看出，等效与被替换电路两者完全重合，替代与被替换电路相较于一点.为此，把两者结合在一起统称为等效替代，把替代作为其中的特例，不仅使得概念简洁，也可以减轻教学负担.此外该描述更贴合实际应用，可以有多种选择.

图1原电路及替代定理的表现形式

2.2替代定理的表现形式

针对上述定理的描述，给出了下列关于定理的表现形式，如图1（b）至（f）所示.图1（b）中运用电压源us替代NB，且us=u，该替代形式主要是利用了电压源上流过的电流受外电路确定，也即电压源上的电流受NA确定.图1（c）中运用电流源is替代NB，且is=i，该替代形式主要是利用了电流源上流过的电压受外电路确定，也即电流源上的电压受NA确定.图1（d）中运用电阻R替代NB，R的大小为，也即R上的电压和电流都是由NA确定.图1（e）和（f）中分别运用了电压源和电流源与电阻的组合替代NB，（e）中R分得的电压大小为u-u，故i=有；（f）中的R分得的电流大小为i-i，故有u=.

ss

2.3替代定理的证明

对于定理的证明，文献［3］已经对图1中（b）和（c）两种形式的证明进行了阐述（.d）形式中，由于，用替代后不改变端口特性，故自动获证（.e）和（f）两种形式的证明也可以采用文献［1］中对（b）和（c）的证明方法，本文用图2给出了（e）的证明过程.

在NB的端子d与a之间串接两个极性相反的电压源us和电阻R组合，由于极性相反，不影响原电路的特性.显然，串接的两个电阻R上的电压也相互抵消，不防设结点c左边的电阻R上分得的电压为u-us，则结点c右边的电阻R分得的电压为us-u.这样结点c与b的电压为0，于是可以用一条导线将c、b短接，如图2中虚线所示，从而将NB替代为电压源us和电阻R组合.因为（f）是（e）的对偶结构，因此（f）也成立，可以用类似的方法证明.

图2替代定理的证明

2.4替代定理的本质

替代定理的本质直观地理解，就是用电路中一个端口所具有的电量大小的元件或元件组合替代该端口连接的部分，替代后不改变端口的拓扑结构，因而也就不改变KCL和KVL方程.这就相当于对于给定的一组线性（或非线性）代数方程，只要存在唯一解，则如果用解去替代其中任何一个未知量，方程两边相等，即替代后不会引起其它变量解的改变.

需要注意的是，替代前后必须保持电路解的唯一性，至于被替代部分是否有源，抑或是否包含受控源或是其控制量，都无关紧要［7］.考虑到电路分析教材中对替代定理的描述过于简单，文献［8］对含受控源电路如何应用替代定理做了补充，文献［9］也提出了运用转移控制量的方法来运用替代定理.

3替代定理的应用

替代定理在简化电路分析、方便电路计算、优化集成电路设计方面，作用尤为明显.为说明这一点，以电路黑箱问题为例来说明其应用.

例1图3的（a）和(b)中，NR为互易网络，试求：图3（b）中的电流I1［6］.

为计算方便，将图3（a）中的1 A电流源用2 A电流源和1 Ω电阻并联替代，如图4所示.此时应确保图3（a）中端口1-1’上的电压和电流不变，即仍有1 A电流流入且电压为U1=2 V，而文献［6］中将替代后电路与原题图（b）中的端口1-1’上的电压都标为UR，造成与后面的分析产生误解.比较替代后电路和图3（b），发现将2 Ω电阻和NR组合在一起依然是一个线性互易网络，采用互易定理的第二种形式，可以写出式：2 A×UR=1 A×U2，得UR=0.5 V，于是得到I1=UR/2 Ω=0.25 A.图5中l2是替换后电路端口1-1’上的电压与电流之间的关系曲线，与原电路曲线l1相较于Q点.

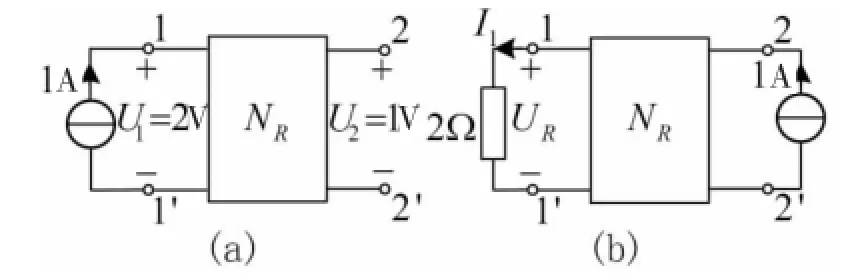
图3例1电路

图4替代后电路

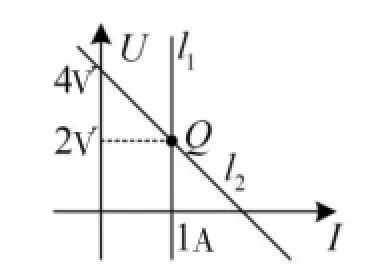
图5端口1-1’伏安特性

显然，图5伏安特性曲线不重合，属于文献［1］中严格意义上的替代.然而，教材［3］中只是将替代定理描述为图1中的（b）、（c）和（d）三种形式，因而存在描述上的不足.替代是在交点处等效，其实是完全一致.因此，对于教学来讲，将替代单独划分开来没有必要，反而使得教学负担加重.例1说明了将电流源替换为电流源与电阻的组合，并将电阻包含在黑箱当中，可以方便电路的分析和求解.

例2线性时不变电阻网络如图6（a），已知us=5cosωt V，RL=10 Ω时，uL=2+2cosωt V；us=2 V，RL=5 Ω时，uL=2%V，则us=5 V，RL=20 Ω，负载电压uL是多少？

根据例2电路和已知条件，直接运用电路知识难以求解.不妨将电阻RL用电流大小为iL=uL/RL的电流源替代，如图6（b）.根据叠加原理，可以将RL上的电压uL用电压源us、网络N和电流源iL三者单独作用再叠加来表示.设A、B、C分别表示三者对uL贡献权值，则可得：uL=Aus+Bus+CiL.由于网络N不变，对uL的贡献也不变，不妨设uN=1.根据题目的已知条件可列出下列方程组：

图6例2电路

求解得到：A=0.5、B=2、C=-2.5，代入式5A+B+CuL/20=uL，即可求出uL=4 V.

在例2的分析求解过程中，通过合理的替代，使的原本难以求解的题目，变得简单易于求解.此外，可以运用替代定理将非线性电路转化为线性电路，将非线性量转化为线性电路中的变量，从而建立响应与变量之间的关系［10］.

4结语

电路分析教材中关于替代定理的描述，因存在不足而引起争议.在对替代定理重新描述后，给出了各种表现形式以及相应的证明，并对存在的争议作出了合理的解释.通过举例说明了没必要过分细化替代与等效，且灵活运用替代定理对于电路黑箱问题进行分析求解，可以起到事半功倍的作用，有利于提高教学效果.

［1］沈传墉.替代、等效及密勒定理的进一步探讨[J].电工教学，1996，18(3):78-83.

［2］卢容德.关于替代定理的内涵与外延[J].电子电气教学学报，2000，22(4):115-117.

［3］邱关源，罗先觉.电路[M].5版.北京:高等教育出版社，2006.

［4］Matthew N O Sadik，Sarhan MMusa,Charles K Alexander.Applied Circuit Analysis[M].New Your:Mcgraw Hill Education，2012.

［5］Thomas L Floyd，David M Abchla.DC/AC Fundamentals:A Systems Approach[M].Kom ton:Pearson Schweiz Ag，2012.

［6］刘惠，白凤仙，董维杰，等.电路课程中替代定理教学的探讨[J].电子电子教学学报，2010，32(3):27-29.

［7］张柏顺，刘泉.再谈替代定理[J].电气电子教学学报，2003，25(3):101-103.

［8］张美玉，杨扬，齐家国，等.含受控源电路替代定理的研究[J].浙江工业大学学报，2001，29(2):171-175.

［9］周蕾.替代定理在含受控源电路中的应用[J].电气电子教学学报，2011，33(4):49-51.

［10］卢容德.叠加定理在非线性电阻电路中的应用[J].长江大学学报，2006，3(2):42-45.

Research and Application of Substitution Theorem

DAI Guang-zhen，WANG Guan-ling
（College of Electrical Engineering，Anhui Polytechnic University，Wuhu 241000，Anhui，China）

The Substitution Theorem is based on the voltage and current of a two terminal circuit in a known circuit, which simplifies the circuit analysis by means of equivalent substitution and facilitates the optimization of the circuit design.In the existing circuit analysis textbook,there is controversy for the lack of description.Therefore,the Substitution Theorem is re-described,given its various forms and proof,and explains the disputes.Finally,through examples of flexible use of Substitution Theorem for circuit analysis,it can play a multiplier role,which is beneficial to the actual circuit analysis and circuit theory teaching.

substitution theorem;equivalent;circuit

TM131；TM133%

A%%%

1007-5348（2017）03-0043-04

（责任编辑：邵晓军）

2016-11-08

安徽省教育厅重大教研项目（2015zdjy082）；安徽工程大学校级教学团队（2016jxtd03）.

代广珍（1974-），男，安徽无为人，安徽工程大学电气工程学院副教授，博士；研究方向：新型存储器及材料.