三维泥沙动力数值模型的高效应用——准三维模型“轻装”效应

杨 静，黑鹏飞，假冬冬，尚毅梓

(1.中央民族大学 生命与环境科学学院， 北京 100081；2.南京水利科学研究院 水文水资源与水利工程科学国家重点实验室， 江苏 南京 210029;3.中国水科院 流域水循环模拟与调控国家重点实验室, 北京 100038)

三维泥沙动力数值模型的高效应用
——准三维模型“轻装”效应

杨 静1，黑鹏飞1，假冬冬2，尚毅梓3

(1.中央民族大学 生命与环境科学学院， 北京 100081；2.南京水利科学研究院 水文水资源与水利工程科学国家重点实验室， 江苏 南京 210029;3.中国水科院 流域水循环模拟与调控国家重点实验室, 北京 100038)

近年来泥沙动力和河床冲淤三维计算模型(SB3D)取得了快速的发展，然而由于SB3D基于全三维水动力模型，计算量过大将会降低SB3D的工程实用性。从模型结构、模型求解与程序代码编译三个角度，探讨准三维水动力模型和SB3D联用的合理性和实用性，并采用实验室模拟和工程应用予以证明。结果表明：准三维模型多数条件下可以为SB3D提供合理的三维水流速度；全三维水动力模型和程序模块可以方便的由准三维模型和模块替换；准三维水动力模型极大的提高了模型计算效率，具有理想的“轻装”效应，可以提高SB3D的工程实用性。

准三维模型；计算河流动力学；泥沙

河流动力模型包含水动力模型和泥沙动力模型。近年来复杂形态河道演变数值模拟研究，促进了三维泥沙动力模型(SB3D)的迅速发展[1-7]。但是，这些模型都基于全三维水动力模型[3-6]，而当前计算机速度尚无法满足全三维模型工程计算的要求，限制了SB3D最新成果在工程中的应用。准三维水动力模型基于静压假定，极大的提高了三维模型的计算效率，增加了三维水动力模型的应用可行性[2]。当前准三维模型越来越多的应用于河流水库的水质模拟中[8-9]，遗憾的是，基于准三维水动力模型的泥沙动力模型研究仍相对较少，准三维河流动力模型的应用优势尚未展现。工程应用中，当全三维模型因计算量过大而不具有可行性时，则直接选取二维[10-13]或一维泥沙动力模型[14-15]，而未将SB3D模块应用于准三维模型，由此导致准三维河流动力模型应用的滞后性。

本文在对全三维和准三维水动力模型进行理论分析和试验对比(时均流速)的基础上，将全三维模型的SB3D应用于准三维模型，探索其在准三维河流动力学模型中的应用可行性和优越性。

1 准三维水动力模型分析

1.1 准三维水动力模型

河流全三维水动力模型求解主要难点源于自由表面和压强项。在水位起伏不大的条件下，常由连续方程直接垂向积分获得水位方程。自由表面获得后，压强并无独立的控制方程，对此需要采用经典流体力学求解方法，常用方法为SIMPLE法。每一次压强修正迭代，都需要求解一个七对角方程。若采用GMRES方法求解，Im、Jm、Km分别表示x、y、z方向的网格数，则计算量为O(Im×Jm×Km)3，如每一时间步中压力修正n步，则总计算量为O(n×(Im×Jm×Km)3)。

静压假定后，动量方程中压强p可由水位ζ简单表示。ζ与动量方程常采用分离求解，先采用显式求解ζn+1，再分别由动量方程和连续性方程先后求得x、z、y方向流速un+1、vn+1和wn+1，无需采用全三维模型常用的压力修正法迭代求解[2]。其中最为简单的是水位和动量方程全部显式求解(如POM模型)。或者仅对垂向扩散项隐式离散(如EFDC模型)，所得三对角方程也无需迭代求解，追赶法求解计算量仅为O(8Km×Im×Jm)。

水位方程

(1)

水平动量方程

(2)

(3)

垂向流速由下式

(4)

(5)

直接显式离散求得。以上各式中t为时间，x、y、z为物理坐标；σ=(z-zb)/H，zb为床面高程，H为水深；u、v分别为x、y方向的流速；ω、w分别为σ坐标下和z坐标下的垂向流速；f、g分别为科氏力和重力加速度；Fx和Fy分别是x和y方向的动量源项。

总之，虽然准三维模型并不适用于垂向速度(w)变化较大情况，但准三维和全三维水动力模型都可以为SB3D提供三维流速信息，且准三维模型基于静压假定，降低了水动力模型求解难度，增加三维模型的求解效率。目前关于准三维水动力模型开放型代码较多，其中相对成熟且应用较多的是EFDC。本文水动力学语言模块(HYD)由Intel Visual Fortran 11.0.061专业版编译器双精度Fortran90语言编写。

1.2 准三维水动力精度分析

河道形态如图1所示，弯道的底坡为0.0003。试验流量为4.17 L/s、下游水深10.59 cm[16]。模型进口紊动动能k=0.02U2(U为垂向平均流速)，紊动黏性系数为νt=0.001 m2/s；模型横向网格数10个，纵向网格数360个，垂向网格数10个。

理论分析已表明，由于垂向动量方程直接采用静压假定，因此准三维模型无法准确计算垂向流速(w)，不适合于垂向流速变化较大的情况，也就是说准三维模型无法准确计算涉及垂向流速的二次流。本文分别采用三维水动力和准三维水动力方程，对图1弯道水动力进行计算，验证弯道中水流流速大小沿垂向的变化，结果表明，准三维模型和三维模型流速大小相差甚小。图2给出第三弯道45°和75°断面流速沿垂向分布对比。由图2可看出全三维、准三维模型数值计算值与实测值基本符合。只是数值计算流速在近床面明显降低，沿垂向呈对数分布，而实测流速在近床面略有波动，甚至出现近底层流速相对较大的现象，这可能由于弯道位置断面螺旋流所致。模型验证表明，虽然基于静压假定，但在动压作用非主导条件下，准三维模型流速计算结果与全三维模型基本一致。准三维水动力模型可以为SB3D提供可靠的水流流速信息。

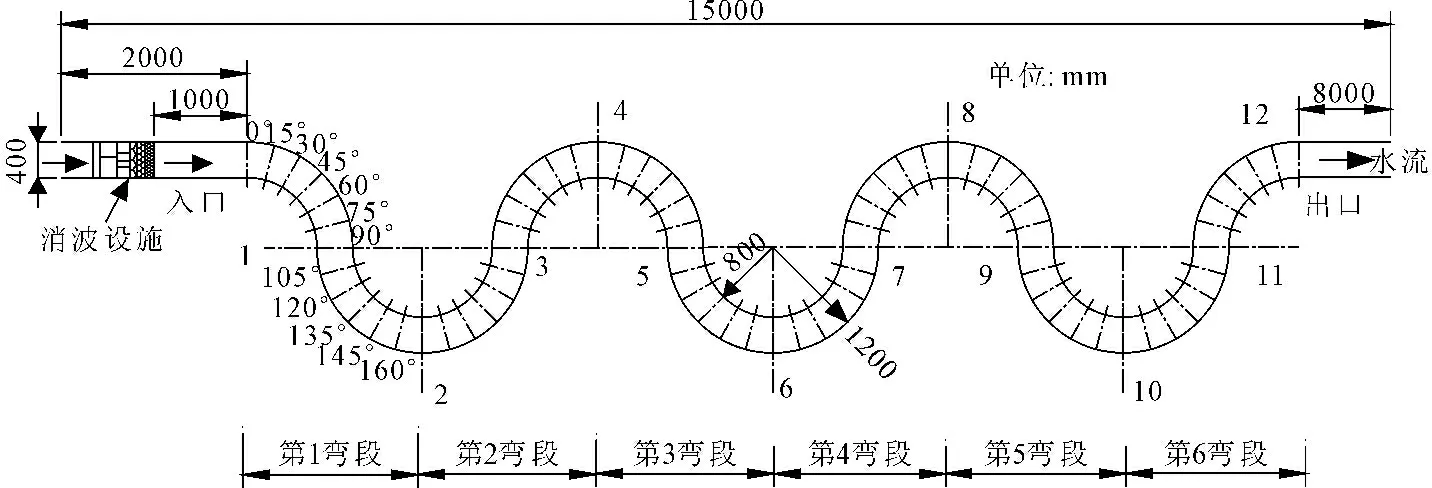
图1 连续弯道模型平面布置图

图2 典型断面流速沿水深分布验证

2 三维泥沙动力模型及高效应用

目前三维水动力模型和泥沙动力模型都采用分离求解。在每一时间步内，先求解水动力学方程获得un+1、vn+1和ωn+1，后求解泥沙输运方程和河床变形方程获得泥沙浓度(sn+1)、水位高程(zn+1)等(见图3)。un+1、vn+1和ωn+1得出后，泥沙动力模块自身封闭。若该泥沙动力模型的un+1、vn+1和ωn+1由准三维水动力模型提供，则称为准三维河流动力学模型(见图3)。

(1) 悬沙输运模型。无论是全三维模型还是准三维模型，悬沙输运方程均采用单相多组分流体输运方程[2-6]，只是在垂向对流项中增加了泥沙垂向沉速ωs：

(6)

式中，ωs为σ坐标下的泥沙沉速；Qs为泥沙源项。

图3 全三维河流动力学模型和准三维河流动力学模型的转换

由于单相多组分控制方程应用的广泛性，多数准三维模型程序语言都包含相关模块，只需要在程序代码中添加垂向沉速，并修改床面边界条件以及相应参数即可用于悬沙计算。床面边界可采用

(7)

式中，νt是紊动扩散系数；σs为泥沙的Schmidt数；sb和sb*分别为近底层泥沙浓度和饱和浓度。

(2) 河床变形模型。河床纵向变形模型的一般形式

(8)

式中

(9)

其中角标l表示粒级级配分组；lM为泥沙级配组数；p′为泥沙的空隙比；δb为推移质泥沙运动层的厚度；qb,l,x和qb,l,y分别在x和y方向泥沙推移通量。

不同文献中上式各项具体形式不同，但具体计算都是采用显式求解，因此全三维模型研究成果，都可直接用于准三维模型，且程序代码的实现也可统一。此外，河床横向演变模型也都采用显式求解[1,3-6]，因此同样可直接应用于准三维模型。

3 模型工程应用

3.1 工程概况

北本水电站位于湄公河上游河段，为湄公河水电开发规划的第一级电站，电站位于老挝北部乌多姆赛省北本县境内，坝址在北本县城上游约14 km处。电站采用径流式开发，枢纽工程由混凝土重力坝、泄洪冲沙闸、冲沙底孔、船闸和鱼道等建筑物组成(见图4)。水库为日调节水库，水库正常蓄水位340 m，死水位334 m，总库容约7.8×108m3，电站装机容量912 MW。

图4 电站及下游航道分布平面示意图

根据规划，当入库流量小于3 a一遇洪水流量13 200 m3/s时，水库水位尽量维持在340 m运行，通过泄洪冲沙闸(12孔)、冲沙底孔来维持；当入库流量大于3 a一遇洪水流量13 200 m3/s、小于5 a一遇洪水流量14 900 m3/s时，船闸停止使用，水库水位尽量维持在340 m运行，通过泄洪冲沙闸(12孔)、冲沙底孔和机组过流、航道冲沙闸打开泄水(2孔)来调节。电站推移质泥沙大都被上游电站拦截，悬沙中值粒径为0.007 7 mm，电站下游床沙中值粒径0.025 mm。

3.2 离散网格和边界条件

计算区域上游选自大坝位置，出口取至引航道以下500 m位置。模型采用了曲线正交网格，纵向网格数为129个，横向网格数为60个，垂向分为5层。网格划分主要考虑主流流向以及水流、泥沙参数的变化。网格与引航道边界拟合很好，主流区网格走向与河道深泓线一致，网格间距为10 m～20 m，引航道区域网格局部加密。区域网格夹角为80°～90°。时间步长为10 s。计算区域上游边界给定水库下泄流量和沙量，下游给定水位(见图5)。

图5 下游出口水位变化过程曲线

基于所建立准三维模型，计算2003年—2009年水库修建之前的河道冲淤过程，参数率定表明，模型饱和系数采用常数，冲刷时取2.3，淤积时取0.55，床面粗糙高度ks=0.01 m。

3.3 引航道表层横向流速和通航安全分析

北本水电站通航建筑物为单线单级船闸，船闸级别为Ⅳ级，要求口门区垂直航线的横向流速不能大于0.30 m/s，回流区不能大于0.40 m/s。本文选取通航最低流量、年平均流量、2 a一遇流量以及通航最大流量四种条件计算引航道的横向流速。计算结果可以清楚的反映表层和底层的流速差异(见图6)，表层流速可为航道通航安全提供有力依据。引航道回流区位于航道内口门上游100 m～300 m处，如图7中C#区。航道内横向流速随着河道下泄流量增加而增大。在最低通航流量和年平均流量时，C#区横向流速为0.10 m/s左右，对船只的安全航行无不利影响，回流流速小于0.40 m/s，尚能满足通航要求，但已有碍航趋势；当流量达到2 a一遇流量11 600 m/s时，航道内C#区最大横向流速达0.50 m/s～0.60 m/s，超过口门区最大横向流速限值0.40 m/s，无法满足通航条件。上述计算结果表明，相较于二维模型，准三维模型可以方便的提供引航道内表层流速，进一步判断不同水流条件下船只航行的安全性。

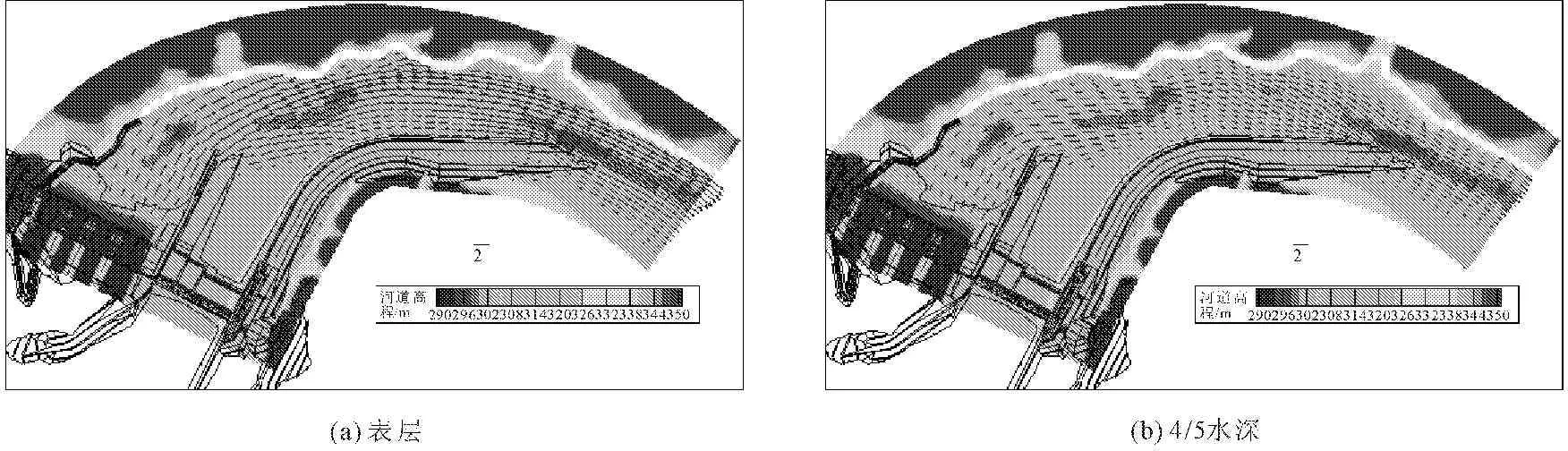
图6 计算全域三维流场分布

3.4 电站下游泥沙冲淤计算

模型基于Dell/戴尔T420服务器(六核E5-2430V2/16G/2T)，对电站运行后下游泥沙冲淤进行计算。电站下游主河道及引航道冲淤示意图如图8所示。计算表明，电站运行后下游河道沿深泓线均有不同程度的冲刷，断面冲刷由深泓线向两岸递减。最大冲深位于坝下游300 m处深槽位置，水库运行1 a后，最大冲深达1.0 m左右，后冲刷的速度逐渐减缓，运行1 a～5 a内，该点年平均冲刷深度0.5 m，至第5年时冲淤基本平衡，河道深泓线平均冲刷1.4 m～2.0 m左右，局部达3.0 m。当河道泄洪冲沙闸关闭时，泄洪冲沙闸下游形成局部回流和淤积，淤积厚度约为0.7 m。在电站运行10 a内，下引航道呈累积性淤积趋势。淤积程度由口门向船闸呈递减趋势，5 a末船闸附近淤积厚度约为1.0 m左右，口门最大淤积厚度达2.6 m左右，将会出现碍航现象。以上计算表明，准三维模型不仅可以区分垂向速度差异，而且可以成功模拟电站下游河道长期冲淤过程，对比全三维模型在计算效率方面具有更大的优势。计算机运行时间约为214 h，模型适用于中小型的工程的应用。

图7 引航道流速分布

图8 电站下游主河道及引航道冲淤示意图

4 结 论

近年来泥沙输运和河床冲淤计算方法取得了较快的发展，但这些模型的水动力计算多是采用全三维水动力模型，计算量过大而限制了成果的工程实用性。本文研究表明：

(1) 准三维水动力模型可以极大的降低模型的计算量，同时较为准确的模拟非动水压强主导的三维水流运动特征。

(2) 全三维河流动力模型中的水动力模型和模块，可方便的被准三维模型或模块取代，变为准三维模型，增加其工程应用可行性。

(3) 准三维水动力模型可以成功应用于中长尺度河流模拟，特别是对于部分既需要考虑三维垂向流速分布，计算时空尺度又较大的泥沙动力模拟。

[1] Olsen N R B, Kjellesvig H M. Three-dimensional numerical flow modeling for estimation of maximum local scour depth[J]. Journal of Hydraulic Research, 1998,36(4):579-590.

[2] 黑鹏飞,假冬冬,冶运涛,等.计算河流动力学理论体系框架探讨[J].水科学进展,2016,27(1):152-164.

[3] 黄国鲜,周建军,吴伟华.弯曲河道螺旋流作用下的物质输运三维模拟[J].清华大学学报(自然科学版),2008，48(6):977-982.

[4] 假冬冬,邵学军,王 虹,等.考虑河岸变形的三维水沙数值模拟研究[J].水科学进展,2009,20(3):311-317．

[5] 假冬冬,黑鹏飞,邵学军,等.分层岸滩侧蚀坍塌过程及其水动力响应模拟[J].水科学进展,2014,25(1):83-89.

[6] 胡德超,钟德钰,张红武,等.三维悬沙模型及河岸边界追踪方法:Ⅱ—河岸边界追踪[J].水力发电学报,2010,29(6):106-113.

[7] Motta D, Abad J D, Langendoen E J, et al. A simplified 2-D model for meander migration with physically-based bank evolution[J]. Geomorphology, 2012,163/164:10-25.

[8] Tang C Y, Li Y P, Acharya K. Modeling the effects of external nutrient reductions on algal bloomsin hyper-eutrophic Lake Taihu, China[J]. Ecological Engineering, 2016，94:164-173.

[9] Chen L B, Yang Z F, Liu H F. Assessing the eutrophication risk of the Danjiangkou Reservoir based on the EFDC model. Ecol. Eng.[EB/OL]. http://dx.doi.org/10.1016/j.ecoleng.2016.02.021.

[10] 方红卫,王光谦.平面二维全沙泥沙输移数学模型及其应用[J].应用基础与工程科学学报,2000,8(2):165-178.

[11] 夏军强,宗全利,许全喜,等.下荆江二元结构河岸土体特性及崩岸机理[J].水科学进展,2013,24(6):810-820.

[12] 周 刚,王 虹,邵学军,等.河型转化机理及其数值模拟—Ⅰ模型建立[J].水科学进展,2010,21(2):145-152.

[13] 钟德钰,张红武.考虑环流横向输沙及河岸变形的平面二维扩展数学模型[J].水利学报,2004,35(7):14-20.

[14] 李义天,尚全民.一维不恒定流泥沙数学模型研究[J].泥沙研究,1998(1):81-87.

[15] 方红卫,王光谦.一维全沙泥沙输移数学模型及其应用[J].应用基础与工程科学学报,2000,8(2):154-164.

[16] Wang B, Jia D D, Zhou G, et al. An experimental investigation on flow structure in channel with consecutive bends[C]//Proceedings of 16th IAHR-APD Congress and 3rd Symposium of IAH R-ISHS. Berlin: Springer, 2009:1811-1816.

3D River Fluvial Numerical Model Optimized by the Quisi-3D Hydrodynamic Numeric Model

YANG Jing1, HEI Pengfei1, JIA Dongdong2, SHANG Yizi3

(1.CollegeofLifeandEnvironmentalSciences,MinzuUniversityofChina,Beijing100081,China;2.StateKeyLaboratoryofHydrology-WaterResourcesandHydraulicEngineering,NanjingHydraulicResearchInstitute,Nanjing,Jiangsu210029,China;3.DepartmentofWaterResources,ChinaInstituteofWaterResourcesandHydropowerResearch,Beijing100038,China)

Quasi-3D numerical model has been widely used in the water flow modeling and water quality modeling, but its significance in the river fluvial computation has not be fully realized. In this paper, the quasi-3D hydrodynamics model and fluvial model used in the 3D model were combined. After the model calibration, the model were then used to simulate the hydrodynamic and fluvial process in downstream of the Beiben power station. Results manifested that quasi-3D numerical model for the river dynamics shows great advantage than the 3D numerical model in the computation efficiency while retaining the capability for simulating the vertical distribution of the flow and sediment dynamics. The quasi-3D numerical model plays the irreplaceable role when the vertical distribution of the flow and sediment are needed while 3D was not feasible due to the computation efficiency.

quasi-3D numerical model, compuational river dynamics; sediment

10.3969/j.issn.1672-1144.2017.02.002

2016-12-11

2017-02-01

中央民族大学校级自主科研项目(2016SHXY03)；国家自然科学基金项目(51209239)

杨 静(1982—)，女，内蒙古赤峰人，博士生，研究方向为水生态。E-mail:yangjing123456@126.com

黑鹏飞(1979—)，男，陕西榆林人，讲师，主要从事地表水环境和水生态研究。E-mail:heipf06@mails.tsinghua.edu.cn

TV143

A

1672—1144(2017)02—0009—07