一种水下高速运动目标的双阵纯方位TMA方法

吴旭

摘要：水下高速运动目标运动分析有其特殊性，其一即为本舰不允许进行机动，故单阵纯方位目标运动分析不适于分析水下高速运动目标，本文基于双阵方位测量值分析其运动状态。纯方位目标运动分析是典型的非线性估计问题，文中利用扩展卡尔曼滤波算法进行双阵纯方位目标运动分析，从而解算出目标运动要素。文章通过数值仿真分析算法性能，验证了该方法的有效性。

关键词：目标运动分析；纯方位；扩展卡尔曼滤波

中图分类号：TN911 文献标识码：A 文章编号：1007-9416（2017）03-0234-01

TMA的基本问题即是利用带噪的阵元域数据估计出目标的运动要素[1]。在现代战争实际环境中，测得的目标特征数据通常极其有限，而目标的方位几乎成了唯一可靠的参数，因此BO-TMA具有十分重要的意义[2-4]。

水下运动目标的运动要素估计有其特殊性，其一是本舰不允许机动，其二是TMA算法的快速收敛性，因此单阵BO-TMA并不适用，文中采用双阵方位测量值进行TMA，基于扩展卡尔曼滤波算法（EKF）处理该非线性系统，通过计算机仿真分析了不同条件下算法性能，仿真结果表明：与单阵BO-TMA相比，该算法无需本舰机动即可实现对水下目标的运动分析。

1 双阵纯方位TMA原理

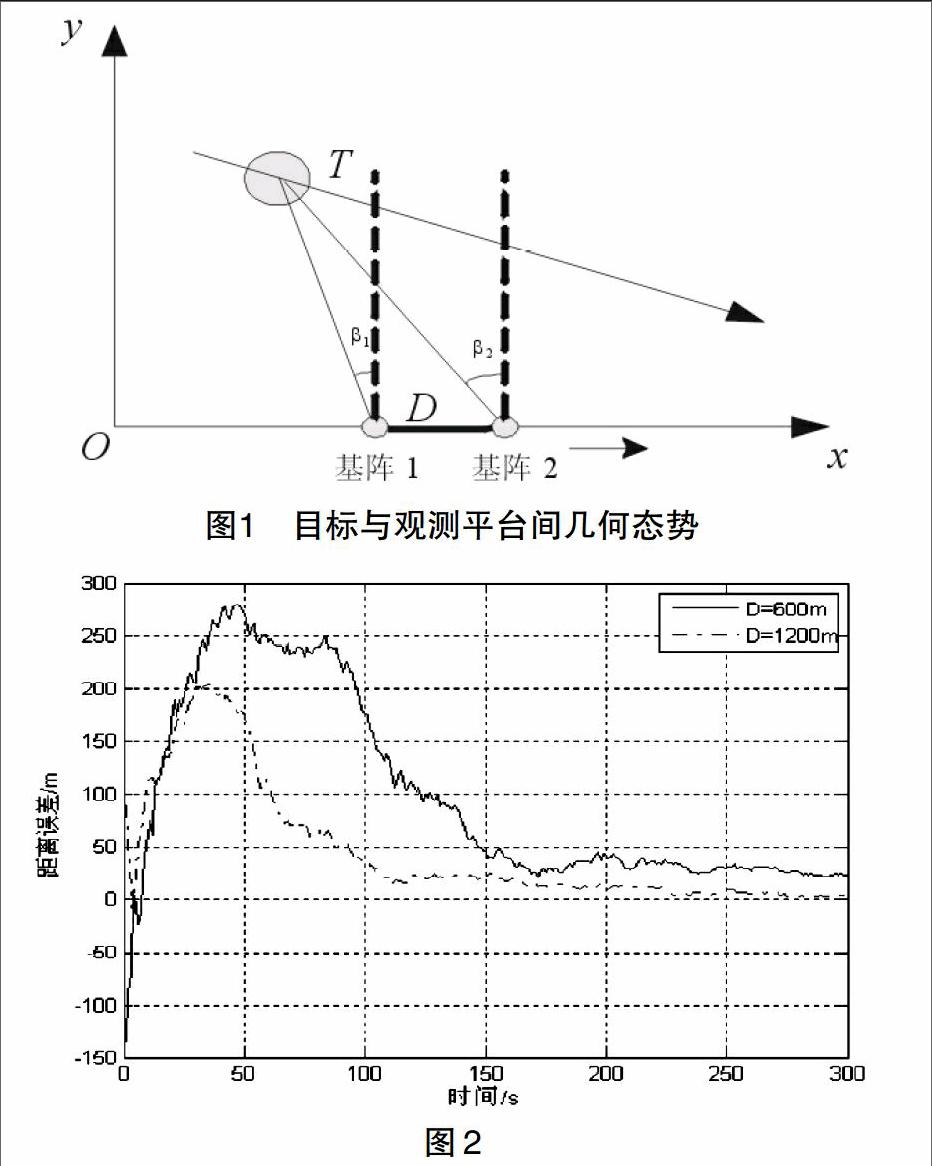
考慮如图1所示的基阵与目标间的几何关系，假定二维平面情形，两基阵均随本舰匀速直线运动，阵间距离D可预先测量并能实时修正，目标于平面内匀速直线运动。

表示目标的绝对运动状态（即相对坐标原点的运动状态，下同），其中分别为目标相对坐标原点的方向与方向的距离，分别为目标相对坐标原点的方向与方向的速度； 表示阵1的绝对运动状态，表示阵2的绝对运动状态。

表示目标相对于基阵1的运动状态，其中分别为目标相对基阵1的方向与方向的距离，分别为目标相对基阵1的方向与方向的速度，表示目标相对于基阵2的运动状态，其中分别为目标相对基阵2的方向与方向的距离，分别为目标相对基阵2的方向与方向的速度。、如上图所示，分别为基阵1、基阵2所测得的目标方位角。以基阵1为参考基阵，则有状态方程如下：

（1）

式中：为状态转移矩阵，为过程噪声，其自相关矩阵为Q，G为过程噪声转换矩阵。

简记为，测量方程如下：

（2）

其中：为量测噪声，其自相关矩阵为R，且有：

（3）

由式（3）可知，系统为非线性，经典的EKF算法非常适合处理此类问题[5]。对于非线性系统，EKF算法基于泰勒展开对其线性近似，然后利用卡尔曼滤波算法完成对目标状态的估计。

2 仿真计算

基于上述方法进行仿真计算。仿真条件：双阵间距D分别为600m和1200m；双阵方位测量误差均为正态随机变量，标准差分别为1.5°和0.5°，方位测量间隔T为1秒；本舰绝对航速6m/s，航向正东，基阵1的初始位置为（-D，0），目标初始位置为（-6000m，6000m），目标绝对航速20m/s，绝对航向120°。

图2给出了不同D情形下算法仿真结果。其中，方位测量误差标准差取0.5°。由图可知，D越大，收敛速度越快，估计性能愈好。

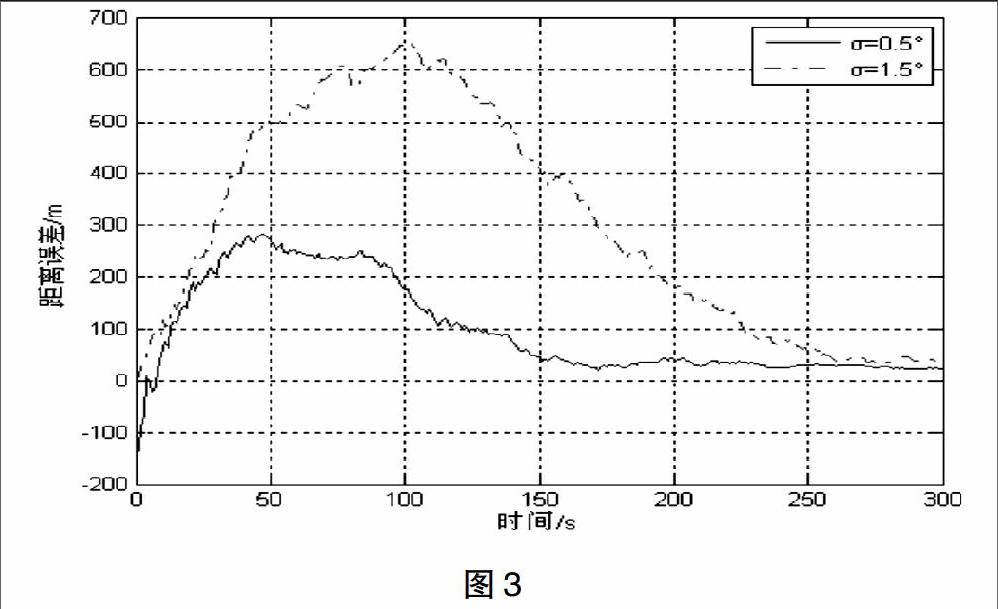
图3给出了不同方位测量误差下仿真结果。其中，D取600m；方位测量误差均值取0。由图可知，方位测量误差方差越小，收敛速度越快，估计性能越好。

仿真结果表明：基于EKF算法能实现双阵纯方位目标运动分析，且无需本舰执行机动。双阵间距、观测噪声影响算法性能，间距越大，噪声越小，算法性能越好。

3 结语

本文将EKF算法拓展到双阵TMA领域中，文章通过计算机仿真分析不同条件下算法性能，仿真结果表明算法的可行性，且双阵间距越大、观测噪声越小，算法性能越好。该算法是实时处理方法，不需存储大批量数据，非常适合工程实现。

参考文献

[1]O. Tremois， J. P. Le Cadre. Target Motion Analysis with multiple arrays： Performance Analysis[J].IEEE Transactions on Aerospace and Electronic Systems.1996， 32（3）：1030-1046.

[2]Yun Jun Zhang， Guo Zhong Xu. Bearings-Only Target Motion Analysis via Instrumental Variable Estimation[J].IEEE Transactions On Signal Processing. 2010， 58（11）：5523-5533.

[3]Claude Jauffret， Denis Pillon. Bearings-only maneuvering target motion analysis from a nonmaneuvering platform[J].IEEE Transactions on Aerospace and Electronic Systems， 2010， 46（4）：1934-1949.

[4]Laleh Badriasl，Kutluy l Dogancay. Three-dimensional Target Motion Analysis using azimuth/elevation angles[J].IEEE Transactions on Aerospace and Electronic Systems， 2014， 50（4）：3178-3194.

[5]Bruce. P. Gibbs.Advanced Kalman filtering， least-squares and modeling： a practical handbook[M].New Jersey： John Wiley & Sons，2009.