双臂对称性对关联成像算法的抗误差能力分析

陶忠良++赵文卓

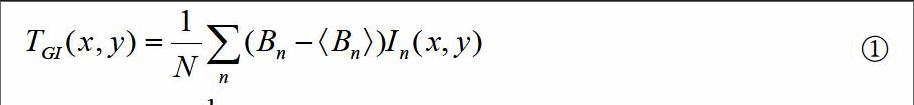
摘要：为了分析在实际成像过程中双臂误差对不同关联成像算法的影响。理论上推导了双臂横向误差和轴向误差对传统关联成像算法（ GI），差分关联成像（DGI）和基于压缩感知的关联成像算法（CSGI）的影响，并对其进行了比较。

关键词：图像重构；峰值信噪比；关联成像；双臂误差

中图分类号：TP391 文献标识码：A 文章编号：1007-9416（2017）03-0167-01

关联成像在传统的成像算法中起着重要作用，通常我们称其为“鬼”成像（GI），在很多领域均有应用。关联成像的组成主要分为两部分，一是激光照射到物体的时候不经过物体而是直接接收光場空间分布信息的参考臂，二是接收到总光强的物臂。

我们选取100*100的二值图像“Stripes”和灰度图像“Lena”为研究的重构目标，从理论研究上对双臂的轴向以及横向的正负误差它们对GI、DGI、CSGI三种算法的影响。在研究过程中我们的衡量指标是（PSNR）峰值信噪比，通过轴向和横向误差的不同取值实施实验仿真，将GI，DGI和CSGI三种算法取同样的测量次数，对比了不同轴向与横向误差重构图像的PSNR。

1 GI，DGI和CSGI成像原理与目标重构方法研究

通常情况下的关联成像系统是从激光器发射出激光投射在旋转毛玻璃形成散斑场组成了赝热光源，之后通过50/50的分束棱镜将其分成了两束同样的光。在这个过程中形成了物臂，是指当中的一个光束经过调制之后经过探测器（无空间分辨率桶）能够接收到总光强信号。而另一束光直接通过具有空间分辨率的CCD接收它没有通过物体，为这个时候记载的光场空间信息。

下面公式是GI算法的重构公式

①

公式中，当双臂间存在横向误差的时候，倘若CCD检测到的光场与实验的探测平面相错a行b列，为记物臂端物体面的散斑场，这时，可以通过公式①重构点（m， n）时

②

公式②里表示的自相关函数表示的是散斑场的中点（m+a， n+b），而公式中的代表的是点（m+a， n+b）和其他点之间的互相关函数值。因为每个点的散斑场的强度是随机波动，相关功能明显点（m+a， n+b）和附近的点作用在函数上的值远大于他点的值，公式②中的是一个常数而已，通常的散斑场的平均强度分布的空间高度随机光场是均匀的，即任意一点的平均强度近似相等，这对重构影响不是很大。公式②重构得到的传输函数实为。由于散斑相干深度在轴向方向，所以在点相关函数（m，n）的值仍很大，但随着δZ的增加点（m，n）值必须降低，当δz 超出相干光场的轴向深度以外，将无法重建，也就是说随着δZ的增大，GI重构物体的图像将越来越模糊，最终无法实现重构。

DGI算法与GI算法相比，DGI算法在参考臂端既记载光场总光强信息又检测光场的空间分布信息，而且最后重构了物体的交流信息，背景噪声得到了很大程度的降低，DGI的重构效果要好于GI的重构效果，DGI的重构公式是

③

和GI同样，重建的对象其实点（m+a， n+b）交流传输系数、横向位移，采用常用的图像重建算法重建图像的平移图像，重构图像错位较大，峰值信噪比会下降。如果轴向误差δZ存在于双臂间时，DGI和GI影响相似，那就是，随着δZ的增加，即物体的图像重建会越来越模糊，最终无法实现重建。

CSGI算法将压缩感知理论运用到研究中，能够达到测量次数少但是重构出物体像的信噪比高，CSGI算法将压缩感知理论运用到研究中，可对高信噪比的对象的形象，而且提高了算法的计算复杂度。CSGI变换测量每个CCD为行向量，散斑场矩阵和最后的测量矩阵是由N幅散斑场构成测量矩阵G。但是对于CSGI算法来说，只要有误差存在于双臂间，其重构结果必将受较大影响，重构图像的PSNR会随着误差的增大而迅速下降。

2 结语

该文对GI，DGI，CSGI算法从理论上论述分析了在传统关联成像系统中，横向误差或轴向误差存在于双臂间的影响。论述结果表明，当双臂间因为不对称的存在横向或轴向误差时，GI、DGI、CSGI的抗误差效果是，GI最佳，DGI次之，CSGI最差。

参考文献

[1]刘雪峰，姚旭日，李明飞，俞文凯，陈希浩，孙志斌，吴令安，翟光杰.强度涨落在热光鬼成像中的作用[J].物理学报，2013，62（18）： 184205-184205.

[2]仲亚军，刘娇，梁文强，赵生妹.针对多散斑图的差分压缩鬼成像方案研究[J].物理学报，2015，64（1）：14202-014202.

[3]王森，李洪国，张德建，赵秋丽，王海波，熊俊，汪凯戈.毛玻璃转速对热光鬼成像质量的影响[J].量子光学学报，2015（1）：9-13.