基于四色原理技术的伪四色算法研究

郭林庚

摘要：利用开放的电子地图手工绘制的非规范性地图信息，本文旨在针对这些错综复杂的不规范地理信息，提出一种伪四色原理算法，自动分析多边形相邻性，使用尽可能少的颜色进行地图着色，开发者无须了解地理信息系统原理，即可快速掌握，快速开发，节约公司成本。

关键词：数据可视化；四色原理；最小外接矩形；空间位置分析

中图分类号：P208 文献标识码：A 文章编号：1007-9416（2017）03-0159-02

1 前言

电信经营数据可视化系统使用百度地图，手工绘制各管辖区域，地图手工着色变得不可行。四色原理[1]，“任何一张地图只用四种颜色就能使具有共同边界的国家着上不同的颜色。”将四色算法应用到系统中，进行自动着色，能解决手工无法着色的问题，提升系统展示感知。但不规范的多边形覆盖物空间位置相邻性分析是四色算法应用的难点。本文阐述了一些简单易懂图形基本处理算法和过程，面对错综复杂的非规范性地图信息，提出着色的伪四色算法，使得没有地理信息相关专业知识的内部开发人员能快速掌握，迅速开发，减少开发投资成本。

2 空间位置相邻性分析

2.1 射线法判断多边形覆盖物相邻（算法1）

分析实际绘图情况，一线人员绘制的多边形都出现相交的情况，因此可采用判断多边形上的每个点是否有在另一个多边形内，来判断两多边形是否相邻。几何上判断某个点是否在多边形内，可以采用射线法[2]进行计算。射线法原理：从目标点出发引一条射线，看这条射线和多边形的多有边的交点数目，如果有奇数个交点，则说明在内部，如果有偶数个交点，则说明在外部。本算法内容涉及到地理信息信息的基础算法及图形学的内容，非本文介绍的重点，只做算法比较参考。

2.2 最小外接矩形算法（算法2）

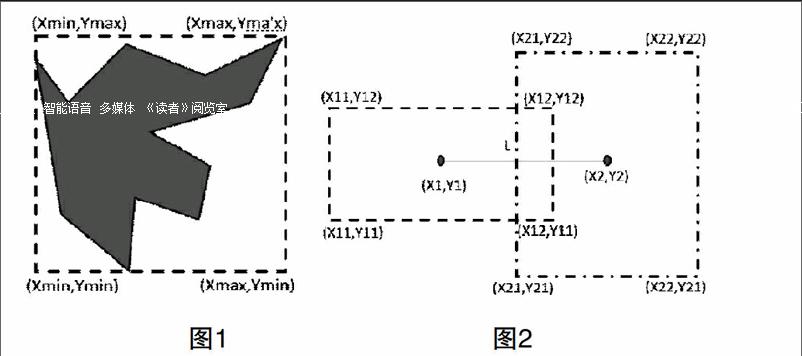
计算坐标集的最大维度，最小纬度，最大经度，最小经度，形成一个多边形的最小外接矩形，如图（1）。当两个矩形的中心距离小于等于矩形1与矩形2的宽的和的一半时，两个矩形相交或相邻，如图（2）所示，即

以此判定绘制的多边形相邻。此算法根据地理要素的大致位置来判断区域相邻，则会扩大了实际区域的相邻关系数。

2.3 多边形最小相邻距离算法（算法3）

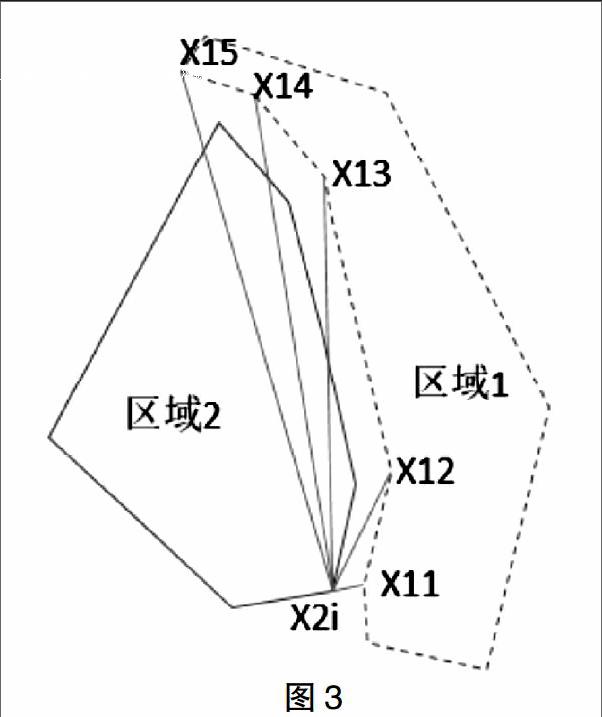
分析实际绘图情况，相邻区域多边形无法做到边界重叠，但绘制边界趋势基本相当，如图（3）。因此计算两个多边形俩俩坐标点间的距离，并取最小值。如果小于特定值，则可判断两多边形区域相邻。

2.4 算法应用结果对比

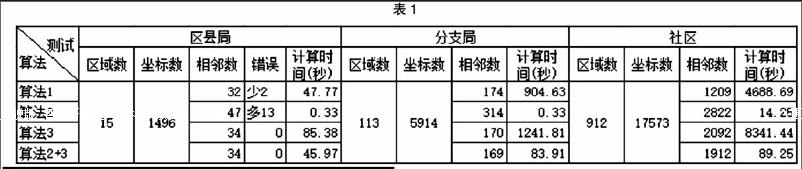
经过一线人员手工绘制，管辖区域分成三个层级，一级15个区县局，二级113个分支局，三级912个社区。测试环境Oracle10g数据库。特定值的选取，一级比例尺500m-1km，选择100m；二级比例尺100m-200m，选择50m；三级社区20m-50m，选择20m。如表1所示。

2.5 算法优化

如上表所示，最小外接矩形的算法2速度最快，但是它误差大。最小相邻距离的算法3，速度最慢，但是准确率高，在一级层面准确率100%。算法1，出现相交的时候，准确度尚可，但无相交则判断错误，且运行速度慢。可采用混合算法，即先进行算法2大致相邻区域判断，然后在判断的结果中对有相邻关系区域再进行算法3的判断，既提高了算法准确率，又提高了算法的计算速度。实际应用结果显示，在区县局层面正确率100%，三级社区层面执行时间在90秒内。

3 伪四色原理算法设计

3.1 无递归的伪四色算法

定义可变长的颜色组T，计算1到i-1个区域中，且与第i区域相邻的区域的不同颜色组C，从T中剔除C中的颜色，并取最小颜色值赋给第i个区域赋，如果找不到颜色，则增加颜色组T的颜色，流程图如图（4）所示。

3.2 带递归的四色算法

定义固定长度数组T，T的颜色值最大为待着色区域群众的最大俩俩相邻数。算1到i-1个区域中，且与第i区域相邻的区域的不同颜色组C，从T中剔除C中的颜色，并取最小颜色值赋给第i个区域；如果找不到颜色，则回退到第i-1区域，并修改第i-1区域的颜色，重新开始着色，流程图如图（5）所示。

3.3 实际着色结果验证（表2）

4 结语

通过实际着色测试结果可以看出，无论是使用那种算法，都能实现自动着色。最后数据可视化系统选择效率最高且颜色数最少的混合算法配合递归着色。规范绘图，提高绘图质量，调整错误的相邻区域，使得最大俩俩相邻数不超过4，则本文算法也可以实现四色地图着色。

参考文獻

[l]徐志才.四色问题的探讨[J].北京邮电大学学报，2003，（2）：105-112.

[2]张宏，温永宁，刘爱利.地理信息系统算法基础[M].北京科学出版社，2006.