基于直觉模糊集的灰色模型故障预测①
2017-05-17王开军林品乐福建师范大学数学与计算机科学学院福州350007福建师范大学福建省网络安全与密码技术重点实验室福州350007
王开军, 林品乐(福建师范大学 数学与计算机科学学院, 福州 350007) (福建师范大学 福建省网络安全与密码技术重点实验室, 福州 350007)
基于直觉模糊集的灰色模型故障预测①
王开军, 林品乐
(福建师范大学 数学与计算机科学学院, 福州 350007) (福建师范大学 福建省网络安全与密码技术重点实验室, 福州 350007)
复杂设备的故障特征具有不确定性, 非线性等特点. 针对故障预测具有不确定性, 将模糊数学中的直觉模糊集和灰色模型相结合设计故障预测的方法. 新方法利用隶属度函数设计了描述系统运行正常的正常直觉模糊子集和运行异常的异常直觉模糊子集, 利用灰色模型计算系统运行的预测值, 并计算预测值的正常隶属度; 再分别计算预测值的正常隶属度与正常直觉模糊子集和异常直觉模糊子集的贴近程度来实现故障预报. 该方法通过三容水箱系统T2水箱水位变化预测三容水箱系统是否出现故障和通过UH-60行星齿轮盘裂纹何时开始增大的故障进行实验. 实验验证了该方法的可行性, 可及时准确地预测出系统故障.
隶属度; 贴近度; 直觉模糊子集; 灰色模型; 故障预测
1 引言
随着工业技术的发展, 现代工业系统的规模越来越大、结构越来越复杂, 带来更高的经济利益和生产效率的同时, 也使得影响系统正常运行的因素增多,引发故障的潜在因素变多. 检测设备和系统何时出现故障对生产和人身安全是非常重要的. 设备和系统何时出现故障的迹象具有不确定性和模糊性, 并且故障预测本身也是具有不确定性和模糊性的. 基于灰色理论的灰色模型和直觉模糊集适合于描述和分析不确定性和模糊性的问题. 由于直觉模糊集同时考虑了隶属度和非隶属度两方面的信息, 因此在处理信息的能力比模糊集要强, 对不确定性的描述有更强的实用性[1];灰色系统理论着重研究概率统计、模糊数学等所难以解决的“小样本”、“贫信息”不确定性问题[2].
灰色方法已经在故障预测中应用, 例如: 文献[3]利用PSO算法改进灰色模型的参数优化, 有很高的预测精度; 文献[4]针对样本数据量较小条件下的故障预测问题, 提出了一种灰色相关向量机故障预测模型;文献[5]结合粗糙集和灰色理论的各自特点, 提出一种用于变压器故障预测的新方法; 文献[6]对当前故障预测方法单独考虑各特征参数的缺陷, 将灰色多变量预测模型—MGM(1, n)模型引入机械故障预报. 上述文献中有灰色模型单独应用于故障预测中的, 也有与别的方法相结合的故障预测. 直觉模糊集有应用于决策等问题[7,8], 但是还未有应用到故障预测上, 并且还未有灰色模型与直觉模糊集相结合应用于故障预测方面研究的文献.
本文结合灰色模型和直觉模糊集来进行故障预测,对文献[9]和文献[10]中预测数据只考虑其隶属度而未考虑非隶属的情况进行改进, 且提高了算法的运行效率.
2 灰色模型和直觉模糊相关方法简介
2.1 灰色GM(1,1)模型
定义1[11]. 设X(0)=(x(0)(1),x(0)(2),…,x(0)(n) )为非负序列, X(1)为X(0)的1-AGO(一次累加)序列, X(1)=(x(1)(1),x(1)(2),…,x(1)(n )), 其中
x(k), 则称:

为GM(1,1)模型的原始形式. 称:
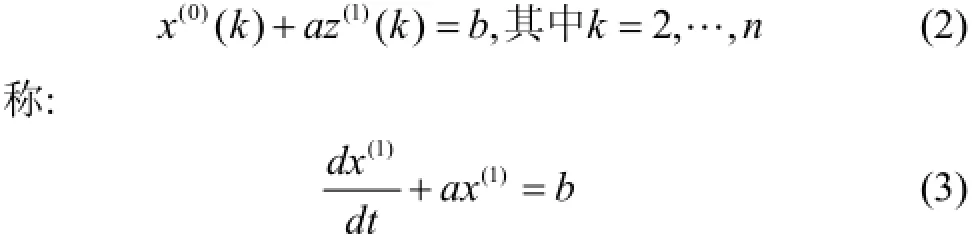
为式(2)的白化方程, 也称影子方程.
对参数a和b的估计, 主要通过式(2), 采用最小二乘法估计, 得出:

定理1[11]. 设B, Y和aˆ如定义1所述,=(BTB)-1BTY , 则:①白化方程=b的解, 也称时间响应函数, 为:
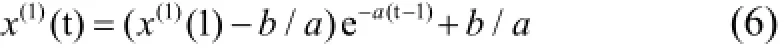
② GM(1,1)模型x(0)(k)+az(1)(k)=b的时间响应序为:

2.2 模糊隶属度及直觉模糊集
本文用到模糊数学中的隶属度及隶属度函数这一经典概念, 其定义参见文献[12].
定义2[13]. 设X是一个给定的非空论域, 则X上的一个集合A形如: A={<x,μA(x),γA(x) >}, 的三重组称为A是X上的一个直觉模糊集(IFS), 其中函数: μA:X →[0,1]和γA:X→[0,1], 且满足0≤μA(x)+γA(x)≤1(∀x∈X), 称μA(x)和γA(x)分别为X上x属于A的隶属度和非隶属度.
从上述定义可以得知模糊子集相对应的直觉模糊子集为: A={<x,μA(x),1-μA(x)>|x∈X }.
对论域X上的直觉模糊集A, 称πA(x)=1-μA(x)-γA(x)为A中x的直觉指数(Intuitionistic Index), 描述了x对A的犹豫程度(Hesitancy degree), πA(x)≤1, ∀x∈X. 因此直觉模糊集也可以表示成: A=(μA,γA,πA)/x. 可以看出, 模糊子集为直觉模糊子集的一个特例, 即当πA(x)=1-μA(x)-(1-μA(x ))=0时.
3 使用直觉模糊集的灰度模型故障预测
依据故障征兆进行的故障预测具有不确定性, 判断其发生故障与否也具有模糊性. 灰色模型可以通过少量的、不完全的信息, 建立灰色微分预测模型, 对事物发展规律作出模糊性的长期描述[14]. 模糊数学中扩展的直觉模糊子集可以表示事物判断的模糊性. 因此,这里把灰色模型和模糊数学中直觉模糊子集相结合进行故障预测方法的设计.
先设计正常、异常隶属度函数, 并用正常、异常隶属度函数获得正常模糊子集和异常模糊子集, 再根据灰色模型估计系统运行的预测值{~yt}, 计算这些预测值{~yt}属于正常(运行情况)的隶属度{Dt}再分别计算{Dt}与正常直觉模糊子集和异常直觉模糊子集的贴近度, 当{Dt}与异常直觉模糊子集的贴近度大于与正常直觉模糊子集的贴近度时, 预报可能出现故障.
3.1 算法设计
假设观测数据的前k个时刻的数据服从高斯分布,则设计观测值落在距离该高斯分布的均值3个标准差之内属于正常数据, 即属于正常的隶属度函数值为0.5以上(分母中的常数10来控制3个标准差之内隶属度函数值为0.5以上); 当观测值在3个标准差之外设置为异常数据, 属于异常的隶属度值为0.5以下(分母中的常数10来控制3个标准差之内隶属度函数值为0.5以下).
依据上述思路, 设计正常隶属度和异常隶属度分别如下.
定义3. 正常隶属度函数:
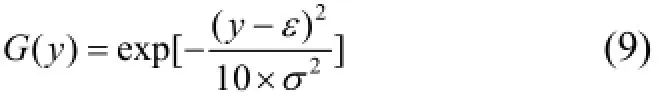
G(y)中的ε和σ分别为初始连续k个时刻的正常数据的均值和标准差; y为观测数据和预测数据.
定义4. 异常隶属度函数:

G′(y)中的ε和σ分别为初始连续k个时刻的正常数据的均值和标准差时; y为观测数据和预测数据. 当数据整体是递增的时, 公式中指数的分子为数据与均值加6倍标准差的差值的平方; 相反当数据整体是递减的时, 公式中指数的分子为数据与均值减6倍标准差的差值的平方.
定义5. 直觉模糊集的海明贴近度公式如下[13]:
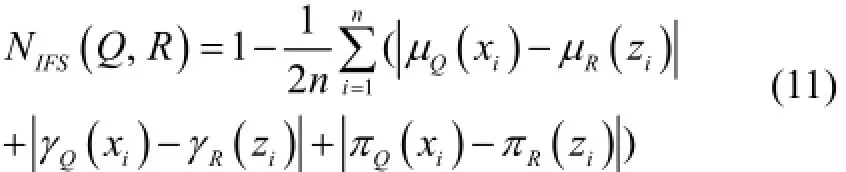
其中μQ(xi)与μR(zi)分别为直觉模糊集Q和R中的第i个隶属度. γQ(xi)与γR(zi)分别为相对应于直觉模糊集Q和R的第i个非隶属度. πQ(xi)和πR(zi)为直觉模糊集Q和R在第i个的直觉指数, 在本文中πQ(xi)和πR(zi)都设为0. 式中NIFS(Q, R)越大, 说明直觉模糊集Q和直觉模糊集R越相似; 反之, Q和R越不相似.
3.2 故障预测算法步骤
Step1. 设设备正常运行时的初始m个时间点的观测数据为{yt}(t=1,2,3,…,m), 计算该观测数据的均值和标准差, 供公式(9)、(10)使用.
Step2. 利用公式(9)和公式(10)计算前k(k<=m)个连续正常运行的观测数据G0的正常隶属度和异常隶属度, 获得正常直觉模糊集合Ak(即元素个数为k的正常直觉模糊子集)和异常直觉模糊集合Bk(即元素个数为k的异常直觉模糊子集).
Step3. 在当前时刻t, 利用灰色模型计算出预测值{y~i}(i=t+1, t+2, …, t+k), 并利用公式(9), 计算连续的k个预测序列数据的正常直觉模糊集合Dt.
Step4. 利用公式(11)分别计算Dt与正常直觉模糊子集Ak和异常直觉模糊子集Bk的贴近度.
Step5. 在时刻点t, 若Dt与Bk的贴近度(异常贴近度)大于Dt与Ak的贴近度(正常贴近度)时, 预报故障即将来临.
4 实验结果与分析
在故障发生后多长时间预报故障作为本文方法性能和有效性的评价指标. 本文方法分别与基于改进余弦相似度的粒子滤波故障预报[15]、基于随机摄动粒子滤波器的故障预报算法[16]和基于粒子滤波的FDI方法[17]进行对比, 并与文献[9]和文献[10]的算法运行效率进行对比.
实验一仿真实验采用文献[17]中德国Amira 公司制造的三容水箱系统, 如图1所示. 有关该水箱系统的更多细节参见文献[16]. 若出现故障. 圆筒T2的液位h2 将不能保持初始值而大幅下降[15].
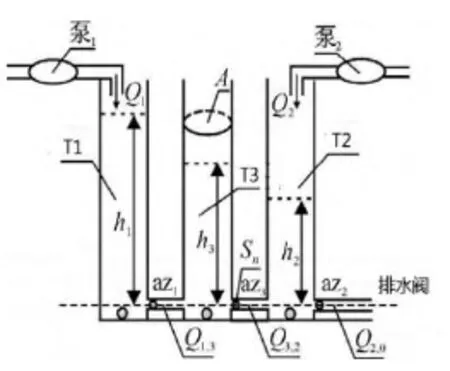
图1 三容水箱系统
在该实验中, 按T2水位初始0.3下降10%为发生故障故[16], 据此可推知其标准差为σ=(m-(0.3-0.3*10%))/4, (考虑观测值出现在m±3σ之外还有0.3%的概率, 把标准差扩大到±4σ)m为观测数据时刻1到时刻20的均值. 其中灰色模型是以每10个观测数据为一组进行预测, 贴近度是使用公式(11)计算的, 其中γQ(xi)和γR(zi)分别为正、异常直觉模糊子集的非隶属度, 即为1减正、异常隶属度, 在此基础上考虑了非隶属度情况进行实验.
根据本文算法步骤得到实验结果见图2(取k=6时的预报结果, k的取值参考文献[10]), 表1列出了对应图2的具体贴近度数据, 其贴近度是子集元素个数为6进行计算的, 因此表中所显示的时刻是6的倍数.

表1 本文方法对三容水箱(T2)的故障预报时的贴近度

表2 文献[10]方法的三容水箱(T2)故障预报及贴近度

表3 文献[16]方法的三容水箱(水箱T2)预报结果

图2 本文方法对三容水箱(T2)的预报结果
对比算法--基于模糊贴近度的粒子滤波故障预测方法[10]的故障预报及贴近度见表2. 从本文方法的表1(用了非隶属度的直觉模糊集情况)和对比方法结果的表2(未用非隶属度的模糊集情况)中可以看出, 本文方法考虑了非隶属度的贴近度计算, 增加了对非隶属度的权重, 从而得到的预报结果比基于模糊贴近度的粒子滤波故障预测提前了6个时间点.
本文方法的三容水箱(T2)实验结果为k=6时在时刻54处预报故障(见图2), 比对比的基于改进余弦相似度的粒子滤波故障预报[15](见图3)提前了9个时间点,比基于随机摄动粒子滤波器的故障预报算法[16](见表3)提前了10个时间点.
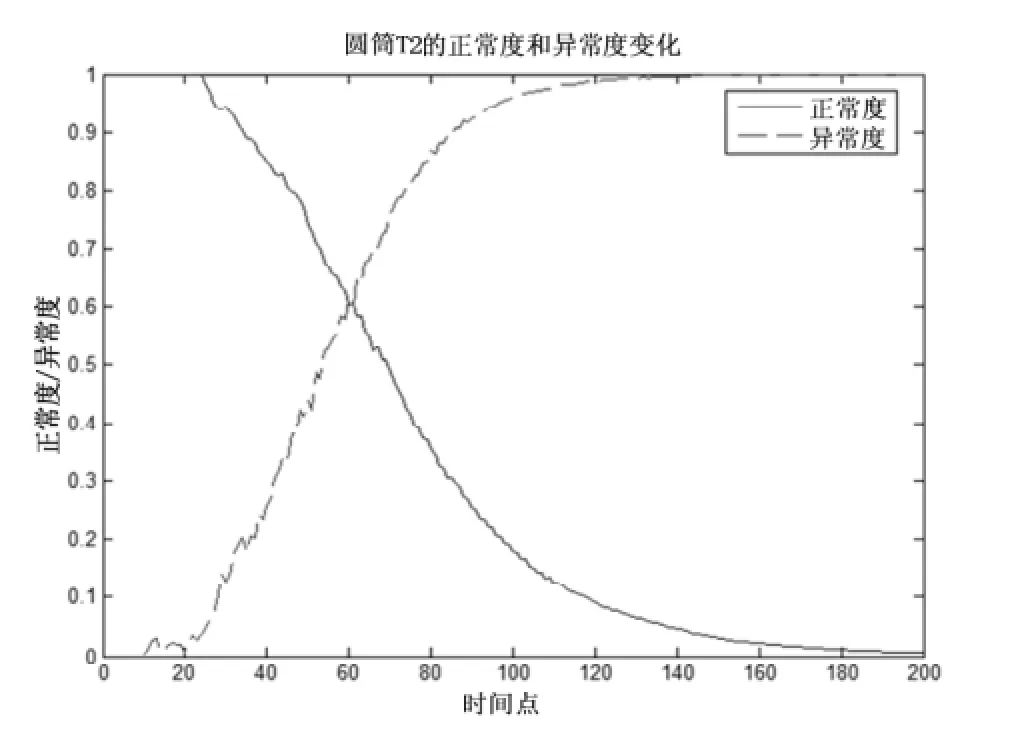
图3 文献[15]方法对三容水箱(水箱T2)的预报结果
本文方法与基于基于模糊隶属度的粒子滤波故障预测[9]和基于模糊贴近度的粒子滤波故障预测[10]在三容水箱(水箱T2)实验中算法运行效率对比如表4. 从表4中可以看出, 本文的算法在三容水箱实验中的运行速度比文献[9]和文献[10]算法快很多.

表4 三容水箱(T2)实验中各算法运行时间
实验二是对UH-60行星齿轮盘裂纹何时开始增大的故障[17]进行预报. 其中灰色模型是以每10个观测数据为一组进行预测. 贴近度是使用公式(11)计算的, 其中γQ(xi)和γR(zi)分别为正、异常直觉模糊子集的非隶属度, 即为1减正、异常隶属度, 在此基础上考虑了非隶属度情况进行实验.
根据本文算法步骤得到实验结果见图4(取k=9时的预报结果, k的取值参考文献[10])和表5(对应图4的具体贴近度数据). 其贴近度是子集元素个数为9进行计算的, 因此表中所显示的时刻是9倍数.

图4 本文方法对UH-60的预报结果
对比算法基于模糊贴近度的粒子滤波故障预测[10]的故障预报及贴近度见表6. 从本文方法的表5(用了非隶属的直觉模糊子集情况)和对比方法的表6(未用非隶属度的模糊集情况)中可以看出, 本文方法和对比的文献[10]方法在相同的时刻点预报故障, 能够合理的描述系统的运行状态.
本文方法的UH-60实验结果为k=9时在时刻126预报出故障(见图4), 比基于改进余弦相似度的粒子滤波故障预报[15](见图5)提早了4个时间点, 比基于粒子滤波的FDI方法[17](见图6)提早了9个时间点预报出故障.
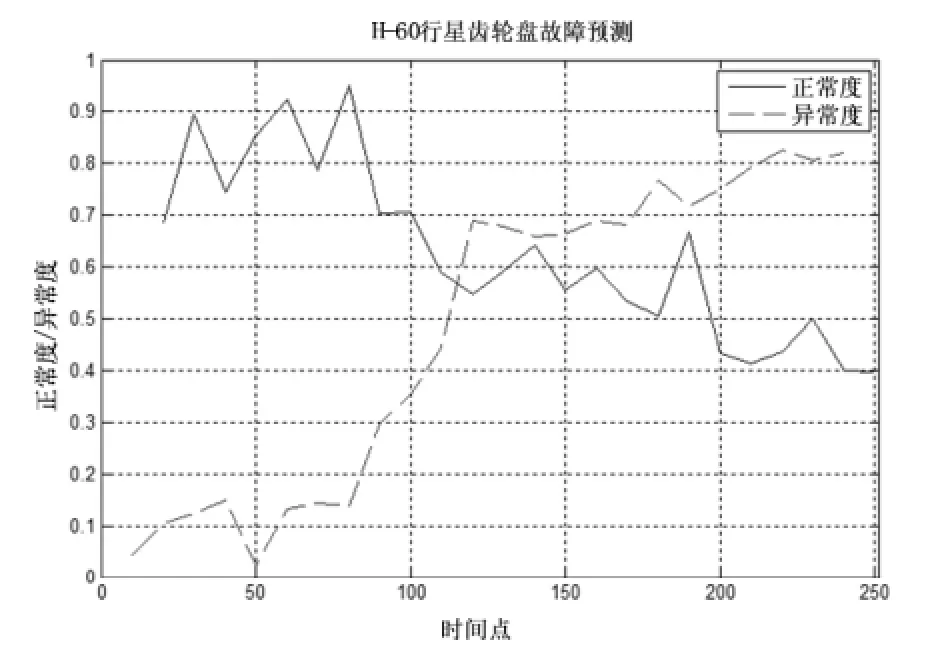
图5 文献[15]方法对UH-60的预报结果
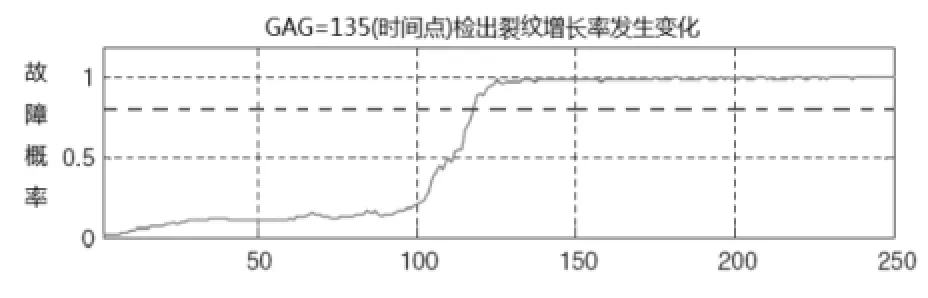
图6 文献[17]方法对UH-60的预测结果

表5 本文方法对UH-60故障预报时的贴近度

表6 文献[10]方法对UH-60的故障预报及贴近度
本文方法与基于模糊隶属度的粒子滤波故障预测[9]和基于模糊贴近度的粒子滤波故障预测[10]在UH-60实验中算法运行效率对比如下(见表7). 从表7中可以看出, 本文的算法在UH-60实验中运行速度比文献[9]和文献[10]算法快很多.

表7 UH-60实验中各算法运行时间
5 总结
本文利用正常、异常隶属度函数计算得到初始正常数据的正常直觉模糊子集和异常直觉模糊子集, 再利用灰色模型估计观测值, 进一步计算预测值, 并计算预测值的正常隶属度. 将得到的正常隶属度分别与正常直觉模糊子集和异常直觉模糊子集计算贴近度,当正常隶属度与异常直觉模糊子集的贴近度大于与正常直觉模糊子集的贴近度时预报故障, 从而对设备可能出现的故障进行预报. 实验结果表明本文结合灰色模型和直觉模糊集中同时考虑隶属度和非隶属度情况的方法是可行的, 可以及时准确的预测出系统故障,与对比方法相比, 本文方法的运行速度快很多, 当系统正常/异常运行时, 本文方法预测值的隶属度与正常/异常直觉模糊子集的贴近度更接近, 显示出更好的合理性.
1 林琳.直觉模糊集在近似推理与决策中的应用[博士学位论文].大连:大连理工大学,2006.
2 崔立志.灰色预测技术及其应用研究[博士学位论文].南京:南京航空航天大学,2010.
3 李万领,孟晨,杨锁昌,等.基于改进灰色模型的故障预测研究.中国测试,2012,38(2):26–28.
4 范庚,马登武,邓力,等.基于灰色相关向量机的故障预测模型.系统工程与电子技术,2012,34(2):424–428.
5 费胜巍,孙宇.融合粗糙集与灰色理论的电力变压器故障预测.中国电机工程学报,2008,28(16):154–160.
6 杨江天,岳维亮.灰色模型在机械故障预测中的应用.机械强度,2001,23(3):277–279.
7 王毅,雷英杰,路艳丽.基于直觉模糊集的多属性模糊决策方法.系统工程与电子技术,2007,29(12):2060–2063.
8 林琳,袁学海,夏尊铨.基于直觉模糊集的多准则模糊决策问题.数学的实践与认识,2007,(5):78–82.
9 林品乐,王开军.基于模糊隶属度的粒子滤波故障预测.计算机系统应用,2016,25(6):119–124.
10 林品乐,王开军.基于模糊贴近度的粒子滤波故障预测.第六届中国数据挖掘会议(CCDM 2016).
11 刘思峰.灰色系统理论及其应用.郑州:河南大学出版社,1991.
12 Zadeh LA. Fuzzy sets. Information & Control, 1965, 8(65): 338–353.
13 Atanassov KT. Intuitionistic fuzzy sets. Fuzzy Sets & Systems, 1986, 20(1): 87–96.
14 周振民,赵红菲.灰色系统理论在节水潜力估算中的应用.中国农村水利水电,2008,(4):54–56.
15 蒋欣,王开军,陈黎飞.基于改进余弦相似度的粒子滤波故障预报.计算机系统应用,2015,24(1):98–103.
16 张琪,胡昌华,乔玉坤,等.基于随机摄动粒子滤波器的故障预报算法.控制与决策,2009,24(2):284–288.
17 Orchard ME, Vachtsevanos GJ. A particle- filtering approach for on-line fault diagnosis and failure prognosis. Trans. of the Institute of Measurement & Control, 2009, 31(3-4): 221–246.
Fault Prediction Based on Intuitionistic Fuzzy Set and Grey Model
WANG Kai-Jun, LIN Pin-Le
(College of Mathematics and Computer Science, Fujian Normal University, Fuzhou 350007, China) (Fujian Province Network Security and Cryptography Laboratory, Fujian Normal University, Fuzhou 350007, China)
The fault characteristics of complex equipment are characterized by uncertainty, nonlinearity and so on. For the uncertain fault prediction, we design a method of fault prediction,which combines intuitionistic fuzzy sets with grey model to predict fault. The new method uses the membership function to describe the normal system with the normal intuitionistic fuzzy sets and the abnormal system with the abnormal intuitionistic fuzzy sets, uses grey model to calculate predictive value, and uses membership function to calculate the membership degree. Then the fault prediction is implemented by calculating the closeness degree of predicted value of the normal membership degree with normal and abnormal intuitionistic fuzzy subset. This method predicts the fault of the three-tank-system when T2 tank starts to increase or decrease and the crack of the UH-60 planet gear plate when it starts to increase. The feasibility of the proposed method is verified by experiments, which can predict the failure of the system in time.
membership degree; closeness degree; intuitionistic fuzzy sets; grey model; fault prediction
国家自然科学基金(61572010);福建省自然科学基金(2013J01223)
2016-07-09;收到修改稿时间:2016-09-18
10.15888/j.cnki.csa.005732
