基于励磁扰动的静止自并励同步发电机参数的时域辨识
2017-05-16杨启军
张 莉,杨启军,罗 建
基于励磁扰动的静止自并励同步发电机参数的时域辨识
张 莉1,杨启军1,罗 建2
(1.重庆电力高等专科学校,重庆400039;2.重庆大学,重庆400044)
在充分考虑静止自并励发电机锯齿波励磁电压对发电机暂态过程影响的基础上,提出利用积分技术和最小二乘辨识技术,对可测量的电压、电流、功率、频率等运行参数实施发电机Park模型参数时域辨识的方法。算例仿真表明,本文所提辨识方法是可行的。
同步发电机;参数辨识;锯齿波励磁电压;积分技术;时域辨识;最小二乘
电力系统稳定性分析和电力系统仿真、故障诊断等新技术必须依靠包括同步发电机在内的电力系统模型,而同步发电机模型的准确性与发电机参数辨识的准确性有很大的关联性。
实用参数模型和派克(Park)模型[1-2]是同步发电机最常见的研究模型。在电力系统分析与计算中,普遍采用的是实用参数模型[3-6]。然而,由于实用参数模型是在忽略定子绕组暂态和转速变化对电磁转矩的影响等假设条件下得到的,所以,基于实用参数模型的发电机参数辨识平稳性较差,辨识出的实用参数不能很好地满足工程实际的需要[7]。文献[7-8]基于Park模型先辨识出各绕组的电阻和电抗等参数,然后再按照电路参数与实用参数的关系推求出实用参数,较好地改善了参数辨识的精度和有效性。但是,Park模型中各个绕组的磁链及其导数、直轴和交轴阻尼绕组的电流及其导数均为不可测量,这就需要用数值方法求解复杂的微分方程组或状态方程,导致辨识效率低下,而且会严重影响到辨识过程的稳定性和辨识结果的准确性。文献[9]在Park模型的基础上推导出由发电机定子电压、定子电流、励磁电压、励磁电流、转速等所有可测量表示的同步发电机时域模型。通过给发电机有功功率施加阶跃扰动,将发电机的扰动前后稳态数据和扰动过程中的暂态数据用于最小二乘辨识原理,分步辨识出了发电机参数。但是,该方法中最小二乘辨识的参数较多,并较多采用容易带来信号失真的微分量信号,这会严重影响辨识的准确性和稳定性,甚至得出错误的结果。不仅如此,包括文献[9-11]等在内的诸多辨识方法,普遍认为发电机稳态运行时励磁电压是恒定的直流,而现代发电厂同步发电机普遍采用静止自并励励磁方式,其稳态和暂态励磁电压实际上均是变动的锯齿波。所以,许多辨识方法在实际应用时可能会遇到困难。
针对以上不足,本文在基于Park模型方程和运动方程所建的数值模型上,设计给发电机施加一个励磁阶跃扰动(即励磁控制角阶跃扰动),并充分考虑锯齿波励磁电压对暂、稳态运行的影响。首先,根据扰动前后稳态条件下的可观测的定子绕组和励磁绕组的电流、电压及频率信号辨识出定子绕组的参数。接着,借助积分技术,利用暂、稳态可观测量巧妙地辨识出励磁绕组的参数。然后,在辨识出暂态条件下的阻尼绕组的瞬时电流积分值后,利用最小二乘原理辨识出阻尼绕组的参数。最后,通过基于Park方程、运动方程及锯齿波励磁电压数值模型自建的同步发电机暂态仿真模型进行算例仿真,验证模型和算法的有效性。
1 同步发电机Park模型
同步发电机Park模型将电机的定子绕组等效为两个与转子等速旋转的直轴绕组d和交轴绕组q,并且认为转子阻尼绕组可分解为直轴绕组D和交轴绕组Q。其电路模型包括电压方程和磁链方程,在该模型中[1],暂态过程的电压方程式(1)~(5)为磁链方程式(6)~(10)为


上述电压方程和磁链方程需要辨识的阻抗参数共有11个,包括r,rf,rD,rQ,xd,xq,xf,xD,xQ,xad,xaq。其中,各定、转子绕组的磁链及阻尼绕组电流均为不可测量,其余电压和电流可测量。
根据文献[9],将磁链方程式(6)~(10)代入电压方程式(1)~(5),消除磁链后得式(11)~(15)的暂态方程为
2 同步发电机定子绕组参数的可辨识性
根据同步发电机工作原理,在发电机稳态运行时,定子各绕组磁链ψd和ψq基本不变,其导数近似为零,故稳态时定子绕组电压方程式(1)~(2)可改写为
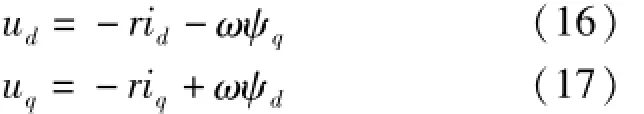
稳态运行时阻尼绕组Q,D的电流iQ和iD近似为零,故磁链方程式(6)~(7)可近似为
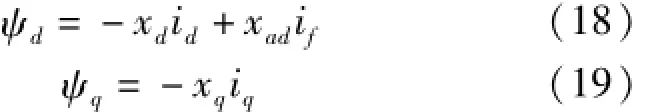
将式(18)代入式(17),式(19)代入式(16)分另可得将式(20)~(21)两端分别积分后有
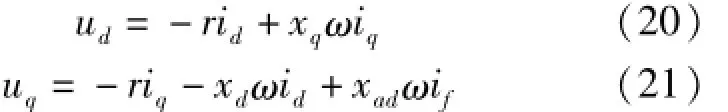

在式(22)和式(23)中,r,xd,xq,xad4个发电机参数需要辨识。根据文献[7],采用单机无穷大仿真系统,扰动前后的稳态可观测量是不一样的,故可取扰动前、后稳态各1个采样时段进行积分,建立1组线性无关的四元一次方程组,即可辨识出r,xd,xq,xad4个参数。
根据xd=xad+xσ及xq=xaq+xσ,又可得到

3 同步发电机励磁绕组参数的可辨识性
由于同步发电机稳态运行时励磁绕组磁链ψf基本为常量,其导数约为零,则励磁电压方程式(3)在某稳态时段两端积分后可近似为

由式(25)容易辨识出励磁绕组电阻如下

实际辨识rf时,为提高辨识的可信度和精度,可用扰动前后两次辨识结果的平均值作为最终值。
将磁链方程式(8)、(6)相减后求出励磁绕组磁链ψf,将其求导后代入电压方程式(3)后,容易求取定子绕组d磁链的导数为
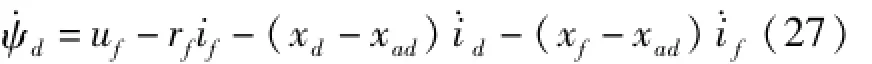
对上式进行暂态积分可得

将磁链方程式(7)代入电压方程式(2)可求得
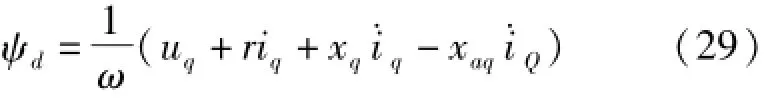
则扰动前、后d绕组稳态磁链差为
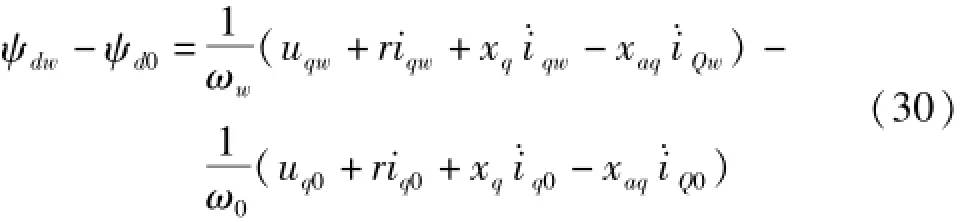
式(28)、(30)中,扰动前稳态阶段初值数据下标用“0”表示,扰动后再次进入某稳态阶段终值数据下标用“w”表示,它们之间是一个积分区间的数据。
同步发电机稳态时,阻尼绕组Q的电流iQ为零,其导数也为零;定子绕组q的电流iq为常数,其导数也为零。故式(30)可简化为
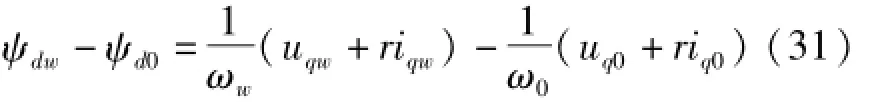
结合式(28)、(31)可求出励磁绕组电抗为
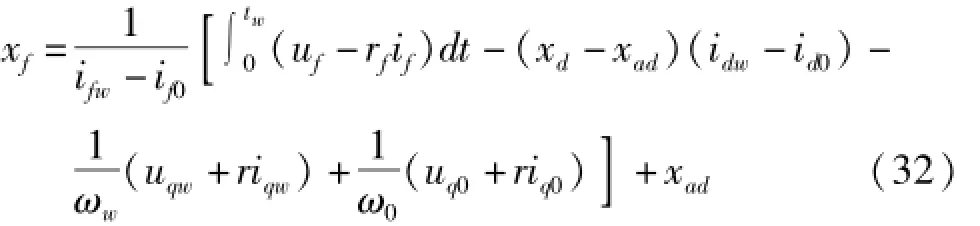
到此,根据暂态和稳态可观测量的信息,通过解析法已辨识出r,rf,xd,xq,xad,xaq和xf7个参数,且是可唯一辨识的。
4 同步发电机阻尼绕组参数的可辨识性
本文所列出的Park模型是充分考虑了发电机在励磁电压扰动条件下电磁和机械暂态的影响,参数辨识方法更具有普遍性。下面在已辨识出的r,rf,xd,xq,xad,xaq和xf7个参数的基础上对发电机阻尼绕组参数的可辨识性进行论证。
根据式(13)可得

将式(33)代入式(11)后有

将由式(34)求得的iQ代入式(12)后可求得

对式(34)、(35)两边分别积分经整理后有
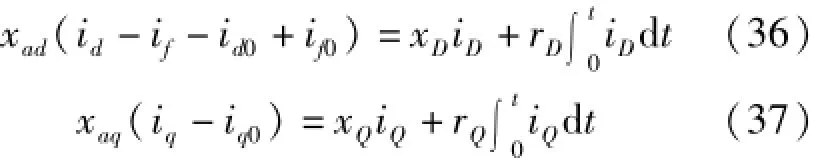
显然,式(34)、(35)两边积分后,可求出阻尼绕组若干从零时刻开始计时的不同长度时段的电流暂态积分值。然后,对式(36)、(37)分别采用最小二乘辨识技术就很容易辨识出阻尼绕组参数rD,xD,rQ和xQ。至此,所有需要辨识的11个参数已全部得到。
通过以上分析,采用本文所提出的模型,给发电机施加励磁电压阶跃扰动(即脉冲控制角阶跃扰动),充分考虑锯齿波励磁电压对暂、稳态运行的影响,用稳态和暂态过程的可测参数作为辨识的条件,就可以得到该模型的所有参数。并且,在上述可辨识性论证过程中,采用积分信号而很少使用微分信号;最小二乘辨识参数也仅为两个,且正好是需要得到的发电机参数。本文发电机参数辨识方法,不仅参数辨识的精度很高,而且满足静止自并励励磁方式发电机可测参数的特征,具有较高的可信度和实用性。
5 同步发电机阻尼绕组参数辨识方法
本文选用线性最小二乘算法辨识发电机阻尼绕组参数。最小二乘法是基于误差平方和最小的准则,来最佳拟合出符合实测数据的最优参数估计的数学方法。
根据式(36)、(37),最小二乘辨识矩阵模型为

其中:X1=[xD,rD]T
X2=[xQ,rQ]T

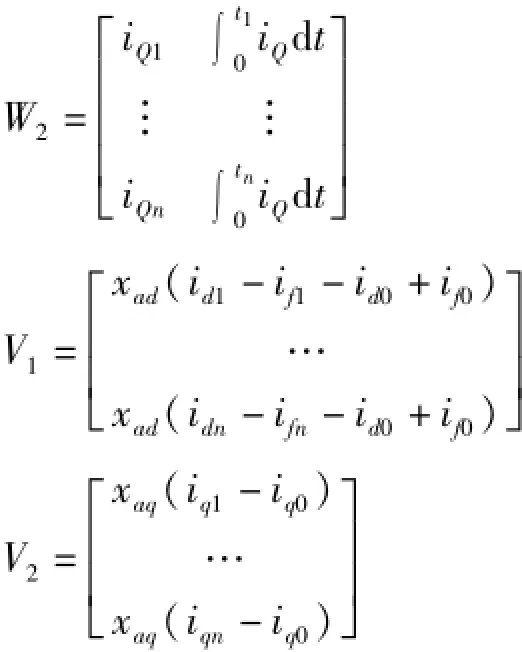
对于式(38),当n<2时,X的解由通解和特解组成,有无穷多个解;当n=2时,X有唯一解;当n>2时,可以求得Xi在最小二乘准则下的近似解。阻尼绕组参数辨识最小二乘解如下

根据文献[12],如需要,可依据辨识出的电路参数与实用参数的换算关系,得到发电机的实用参数。
6 仿真算例及分析
本文辨识用模型为SF700-56/16090大型水轮发电机,其基本参数是:SN=888.89 MVA,PN=800 MW,UN=23 kV,IN=22 313 A,fN=50 Hz,IfN=3 692 A,UN=540 V,If0=1 979 A,Uf0=273 V,nN=71.4 r/m,GD2=527 000 t·m2。励磁方式为静止自并励,励磁变额定电压为3/1.15 kV。
根据生产厂家给出的实用参数,可换算得到如下Park方程模型参数[12]:r=0.003 344,rf=0.000 444 8,rD=0.009 815,rQ=0.005 802,xd=1.040 00,xq=0.718 000,xf=0.993 803,xD=1.069 574,xQ=0.619 686,xad=0.840 000,xaq=0.518 000。其中,所有阻抗参数均为标幺值,转子基准值的选择符合xad准则,发电机励磁方式为静止自并励。
仿真系统为自并励励磁方式的单机无穷大系统。根据文献[13],水轮发电机仿真模型可采用基于Park方程模型及运动方程描述,具体可用MATLAB语言编程实现[14],但不作任何假设,以提高参数辨识的精度和可信度。根据式(40),锯齿波励磁电压可采用数值模拟方法实现,但暂不考虑换相压降。根据文献[15],励磁状态下一个锯齿波励磁电压的瞬时值表达式为

式中:uf为励磁电压;U2为励磁变压器二次侧电压;α为脉冲触发角。
具体仿真时,由原始模型仿真的波形分析可知,励磁扰动后稳定下来的实际时间约需要48 s,换算成标幺值为15 079.6;仿真步长标幺值为0.104 72时,发电机模型求解相对最稳定,对应实际仿真步长时间为0.000 333 s;扰动前发电机处于额定稳定运行状态,在t=0 s时,励磁触发脉冲控制角由1.324 7 rad(75.9°),扰动为1.371 2 rad(78.56°),获得扰动发生后暂态过程发电机出口电压和电流、励磁电压、励磁电流、转速、功率角等实测数据。
辨识D,Q绕组参数时,选择相互间隔时间为200×0.000 333 s的200组D,Q绕组电流的积分采样值进入最小二乘辨识算法。
最终,基于电磁暂态和机电暂态过程的参数辨识结果如表1所示。

表1 水轮发电机参数辨识结果
由表1可以看出,d,q,f绕组参数的辨识值与模型真值非常接近,D,Q绕组参数辨识结果稍差些,但也很理想。这证明了本文所提辨识模型和算法的合理性、有效性和准确性。
在同步发电机参数辨识方法上,本文借鉴了文献[9]模型参数辨识部分思路,但也有很大的不同。第一,参数辨识时充分考虑了锯齿波励磁电压对发电机暂、稳态的影响。第二,在充分了解各状态量仿真波形特征的基础上,采用分步辨识技术,简化了参数辨识的难度。第三,广泛采用积分原理参与参数辨识,避免大量使用容易造成参数辨识失真的微分信号,提高了参数辨识的精度和稳定性。第四,参数rD,rQ,xD和xQ辨识时,文献[11]采用最小二乘辨识方法一次辨识,最小二乘辨识系数达8个,并且rD,rQ,xD和xQ需要用这8个辨识系数换算得到。而本文用最小二乘法分两次先后直接辨识出rD和xD,rQ和xQ,辨识系数少,且参数不用换算即可得到。可见,本文所述辨识方法更为有效,辨识结果更为精确、稳定、合理。
扰动后,辨识模型仿真曲线和原始模型仿真曲线的比较如图1~8所示。特别强调:图1中励磁电压波形为锯齿波,由于巨量数据采样不便于展示锯齿波的特征,在此采用局部绘图的方法。

图1 励磁电压部分动态曲线

图2 d轴电流动态响应曲线

图3 q轴电流动态响应曲线
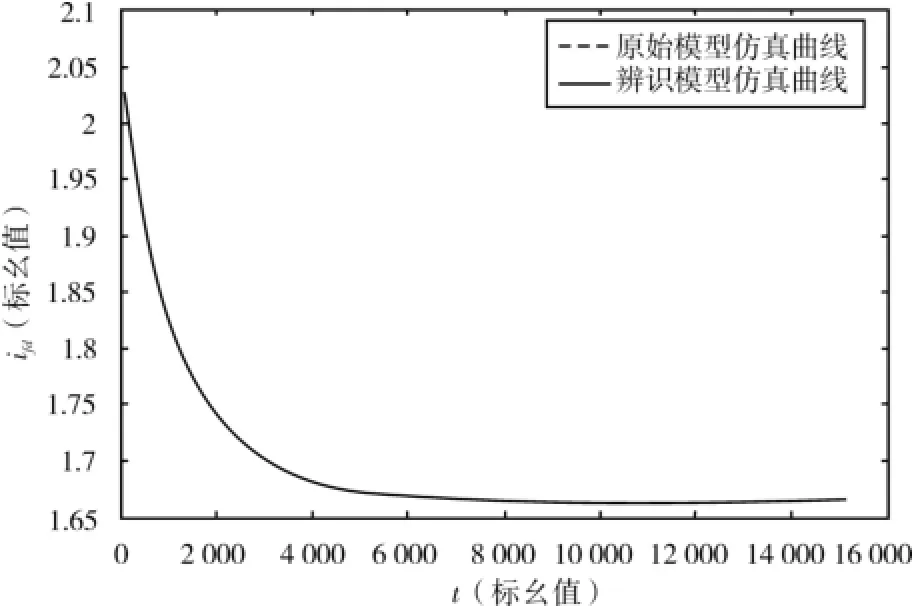
图4 励磁电流动态响应曲线
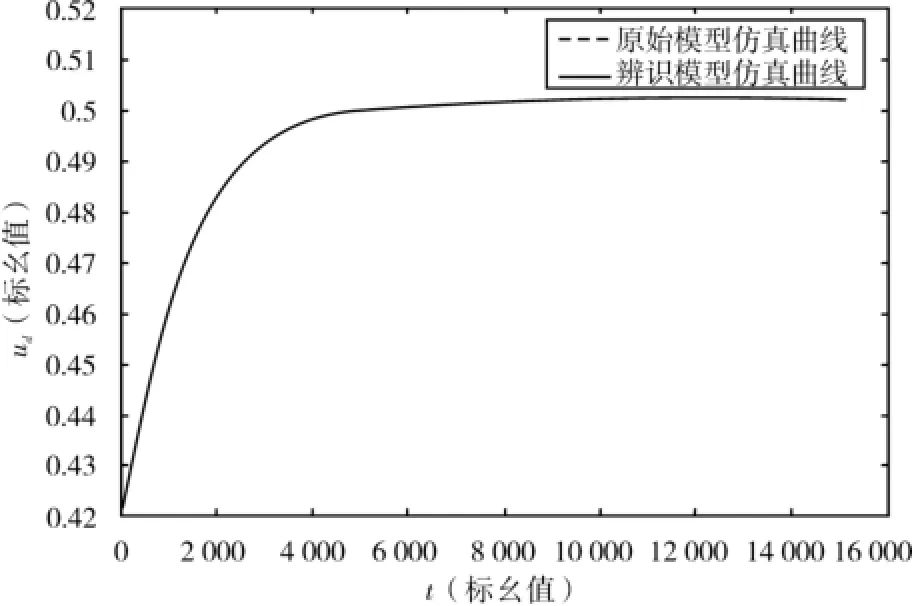
图5 d轴电压动态响应曲线

图6 q轴电压动态响应曲线
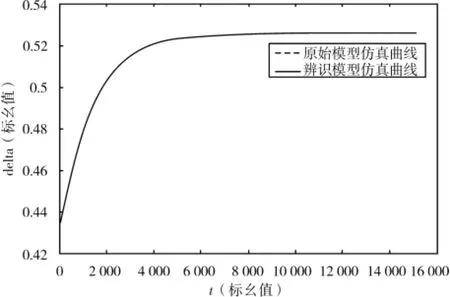
图7 功角动态响应曲线
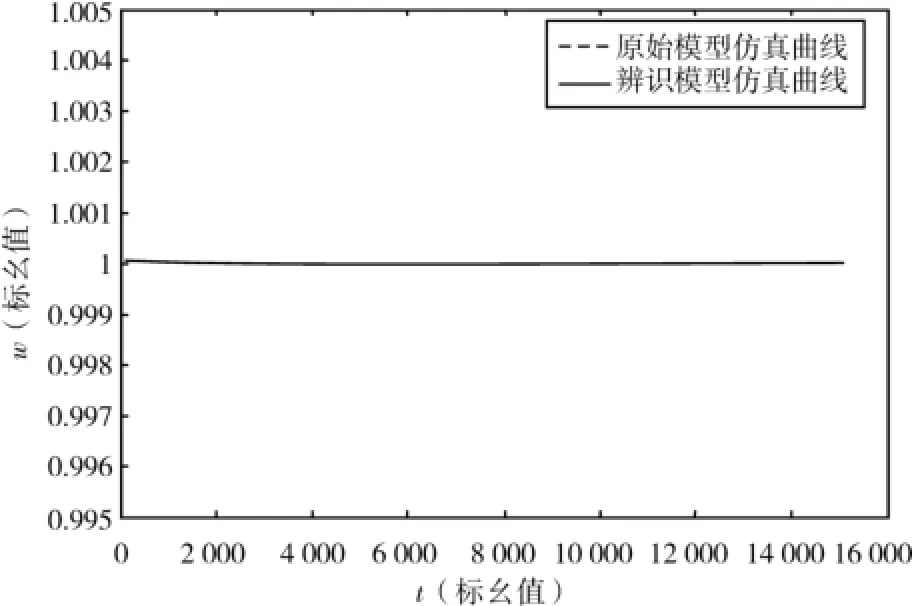
图8 转速动态响应曲线
7 结论
1)本文在Park模型的基础上导出了基于暂态和稳态过程的,由发电机转速、定子出口电压、电流、功率角以及励磁电压和电流等所有可测量量表示的同步发电机参数阶段辨识模型,降低了参数辨识的维度。
通过图1~8可以看出:0 s时励磁触发脉冲控制角由1.324 7 rad(75.9°),扰动为1.371 2 rad(78.56°)后系统进入暂态过程,48 s(对应标幺值为150 779.6)左右暂态过程结束,系统进入稳定运行阶段。在暂态和稳态过程中各原始模型仿真曲线和辨识模型仿真曲线几乎重合。这再次有力地证明了基于本文模型和算法的参数辨识是正确、可行、有效的。
2)在参数辨识过程中,为避免因采用可测量微分信号处理不当而带来的参数辨识存在较大误差和不稳定的问题,改用积分技术参与辨识过程。这种方式不仅考虑了电磁暂态过程,也考虑了机械暂态过程。阻尼绕组最小二乘辨识模型仅2个参数需要辨识,从而大大提高了参数辨识的精度和平稳性。
3)发电机模型是根据精确的Park方程和运动方程用MATLAB编程来实现的,仿真结果与根据电机学理论计算的结果非常吻合,说明发电机辨识模型可靠;锯齿波励磁电压采用数值仿真实现,辨识所需信号全部可测量,说明辨识方法满足工程实际需要;参数辨识结果误差很小及辨识模型仿真曲线和原始模型仿真曲线几乎重合,证明了基于本文所提模型参数辨识方法的合理性和有效性。
[1] 倪以信,陈寿松,张宝霖.动态电力系统的理论和分析[M].北京:清华大学出版社,2002:29-33.
[2] 昆杜拉.电力系统稳定与控制[M].北京:中国电力出版社,2001.
[3] 鞠平.电力系统非线性辨识[M].南京:河海大学出版社,1999.
[4] 金宇清,岳陈熙,甄威,等.基于功角测量的同步发电机参数辨识频域法[J].电力系统自动化,2007,31(4):7-11.
[5] JIN Y,YUE C,WEIZ,et al.On-line frequency responsemethod of synchronousmachine parameter identification based on rotor anglemeasurement[J].Automation of Electric Power Systems,2007,31(4):7-11.
[6] 陈亚民.同步发电机电磁暂态过程的实用方程[J].电力系统及其自动化学报,1995(3):7-13.
[7] 贺仁睦,郑晓雨,马进,等.基于轨迹灵敏度的负荷参数辨识范围调整方法[J].电力系统自动化,2009,33(13):17-21.
[8] RENMU H E,ZHENG X,JIN M A,et al.Amethod of parameter range adjustment in load parameter identification based on the trajectory sensitivity[J].Automation of Electric Power Systems,2009,33(13):17-21.
[9] JIANG T Z,CHEN Y X,DAN Y I.The SVD applied to the identification of the basic parameters of synchronous machine[J].Journal of Changsha University of Electric Power,2000,15(1):56-58.
[10]罗建,冯树辉,蔡明,等.基于可观测量的同步发电机参数的时域辨识[J].电力系统自动化,2011,35(7):24-27.
[11]孙黎霞,鞠平,高运华,等.基于PARK模型的同步发电机参数辨识[J].中国电机工程学报,2009,29(19):50-56.
[12]LE L X,WILSONW J.Synchronousmachine parameter identification:a time domain approach[J].Energy Conversion IEEE Transactions on,1988,3(2):241-248.
[13]沈善德.电力系统辨识[M].北京:清华大学出版社,1993.
[14]蒙泽森,何祖威,杨晨.基于时域的汽轮发电机暂态仿真[J].重庆大学学报,2006,29(8):53-56.
[15]李基成.现代同步发电机励磁系统设计及应用[M].2版.北京:中国电力出版社,2009:115-116.
A Study on the Time Domain Identification of the Parameters of the Static Self-Excited Synchronous Generator Based on the Excitation Disturbance
ZHANG Li1,YANG Qijun1,LUO Jian2
(1.Chongqing Electric Power College,Chongqing 400053,P.R.China;2.Chongqing University,Chongqing 400044,P.R.China)
Taking the influence of the exciting voltage of the STW of the static self-excited synchronous generator on the transient process of the generator into full consideration,this paper introduces the application of the parameters of Park'smodel in identifying the time domains of such measurable operating parameters as voltage,current,power and frequency by means of the integration and the LS identification techniques.The simulation examples have proved the feasibility of the identification method.
synchronous generator;parameter identification;exciting voltage of the STW;integration technique;time domain identification;LS
TM312
A
1008-8032(2017)02-0032-06
2016-12-04
张 莉(1972-),讲师,研究方向为电力系统故障分析和继电保护。
