后缘裂缝充水对裂口山滑坡稳定性的影响

杜常见，易庆林,3，张明玉，孟绘坤，文 凯

(1.三峡地区地质灾害与生态环境湖北省协同创新中心, 湖北 宜昌 443002；2.三峡大学三峡库区地质灾害教育部重点实验室，湖北 宜昌 443002；3.三峡大学湖北长江三峡滑坡国家野外科学观测研究站，湖北 宜昌 443002)

后缘裂缝充水对裂口山滑坡稳定性的影响

杜常见1,2，易庆林1,2,3，张明玉1,2，孟绘坤1,2，文 凯1,2

(1.三峡地区地质灾害与生态环境湖北省协同创新中心, 湖北 宜昌 443002；2.三峡大学三峡库区地质灾害教育部重点实验室，湖北 宜昌 443002；3.三峡大学湖北长江三峡滑坡国家野外科学观测研究站，湖北 宜昌 443002)

通过分析裂口山滑坡的GPS专业监测位移资料，初步判定其变形与降雨入渗存在一定联系，采用离散元程序3DEC 5.0模拟降雨条件下后缘裂缝充水对滑坡变形、应力状态及稳定性的影响。结果表明：裂口山滑坡后缘裂缝充水产生的滑体变形主要表现为局部变形，滑体底部水平位移明显大于顶部，且后缘裂缝内水头越高，滑体综合水平位移越大；水头H在25 m附近变化时，对滑体综合水平位移影响最为敏感。裂口山滑坡后缘裂缝内的静水压力所产生的推力不足以使该滑坡启动，后缘裂缝充水前后，底部滑面各点的有效正应力下降幅度较大，即滑面抗剪强度大幅降低，但对其稳定性影响不大。裂缝充水前后，并随着水头高度的增加，稳定系数变幅不大，滑体仍能保持稳定状态。

裂口山滑坡；后缘裂缝；充水高度；稳定性

0 前言

裂口山滑坡位于云阳县莲花乡长江干流北岸斜坡上。据史料记载，早在唐朝时代云阳裂口山就已经存在，至今几百年，地表断裂的尺寸已经达到了几十米[1]。其变形特征是山体沿61°方向开裂一裂谷，谷宽25～40 m，可见深度8～30 m，谷底为崩积物。据当地老乡反映，乾隆34年(公元1770年)时，裂口最宽处不足10 m。许多学者曾对裂口山的成因做过分析，但仍未能得到满意的结果[2]。近年来，裂口山滑坡被列为三峡库区二期专业监测滑坡，自2004年以来，对其地表位移进行持续监测。李远宁，冯晓亮等[3]分析了该区2004年的降雨情况与裂口山滑坡监测位移数据之间的关系，认为较大频率和强度的降雨是滑坡变形的主要诱发因素。

裂口山滑坡发育于侏罗系上统遂宁组紫红色泥岩及泥质粉砂岩组成的平缓层状坡中，为典型的平推式岩质滑坡。国内外专家学者对平推式滑坡的主要特征、平推式滑坡的形成条件、平推式滑坡的致灾机理、平推式滑坡的启动判据以及平推式滑坡的防治措施等方面均进行了较为深入的研究。平推式滑坡的概念最先由张倬元[4]于1985年提出，其特征为：滑坡体主要沿层面滑动，滑动面倾角都很小、近水平，一般小于10°[5]。范宣梅[6]对四川省宣汉天台乡滑坡分析后提出了多级平推式滑坡的概念及其成因机制。在成因机制方面，导致平推式滑坡失稳的主要因素为地下水的作用。殷坤龙等[7]研究了万州区近水平地层滑坡，指出诱发平推式滑坡的主因是静水压力。黄润秋[8]指出平推式滑坡的产生，主要由于特定类型的斜坡结构具有间歇裂隙充水承压型水动力特征。舒中潘等[9]认为暴雨是诱发平推式滑坡的重要因素，暴雨所致的后缘静水压力是平推式滑坡体启动的关键因素。周应华等[10]认为水平砂泥岩互层状岩体在上覆岩层自重的作用下，由于水平方向变形不协调，砂岩将受应力而产生裂缝，容易产生平推式滑坡。吉随旺等[11]指出近水平软硬互层斜坡暴雨期间在裂隙水和渗流水的扬压力联合作用下，产生滑移。

平推式滑坡后缘拉裂槽内的临界水头高度的研究，对其稳定性的判断至关重要[12-16]。张倬元[4]通过力学分析推导出了该类滑坡启动的临界水头高度计算公式。范宣梅等[6]通过物理模拟再现滑坡变形破坏过程，进一步验证了张倬元等提出的平推式滑坡启动判据公式。赵勇[17]运用偏最小二乘法回归分析获得了平推式滑坡滑动时临界水头统计模型，并与力学分析得到的启动判据模型进行了对比。刘才华等[18]通过分析张裂隙充水高度和降雨强度的关系，提出了以临界降雨强度作为水力驱动型边坡顺层滑移失稳的判据。

本文通过改变裂口山后缘拉裂缝中的水压力条件，分析其滑面孔隙水压力分布特征，以及有效应力特征，通过综合位移和强度折减法分析，研究了该滑坡的水压力条件对其变形及稳定性的影响。

1 裂口山概况

1.1 基本概况

裂口山滑坡位于云阳县莲花乡长江干流北岸斜坡上。该滑坡在平面上近似矩形(图1)，剖面上呈折线型(图2)，纵长约300 m，前缘宽约380 m，面积1.14×105m2，体积约3.42×106m3。该滑坡左右两侧边界均为沟谷地貌，前缘为基岩陡崖，临空条件较好。后缘为凹形地貌，形成一条大冲沟，将后缘两侧分割成两个独立的基岩山脊。平行于后缘走向发育有一条长约300 m宽约20～30 m的大裂谷，将整个山体“劈开”(图3)，形成裂口山滑坡。裂口山滑坡体后缘两侧宛如两座脱离母岩的“山峰”，两侧高，中间低。滑坡体后部地形较陡，坡度约为30°～35°，中部及前部较为平缓。

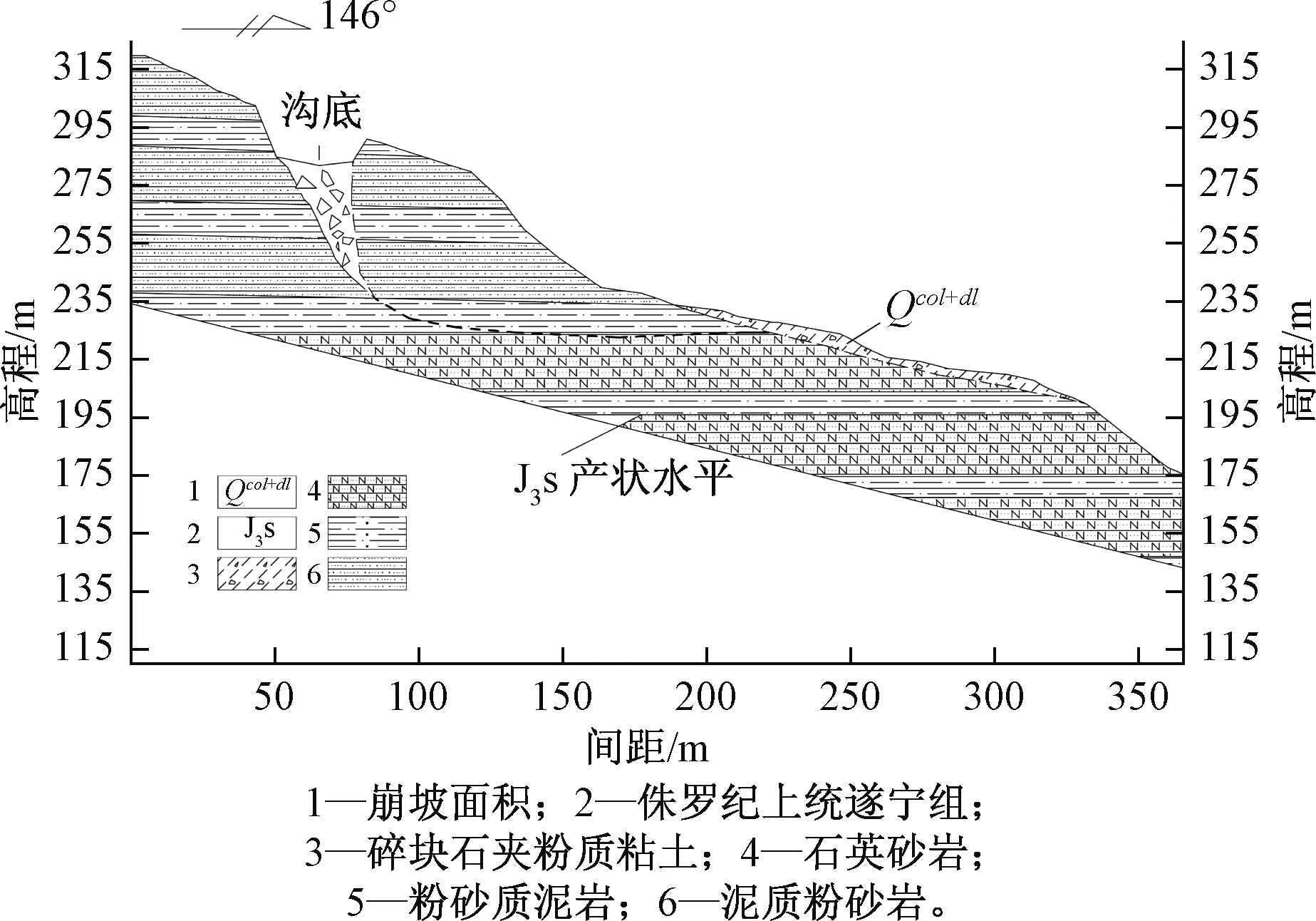
图2 裂口山滑坡地质剖面图Fig.2 Profile of the chasm mountain landslide

图3 裂口山滑坡后缘开裂情况Fig.3 The chasm at Trailing edge

从剖面上看，该滑坡后缘裂口可见深度约为15 m，底下为崩坡积物所填充，据前人资料记载及现场勘查估计，裂口被填充的深度约40 m，裂口张开度最宽处位于顶部，约达30 m。整个滑体坐落于基岩滑床之上，滑床基岩为侏罗系上统遂宁组细粒长石石英砂岩与粉砂质泥岩不等厚互层，以砂岩为主，岩层产状近水平(图4)。滑体主要由侏罗系上统遂宁组薄层细粒长石石英砂岩、泥质粉砂岩与粉砂质泥岩组成，砂泥岩互层，中度风化，强度较低，产状近水平。裂口内由碎块石土所填充，填充深度约为40 m。滑坡体前部表层覆盖第四系滑坡堆积物与崩坡积物，厚约2～5 m，主要由紫红色粉质粘土夹碎块石构成，结构松散。滑带为薄层粉砂质泥岩，主滑面后部产状大致为160°∠60°，前部产状近水平，在地下水浸泡下水解软化，裂口山滑体即沿着此软弱结构面发生蠕滑变形。

研究区内属亚热带暖湿季风气候区，降水充沛。多年平均降水量为1 145.1 mm，夏半年雨季(5～10月)降水量占全年的79%，而冬半年(11月～4月)仅占21%。在连续降雨或暴雨情况下，雨水在裂口山以上多以面流形式向后缘大冲沟内汇聚，然后排向后缘拉裂槽内。在前缘公路附近，可见一两处季节性渗水点，表现为土壤潮湿现象，未见明显水流。

图4 后缘壁面薄层砂泥岩互层Fig.4 Thin sand-shale interbed on the rear wall

1.2 监测数据分析

裂口山滑坡为三峡库区二期专业监测滑坡，滑坡体上共设置3个监测剖面，分别位于滑体的左、中、右侧，每个监测剖面上均安装3个GPS监测点，分别位于滑体后部、中部及前部，共9个GPS专业监测点(图5)。

根据GPS专业监测结果，结合该区历年降雨资料，(从2004年10月份至2013年12月份，每月分上、中、下三旬为累积降雨量计时单位)绘制了该滑坡在2004年10月份至2013年12月份期间的位移—降雨—时程曲线图(图5)。由监测位移曲线可看出，监测点YY08和YY09两点的水平累积位移最大，分别为382 mm和395 mm；水平累积位移最小的点YY01，为79 mm；其它各点的累积位移值位于130～200 mm区间内。监测数据表明，裂口山滑坡各点水平位移呈逐步增大趋势，整体大致沿160°方向运动，处于蠕滑变形阶段。

从空间分布来看，滑坡后缘裂口始于后缘右侧，从西到东逐渐开张，并沿右侧边界贯通至前缘公路，呈东宽西窄的形态；由累计位移曲线可知，滑坡体东部(监测点YY07、YY08、YY09)位移明显大于西部(监测点YY01、YY02、YY03)，滑坡的位移变化趋势与裂口的发育程度呈一致关系，由此推测，滑坡后缘裂口发育深度亦是东部大于西部。

根据位移—降雨—时程曲线，在2007年5～7月期间，各监测点的累积位移曲线呈现不同程度的跳跃式增长，结合降雨曲线可明显发现，发生位移跳跃点时值云阳地区雨季时期，旬降雨量达到了150 mm左右，故初步认为降雨对本次变形起到了很大的激励作用。其中位于滑坡体东部的YY08和YY09两点跳跃现象最为明显，月位移量分别达到80 mm和100 mm，而位于滑坡体西部的监测点YY01、YY02月位移量均在30 mm左右，明显小于滑坡体东部的位移量。同样的现象也出现在2009年7～9月份以及2013年的5～7月份。据现场勘查发现，滑坡左侧前缘崩坡积物堆积厚度相对较大，碎石含量较高，人类旱地耕植，坡脚公路开挖，形成高约4 m的陡坎，并在公路内侧排水沟内有泉水渗出，流量很小。在2007年7～9月份强降雨条件下，堆积层与下伏滑体交界面处的土体在后部陡坡坡面排水的浸透作用下，力学强度下降，局部稳定性减小，加之前缘人工切坡卸荷，促使该处滑体发生局部位移突变(YY08、YY09所处位置)，并在每年雨季均有一定的变形加剧。

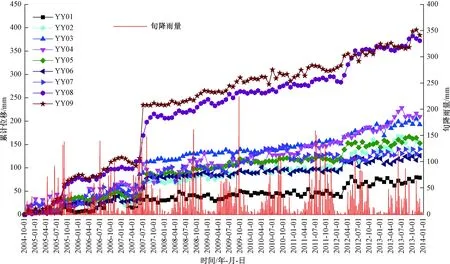
图5 累积位移—降雨量—时程曲线Fig.5 The cumulative displacement-rainfall-time history curve

分析认为，由于东部滑坡后缘裂缝的深度大于西部，在持续降雨条件下，东部裂缝的充水高度大于西部，故裂隙水以及渗流水对滑坡体产生的扬压力亦是东部大于西部，因此导致降雨对滑坡位移变形的激励作用产生了东西部差异之别，使得裂口山滑坡发生了顺时针方向的扭转变形。

2 离散元模型

为进一步研究降雨入渗所产生的水压力对裂口山滑坡变形及稳定性的影响，本文采用三维离散元软件最新版3DEC 5.0，对该滑坡在不同水文地质条件下的工况进行数值模拟计算。3DEC软件采用的是离散单元法，将模型划分为多个块体，块体与块体之间通过角、面或边进行接触，并可以平移、转动或者变形，连接块体之间的节理面可以被压缩、分离、滑动[19-20]。

该软件运用流固耦合原理，可以模拟岩体裂隙水的渗流及水压力的变化情况，还可以模拟裂缝的变形扩展过程，适用于本文裂口山滑坡模型的研究。后缘裂缝充水后，会对滑坡后部产生一定的静水压力，同时在滑体底部产生的扬压力使得滑面的抗剪强度下降，引起滑体产生向前推移变形，进而使得裂缝进一步扩张，充水后产生的水压力变大，又进一步促使位移变形的发生，如此循环耦合作用，直至达到稳定状态。此次研究并未考虑裂缝水渗入滑体、滑床转化为承压水或潜水后的滑坡稳定性的影响。

2.1 计算模型

根据裂口山滑坡地质模型，建立离散元渗流稳定性计算模型(图6)。模型长270 m，高167 m，分为4个区域，1号区域为滑坡后缘以外的岩体，该区岩性为薄层砂岩与泥岩互层；2号区域为裂口内的填充物，主要为碎块石土，夹大块石；3号区域为裂口山滑体，该区岩性为薄层砂岩与泥岩互层，由于曾发生过较大变形及应力释放，该区岩体强度较1区低；4号区域为滑床基岩，岩性为厚层长石石英砂岩，其力学强度较1、2、3区高。

设2号区域与1、3号区域的接触面为1号接触面，该接触面为碎块石土与岩体接触；1号区域与3号区域的接触面为2号接触面，该接触面为岩体裂隙面；3号区域与4号区域的接触面为3号接触面，该接触面夹有软弱泥岩。

裂口填充深度为40 m，即1号接触面垂直高度为40 m。依据计算要求，在1号接触面上设置7个定水头(图中1号接触面处的刻度)，分别为10 m、15 m、20 m、25 m、30 m、35 m、40 m，以研究裂缝水头高度对裂口山变形及稳定性的影响规律。

根据计算精度和计算效率需要，模型各个区域的单元网格划分尺寸不同，1号区域网格尺寸为5 m，2、3号区域网格尺寸为3 m，4号区域网格尺寸为8 m。模型前后边界均固定水平位移为零，底部边界固定水平及竖直方向位移为零。在2号接触面和3号接触面上设置5个监测点，以记录在计算过程中接触面上的水压力及有效应力的变化情况。

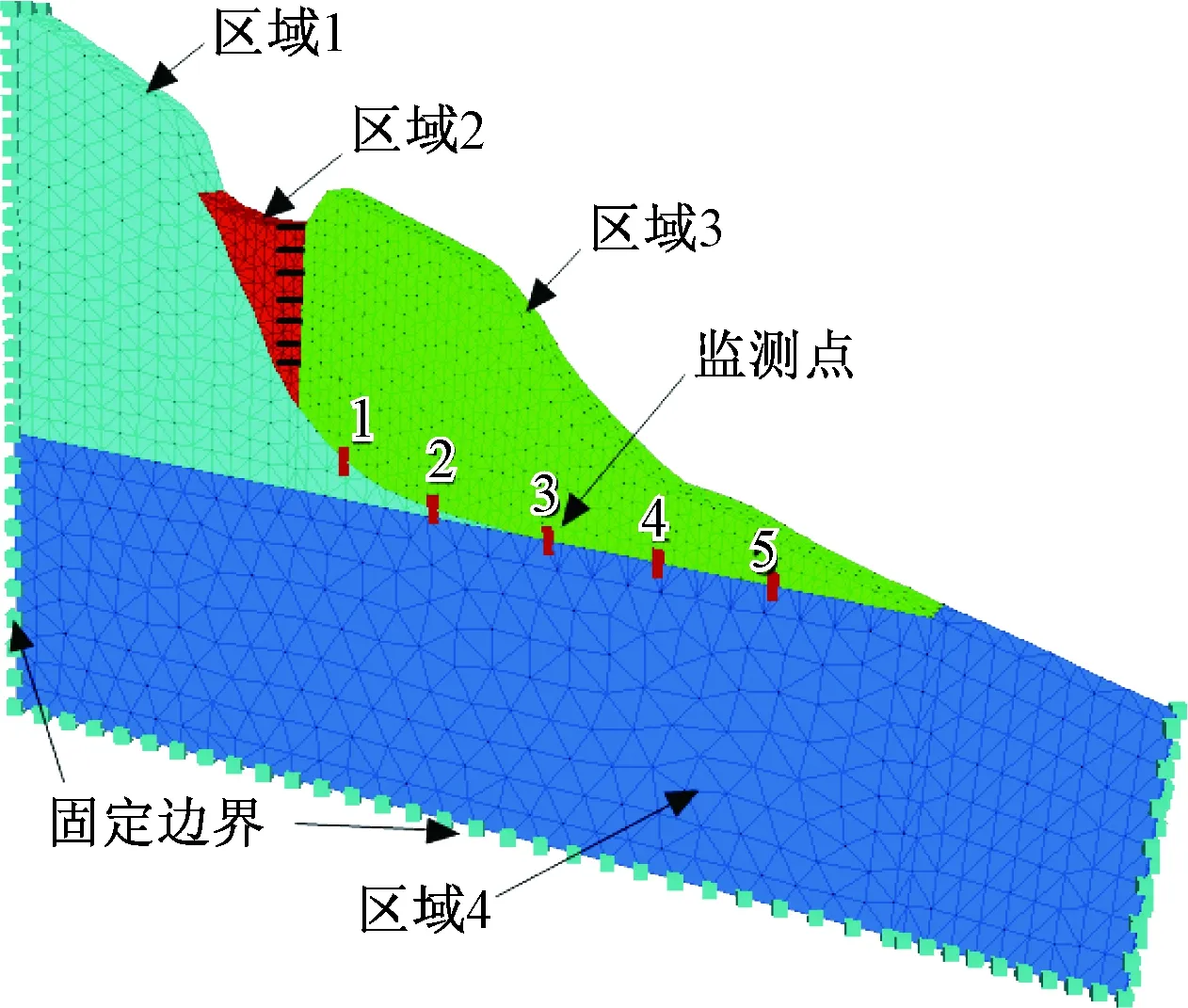
图6 裂口山滑坡计算模型Fig.6 Calculation model of landslide

2.2 计算参数

模型物理力学强度参数分为区域块体材料参数(表1)和接触面参数(表2)，其中在考虑不同静水压力工况条件时，认为在后缘充水条件下滑带土基本处于饱和状态，含水量保持不变，故其滑面力学参数保持不变。区域块体材料采用弹塑性本构模型，接触面采用库伦滑移本构模型。块体的力学强度参数源于室内试验和参数反演综合取值，接触面的力学强度参数源于反演分析。

表1 区域块体力学参数

表2 接触面力学参数

2.3 计算方案

本文主要研究裂口山滑坡的裂缝充水高度对其变形、应力及稳定性的影响规律，如前文所述，在裂缝内施加不同的定水头，计算7种水头工况，每种工况的计算步骤如下：

(1)在施加水头压力之前，先计算模型初始平衡，该阶段共计算10 000步时；

(2)在1号接触面上施加定水头，水体向2、3号接触面入渗，该阶段为流固耦合过程，共计算1 000 000步时；

(3)在已有计算结果的基础上，通过强度折减法，计算滑坡模型的稳定系数。

3 计算结果分析

裂口山滑坡后缘裂缝中的水体，一方面产生静水压力，对滑体施加向前的推力，另一方面，在水体自重及水压力作用下，向下渗流，入渗到底部滑动面的裂隙中，产生扬压力。本文分别从变形、应力和稳定性等方面研究不同水头高度的水压力对裂口山滑坡的影响。

3.1 位移

见图7(a、b、c、d)，分别为裂缝水头H=10 m、20 m、30 m、40 m条件下的滑坡水平位移云图，限于篇幅，本文只列出此四种水头条件下的位移云图。从计算结果可知，受水压力作用，滑体底部水平位移明显大于顶部；且后缘裂缝内水头越高，滑体整体水平位移越大；在水头H=10 m时，位于滑体底部的最大局部水平位移为0.111 m，在水头H=40 m时，位于滑体底部的最大局部水平位移为0.387 m。

图7 不同水头条件下的水平位移云图Fig.7 Displacement nephogram under the condition of different water heads

为了进一步探究裂缝充水高度与滑体所产生水平位移的相关关系，本文将滑体水平位移云图进行量化处理，引入“综合水平位移”的概念，其计算方法如下：

(6)

其中:W——综合水平位移；wi——云图中第i种颜色代表的位移的平均值；ki——第i种颜色的面积与滑体总面积的比值。

本文计算了7中水头工况下滑体的综合水平位移(图8)，按照水头从低到高的顺序，滑体综合位移分别为0.091m、0.121m、0.178m、0.235m、0.275m、0.304m、0.329m。从图8可知，裂缝水头H与综合水平位移W的函数曲线呈三次幂函数形式，其拐点位移H=25 m附近。即水头H在25 m附近变化时，对滑体综合水平位移影响最为敏感。

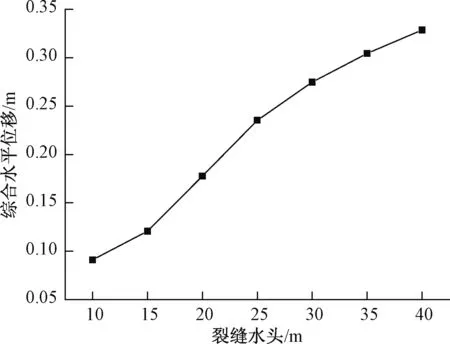
图8 综合水平位移与裂缝水头关系曲线Fig.8 The comprehensive horizontal displacement vs water head

3.2 水压力与有效应力

位移是力的作用结果，水压力不仅会对滑体直接产生位移，而且还会改变滑体的有效应力条件，从而间接地改变滑体位移，亦会影响滑坡体的稳定性。本文在该滑坡滑动面上设置了5个监测点，以记录水压力与有效正应力随时间的变化规律，以及最终达到平衡状态后，两者的大小关系。

通过分析7种不同工况下的水压力随时间的变化规律，发现各工况的规律基本一致，限于篇幅，本文只列举了水头H=25 m时各监测点的水压力随时间的变化曲线(图9)。从滑面各点水压力监测曲线可知，监测点1、2、3在第500 000步时的时候，其水压力就基本已经达到平衡，监测点4、5在第5 000 000步时的时候，其水压力已基本接近平衡。从图9可知2、3号监测点处的水压力最大。

图9 各监测点水压力随时间变化情况(H=25 m)Fig.9 The water pressure monitored changes with time

为进一步分析在不同裂缝水头条件下各监测点的水压力与有效正应力的大小，本文表3中列举了在第5 000 000步时的时候(水压力基本平衡)，各点水压力与有效正应力的最终值，其中裂缝水头H=0为不考虑水压力条件下的计算值(表3)。分析表中数据，可总结出如下几点：

(1)从表中各监测点在不同水头条件下的水压力值可知，当滑面处水压力达到平衡状态后，后缘裂缝水头高度的变化对滑面各点最终水压力大小无明显影响。

(2)从H=0时1号监测点的有效正应力来看，其值为0，说明在滑体及后缘裂缝中填充物的自重力条件下，1号监测点处已处于架空状态。在考虑后缘裂缝充水条件下，2号监测点处的有效正应力从原来的6.52E+05Pa降低至0，即该处的抗剪强度降低至0。

(3)在后缘裂缝充水前后，滑面处的有效正应力变化较大，其中2号监测点处降低至0，3号监测点处降低至充水前的54%，4号监测点降低至原来的28%，5号监测点降低至原来的53%。从各点各水头高度的有效正应力来看，当后缘充水后，水头高度的变化对滑面处有效正应力的大小影响不大。

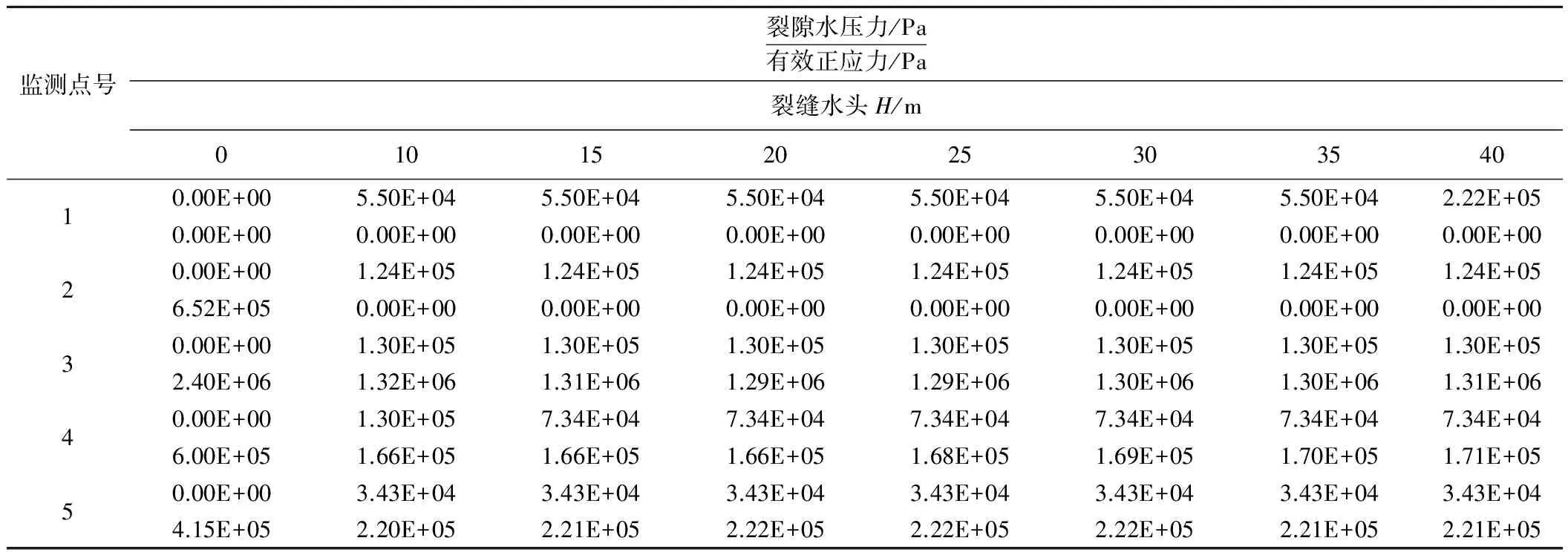
表3 不同水头条件下各监测点的水压力与有效正应力(step=5 000 000)

3.3 稳定性状态

本文在流固耦合计算达到平衡状态后，在此基础上采用强度折减法计算不同水头工况下滑坡模型的稳定系数。在未考虑裂缝充水条件下，滑坡稳定系数Fs=1.67。在充水后，随着水头高度的增加，稳定系数依次减小，分别为1.66，1.65，1.62，1.57，1.50，1.49，1.48(图10)。从各水头的稳定系数变化来看，在H=25 m附近，水头高度的变化对滑坡稳定系数影响较大；在H>30 m，滑坡稳定系数受水头高度的影响较小。

图10 裂缝水头与滑坡稳定系数Fig.10 The stability coefficient vs water head

从整体稳定性来看，在后缘裂缝充水后，滑坡均处于稳定状态，且在最高水头条件下，滑坡稳定系数较未充水状态减小0.18，由此可见，裂口山滑坡后缘裂缝中水压力条件对该滑坡稳定性略有影响，但影响不大。从本文的计算结果可知，裂口山滑坡后缘裂缝水压力条件并非是该滑坡启动的决定性因素，只是促进了其变形，降低了滑面抗剪强度。

裂口山滑坡产生发育由来已久，其所处位置地质构造为巴堰峡系方斗山背斜，该构造的北延部分形迹在近挽期缓慢抬升，且受长江下切作用，形成裂口山。由滑坡专业监测数据可知，目前滑坡变形主要以左侧前缘的局部变形为主，该变形在每年雨季发生跳跃，受降雨作用明显，这与前文数值模拟的位移分析结果一致。而滑坡整体处于缓慢蠕滑状态，数值计算结果也显示各工况下滑坡的稳定系数均大于1.40，即均处于稳定状态。

结合滑坡现场勘查结果，滑坡左侧前缘为临空面，后缘裂口向东延伸至此，在暴雨条件下，边界冲沟汇水和地表水快速灌入，致使裂缝内水头快速上升，水压力急剧增加，在裂缝静水压力和基底扬压力的联合作用下，左侧坡体抗剪强度降低，发生局部变形；结合前人研究结果[2]，笔者认为造成滑坡缓慢蠕滑变形是构造余能消散的结果，即应力调整的过程。

4 结论与探讨

4.1 结论

裂口山滑坡结构为典型的平缓层状坡，该滑坡后缘裂口可见深度约为15 m，底下为崩坡积物所填充，被填充深度约40 m，裂口张开度最宽处位于顶部，达30 m。本文通过分析裂口山滑坡的GPS专业监测位移资料，初步判定其变形与降雨入渗存在一定联系，采用离散元程序3DEC 5.0模拟降雨条件下后缘裂缝充水对滑坡变形、应力状态及稳定性的影响，得出如下结论：

(1)裂口山滑坡后缘裂缝充水产生的滑体变形主要表现为局部变形。滑体底部水平位移明显大于顶部；且后缘裂缝内水头越高，滑体综合水平位移越大；水头H在25 m附近变化时，对滑体综合水平位移影响最为敏感。

(2)在稳态渗流条件下，随着后缘水头高度的增加，滑坡的稳定系数有一定的减小，但幅度不大，且均大于1.4，滑体仍能保持稳定状态。

(3)裂口山滑坡砂岩夹薄层泥岩的岩性组合决定了滑坡在差异蠕变作用下，拉裂缝会不断扩展，这也是导致裂口山滑坡局部变形加剧的重要原因；而暴雨条件下裂缝充水形成的瞬间高水压力是滑坡产生局部变形直接原因。

4.2 探讨

此次研究过程中，未考虑裂缝水渗入滑体、滑床转化为承压水或潜水后对滑坡稳定性的影响，有关裂口山滑坡的成因机制有待更深一步的研究。

[1] 李世海,刘天苹,刘晓宇. 论滑坡稳定性分析方法[J]. 岩石力学与工程学报, 2009, 28(S2): 3309-3324. LI Shihai，LIU Tianping，LIU Xiaoyu. Analysis method for landslide stability[J]. Chinese Journal of Rock Mechanics and Engineering, 2009, 28(S2): 3309-3324.

[2] 茹锦文,王珽. 论线性构造对长江(奉节—忠县段)河谷形态及大型滑坡的控制意义[J]. 中国岩溶, 1990, 9(2): 65-74. RU Jinwen, WANG Ting. Controlling effect of lineament on river valley geomorphology and huge landslides along the yangtze river[J]. Carsologica Sinica, 1990, 9(2): 65-74.

[3] 李远宁,冯晓亮. 长江三峡水库区云阳县典型滑坡变形监测分析[J]. 中国地质灾害与防治学报, 2006, 17(2): 57-60. LI Yuanning, FENG Xiaoliang. Analysis on the deformation of typical landslides at Yunyang countyin the Three Gorges Reservoir region based on monitoring data[J]. The Chinese Journal of Geological Hazard and Control, 2006, 17(2): 57-60.

[4] 张倬元，王士天，王兰生.工程地质分析原理[M].北京: 地质出版社，1994:377-380. ZHANG Zhaoyuan, WANG Shitian, WANG Lansheng. Engineering geology analysis principle[M]. Beijing: Geological Publishing House, 1994:377-380.

[5] 范宣梅，许强，张倬元,等. 平推式滑坡成因机制研究[J]. 岩石力学与工程学报, 2008, 27(S2): 3753-3759. FAN Xuanmei，XU Qiang，ZHANG Zhaoyuan, et al. Study on genetic mechanism of translational landslide[J]. Chinese Journal of Rock Mechanics and Engineering, 2008, 27(S2): 3753-3759.

[6] 范宣梅. 平推式滑坡成因机制与防治对策研究 [硕士学位论文][D]. 成都：成都理工大学，2007. FAN Xuanmei. Study of genetic mechanism and control countermeasures of translational landslide[M. S. Thesis][D]. Chengdu：Chengdu University of Technology，2007.

[7] 殷坤龙，简文星，周春梅，等. 万州区近水平地层滑坡和堆积体成因机制与防治工程研究[R].武汉：中国地质大学，2005：153-154. YIN Kunlong，JIAN Wenxing，ZHOU Chunmei，et al. Study on the mechanism of the translational landslide in Wanzhou district and its prevention project[R]. Wuhan：China University of Geosciences，2005：153-154.

[8] 黄润秋. 20世纪以来中国的大型滑坡及其发生机制[J].岩石力学与工程学报，2007，26(3): 433-454. HUANG Runqiu. Large-scale Landslides and Their Sliding Mechanisms in China since the 20th Century[J].Chinese Journal of Rock Mechanics and Engineering，2007，26(3): 433-454.

[9] 舒中潘，袁磊，汪竟. 暴雨对四川三台县中新中学滑坡稳定性的影响[J]. 四川地质学报，2009，29(2):178-179. SHU Zhongpan，YUAN Lei，WANG Jing.Influence of rainstorm on stability of the zhongxin middle school landslide in santai county，Sichuan[J].Acta Geologica Sichuan，2009，29 (2): 178-179.

[10] 周应华，邵江，罗阳明. 近水平红层边坡变形破坏的力学机制分析[J]. 路基工程，2006(1): 6-7. ZHOU Yinghua，SHAO Jiang，LUO Yangming.Mechanical mechanism of deformation failure of nearly horizontal red bed slope[J].Subgrade Engineering，2006(1): 6-7.

[11] 吉随旺，张倬元，王凌云，等. 近水平软硬互层斜坡变形破坏机制[J]. 中国地质灾害与防治学报，2000，11(3): 49-52. JI Suiwang，ZHANG Zhuoyuan，WANG Lingyun，et al. The mechanism of deformation and failure for the slope composed of nearly horizontal competent and incompetent intercalated rock mass strata[J]. Chinese Journal of Geological Hazard and Control，2000，11(3): 49-52.

[12] 方贻立,马明,李聪,等. 平推式滑坡致灾机理与减灾方法研究进展[J]. 长江科学院院报, 2013, 30(12): 20-27. FANG Yili，MA Ming，LI Cong, et al. Research advances in translational landslide’s mechanism and risk mitigation[J]. Journal of Yangtze River Scientific Research Institute, 2013, 30(12): 20-27.

[13] 刘军, 秦四清, 张倬元. 缓倾角层状岩体失稳的尖点突变模型研究[J]. 岩土工程学报, 2001, 23(1): 42-44. LIU Jun, QIN Siqing, ZHANG Zhuoyuan. Study on catastrophic model with cusp point for failure of stratified rock mass with a gentle inclination[J]. Chinese Journal of Geotechnical Engineering, 2001, 23(1): 42-44.

[14] 赵权利,尚岳全,支墨墨. 平推式滑坡启动判据的修正[J]. 吉林大学学报(地球科学版), 2014, 44(2): 596-602. ZHAO Quanli，SHANG Yuequan，ZHI Momo. Modification of the start-up criterion of translational gliding landslide[J]. Journal of Jilin University(Earth Science Edition), 2014, 44(2): 596-602.

[15] 缪海波,殷坤龙,李远耀. 近水平地层滑坡平面失稳模型与破坏判据研究[J]. 水文地质工程地质,2009，36(1): 69-74. MIAO Haibo, YINKunlong, LI Yuanyao. Study on plane instability model and failure criterion of horizontal-strata landslide[J]. Hydrogeology & Engineering Geology, 2009，36(1): 69-74.

[16] 成国文，李善涛，李晓，等. 万州近水平地层区堆积层滑坡成因与变形破坏特征[J]. 工程地质学报, 2008, 16(3): 304-310. CHENG Guowen, LI Shantao, LI Xiao, et al. Forming causes and deformation-destruction characters of accumulative stratum landslide in horizontal stratum in wanzhou[J]. Journal of Engineering Geology, 2008, 16(3): 304-310.

[17] 赵勇,许模,赵红梅. 平推式滑坡后缘启动水头探讨[J]. 人民长江，2011,17:32-36. ZHAO Yong，XU Mo，ZHAO Hongmei. Discussion on starting water head in trailing edge of translational landslide[J]. Yangtze River，2011,17:32-36.

[18] 刘才华，徐健，曹传林，等.岩质边坡水力驱动型顺层滑移破坏机制分析[J].岩石力学与工程学报，2005，24(19): 3529-3533. LIU Caihua，XU Jian，CAO Chuanlin，et al.Analysis of bedding-slip failure mechanism of rock slope due to hydraulic drive [J].Chinese Journal of Rock Mechanics and Engineering，2005，24(19): 3529-3533.

[19] Cundall P A. A computer model for simulating progressive large scale movements in blocky rock systems[A]. Proceedings of the International Symposium Rock Fracture，ISRM[C]. 1971:1-8.

[20] Cundall P. A. The measurement and analysis of acceleration on rock slopes[D]. London:University of London，Imperial College of Science and Technology，1971.

The numerical simulation on landslide stability to chasm mountain landslide affected by water filling at trailing edge chasm

DU Changjian1,2,YI Qinglin1,2,3，ZHANG Mingyu1,2,MENG Huikun1,2,WEN Kai1,2

(1.CollaborativeInnovationCenterforGeo-HazardsandEco-EnvironmentinThreeGorgesArea,Yichang,Hubei443002,China; 2.MinistryofEducationKeyLaboratoryofGeologicalDisasterofThreeGorgesReservoirArea,ChinaThreeGorgesUniversity,Yichang,Hubei443002,China;3.NationalFieldObservationandResearchStationofLandslidesInThreeGorgesReservoirAreaofYangtzeRiver,ChinaThreeGorgesUniversity,Yichang,Hubei443002,China)

The displacement data of professional GPS monitoring of chasm mountain landslide is analyzed, to preliminary assume the relationship between deformation and rainfall infiltration. Under the condition of water filling in the back edge crack, the deformation, stress state and stability is simulated through the discrete element method, to study the effect of water pressure on chasm mountain landslide. The results show that the deformation caused by the water pressure in trailing edge chasm is mainly local, and the horizontal displacement at the bottom of the sliding body is significantly greater than the top, and the higher the water head at trailing edge chasm, the comprehensive horizontal displacement is larger. The comprehensive horizontal displacement is the most sensitive when the water head variation Around 25 meters. The thrust produced by water in trailing edge chasm is not enough to make the landslide. Before and after water filling in the trailing edge chasm, the effective normal stress on sliding surface reduce a lot, while the stability of the whole landslide changes slightly. So the chasm mountain landslide could keep stable state no matter the water head in trailing edge chasm.

the chasm mountain landslide; chasm; water head; deformation; stress state; stability

10.16031/j.cnki.issn.1003-8035.2017.01.03

2016-06-13;

2016-10-21

三峡大学研究生创新研究基金项目(2015CX032)

杜常见(1990-)，男，硕士研究生，主要从事地质灾害防治及岩土工程方面的研究。 E-mail:805529170@qq.com

易庆林(1966-) ，男，教授，主要从事防灾减灾工程、变形监测等方面的研究。 E-mail: yiqinglin@ctgu.ed

P642.22

A

1003-8035(2017)01-0013-09