基于下沉等影响原理的倾斜煤层开采沉陷预计方法及应用

田国灿，徐乃忠，高 超

(1.煤炭科学研究总院 开采研究分院，北京 100013；2.天地科技股份有限公司 开采设计事业部，北京 100013)

基于下沉等影响原理的倾斜煤层开采沉陷预计方法及应用

田国灿1,2，徐乃忠1,2，高 超1,2

(1.煤炭科学研究总院 开采研究分院，北京 100013；2.天地科技股份有限公司 开采设计事业部，北京 100013)

通过对以往开采沉陷的预计算法进行分析，采用下沉等影响原理建立沉陷预计的模型，设计适用于任意形状工作面的开采沉陷预计程序。该程序采用C#语言编写，进一步优化了工作面各角点坐标和最终计算结果的处理，并通过对计算区域采用三角形划分法的对比得知本模型可以进一步消除倾斜煤层在开采下沉计算中由采深的变化所带来的误差，为倾斜煤层的预计提供了更为准确的计算方法。

下沉等影响原理；倾斜煤层；开采沉陷；C#语言；概率积分法

地表沉陷预计是矿山开采沉陷学的重要内容之一，对开采沉陷的理论研究和生产实践均具有重要意义[1]。在理论上，利用预计的结果可以定量地分析研究受开采影响的地表在时间上和空间上的分布规律。为了提高开采沉陷预计的准确性，有必要对预计方法所采用的理论模型、预计参数与地质采矿条件之间的定量、定性关系进行深入地研究，从而能更进一步地加深对开采沉陷基本规律的认识。在生产实践上，利用开采沉陷预计结果可以对“三下”(建筑物下、铁路下和水体下)的开采活动进行技术指导[2]。

因此，在借鉴已有理论体系的基础上，应用下沉等影响原理和概率积分法的基本理论，开发一个能对任意形状的倾斜工作面进行处理并具有足够高精度的开采沉陷预计程序十分必要[3]。

1 程序设计技术路线

在开发环境方面，C#作为目前主流的编程语言之一，既继承了C++语言的强大功能，又有VB的快速编写方式，对于构建系统界面具有无可比拟的优势。既可以保证快速、稳定地构建应用程序，又能在进行开发的时候调用现有的、无论是什么语言编写的COM对象，具有极强的交互性。因此决定采用C#语言来完成系统框架的构建[4]。系统整体构架见图1。

如图1所示，程序的运行首先需要获取工作面的相关信息，工作面各角点的坐标不再需要手工录入，可通过对CAD组件的调用实现直接对任意形状的多边形进行角点坐标捕捉。

地质采矿条件参数的输入包含煤层采高、工作面最大采深、工作面煤层倾斜方向、煤层倾角、下沉系数、主要影响角正切、水平移动系数、开采影响传播角以及上山、下山、开切眼边界、停采线边界的拐点偏移距。

初始参数设置完之后对所有角点进行沿重心的坐标旋转，使走向方向沿X轴正方向，倾向沿Y轴正方向，以便于随后求得沿走向或倾向的地表移动变形值。然后通过设计好的预计模型对所要预计的影响范围、任意剖面或任意点的移动变形进行计算，并对计算结果的坐标点再次进行坐标旋转，以达到与原坐标系相匹配的目的。最后对数据进行后处理，生成剖面图或者等值线图。

2 等影响原理的算法实现

目前我国应用广泛且较为成熟的预计方法主要是概率积分法，但由于工作面多边形的不规则性，使得二重积分的上下限难以界定，所以大部分预计模型都是将工作面的不规则多边形切割划分为规则的矩形来进行叠加运算。即使有国内学者提出从工作面坐标原点出发(如图2中的1角点)分别连接工作面的其他各点，将整个区域划分为若干个三角形并对每个三角形进行二重积分的三角形划分法，以此来确定积分上下限并消除由矩形叠加算法引起的计算误差[5]，但该解决方法依然没有对地表沉陷主要影响半径r值的变化因素进行考虑，只是采用平均采深值将r值设定为一个常量。但在实际开采过程中，倾斜煤层条件下的采深是随着工作面位置的移动在不断变化的，工作面的倾角越大，采用平均采深算法的误差也就越大。因此，有必要建立一个可以对任意形状工作面以及任意煤层倾角进行沉陷预计的模型。

图2 三角形划分法示意

2.1 等影响工作面及相关变量的转换

由沉陷预计概率积分法计算公式，地下坐标点U(x,y)处的单元开采引起地表坐标P(x0,y0)处的下沉值为：

(1)

r=H/tanβ

(2)

式中，r为主要影响半径；H为采空区坐标点(x,y)处的采深；tanβ为地表沉陷预计参数中的主要影响角正切。

在开采区域较大，并且煤层倾角不为0的情况下，采深H值随着煤层的倾向和走向在不断地变化。若图3中A点为最大采深位置，其坐标为(xa,ya)，工作面ABCD上任意一点U(x,y)的采深值则需要由煤层倾角、煤层倾向以及最大采深来计算求得。

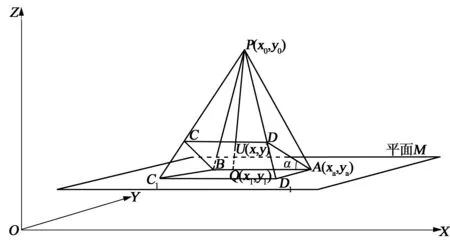
图3 实际工作面与投影工作面

若煤层倾角为α，煤层倾向为θ，最大采深为H0，则开采区域任意点(x,y)的采深H为：

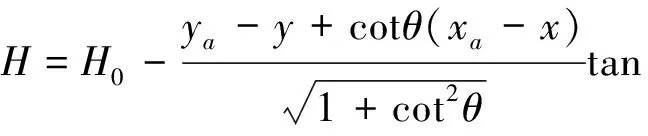
(3)

若将所得的各角点坐标沿逆时针方向旋转(90°-θ)，则新生成的工作面倾向沿y轴正方向，此时θ值为90°，进而消去式(3)中的参数cotθ，同时规范了坐标系，并为之后的预计计算做准备。旋转之后的任意点(x,y)的采深H为：

H=H0-(ya-y)tanα

(4)

将地表点P(x0,y0)与工作面上任意点U(x,y)相连接并延长至最大点采深所在的水平面M得到点Q(x1,y1)，并由图4可知等比关系

图4 工作面点与投影点的坐标关系

(5)

同理

(6)

如果用r1来表示投影至水平面的等价工作面开采主要影响半径，则

r1=H0/tanβ

(7)

将式(4)、(5)、(6)、(7)带入(1)可得

(8)

可以看出投影面上的Q点(x1,y1)与工作面上的U点(x,y)对地表点(x0,y0)的影响是等价的[6]。然后对公式(1)进行面积分得到整个工作面的开采对任意地表点(x0,y0)产生的下沉值：

(9)

式中，wmax为该工作面开采后地表最大下沉值。

对式(9)进行换元并积分可得

w(x0,y0)=

(10)

同时由式(5)、(6)可得

(11)

(12)

最终将式(11)和式(12)带入式(10)中可得

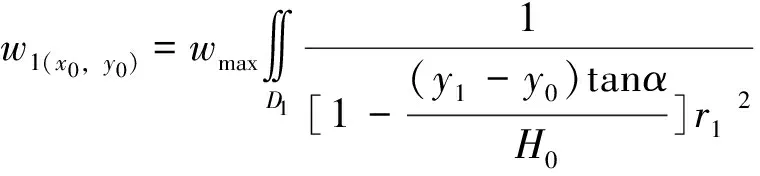
(13)

该式即为转换之后的等价投影面的下沉预计面积分公式，D1为地表任意点(x0,y0)与工作面各角点链接之后投影至最大采深平面的多边形(如图3中多边形ABC1D1)，在新生成的多边形中主要影响半径值为常量，同时每一个要计算的地表点都有与之对应的各不相同的等价投影多边形。

2.2 线积分转化

投影面转换完成D1之后，D1依然是不规则图形，对面积分的上下限进行判定并求取二重积分的算法比较复杂，因此将式(13)转化为线积分对其进行求解。

由数学分析可知，当区域D是一个单连通域，且函数P(X,Y)，Q(X,Y)在D上具有一阶连续偏导数的条件下，则下面等式成立：

这就是线积分和面积分转换的格林公式，其中S为区域D的边界曲线[7-9]。

由式(13)可知r1为常量的情况下对x进行积分相对比较简单，又由高斯误差函数

可知

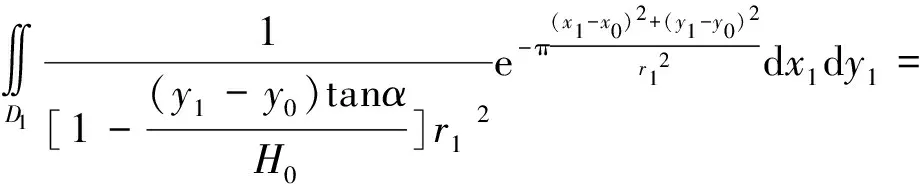
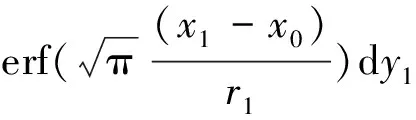
其中区域D1是投影在平面M上的由直线(S1，S2…Sn)所围成的闭合区域，高斯误差函数可以单独进行计算。至此将r值不断变化的二重积分，转换为r值为常量的定积分，在计算过程中，只需将地表点所对应的投影面的各角点坐标计算出来，然后对每一条边进行上式的线积分计算，即可得到与原开采区域D相同的沉陷预计结果。该方法使工作面边界得以确定，并考虑了开采影响范围r值不断变化对地表下沉产生的影响，同时将二重积分等价转化为定积分减少了由计算机计算二次积分所带来的误差[10]。对该式进行相应的求导变换，即可得到倾斜、曲率、水平变形等地表移动变形函数，由于这些函数均为定积分，不存在上下限难以界定的问题，只需沿每条边逐一积分即可得出计算结果，水平移动的计算函数也可通过上述的换元方法最终划为相应的线积分形式，在此不再赘述。

3 程序结构

本程序主要由如下几个模块所组成：

准备模块 录入地质条件参数以及工作面各角点坐标。

地表影响范围计算模块 自动计算开采沉陷影响范围，以2倍的主要影响半径为扩展边界，并确定要计算的地表点坐标。

坐标转换模块 将坐标系统转换为以煤层走向沿x轴正方向，倾向(上山方向)沿y轴正方向。

变形计算模块 结合编写完成的预计模型，将经过左边转换后的各个参数导入，得到任意地表点的移动变形值。

输出模块 生成影响范围内各地表点的地表移动变形值表格并绘制等值线图。

程序结构框图见图5。

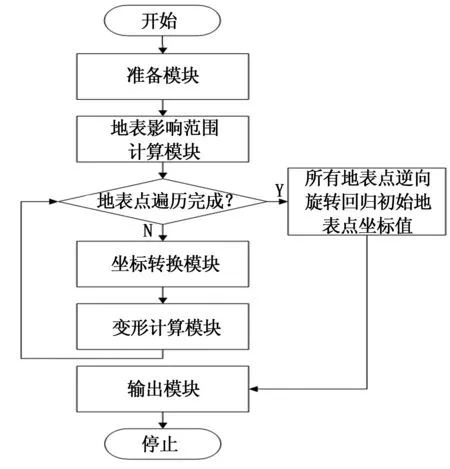
图5 程序结构

4 应用实例

设定一不规则形状工作面，走向长度约1000m，倾向长度约450m，下山方向采深500m，煤层采出厚度3000mm，煤层倾角13°，倾向沿y轴正方向，下沉系数为0.75，主要影响角正切为2.0，最大下沉角90°，水平移动系数0.3，拐点偏移距均为0。将其输入到编写好的沉陷预计程序界面中，并在CAD中获取工作面各角点坐标值。然后用建立好的模型对其进行下沉计算，可得下沉等值线图形，其中多段线为设定的工作面边界，最大下沉值为2146mm。采用将工作面划分为多个三角形的三角形剖分法获得的下沉等值线图形，最大下沉值为2095mm。

将2个等值线图进行叠加对比得到图6。可以看出当考虑煤层倾角所带来的采深变化因素时，相对于三角形划分算法，开采损害影响的边界范围变得较小，但是最大下沉值较三角形划分法的计算结果增大了51mm。

当下沉值越大的时候，下沉等影响算法的影响范围就越为明显地大于三角形剖分法的影响范围。煤层倾角越大，这种变化就会越为明显。这种整体影响范围变小但是一定范围内下沉值变大的变化特点符合倾斜煤层所引起的实际下沉情况，同时也满足主要影响角不变，采深越小影响范围越小的理论。

5 结 论

(1)通过下沉等影响原理，将主要影响半径化为常量，推导出倾斜煤层开采沉陷预计的精确计算公式。

(2)将二重积分形式转换为线积分形式，确定了积分的上下限，进一步简化了积分的过程。

(3)通过编程语言建立了开采沉陷预计模型，并与传统的三角形划分模型进行对比，分析了2种模型得出的不同预计结果。得知本模型更为符合实际情况，同时也使得概率积分法能够更为灵活地应用在倾斜煤层开采沉陷的相关预计与计算当中。

[1]何国清，杨 伦，凌赓娣，等.矿山开采沉陷学[M].徐州：中国矿业大学出版社，1991.

[2]黄乐亭.村庄压煤开采的技术途径[J].中国煤炭，1996(8)：33-35.

[3]王 玲，吴 侃，奚新丽.基于ArcGis Engine的开采沉陷预计系统[J].测绘科学，2008(4)：153-154.

[4]李培现，谭志祥，齐公玉.基于MATLAB的开采沉陷预计系统[J].中国矿业，2008(11)：72-76.

[5]康建荣.任意形多边形工作面多段线开采沉陷预计系统 (MSPS)[J].矿山测量，2000(1)：24-26.

[6]国家煤炭局.建筑物、水体、铁路及主要井巷煤柱留设与压煤开采规程[S].北京：煤炭工业出版社，2000.

[7]张华兴，焦传武.地表移动精确预计法——线积分运算[J].矿山测量，1998(4)：21-29.

[8]周万茂，张华兴，何瑞华.任意形状工作面拐点移动距求取方法[J].煤矿开采，2000(4)：13-16.

[9]张华兴.地表移动与变形的等价转换线积分计算[J].煤矿开采，1991(2)：14-19.

[10]田锦州，徐乃忠，李凤明.误差函数erf(x)近似计算及其在开采沉陷预计中的应用[J].煤矿开采，2009，14(2)：33-35.

[责任编辑：李 青]

Prediction Method and Application of Incline Coal Seam Mining Subsidence Based on Subsidence Principle

TIAN Guo-can1,2,XU Nai-zhong1,2，GAO Chao1,2

(1.Mining Institute，China Coal Research Institute，Beijing 100013，China;2.Coal Mining & Designing Department，Tiandi Science & Technology Co.，Ltd.，Beijing 100013，China)

The past mining subsidence prediction method was analyzed，subsidence prediction model was built based on subsidence principle，mining subsidence prediction program that could be applied any shape working face was designed.The program was designed by C# language，every corner point coordinate of working face and the final results were optimized，the error that induced by mining depth variation in incline coal seam mining subsidence prediction could be eliminated in the model by triangle division method compared in calculated area，and then more accurate prediction method could be provided for incline coal seam prediction.

subsidence principle; incline coal seam; mining subsidence; C# language; probability integrity method

2016-10-27

10.13532/j.cnki.cn11-3677/td.2017.02.017

国家自然科学基金(51604151)

田国灿(1991-)，男，河北衡水人，在读硕士研究生，研究方向为开采沉陷预计。

田国灿，徐乃忠，高 超.基于下沉等影响原理的倾斜煤层开采沉陷预计方法及应用[J].煤矿开采，2017，22(2)：65-68.

TD327

A

1006-6225(2017)02-0065-04