同步磁阻电机混沌系统的有限时间同步控制

雷腾飞, 边惠惠, 代严满, 陈 恒

(1.齐鲁理工学院 机电工程学院， 济南 250200； 2.西京学院 控制工程学院， 西安 710123 )

同步磁阻电机混沌系统的有限时间同步控制

雷腾飞1, 边惠惠1, 代严满2, 陈 恒2

(1.齐鲁理工学院 机电工程学院， 济南 250200； 2.西京学院 控制工程学院， 西安 710123 )

通过对一类同步磁阻电机动力学系统进行混沌动力学的基本分析与研究，提出同步磁阻电机混沌系统的主动-有限时间控制，主动控制用来实现动态误差线性项与非线性项的近似解耦。通过仿真验证了本文所提的控制策略，本文设计的有限时间控制器比传统的控制器具有更强的快速响应能力。

同步磁阻电机; 混沌同步；有限时间

同步磁阻电机又称反应式同步电机，因自身转子上没有励磁绕组，同时也无有转子的损耗，故具有转换效率高、可靠性好等特点，广泛应用于工农业、交通、航空等领域的交流高性能调速系统中[1]。

近年来，随着混沌动力学的发展与完善，科学工作者在激光、电子、机械振动等领域发现了混沌现象[2-9]。电机与机电系统作为一种强非线性、强耦合、动态的复杂动力学系统，备受科研工作者以及工程师们的关注与探索。目前，对于电机系统与机电系统的混沌动力学研究主要集中在永磁同步电机与无刷直流电机系统。由于永磁同步电机与无刷直流电机的模型与经典Lorenz系统非常类似，研究此类电机系统可参考文献也较多[3-7]，而同步磁阻电机的混沌行为研究的文献则鲜少。文献[3]对一类永磁同步电机系统中混沌行为进行了分析，得出了相关参数对系统的影响以及系统的电路实现；文献[4]对一类无刷直流电机进行了动力学分析与数值仿真计算；文献[5]对一类具有阻尼特点的永磁同步风力发电机进行了分数阶的建模与自适应控制，最后利用电路实现所提出的控制方法；文献[6]采用滑模变结构控制对永磁同步电机混沌系统进行了控制；文献[7]提出永磁同步电机混沌系统的同步控制问题，且基于Lyapunov稳定性原理将其控制；文献[8-9]分别采用自适应控制以及自适应滑模控制策略将参数已知与未知下的同步磁阻电机混沌系统加以控制。 目前对于永磁同步电机以及无刷直流电机的混沌同步研究已广泛进行，然而同步磁阻电机系统的混沌同步研究较少，故开展同步磁阻电机混沌同步问题的研究尤为重要。

有限时间控制技术自1986年提出以后，备受国内外学者的普遍关注，并在非线性系统的混沌控制与混沌同步中得以广泛应用[10-13]。文献[10-11]针对几类混沌系统进行了有限时间控制；文献[12]基于有限时间稳定性原理对一类永磁同步电机进行了同步控制；文献[13]针对一类航天器姿态动力学系统，增加了可调节终端吸引子的权数，重新设计了一类新的有限时间同步控制器。

本文针对一类同步磁阻电机的混沌动力学模型，首先利用分岔图、Lyapunov指谱以及相轨迹等分析方法，研究了参数对系统的影响；其次根据有限时间稳定性原理，设计出了有限时间同步控制器，优于文献[13](文献[13]有限时间控制器优点在于具有可调节终端吸引子的权数，而本文设计出的终端吸引子的权数是可自适应调节的)；最后对设计的有限时间控制策略进行了仿真，仿真结果充分说明了控制器的鲁棒性以及快速性，也为研究更为复杂的控制器奠定了基础。

1 同步磁阻电动机混沌系统模型

基于同步磁阻电动机混沌动力学的模型为[8]

(1)

式中：id,iq与ud,uq分别为定子电流与电压的的直轴与交轴的分量；Rs为定子电阻；ωe,ωg分别为电角频率与发电机转速；Ld,Lq分别为直轴与交轴的电感；Jeq为机组等效转动惯量；Φ为永磁磁铁的磁通；Te为转磁转矩；B为发电机的转动粘滞系数。

假设发电机气隙非均匀，d轴与q轴电感量不相等，则经过仿射变换与时间尺度变换得到无量纲的状态模型如下:

(2)

图1 同步磁阻系统(2)的混沌吸引子

2 参数对同步磁阻电机系统的影响

对于同步磁阻电机系统，参数Rs与Φ受电机运行工作时影响最大，表现在模型上即参数c。本文以参数c为主要研究对象，利用Matlab对其作出了参数c变化下的Lyapunov指数图、分岔图如图2所示，从图中易观察出，Lyapunov指数图与分岔图具有一致性。由图2(b)可看出，同步磁阻电机是通过倍周期方式进入混沌状态的(参数由大变小)，参数c=16左右出现了周期窗口，具体参数c变化下的相图如图3所示。

图2 参数c变化

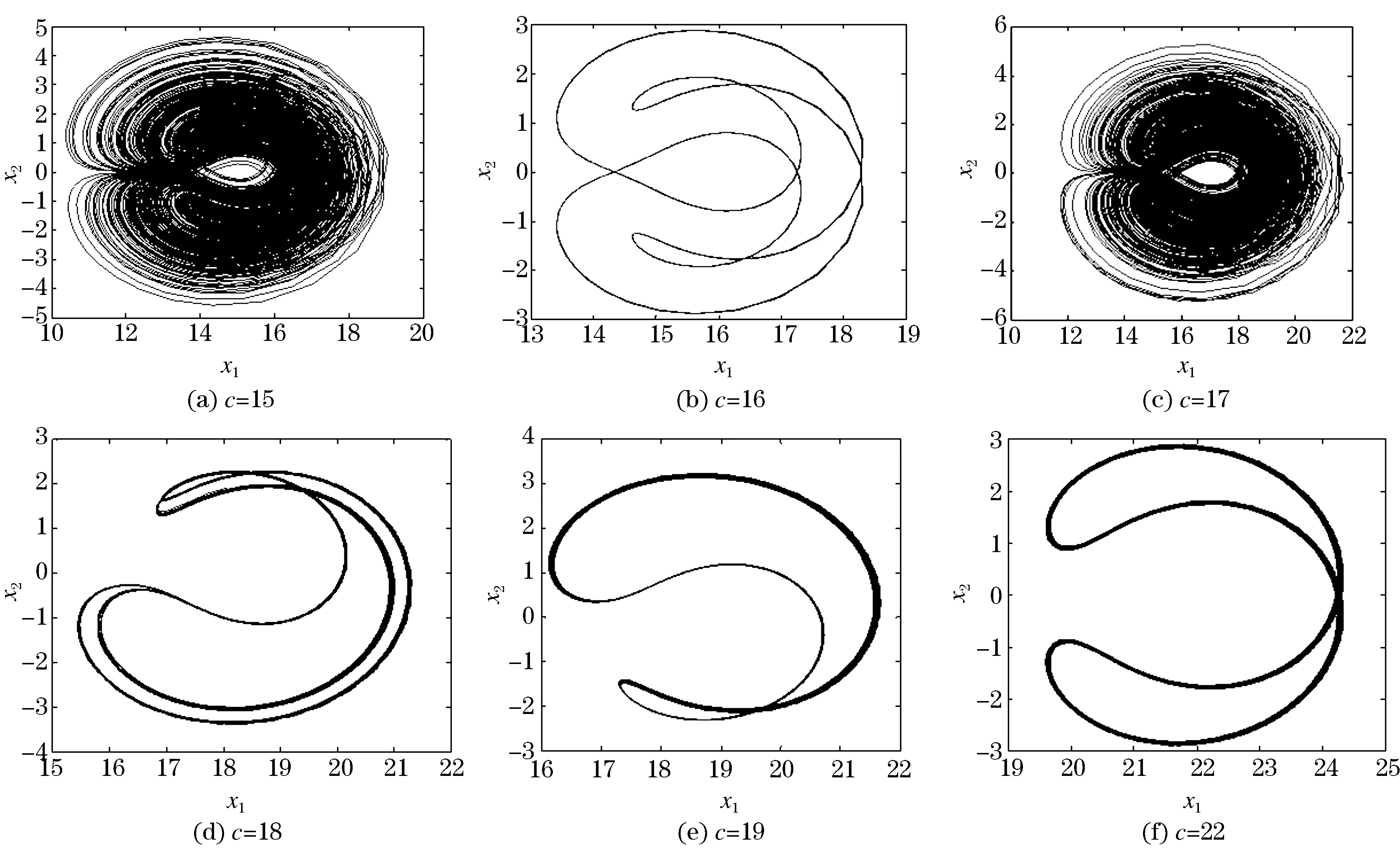
图3 参数c变化下的系统相图

3 有限时间同步控制器设计

考虑同步磁阻电机运行中突然断电的情形，即同步磁阻电机没有带载情况，系统(2)为驱动系统，则响应系统为

(3)

令e1=y1-x1，e2=y2-x2，e3=y3-x3，则误差系统为

(4)

定理1 对于误差系统(4)，基于有限时间稳定性理论，设计同步控制器

(5)

将控制器u2,u3代入误差系统(4)，则

-β2V2

4 仿真研究

因设计的控制器含有吸引子比例系数，比例系统可根据自适应律调节参数g1,g2,g3，从而改变驱动系统(2)与驱动系统(3)同步所用的时间。若令g1=g2=g3=5，其他参数不变，则x1与y1达到同步时间为1s以下，效果更佳，具体仿真结果如图5所示。

从图5可以看出，本文设计的有限时间同步控制器可以在有限时间内快速稳定实现驱动系统与响应系统的同步，而且还可调节控制自适应律的权值参数g1,g2,g3，使其同步时间得以控制。

5 结 语

本文针对一类同步磁阻电机混沌动力学系统，根据有限时间稳定性理论，改进了主动-有限时间控制器，且终端吸引子的权数可自适应，从而实现了系统同步，可以通过改变终端吸引子权数的自适应律权值参数g1,g2,g3改变系统的响应能力。本文控制器具有响应时间快以及稳定性良好的优点，为混沌同步应用于通信保密以及图像加密等领域的研究提供了新的思路与策略。

图4 g1=0.1,g2=g3=5下系统的同步结果与误差结果

图5 g1=g2=g3=5下系统的同步结果与误差结果

[1] GAO Y，CHAU K T.Hopf bifurcation and chaos in synchronous reluctance motor driver[J].IEEE Transaction on Energy Conversion, 2004,19(2):296-302.

[2] WANG Zhen, LEI Tengfei, XI Xiaojian,et al. Fractional control and generalized synchronization for a nonlinear electromechanical chaotic system and its circuit simulation with Multisim[J]. Turkish Journal of Electrical Engineering and Computer Sciences, 2016, 24(3): 1502-1515.

[3] 薛薇，郭彦岭，陈增强.永磁同步电机的混沌分析及其电路实现[J].物理学报，2009,58(12):8146-8151. XUE Wei, GUO Yanling,CHEN Zengqiang．Analysis of chaos and circuit implementation of a permanent magnet synchronous motor[J]. Acta Physica Sinica，2009,58(12):8146-8151.

[4] 杨志红, 姚琼荟. 无刷直流电动机系统非线性研究[J].动力学与控制学报, 2006, 4(1):59-62. YANG Zhihong,YAO Qionghui. Research of non-linearity in brushless DC motor system[J]. Journal of Dynamics and Control, 2006，4(1) : 59 - 62．

[5] 雷腾飞，陈恒，王震，等.分数阶永磁同步风力发电机中混沌运动的自适应同步控制[J].曲阜师范大学学报(自然科学版)，2014，40(3)：63-68. LEI Tengfei，CHEN Heng，WANG Zhen，et al． Adaptive synchronization control of chaotic motion in fractional order permanent magnet synchronous wind generators[J]. Journal of Qufu Normal University(Natural Science)，2014， 40(3): 63-68．

[6] 杨国良,李惠光.直驱式永磁同步风力发电机中混沌运动的滑模变结构控[J].物理学报,2009,58(11):7552-7557. YANG Guoliang，LI Huiguang． Sliding mode variable-structure control of chaos in direct-driven permanent magnet synchronous generators for wind turbines[J]．Acta Physica Sinica,2009, 58(11):7552-7557.

[7] 张兴华,丁守刚.非均匀气隙永磁同步电机的自适应混沌同步[J].控制理论与应用.2009,26(6):661-664. ZHAGN Xinghua，DING Shougang．Adaptive chaotic synchronization of permanent magnet synchronous motors with nonsmooth air-gap[J]． Control Theory & Applications, 2009,26(6):661-664.

[8] 雷腾飞，陈恒，孟敬，等.同步磁阻电机混沌系统的自适应滑模控制[J].黑龙江电力，2015，37(2):130-132. LEI Tengfei，CHEN Heng，MENG Jing，et al．Self-adaptive sliding mode control of chaotic system in synchronous reluctance motor[J]. Heilongjiang Electric Power，2015，37(2):130-132.

[9] 雷腾飞，陈恒，王震，等.同步磁阻电机混沌系统的自适应控制[J].洛阳理工学院学报(自然科学版)，2015,24(4):64-67,77. LEI Tengfei, CHEN Heng, WANG Zhen, et al. Adaptive control of chaos in synchronous reluctance motor[J]. Journal of Luoyang Institute of Science and Technology(Natural Science Edition), 2015, 24(4): 64-67, 77.

[10] WANG H， HAN Z Z，XIE Q Y．et al.Finite-time chaos syschronizationof unified chaotic systems with uncertain parameters[J].Communication Nonliner Science Number Simulation,2009,14(5): 2239-2237.

[11] WANG Hua, HAN Zhengzhi, XIE Qiyue, et al. Finite-time chaos control of unified chaotic systems with uncertain parameters[J]. Nonlinear Dynamics, 2009,55(4): 323-328.

[12] WEI D Q，ZHANG B.Controlling chaos in permanent magnet synchronous motor based on finite-time stability theory[J]. Chinese Physics B,2009,18(4):1399-1403.

[13] 陈恒，雷腾飞，尹劲松. 航天器姿态动力学有限时间的混沌控制[J].徐州工程学院学报(自然科学版)，2016, 31(2): 67-73. CHEN Heng，LEI Tengfei, YIN Jingsong．Chaotic control with finite time of spacecraft attitude dynamics[J]. Journal of Xuzhou Institute of Technology(Natural Sciences Edition), 2016, 31(2): 67-73.

(编辑 陈银娥)

Finite time synchronization control of chaos system in synchronous reluctance machine

LEI Tengfei1, BIAN Huihui1, DAI Yanman2, CHEN Heng2

(1. School of Mechanical and Electrical Engineering, Qilu Institute of Technology, Jinan 250200, China; 2. School of Control Engineering, Xijing University, Xi’an 710123, China)

According to the basic analysis and research of chaotic dynamics on dynamics system of a type of synchronous reluctance machine, the concept of initiative-finite time control in chaotic dynamics of synchronous reluctance machine is proposed in which the initiative control enables approximate decoupling of the linear terms and nonlinear terms of the dynamic errors. By the simulation, the control strategy proposed in this paper is verified and the controller of finite time enjoys a more rapid response capacity than the conventional one.

synchronous reluctance machine; chaos synchronization; finite time

2016-11-18。

齐鲁理工学院科技计划项目(07qlk0012)。

雷腾飞(1988—)，男，硕士研究生，主要研究方向为混沌系统与控制。

TP273+.2

A

2095-6843(2017)02-0149-05