测井电缆衰减特性拟合及其电路建模
2017-05-14闫景富邹庆言刘得军
闫景富, 邹庆言, 刘得军
(中国石油大学(北京), 北京 102249)
0 引 言
连接井下测井仪器和地面设备的不同类型、不同长度、不同厂商生产的测井电缆对信号的衰减特性不尽相同,甚至差别很大。对于电缆两端的硬件设备设计必须考虑所使用的测井电缆对系统数据传输性能的影响。常用的5 000、7 000 m测井电缆体积庞大,价格昂贵,一般研发单位在测井仪器设计完成后没有条件直接在实际电缆上对仪器性能进行测试,通常的做法是事先设计一个数据传输性能与实际电缆特性比较接近的电缆模拟器,借助该模拟器进行室内实验,效果良好后再做进一步现场实验。电缆模拟器与实际电缆传输特性吻合程度的好坏直接影响设备整体的调试和实验进度。设计电缆模拟器首先需要掌握实际电缆的参数或传输特性,常见的方法有理论计算法和测试法[1]。多数情况下,受环境、材料和生产工艺等因素的限制,采用理论计算法得到的参数与实际电缆参数相差较远。本文采用扫频测试法,以电缆在各离散频率点处实测的衰减值为拟合目标,通过传递函数非线性拟合方法为电缆建立电路模型。
1 传递函数的零、极点分布对幅频特性的影响
设系统传递函数H(s)的表达式为
(1)
将式(1)写为零、极点形式,取s=jω,在复平面中s沿虚轴移动,得到
(2)
式(2)分母中任一因子(jw-pi)相当于由极点pi引向虚轴某点jw的矢量;分子中任一因子(jw-zj)相当于由零点zj引向虚轴上某点jw的矢量。用矢量模和矢量角的形式表示后,H(jw)可以写为
|H(jw)|ejφ(w)
(3)
当ω沿虚轴移动,各复数因子(矢量)的模和辐角均随之改变,从而可得到传递函数的幅频特性曲线及相频特性曲线[2]。
2 测井电缆传递函数的求解
2.1 原始数据的预处理
以七芯测井电缆缆芯7和外铠作为信号传输线(即T7模式),通过对某7 000 m电缆一端施加扫频信号、在另一端测量信号幅度的方法发现其衰减特性总体上呈现出随信号频率增大而衰减加剧的规律。频率低于30 kHz时幅度衰减特性变化比较剧烈,且出现上下波动起伏的现象;频率高于30 kHz以后总体呈现单调下降的趋势;频率大于300 kHz时幅度衰减达60 dB以上,不太可能作为信号传输的有效频段。为了更准确、精细地表示在较低频段时电缆衰减特性的变化规律,实测数据在低频段测量点比较密集,较高频段测量点较稀疏。
为满足拟合迭代运算的需要,兼顾拟合准确度,需要对原始非均匀测量数据进行等间隔采样或做插值。以1 kHz为起点,4 kHz为频率间隔对数据进行预处理。处理后电缆衰减特性见图1中折线所示。该折线是由原始测量数据抽样或插值后的数据点连接而成。图1中预处理后的数据仍然可以准确反映原始数据的变化特点。之后的拟合运算均基于预处理后的数据进行。

图1 预处理后数据与原始测量数据对比
2.2 拟合方法介绍及其拟合效果
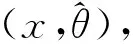
(4)
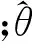
(1) 在MATLAB中新建一个function,把传递函数的模型写到function中,具体程序为
function f=myfun(a,x)
f=(a(1).*x.^4+a(2).*x.^3+a(3).*x.^2+a(4).*x+a(5))./(a(6).*x.^5+a(7).*x.^4+a(8).*x.^3+a(9).*x.^2+a(10).*x+a(11));
end
(2) 利用NLINFIT函数进行拟合,程序为
a0=[1 1 1 1 1 1 1 1 1 1 1];
for i=1:200
a=nlinfit(x,y,@myfun,a0);
a0=a;
end
图2为拟合后传递函数的幅频特性曲线与实验数据之间的对比关系。图2中两者的吻合程度较好。为了定量表示拟合结果与实际数据之间的差异,引入SSE(和方差或者误差的平方和)指标对拟合效果进行评价。SSE的定义为
(5)
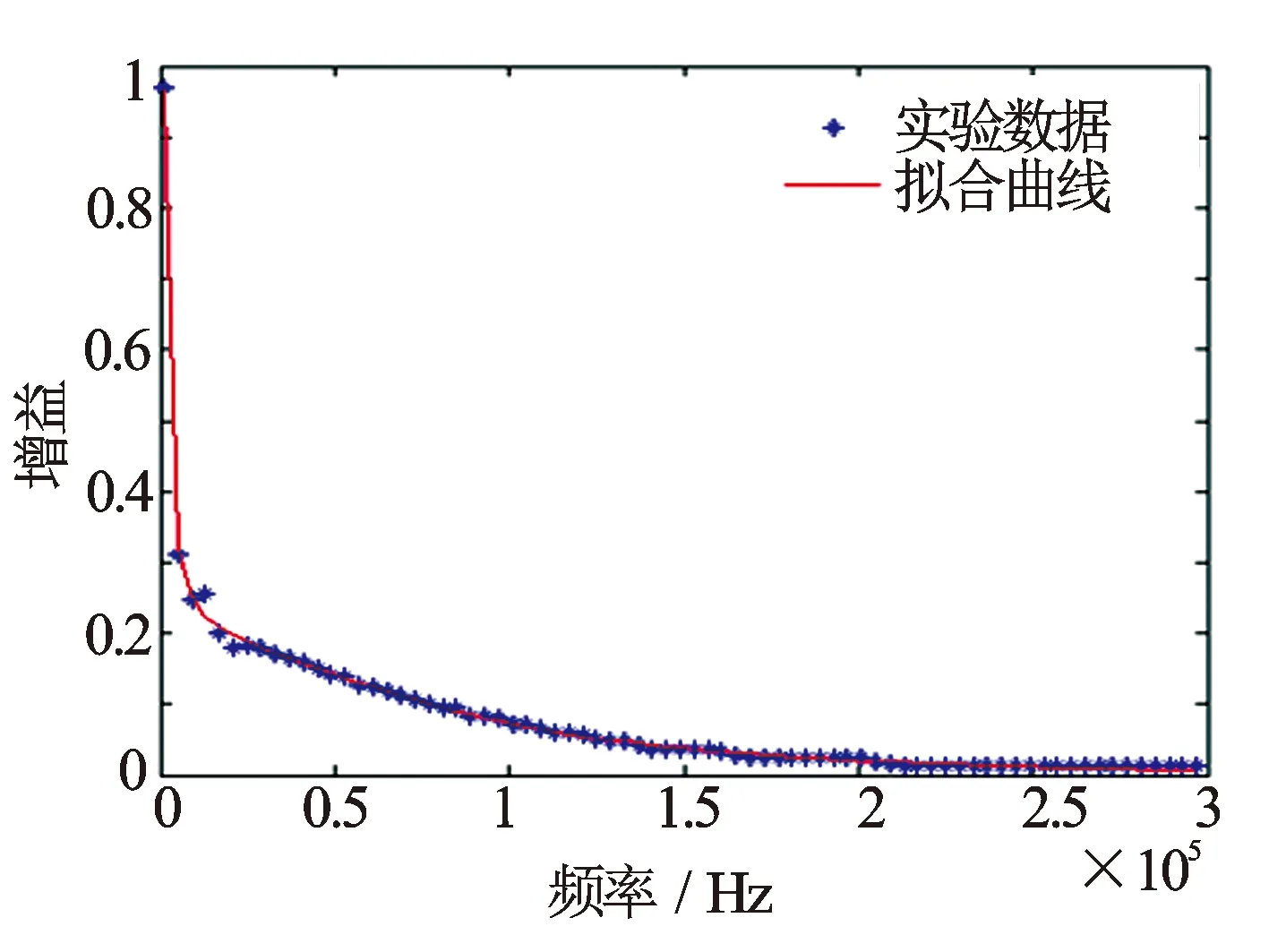
图2 拟合函数的幅频特性与实测数据对比
通过计算,得到设计中SSE值为0.002。表明对预处理后的数据采用NLINFIT函数进行拟合起到了很好的拟合效果。进一步观察发现,即使与最初未经等间隔采样的测量数据对照,其吻合程度也较好。至此,得到所对应的传递函数表达式为
(6)
传递函数中分母多项式的系数存在负数,即有极点位于s域右半平面,表明该系统是非稳定系统,物理无法实现,需要将式(6)右半平面的极点对称到虚轴左半平面,根据零、极点分布与系统频率特性的关系,可知此时系统的幅频特性不会受到影响。经过计算可得最终系统的传递函数为
(7)
3 测井电缆电路模型设计
为了通过传递函数得到相应的电路模型,将式(7)分解为部分分式展开和的形式
(8)
式(8)最后一项的系数和前几项相比很小,在设计模拟电路时可以忽略,只需考虑H(s)前3项。其中,第1项为二阶系统,第2项和第3项为一阶系统。一阶、二阶传递函数分别可由一阶、二阶电路实现。图3为常用的电路模型。
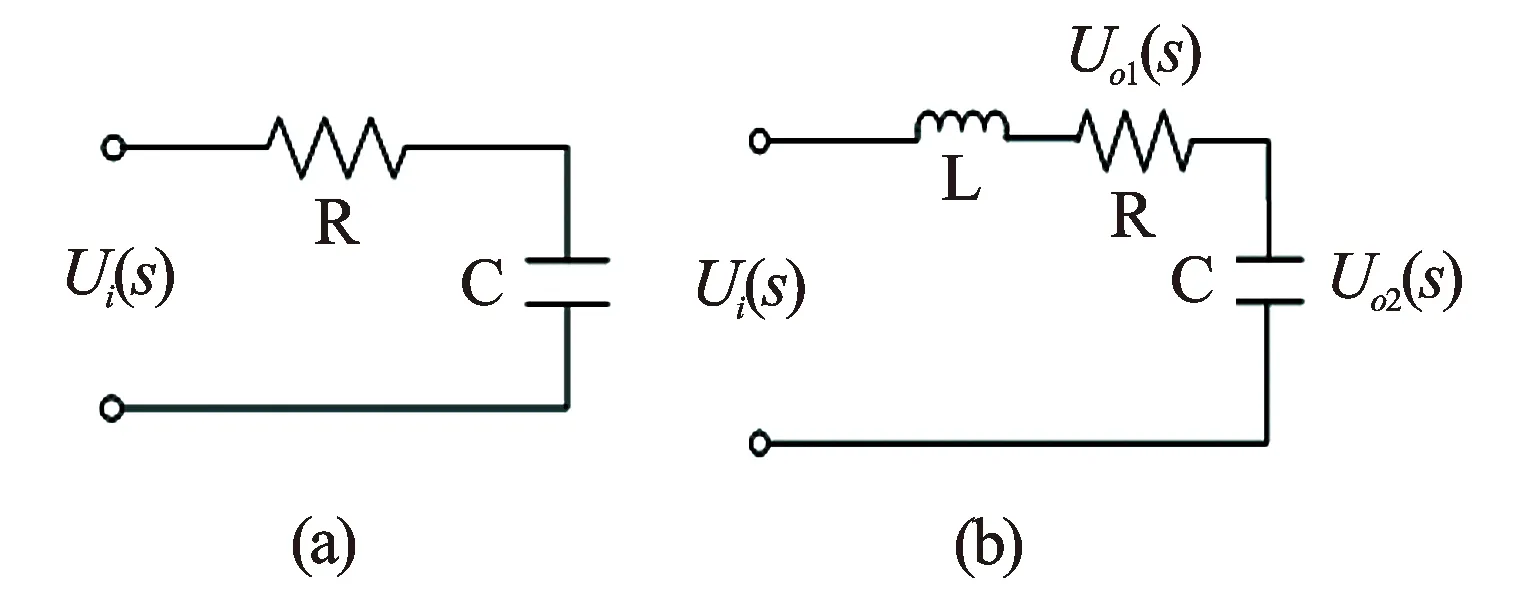
图3 一阶、二阶系统电路模型
图3(a)一阶电路模型的传递函数表示为
(9)
图3(b)二阶电路模型的传递函数表示为
(10)
(11)
对比式(9)、(10)、(11)与式(8)中各求和项的表达形式,可以发现只要选择合适的R、L、C参数值,便可找到式(8)中各项所对应的模型电路。除使用R、L、C这些无源器件外,设计中采用了运算放大器,不仅起到了隔离作用,避免了各级电路之间的相互影响,也便于实现信号的加减运算。从电路模型的建立过程可以看出,各模型中R、L、C的取值并非唯一,只要取值合理并能满足传递函数表达式即可。
设计经过求解、仿真,最终得到式(8)所对应的电路模型(见图4)。图5为图4电路的幅频特性的仿真结果与实测数据的对比图,其中‘*’表示所设计电路的幅度衰减特性,折线代表由实测数据预处理后形成的幅频特性曲线。从图5对比中发现,低频段电缆衰减特性时有起伏,电路模型的幅频特性与原数据存在个别偏离的现象;在较高频段,测井电缆本身衰减特性比较平滑,拟合效果非常好,整体可以满足设计需求。
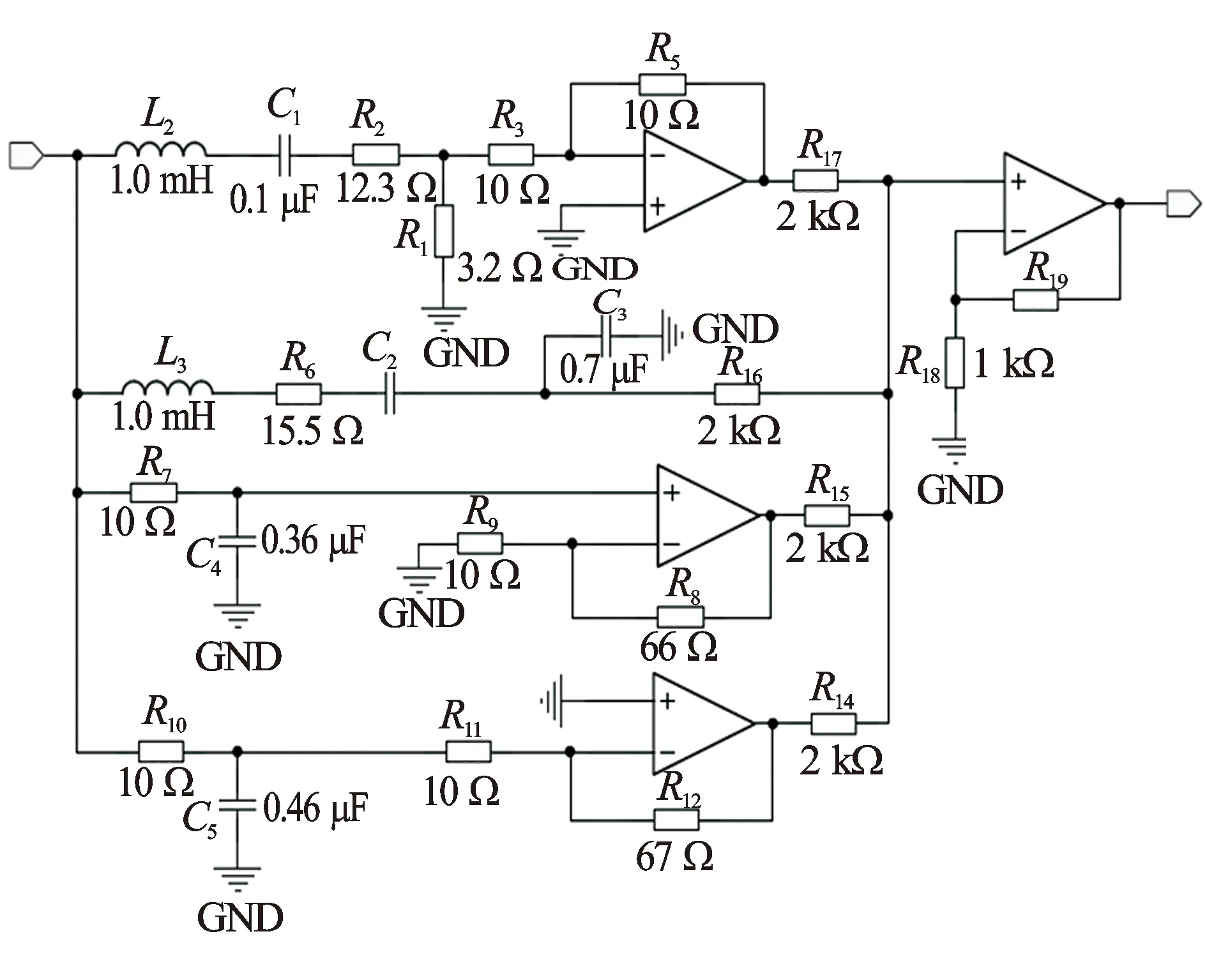
图4 式(9)对应的电路模型

图5 图(4)电路的幅频特性与原始数据对比
4 结 论
(1) 通过对测井电缆实施扫频测量所得的幅频特性离散数据进行分析,利用MATLAB自带的非线性最小二乘拟合函数找到与测井电缆衰减特性相近的系统传递函数,为其建立电路模型。
(2) 这种从测试到拟合再到设计的建模方法,可以使所建立的电路模型的幅频特性与实际电缆的特性非常接近,比通过采用测量设备直接对电缆参数进行测量的方法要准确很多。
(3) 设计中仅是在模式7特定连接方式下对测井电缆幅频特性的建模,并未考虑其相频特性。若要建立完整的符合七芯测井电缆频率特性的电路模型,需要对拟合算法、传递函数的阶数、参数初值的选取甚至电路的结构等做更全面、复杂的考虑。
参考文献:
[1] 董惠娟, 李瑞敏, 张广玉, 等. 单芯测井电缆频率特性分析 [J]. 光纤与电缆及其应用技术, 2008(6): 17-20.
[2] 郑君里, 应启珩, 杨为理. 信号与系统(上册) [M]. 2版. 北京: 高等教育出版社, 2000: 217-220.
[3] 胡寿松. 自动控制原理 [M]. 北京: 科学出版社, 2013: 179-184.
[4] 郑阿奇, 曹戈. MATLAB实用教程 [M]. 3版. 北京: 电子工业出版社, 2012: 1-3.
[5] 白涛. 用计算机实现频率特性到传递函数的识别 [J]. 中国高新技术企业, 2008(8): 114.
[6] 唐家德. 基于MATLAB的非线性曲线拟合 [J]. 计算机与现代化, 2008, (6): 15-19.
[7] 杨小锋. 测井电缆特性测试技术研究 [D]. 大庆: 东北石油大学, 2014.
[8] YANG J, ZHOU Q, QU C W, et al. Fast Estimation of Multilook K-distribution Parameters via the Least-squares Nonlinear Curve-fitting [C]∥Proceedings of 2012 IEEE 11th International Conference on Signal Processing, ICSP 2012.
[9] XU A Q, TANG X F, YANG Z Y. Mutant Generation for Analog Circuit Designs [C]∥Proceedings of 2014 IEEE 5th International Conference on Software Engineering and Service Science 2014.
