基于一种改进阈值函数的小波去噪方法研究

张金武，冯 毅，李 文

（华南理工大学 化工机械与安全工程研究所，广东 广州510640）

基于一种改进阈值函数的小波去噪方法研究

张金武，冯 毅，李 文

（华南理工大学 化工机械与安全工程研究所，广东 广州510640）

针对传统的阈值函数方法和阈值选取方法存在的一些不足，在现有的研究成果基础上，本文采用了一种改进的阈值函数方法，既克服了硬阈值函数的缺点，又减小了软阈值函数的偏差。通过MATLAB仿真，得出用本文方法去噪后的信噪比均在37.326以上，高于硬阈值函数的37.164和软阈值函数的37.265；均方差均在5.680以下，低于硬阈值函数的5.787和软阈值函数的5.720，说明本文改进的阈值函数方法去噪效果优于软、硬阈值函数，适用于含噪信号的分析和处理。

小波阈值去噪；MATLAB仿真；信噪比；均方误差

声音信号和图像信号的输入、采集、处理的每一个环节以及输出结果的全过程都不可避免的受到噪声的影响[1]。噪声一般都是随机信号，是不可预测的，如何剔除声音信号中的噪声，一直是信号处理过程中的重要研究内容。一般的去噪方法有线性滤波和非线性滤波，即把原始数据对应通过算术运算和逻辑运算得到滤波结果，这两种方法都会使得变换后的熵增高，而且信号的相关性也难以得到[2]。小波变换的低熵性、多分辨特性、去相关性使其在信号去噪方面占据了很大的优势，它的成果在语声人工合成、天体识别以及机器视觉等众多领域应用广泛。

在众多的小波去噪方法中，Donoho提出的阈值方法[3]最常用，该方法计算量小，实现简单，但也存在一定的缺陷。硬阈值方法对较大的小波系数不进行处理，将较小的小波系数置零，这就造成了门限阈值处的不连续，在重构信号时容易产生震荡[4]；而软阈值方法是把较大的小波系数均减去一个常数，导致重构信号时产生较大的均方差[5-7]。基于此，文中提出了一种改进的阈值函数方法，既克服了硬阈函数的缺点，又减小了软阈值函数的偏差。

1 小波阈值声音去噪方法

一个含噪声的一维信号模型可以表示为 f（t）=s（t）+σe（t），其中s（t）是原始信号，f（t）是含噪声信号，e（t）为噪声。由于小波变换是线性变换，所以对f（t）进行小波变换后，得到的小波系数分别对应着原始信号和噪声信号。因此就可以利用相应的数学工具构造某种特定的系数选择方式，最大限度的把由噪声变换所得的小波系数剔除，把原始信号变换所得小波系数保留下来，再进行信号重构得到去噪后的信号。所以，去噪的关键步骤之一就是对小波系数的量化处理。常用的方法有基于模极大值去噪法，平移不变量法，阈值法。

1.1 小波阈值去噪原理

一般情况下，含噪信号经过小波分解后，噪声的系数通常要比信号的系数小。因此就可以选定一个合适的数λ作为阈值，若小波系数大于这个值，就认为这个系数是由信号引起的，系数则保留下来；若小波系数小于这个值，便认为这个系数是由噪声引起的，剔除这部分系数[8-10]。因此，信号的降噪过程可以按照下列方法进行：首先对含有噪声的信号S进行小波分解，三层分解过程如图1所示，则分解噪声所得到的小波系数通常在CD1、CD2、CD3。这样一来，就可以设定一个门限值，对这些小波系数进行处理，再进行小波逆变换重构过程，就可以达到降噪的目的。

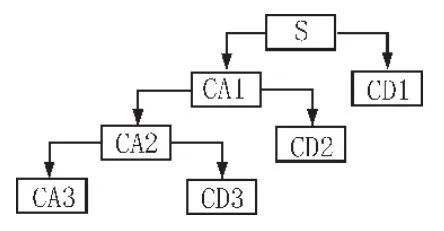
图1 三层小波分解示意图

综上，小波阈值去噪大致可以分为以下3个步骤[11]：1）小波分解：分解含噪信号得到各层的小波系数；2）阈值量化：对每一层的高频小波系数进行处理，得到估计的小波系数；

3）信号重构：根据低频小波系数和估计的高频小波系数，进行一维信号小波重构。

为了得到更好的降噪效果，选取合适小波和分解层数，合适的阈值和量化方法是至关重要的，往往需要通过大量的仿真实验来对这些方法进行实验并进一步改进，来使得去噪方法具有较好的通用性。

1.2 小波阈值函数的选取

1.2.1 硬阈值函数和软阈值函数

阈值函数的选取在重构信号的过程是起着至关重要的作用，Donoho提出了如下两种阈值函数，这两种阈值函数去噪法在工程中得到了广泛的应用。

其中sign（n）为符号函数，其表达式如下：

式中λ为门限阈值，ωj，k为原始信号经小波变换后所得的小波系数，ωˆj，k为估计的小波系数。两种阈值函数的示意图如下，从图中我们可以看出，硬阈值函数在门限阈值处是不连续的，这将使得重构信号产生震荡；软阈值函数虽然连续，但经过处理的小波系数与原信号小波系数存在固定的偏差，重构之后声音信号可能会产生一定程度的失真。

图2 软、硬阈值函数示意图

1.2.2 改进的小波阈值函数

为了获得更好的去噪效果，诸多学者对阈值函数提出了改进，有学者提出了一种软硬阈值折衷函数，对上文的量化方法定义作稍微的修改，引入新的定义如下：

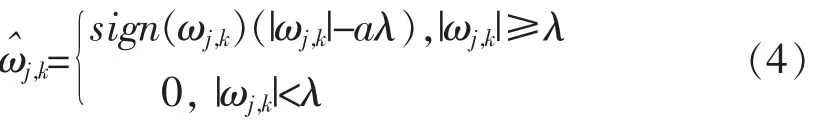
式中，0≤a≤1，当a取0时，上式便成为硬阈值方法；取1时成为软阈值方法。虽然该方法对软硬阈值函数进行了折衷 ，但其却同时具备了软硬阈值法的缺点。基于相关文献中改进阈值函数的思想[12]，本文对折衷法进行了改进，改进的阈值函数如下：

式中，0≤a≤0.1，a的取值上限做适度微调，可能会取得更好的去噪效果，当a=0时，该式即为软阈值函数。由小波变换去噪的知识可知，较小的小波系数也是由有用信号和噪声信号构成的，只是有用信号对较小的小波系数贡献小，上述几种阈值方法中均将较小的小波系数直接置零，这都使得有用信号产生了一定的损失。文中，将较小的小波系数乘以一个较小的常数，这就保留了小波系数中对应的部分有用信号，对于较大的小波系数，处理方法与软阈值函数类似，但并不是直接减去门限阈值。该方法既有连续性，又一定程度上降低了重构信号时产生的均方差，具有较好的降噪效果。其函数图像如图3所示。

图3 改进阈值函数示意图

1.3 阈值的选取

阈值的估计也是去噪过程当中的一个重要环节，阈值选取过大，则在量化过程中较多有用信号将被舍弃；阈值选取过小，则去噪不够彻底。通常有4种可供选择的估计方法[13]：

2）自适应阈值：自适应阈值是基于阈值必须能随着小波系数的变化而改变的思想提出来的。自适应阈值取为，其中t为给定阈值的似然估计。

3）启发式阈值：采用固定和自适应阈值方法的结合。设M为小波分解某一层所有的N个小波系数的平方和，令m=（M-N）/N，n=（log2N）1.5，则混合阈值λb为：

4）极大极小阈值：该方法采用的也是一种固定的阈值。

在实际工程应用中，往往对固定阈值进行适度改进，有学者以尺度的不同选取每一分解层的固定阈值λj，取，本文将在该方法基础上进行进一步改进。

2 基于MATLAB的实验仿真

2.1 去噪效果评价指标

为了比较不同阈值降噪方法的降噪效果，此处引入如下两种评价指标。

1）信噪比[14]：信噪比常用来作为去噪效果的判断依据。国际上信噪比的单位是分贝（dB），信噪比通常定义为:SNR=10log

2）均方误差[15]：

2.2 实验仿真

文中的仿真实验对象是leleccum信号，采样点数为1 024，并加入高斯白噪声形成待处理的信号，用 db3小波进行 5层分解处理，阈值取 λj=，符合噪声对应的高频小波系数随着分解层次的增大而减小的规律，其中dj为第j层高频小波系数。在此说明，这里的阈值选取并不是最优的，如果阈值选取恰当，则更能体现出本文所提方法的优越性。对该信号分别进行软、硬阈值和改进阈值方法去噪实验，实验中参数a的值分别选0.01，0.04，0.07，0.10，实验结果如图4图5所示。

通过仿真图可以看出，用改进的阈值函数处理信号后进行小波重构比其他两种方法更加接近原信号，因而能更好地还原原始信号所包含的信息。为了更加精确评价去噪效果，分别计算上述方法的信噪比和均方误差，计算结果如表1所示。

3 结 论

文中首先对小波阈值去噪的基本原理进行了分析，并进一步阐述了其一般步骤，然后在介绍阈值函数和阈值选取的基本类型的基础上，综合分析了硬阈值和软阈值函数方法的不足，采用了一种新的阈值取法，并提出了阈值函数改进方法，该方法继承了软阈值函数连续性的优点，能更加真实地还原原信号。

最后通过MATLAB仿真实验，对比去噪效果图和评价指标（SNR、MSE）可知，相比传统阈值函数，本文提出的新阈值函数得到的信噪比更大，均方误差更小，因此具有更好的去噪效果。

[1]蒋薇薇，鲁昌华，张玉钧，等.基于提升小波改进阈值的光谱信号去噪研究[J].电子测量与仪器学报，2014，28（12）:1363-1367.

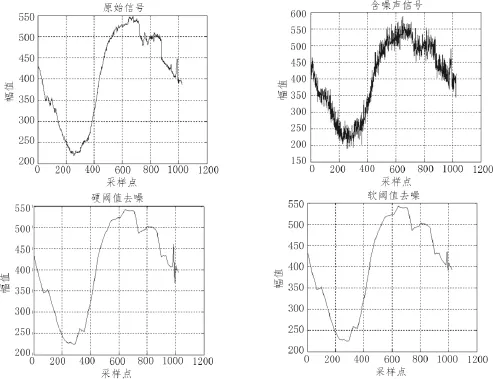
图4 软、硬阈值函数去噪效果图

图5 改进阈值函数去噪效果图

表1 3种阈值函数的去噪效果比较

[2]杨红强，米根锁，王宝宝.自适应小波阈值算法在应答器信号去噪中的应用 [J].河南科技大学学报：自然科学版，2016，37（1）:31-34.

[3]姚宗娜，魏延鑫.基于新阈值函数的小波阈值自适应去噪[J].信息技术，2014（11）:12-15.

[4]刘梦姣.基于小波阈值去噪法阈值函数的研究[J].装备制造技术，2016（2）:227-228.

[5]邵鸿翔，高宏峰.改进小波阈值去噪方法处理FBG传感信号[J].激光与红外，2014，44（1）:73-76.

[6]张建国，王文博.一种改进的经验模态分解消噪阈值函数[J].中国科技论文，2013，8（10）:1064-1067.

[7]吴光文，王昌明，包建东，等.基于自适应阈值函数的小波阈值去噪方法[J].电子与信息学报，2014，36（6）:1340-1347.

[8]王宏强，尚春阳，高瑞鹏，等.基于小波系数变换的小波阈值去噪算法改进[J].振动与冲击，2011，30（10）:165-168.

[9]何婷，常勇.小波阈值启发的EMD降噪新方法[J].自动化与仪器仪表，2014（11）:70-75.

[10]向东阳，吴正国，侯新国，等.改进的多小波变换系数相关去噪算法[J].高压电技术，2011，37（7）: 1728-1733.

[11]朱俊，高静.基于小波分析的线性调频信号降噪研究[J].电子设计工程，2014，22（7）:117-119.

[12]王蓓，张根耀，李智，等.基于新阈值函数的小波阈值去噪算法[J].计算机应用，2014，34（5）:1499-1502.

[13]司祯祯.傅里叶变换与小波变换在信号去噪中的应用[J].电子设计工程，2011（4）:155-157.

[14]章浙涛，朱建军，匡翠林，等.小波包多阈值去噪法及其在形变分析中的应用 [J].测绘学报，2014，43（1）:13-20.

[15]孙海亮，訾艳阳，何正嘉.多小波自适应分块阈值降噪及其在轧机齿轮故障诊断中的应用[J].振动工程学报，2013，26（1）:127-134.

Research on wavelet denoising method based on an improved threshold function

ZHANG Jin-wu，FENG Yi，LI Wen
（Institute of Chemical Machinery and Safety Engineering，South China University of Technology，Guangzhou 510640，China）

In view of the disadvantages of the traditional threshold function method and the threshold selection method，this paper proposes an improved threshold function method based onexisting research results，which not only overcomes the shortcomings of the hard threshold function，but also reduces the deviation of the soft threshold function.By conducting MATLAB simulation experiment，we conclude that the SNR of the method used in this paper is more than 37.326，which is higher than 37.164 ofthe hard threshold function and 37.265 of the soft threshold function；the MSE is below 5.680，which is less than 5.787 of the hard threshold function and 5.720 of the soft threshold function，the result shows that denoising effect of the improved threshold function is better than the traditional methods，and it is suitable for the noisy signal analysis and processing.

wavelet threshold denosing；MATLAB simulation；SNR；MSE

TN912.3

A

1674-6236（2017）09-0137-04

2016-05-30稿件编号：201605280

张金武（1990—），男，江西南昌人，硕士研究生。研究方向：机械设备的故障诊断。