基于小波分析的弱信号检测及其电子测量系统应用

乔彦超

（河南省科学院 应用物理研究所有限公司，河南 郑州450008）

基于小波分析的弱信号检测及其电子测量系统应用

乔彦超

（河南省科学院 应用物理研究所有限公司，河南 郑州450008）

对于信号测量系统，从复杂环境中提取出弱信号一直是研究的重点。文中针对从强噪声中提取微弱信号的问题，在利用小波分析法进行数据处理分析的基础上，通过研究信号和噪声在小波变换后的情况，并根据频谱的相关信息，提出新的阈值处理算法。仿真实验证明了所提算法的正确性和有效性。在此基础上搭建了一个电子测量系统进行相关的信号处理，并利用该系统验证了新算法的性能。

小波分析；信号测量；电子测量系统

在信息高度密集的社会中，诸多信号均依靠数据测量才能准确收集。但若在被测信号极其微弱的情况下，易被噪声干扰到，这就大幅增加了信号检测的难度。弱信号检测（WSD）就是通过电子学原理和信号分析技术，从噪声之中消除混杂信息得到有效信号。在强噪声情况下，现行的检测方法无法满足对信号精确度的要求。所以，亟需寻找到弱信号检测新的突破点[1]。

文中主要是研究在弱信号检测过程中如何运用小波分析理论进行处理，根据噪声的能量分布特点，利用小波变换进行算法处理，达到从有色噪声信号中获得所需的微弱信号。这种新算法可大幅度的提升对微弱信号的还原度，鲁棒性优良，并可较好地应用在噪声污染较大场合的信号分析工作之中。同时，本文使用虚拟仪器技术设计了一个多方面联动的电子测量系统，从实际验证了小波分析算法的理论[2]。

1 原理及仿真

1.1 小波分析的原理

小波变换满足了非平稳信号最为关键的时频上的特性，其可将信号中的能量聚集到部分的小波系数上。可使用小波变换对信号进行处理，并解析出其中的尖峰和突变部分[3]。

一个含噪信号为：y=x+εn。信号处理即是从被污染的信号y中，找到真实信号x，抑制或消弭噪声εn。假使令xˆ为已过滤的信号，t是初设阈值，X、Y是x及y的小波变换，其中X是Y对X的估计。一维信号去噪通常可经过下面3个步骤[4]。

步骤1确定一个需要进行分析的目标小波，对其开始N层小波分解；

步骤2使用阈值方法对上一步处理后出现的高频系数进一步分析；

步骤3根据每一层的高频系数情况分配对应的阈值，常用的有两种：

软阈值方法

硬阈值方法

根据第N层的低频系数，阈值处理后的每一层高频系数，对信号加以小波重构。

每一层对应特定的阈值，比较小波变换系数与阈值。若此阈值比系数大，则认定为属于噪声的，按零值处理。若阈值小于系数，就保持不变，达成去噪的效果。常规的认定选定阈值为信号的长度N和噪声方差ε的函数t（N，ε）。

小波消噪的过程中，一般的阈值量化方式有：强制消噪、固定阈值消噪、给定软（或硬）阈值消噪[5]。

阈值选择规则是基于基本模型s（i）=f（i）+σe（i）。式中e（i）为白噪声N（0，1）。可选择以下几种阈值：

1）根据史坦的无偏似然估计原理进行阈值选择。

3）最优预测变量阈值选择。

1.2 算法设计

运用信号小波分析的方法对噪声进行研究。根据一般理论，对于一个一维的信号高频部分主要干涉小波分解的第一层，而低频层则受低频部分影响较大[6]。

1.2.1 频谱分析

建立一个有色噪声的数学模型，回归公式为

其中，b1（t）是白噪。该信号是一个非白噪声，其的频谱几乎只在高频段（见图1）。即信号的多数能量是存在d1上的。

1.2.2 基于频谱分析的小波算法设计

根据上文小波变换的消噪步骤，参考常规消噪方法，对该方法进行改良：

图1 含有色噪声信号经5层db3小波分解后的各层分量

1）强制消噪处理。将较低层高频系数全部变为0。

2）默认阑值消噪处理。用默认阈值处理较低层的高频系数。

3）固定软（或硬）阈值消噪处理。以固定软（或硬）阈值处理较低层的高频系数。

这种方法主要是进行信号噪声的频谱分析，并根据对频谱特性的解析，最终达到信号噪声的消噪处理。

1.2.3 算法仿真

含有色噪声信号，如图2（a）所示。进行db3分解，使用不同的阈值算法进行分解，效果亦不相同。表1呈现了几种消噪效果的误差分析，从下面三图及误差分析表可得出结论，图2（b）软阈值处理可较好地消噪，但在含噪信号比较混乱时，较为平滑。图2（c）硬阈值消噪结果并不理想，信号中的噪声并未滤除。图2（d）是改进算法（将低层高频系数dl进行阈值处理）处理的结果，可看出相比其他的处理方法效果更令人满意。从误差分析中也可证明这一点[7]。

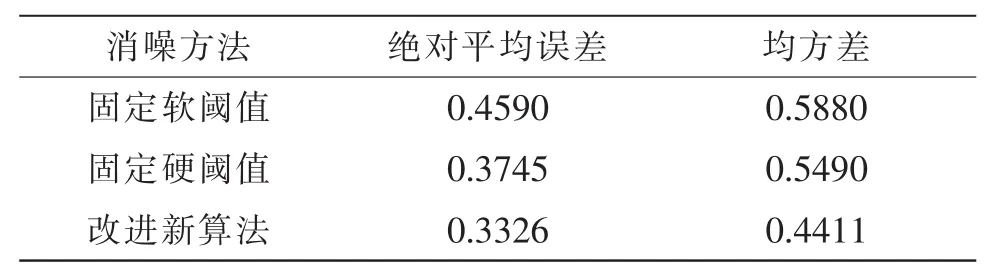
表1 误差分析

有色噪声的能量聚集在小波变化的低层高频dl，在dl层运用特定的阈值进行优化，按时间条件对分解信号进行分析，分段计算得到新的阈值，最终达到符合条件的消噪效果。

在分析含有色噪声的情形中，这种改良的算法可大幅度提高误差的精度，在此基础上也延续了原方法的基本理论和优点，对算法进行精简处理。其不仅能去除噪声，更能使算法具有计算效率，在应用时可较为快捷和准确的获得目标信号[8]。

图2 算法仿真结果

2 在电子测量系统的主要应用

在当前时兴的电子测量新技术中，小波分析更受研究者青睐。运用小波分析进行信号处理，能够分解信号的低频和高频，即信号的近似部分和细节部分。在此基础上，可发现信号的间断点，后续情况有利于故障预警。为了适应研究人员对电子测试系统的新需求[9]，文中设计了一个电子测量系统，在该系统中，可验证小波分析在信号检测中的正确性并值得加以应用。

本系统是综合了虚拟仪器技术的，集合了多种电子测量的功能。将相关仪器的参数和精度联合设计在一个电子测量系统上，并利用有着特定功能的软硬件布置，实现测析一体化电子测量系统。

2.1 硬件结构

电子测量系统的配置位宽为200的测量总线，对于其他结构有失真度分析仪、4信道数字存储示波器、136信道逻辑分析仪、扫频信号发生器、136信道数字信号发生器和48信道模拟信号FO端口等仪器模块[10]。

事件处理机是整个系统的核心部分，主要任务是控制设备与主机的数据交换，分析随机事件信号，根据设定保证硬件模块的工作。文中用FPGA实现了该事件处理机，大小为16*16*16。

图3 硬件结构框图

2.2 软件设计

2.2.1 软件架构

电子测量系统软件是在WindowS的基础上进行设计的，包括系统总控管理层、功能模块层、设备管理层。其最高层是总控管理模块，这个部分是各种仪器模块的组合设计，主要是电子仪器的组合方式和显示格局。

功能模块层聚集了各类仪器的功能，负责各类数据的测量。仪器模块还有着 “输入”和“输出”之分。设备管理层联系着系统程序与硬件的命令传递，主要任务是根据应用程序的请求对设备进行映像。其中，驱动程序设计是核心部分，驱动函数有连接、参数读写和运行启动等。

选用LabWindows/CVIS.0作为系统模块的实施工具。举例对利用CVI的模块开发做出说明。第一步需要一个信号发生器的USER接口，再者此站点可产生电压、电流两个种信号。所以，必须要有电压源与电流源信号设置的两个数据设置表，另外的功能有波形呈现界面、调整波形显示的分度调节控件等。信号发生器可产生多种信号，如能正弦波、调频、扫频、方波、阶梯波以及噪声等[11-13]。

2.2.2 基于LabWindows/CVI的软件模块设计

系统是在Windows环境下进行设计的，程序环境是LabWindows/CVIS.0。对于在软件层次上，需要对通信模块和设备控制过程进行详细设计[14]。

1）通信模块设计是为了实现软件对硬件的控制，主要部分如下：

CVI控件：该控件负责软件与用户操作信息的流通，利用CVI CallBack过程与指令发生器传递数据要求。

CVI回调过程：CVI Callback是CVI控件与软件的联系点。Cmd Creator（指令发生器）负责分析接口CVI Control传递的信息，并根据设计表格发出硬件的动作指令给Cmd Event Queue。

队列指令：Cmd Event Queue是程序传递中的内存，负责与设备的通信息交换。

设备通信模块：Cmd Event Queue给予指令，控制硬件的逻辑动作，并将结果和数据传递给Data Event Queue。

数据分发过程：Data Event Queue将数据传递给Data Dispatcher，并对数据进行分类，按要求传递到CVI控件显示。

2）设备控制设计过程包括调整软件接口来控制硬件设备，一般情况有以下四种模块：指令发生、数据分发、定时激励和通信。

2.3 小波分析算法在系统中的应用

在Matlab的原有系统上，运用小波分析算法操作的功能代码如下：

第一步：打开matlab

调 用 函 数 ：MLApp_NewDIMLApp（NULL，&hMatlab）；

该函数在matlabsrvr.c中定义，意在新建一个matlab句柄。通常在新建句柄后会调用Min Max Matlab（）函数来定义matlab的窗口显示。

第二步：发送矩阵函数

调用函数：SendMatrix（hMatlab，”ewave”，（double*）wave，NULL，1，1024）；

该函数在 matlabutil.c中定义，意在说明向matlab发送数据。

第三步：运行matlab命令函数

调用函数：RunMatlabCommand（hMatlab，”小波函数命令”；

根据算法格式，在“小波函数命令”内添加小波matlab算法，再通过函数 GetMatrix（hMatlab，xd，&matrixReal，&matrixlinag，&dim1，&dim2）提取处理后的数据。

第四步：关闭matlab

调用函数：MLAPp_DIMLAppQuit（*hMatlabPtr，NULL）；

演示：在系统中，使用自带的信号发生器发出单频正弦信号，如图4所示。发出信号参数如下：50 mv的正弦电压信号，取垂直分度为50 mv/div，信号频率为10 kHz，水平分200 us/div。将输出信号通过信号传输线传递到示波器的CH1接口。为自动采样，取采样深度为8 K，采样频率100 MSa/s，如图5所示。因电压比较微弱，采集出的波形含噪过大。故先使用Lab-windows/Cvl内置的Butterworth滤波器程序，得到图6波形图。根据波形图，发现消噪后的信号干扰有所减少，但失真较为严重。再采用经过小波分析的算法，处理过后得到图7的波形图。从图中可看出，所得到的波形与原波形相差较小，能在混杂的信号中准确的解析出原始信号，并维持信号的完整性，由此证实了该种算法的可应用性。

图4 单频正弦信号

3 结束语

小波分析的时频局部性优良，对于信号而言，经过小波变换后可将信号解析成各个频率成分。这样对于信号滤波、分离噪波和弱信号的研究均有着重要作用。针对如何在复杂环境中排除干扰，从带噪声的信号中获得微弱的原始信号问题，本文通过改良算法并进行仿真验证，设计了一个电子测量系统，并根据系统的实验环境及MATLAB和Labwindows混合程序设计验证了小波变换[15]在信号分析中主要的具体应用，且电子测量系统能为小波理论的分析实践提供平台。

图5 原始信号

图6 Butterworth滤波器处理后的波形图

图7 小波算法处理后的波形图

[1]杨汉祥.微弱信号检测技术的研究[J].科技广场，2009（1）:27-30.

[2]范晓志，王长广，黄晓红，等.基于小波分析和多重自相关法的微弱信号检测技术[J].计算机应用与软件，2007，24（5）:40-41.

[3]王振宇.MCF51QE128的微弱信号检测技术研究[J].单片机与嵌入式系统应用，2014，14（1）:28-30.

[4]谢水珍.基于Labview的虚拟函数信号发生器的设计[J].微计算机信息，2007，14（1）:181-182.

[5]王慧，胡仁杰，康凯.基于虚拟仪器技术的电气测试平台的实现[J].计算机技术与发展，2008，18（5）: 194-196.

[6]S.Zhang，E.Salari.Image denoising using a neural network based non-linear filterin wavelet domain [J].IEEE Trans.on Sp，2005.

[7]侯国屏，王坤，叶齐鑫.LabVIEW7.1程序设计与虚拟仪器设计[M].北京:清华大学出版社，2005.

[8]葛哲学.小波分析理论与MATLAB R2007实现[M].北京:电子工业出版社，2007.

[9]陶珂.小波去噪质量评价方法研究[D].长沙:中南大学，2012.

[10]蒋蕾.基于小波理论的电能质量信号去噪方法的研究[D].锦州:辽宁工业大学，2015.

[11]张晓宁，孙丽君.一种改进的小波阈值信号去噪方法[J].电子科技，2012，25（11）:15-17.

[12]王拴中，朱玉田.改进小波阈值去噪法的对比性仿真实验与分析[J].噪声与振动控制，2012，32（1）: 128-132.

[13]周帅，左东广.基于改进阈值函数和自适应阈值的小波去噪方法[J].电子科技，2012，25（11）:31-34.

[14]梁跃.基于小波包变换的地电场信号去噪研究[D].哈尔滨:东北农业大学，2014.

[15]刘凤魁，邓春宇，王新迎.基于小波变换和改进快速密度峰值聚类算法的负荷曲线聚类研究[J].电力信息与通信技术，2017（3）：55-61.

Weak signal detection based on wavelet analysis and its application in electronic measurement system

QIAO Yan-chao
（Henan Academy of Sciences Institute of Applied Physics Co.，Ltd.，Zhengzhou 450008，China）

For the signal measurement system，to extract a weak signal from a complex environment it has been the focus of the study.The paper for the extraction of weak signal from strong noise problems in the data processing and analysis using wavelet analysis method，based on the research of signal and noise in the case of wavelet transform and the spectral information，propose new thresholding algorithm. The simulation results show the correctness and effectiveness of the proposed algorithm.On this basis，to build an electronic measurement system associated signal processing，and use the system to verify the performance of the new algorithm.

Wavelet analysis；signal measurement；electronic measuring system

TN99

A

1674-6236（2017）09-0054-05

2016-06-24稿件编号：201606190

乔彦超（1967—），男，河南新郑人，高级工程师。研究方向：电子技术应用。