隧道下穿高压管道沉降控制标准分析

张运涛(中铁第一勘察设计院集团有限公司，陕西 西安 710043)

隧道下穿高压管道沉降控制标准分析

张运涛
(中铁第一勘察设计院集团有限公司，陕西 西安 710043)

伴随地铁隧道和高压燃气管道的加速建设，新建地铁隧道工程下穿高压燃气管道的案例也逐渐增多。而我国相关规范只给出了有关高压管道的曲率半径的控制指标，实际工程常以沉降变形作为高压管道的控制指标，而且绝大多数的控制标准缺乏理论依据。本文依据规范规定的弹性敷设管道的曲率半径计算公式以及修正的沉降槽宽度计算公式，从理论上推导出高压管道沉降控制标准计算公式，结合模型分析和实测结果，验证了理论分析结果的可靠性。

隧道；高压管道；曲率半径；沉降槽宽度；沉降标准

地铁建设中难免遇到各种不同的管线，特别是压力管线，一旦发生险情，其危害难以控制。近年来，随着国内各大城市地铁建设的蓬勃发展以及天然气管道的加速建设，必将出现地下工程下穿高压燃气管道的建设问题。以厦门为例，自2008年以来，厦门市现已建成两座天然气接收门站、6座高中压调压站，敷设高压输气主干管38 km、中压管网700 km。同时，至2020年厦门城市轨道交通项目已规划了6条线路，总计里程232 km。

目前，国家和地方相关规范对地下工程下穿管道的要求尚有不足，多数管道设计规范只明确了对管道曲率半径的要求。如文献[1]只规定了弹性敷设管道的曲率半径应满足其强度的要求，且不应小于钢管外径的1 000倍，垂直面上弹性敷设管道的曲率半径还应大于在自重作用下产生的挠度曲线的曲率半径。文献[2]对于水平定向钻法穿越设计采用弹性敷设时，穿越管段曲率半径不应小于1 500钢管外径，且不应小于1 200倍钢管外径。多数地方性城市轨道交通规范依据工程经验规定了隧道下穿管道的一般性沉降控制标准，一些文献也对此进行了探讨。如文献[3]结合以往盾构区间隧道下穿管道控制标准制定的经验值，并根据管道的特性及其所处的工程地质条件，得出了将30 mm作为管线下方土体失效后管线沉降的控制标准。除此之外，一些工程实例结合工程经验和规范对管线沉降控制标准做出了规定，但在实际工程中这些标准过于保守，如深圳地铁5号线，在监测过程中大多数管线的沉降都超过了35 mm的控制值，但管线还是安全的[4]。

通过分析规范要求，结合一定的理论计算，对隧道施工下穿高压管道的沉降控制标准进行理论推导，得出理论允许沉降量。

1 高压管道曲率半径计算原理

高压钢管管道在弹性敷设条件下具有一定的弯曲变形能力，且管道间均为焊接连接，因此管道具备一定的轴向弹性变形能力，管道的沉降控制标准值可通过管道的轴向允许曲率半径的大小确定。在弹性敷设假定条件下，管道周边土体发生不均匀沉降而造成的钢管轴向弯曲变形，主要体现在管道的竖向曲率半径上[5]，规范中明确给出了两种关于高压钢管管道的竖向曲率半径的取值方法：

(1)根据《输气管道工程设计规范》(GB 50251-2015)确定曲率半径。

弹性敷设管道的曲率半径除应满足其强度要求外，还不应小于钢管外径的1 000倍，垂直面上弹性敷设管道的曲率半径还应大于管在自重作用下产生的挠度曲率半径，曲率半径计算公式为：

(1)

式中：R为弹性弯曲曲率半径，m；a为管道的转角，(°)；D为钢管外径，cm。

根据规范的定义，管道在自重作用下产生的竖向挠曲率半径可以由(1)式确定，管道转角可解释为在弹性敷设条件下，管道由于自重作用发生轴向弯曲产生的管道转角变形。一般情况下，管道在实际工程中由于自重产生的转角a相对较小，公式(1)可以简化为：

(2)

式中：符号同前。

(2)根据《油气输送管道穿越工程设计规范》(GB 50423-2013)确定曲率半径[2]。

对于水平定向钻法穿越设计采用弹性敷设时，穿越段管道的曲率半径不应小于1 500钢管外径，且不应小于1 200倍钢管外径，即：

R≥1500D

(3)

(3)考虑到工程的实际需要以及高压、超高压天然气管道对长期运营安全的需要，建议在役高压及超高压弹性敷设的管道，沉降后的曲率半径应满足：

(4)

2 沉降槽宽度的确定

为分析隧道下穿高压管道的沉降控制标准，在明确钢管管道的最小曲率半径的基础上，还需要确定管道在弹性敷设条件下，周边土体发生不均匀沉降的横向宽度，即沉降槽宽度。

2.1 定义

当采用暗挖法进行土体开挖时，会不可避免地造成地层移动，从而造成地表发生沉降，这种沉降在水平方向上的延伸长度称为沉降槽宽度。一般情况下，对环境和各类建(构)筑物造成不利影响的距离称为沉降槽宽度[6-7]。目前具有代表性的沉降槽宽度计算方法有两种：

(1)R.B.PECK公式，目前由于地层开挖所引起的沉降计算常采用Peck公式进行计算预测，Peck提出土体开挖后正上方地表沉降槽的形态可用正态分布函数来表述[8]，即：

(5)

式中：x为距隧道中线的距离；S为距隧道中线为x的地表沉降量；Smax为隧道中线处的最大沉降量；i为沉降槽宽度系数。

(2)随机介质理论法：根据随机介质理论的定义，针对某开挖单元，在不排水、不固结、密度不变的条件下，隧道开挖引起上部土层某点(x,y,z)处的沉降量为[9]：

(6)

式中：r(z)为微单元开挖在深度为z的水平面上的主要影响半径，或称为主要影响范围，即沉降槽宽度。

文献[6-7]总结并分析了Peck公式和随机介质理论之间的对应关系，Peck公式是随机介质理论方法的一种近似。两者与沉降槽宽度有关的系数(即随机介质理论中的主要影响半径和Peck公式中的参数i)之间有如下关系：

(7)

2.2 沉降槽宽度系数

(8)

式中：i为沉降槽宽度系数；z0为隧道中心处的埋深；φ为隧道拱顶上部土体各土层内摩擦角的加权平均值。

3 高压管道理论沉降分析

目前对于高压管道及超高压钢管管道的理论允许沉降值分析常采用两种理论确定：一种是基于圆曲线沉降槽分布曲线进行求解；二是基于PECK 沉降槽理论进行分析。

3.1 基于圆曲线沉降槽理论进行管道沉降分析

文献[3]、[5]、[11]给出了圆曲线沉降槽分布理论的分析成果，根据文献中的假定，隧道下穿管线引起的管线沉降曲线如图1所示，管道未发生沉降下为直线状态，当采用暗挖进行管线下部土体开挖时，管道由先前的直线状态转变为圆曲线分布状态，这里整条圆曲线具有相同大小的曲率半径，其中，F和F’为圆曲线的反弯点。

根据管线沉降示意图1中的几何关系可以得出管道沉降量的基本关系式：

h=R(1-cosβ)

(9)

Smax=2h

(10)

式中：β为管道周边土层发生不均匀沉降导致管道发生的转角；Smax为管道最大沉降值。

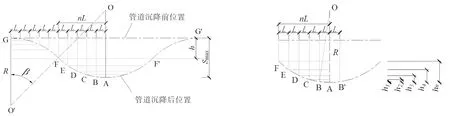
图1 管道沉降曲线示意图 图2 管道沉降量示意图

根据图2管道沉降量示意图，将弧FA对应的直线段管道等分成n份，每段长度为L，则根据勾股定理可以得出：

(11)

其中，kh≪R，因此可以近似得到：

hn=(nL)2/2R

(12)

公式(12)的结果表明：沉降曲线上各点的理论沉降量与曲率半径R成反比，与各点距离隧道中心的水平距离成反比。

根据圆曲线沉降分布的分析结果，在役高压燃气管道的理论允许沉降量需根据管道曲率半径和沉降槽宽度共同确定，假定圆曲线分布状态下的沉降槽宽度与PECK 理论下沉降槽宽度相等，因此可以求得管道沉降最大控制值：

Smax=(1.25i)2/R

(13)

3.2 基于 PECK 公式进行管道沉降分析

PECK提出了地表沉降分布形态为正态分布曲线，即公式(5)给出表达形式，可以看出在正态分布假定下，沉降槽各点处的曲率半径是不同的。为分析在基于沉降变形曲线为正态分布函数下各点处的最小曲率半径，可以对公式(5)求导并根据曲线某点处的曲率半径公式得到：

(14)

(15)

将公式(3)确定的管道最小曲率半径带入公式，即可得到最大理论沉降值为：

(16)

3.3 结果对比

两种不同假定下的分析结果表明：管道理论最大沉降量与两个因素有关，一是沉降槽宽度系数，二是管道的曲率半径的大小。管道最大的理论沉降量与管道的曲率半径成反比，与沉降槽宽度系数的平方成正比。相比之下，管道在圆曲线理论假定下其最大理论沉降量要比PECK 公式假定下的解大56%，即表明由PECK公式得到的管道沉降控制标准值更为严格。对于高压及超高压管道应采用公式(16)确定管道沉降控制标准。

4 工程实例

4.1 工程概况

某市地铁区间下穿高压LNG燃气管线，管线埋深4.78～5.16 m，区间隧道顶部距离LNG管线中心距离约为11.7 m。区间隧道下穿段的土层主要为素填土、粉质黏土、残积砾质黏性土、全风化花岗岩、散体状强风化花岗岩和碎裂状强风化花岗岩。隧道下穿LNG管线段见图3。

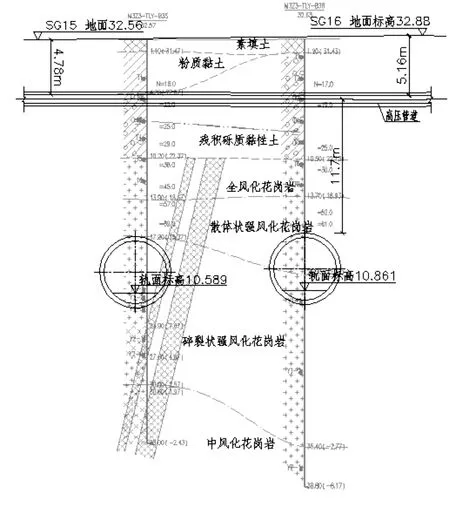
图3 隧道下穿高压管道横剖面图(单位：m)

4.2 管道理论沉降量分析

采用公式(8)对本盾构区间地表沉降槽宽度进行了预测，隧道半径为3.1 m，结构顶部距离管道中心为11.6 m，根据表1中所给地层参数计算得到隧道上部土体加权平均摩擦角为24.6°，分析得出单线隧道施工完成后其沉降槽宽度为19 m，管道发生轴向弯曲的最小曲率半径为R=1 066.5 m。

根据公式(8)可求解得到沉降槽宽度系数i=3.8 m。

在PECK分布假定下，由公式(16)可以得出最大理论沉降量为13.5 mm；而根据圆曲线分布假定下，得到管道最大理论沉降量为21.2 mm。

根据对LNG燃气管道的重要程度判别为重要管道，发生风险等级较高，管道周边地质条件主要为黏土以及强风化花岗岩；同时结合管道产权单位的要求，综合分析后得出对高压燃气LNG管道，单线隧道开挖后管道发生最大理论沉降量为13.5 mm，以此作为高压LNG管道的沉降控制标准。

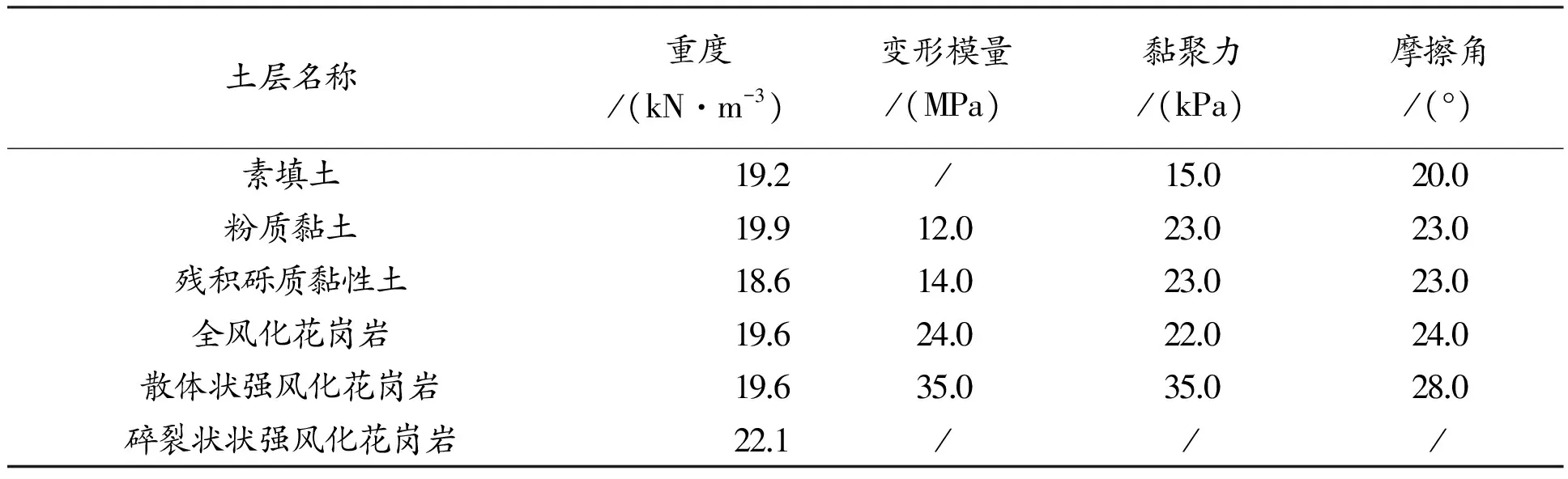
表1 地层参数

4.3 有限元分析

为分析管道沉降控制标准值的有效性，根据LNG管线所处地层的特性，建立了二维有限元模型，模型严格按照表1及图3中的地层参数，管道及管片均采用梁单元模拟，土层采用平面应变单元。所建模型的尺寸长为80 m，高为30 m，X方向为管道的纵向方向，即管道的纵向长度取80 m。

图4 管道垂直沉降 图5 管道沉降

图4给出了隧道开挖后管道的垂直沉降曲线。从图4可以看出：对于单线隧道开挖后，管道最大沉降为10 mm，最大沉降发生在隧道中心正上方；双线隧道开挖后，管道最大沉降为11 mm，最大沉降发生在双线隧道中心某处。通过有限元分析结果与理论计算得到的沉降控制标准进行对比发现，隧道开挖后，管道的沉降均未超过所制定的沉降控制标准，即表明了所制定的沉降控制标准具有一定的适用性和有效性。

4.4 管线沉降监测

LNG管道埋深较大，采用人工探孔的方式在管道周边范围进行布点测设。深层点的埋设5m深，基本位于监测管线的深度，测得的数据较真实，可作为反映LNG管道的实际沉降值。

根据本文分析结果，将理论分析得到的最大沉降量13.5 mm作为LNG管线的沉降控制标准，实际监测结果及计算结果对比见图5。

通过管道理论沉降分析、数值模拟以及现场监测结果分析可知，数值模拟与现场监测数据基本吻合，最大沉降发生在双线隧道中心线附近，最大沉降为12.62 mm，且未超过理论分析得出的管道沉降控制标准。说明本文分析得出的管道沉降控制计算公式基本合理可靠。

5 结语

本文结合规范给出的最小曲率半径计算方法和修正的沉降槽宽度计算公式，提出了隧道下穿高压管道的沉降控制标准理论计算方法，通过本文的分析可以得到以下结论：

(1)对在役高压及超高压管道，应着重考虑运营阶段的安全性和完整性，对于弹性敷设管道沉降后曲率半径应按公式(4)的要求且应考虑在自重作用下的管道转角。

(2)经理论推导，在役高压、超高压管道理论沉降量与管道的曲率半径及管道发生沉降后的沉降槽宽度有关，本文建议对高压及超高压管道的沉降控制标准应按照公式(18)给出的结果，以此作为高压、超高压管道的沉降控制标准。

(3)计算与实测结果表明：LNG管道的沉降并未超过沉降控制标准。通过该工程管道沉降的安全性评价，进一步表明了本文制定的高压及超高压管道沉降控制标准值的有效性，为类似工程提供了较为全面的参考。

(4)在实际监测中，本文建议应当将规范规定管道的允许曲率半径和允许最大沉降量同时作为高压及超高压管道的变形控制标准，能有效保证管道处于安全可控状态。

[1] 中华人民共和国建设部. 输气管道工程设计规范:GB 50251-2015[S].北京:中国计划出版社,2015.

[2] 中华人民共和国建设部. 油气输送管道穿越工程设计规范:GB 50423-2013[S].北京:中国计划出版社,2013.

[3] 张竹清. 地铁盾构隧道下穿高压LNG(液化天然气)管线距离控制要求及沉降控制标准探讨[J].隧道建设, 2016, 36(5): 531-536.

[4] 向卫国. 隧道开挖引起地下管线变形和安全性状的研究[D].北京:中国铁道科学研究院, 2011.

[5] 张昊. 天然气埋地管道的允许变形沉降量计算[J].上海煤气, 2010(4):14-15,46.

[6] 韩煊, 李宁. 隧道施工引起地层位移预测模型的对比分析[J]. 岩石力学与工程学报, 2007, 26(3): 595-600.

[7] 韩煊,罗文林,李宁. 地铁隧道施工引起沉降槽宽度的影响因素[J]. 地下空间与工程学报, 2009, 5(6): 1188-1193,1219.

[8] 刘建航,侯学渊. 盾构法隧道[M]. 北京：中国铁道出版社, 1991.

[9] 阳军生,刘宝琛. 城市隧道施工引起的地表移动及变形[M]. 北京：中国铁道出版社, 2002.

[10] Knothe, S.Observations of surface movements under influence of mining and their theoretical interpretation [C]. In: Proc. European Conf. on Ground Movement. 1957：210-218.

[11] 杨志鸣, 苏耀军.在役天然气管道沉降控制值的分析探讨[J]. 中国市政工程, 2006(4):66-68,71,109.

Standard analysis of settlement control for tunnel crossing underneath high-pressure pipeline

ZHANG Yun-tao
(ChinaRailwayFirstSurveyandDesignInstituteGroupLtd.,Xi'an710043,China)

Cases of new subway tunnels crossing underneath high-pressure gas pipelines is increasing with the accelerated construction of metro tunnels and high-pressure gas pipelines. The Chinese specifications only describe the radius of curvature of the high-pressure pipeline control parameters. The settlement deformation has been widely used as control parameters have no sufficient theoretical background. Based on the curvature radius of elastic pipeline laying standard calculation formula and the modified settlement groove width formula, a settlement control standard calculation formula has been proposed, and combined with the model analysis and measured results, the reliability of the theoretical analysis is verified, which provides a theoretical formula for the reference similar crossing engineering.

tunnel; high-pressure pipeline; radius of curvature; settlement groove width; settlement standard

2017-03-06

张运涛(1988—)，男，陕西西安人，硕士，工程师。

1674-7046(2017)02-0033-07

10.14140/j.cnki.hncjxb.2017.02.007

U25

A