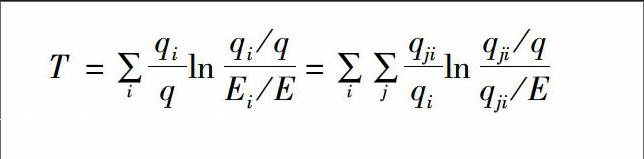中国二氧化碳的边际减排成本与区域差异研究

陈德湖　潘英超　武春友

摘要 测算二氧化碳的边际减排成本有利于评估区域碳减排潜力与成本，也是落实区域碳交易政策的重要依据。在多投入一多产出的生产效率模型框架下，本文采用二次型方向距离函数，研究了全国30个省份2000-2012年期间的碳边际减排成本及其差异的时空演化特征。二次型方向距离函数通过引用时间变量，反应环境治理的中性技术进步，因此研究方法能充分利用参数估计的灵活性。研究结果显示：①二氧化碳的边际减排成本平均约为1 519元/吨，远高于我国碳市场的交易价格，表明当前试点的自愿性碳交易政策是无效的；②区域碳边际减排成本的泰尔指数分解表明，东中西部地区的减排成本存在明显的地区性差异性，且随着时间的推进，碳减排空间逐渐变小。减排成本的地区性差异表明环境规制政策并不能保证各地区碳治理成本的边际均等原则，而利用政策工具，促使碳排放权从治理成本较高的地区转移至成本较低的地区，可以减少总治理成本，实现总量控制目标。本文建议：一方面，为实现国家碳减排的总体宏观目标，各区域要加强合作，相互借鉴成功的碳减排技术与经验等，在执行政策上，应尝试执行区域协同治理机制，努力降低总减排成本；另一方面，各区域在推进产业结构调整、城镇化及能源消费结构替代过程中要遵从循序渐进原则，避免碳减排成本过度波动，增加减排难度。

关键词 边际减排成本；方向距离函数；影子价格；减排空间

中图分类号 F062.2 文献标识码 A 文章编号 1002-2104（2016）10-0086-08 doi：10.3969/j.issn.1002-2104.2016.10.011

“十二五”期间，我国已批准北京市、天津市、上海市、重庆市、广东省、湖北省、深圳市7省市开展碳排放权交易试点，并计划于“十三五”期间实现覆盖全国31个省市自治区的碳排放交易体系。推行碳排放权交易已经成为国家经济体制和生态文明体制改革的重要任务之一。以市场手段配置碳减排配额，能有效减少碳排放总量，促进企业绿色技术创新，节约规制成本，激励企业参与减排行动，以更加有效的方式实现绿色低碳发展。

我国正处在向低碳社会转型的重要阶段，然而各地区的经济发展方式、技术水平、产业结构、资源禀赋、能源消费结构等不同，决定其碳减排代价或成本存在巨大差异，因此客观合理地评估碳减排的宏观成本与区域差异，有利于协调各地区经济发展与环境污染之间的关系，促进区域性环境协同治理体系的发展，也可以为企业参与碳交易提供政策依据。本研究以全国30个省市为例，首先，通过建立方向性距离函数，计算非期望产出与期望产出的边际转化率；其次，根据期望产出的價格，估算碳排放的影子价格；最后，用影子价格来衡量碳边际减排成本，并进一步分析碳减排成本差异的时空演化特征与其影响因素。

1文献回顾

二氧化碳排放一般是伴随生产或生活过程而产生，如火力发电企业在发电的同时，不可避免地产生二氧化碳、二氧化硫与氮氧化物等副产品。二氧化碳排放通常具有排放跨界性、危害全局性、经济上难以捕获与封存等特点，决定了碳排放的负外部成本很难测算。边际减排成本是指在一定生产技术水平下，减排主体每减少一单位碳排放带来的产出减少量或投入增加量。边际减排成本是企业的内部减排成本，因而边际减排成本及曲线可以帮助企业确定适当的减排技术与策略，也有助于环境管理部门评价区域、行业或企业碳排放的减排潜力、绩效与成本等。

利用经济模型估算非期望产出的影子价格，通常是指污染物或温室气体等副产品的虚拟价格或隐含价格，即边际减排成本。在传统的生产函数下，仅有一种产出（期望产出），因而更多的产出意味着更多的利润或福利。如果生产函数包含期望产出与非期望产出，当产出同时增减时，而非期望产出没有市场价格信息，此时社会福利很难测算。在多投入、多产出的生产效率模型下，利用距离函数与收入函数的对偶关系，估算两种产出的边际转换率，推倒出非期望产出的影子价格。

影子价格模型按照污染物作为投入还是产出，可分为投入距离函数与产出距离函数。投入距离函数利用成本最小化推导影子价格，而产出距离函数则利用收益最大化推导影子价格。环境经济理论一般认为，环境污染物是生产过程的副产品，而不应当作为投入要素，因此近年来产出距离函数在实证研究中得到广泛应用。产出距离函数按照函数形式不同又可以分为三种类型：谢泼德距离函数（Shephard）、双曲线距离函数、方向距离函数。谢泼德距离函数假定期望产出与非期望产出同时增加或缩减；方向距离函数非对称地处理期望产出与非期望产出，在缩减非期望产出的同时，增加期望产出；虽然双曲线距离函数也能非对称地处理期望与非期望产出，但它采用乘法形式，并不能完全分离出两种产出的内在关联性。

在估计方法上，现有的研究可分为三类：非参数数据包络法（DEA）、参数随机前沿法（SFA）与参数线性规划法（IJP）。非参数DEA法利用投入产出组合构建生产前沿并形成分段效率前沿面，其优点是不需要指定距离函数的具体参数形式，但该方法不能确保距离函数处处可微，因而有时难以计算影子价格。另外，利用DEA法估算影子价格受样本的奇异值影响较大，估计结果可能为负值等缺陷。参数SFA法利用计量模型估算距离函数，能够考察随机冲击和技术非效率因素对环境产出前沿的影响，也可以确保距离函数处处可微分，但是计量模型不能事先设定生产技术的约束条件，因此影子价格是否满足相关约束条件需事后评估。参数LP法继承了SFA方法的优点，并且可以更为灵活地设定约束条件求解影子价格，因此得到广泛应用。

在实证研究上，早期的研究主要集中在估算大气中的二氧化硫、氮化物或水污染物的影子价格，近年来随着气候变化问题成为关注的热点，越来越多的学者利用影子价格方法估计二氧化碳的边际减排成本。涂正革利用非参数方法估算了省际工业二氧化硫的影子价格，研究发现二氧化硫的影子价格取决于排放水平和生产率水平。袁鹏等利用采用二次型方向性距离函数对地级市工业部门的废水、二氧化硫和烟尘等三种污染物的影子价格进行了估计。刘明磊等采用非参数距离函数方法研究了能源消费结构约束下的我国省级地区碳排放绩效水平和二氧化碳边际减排成本。陈诗一利用参数化和非参数化两种方法对环境方向性产出距离函数进行估计，并测算了工业分行业的二氧化碳的影子价格。魏楚利用104个地级市的数据测算了城市二氧化碳的边际减排成本。

上述文献从不同角度研究了非期望产出的影子价格，但还存在以下可突破之处。首先，现有的研究多采用非参数方法估算非期望产出的影子价格，没能充分利用参数估计方法的灵活性。本文在方向距离函数的中引入时间虚拟变量，考虑到省际碳排放的中性技术进步影响。技术进步是提升碳排放效率的重要手段，也是减少碳排放的重要路径，忽视了技术进步对碳排放影子价格的影响，会造成影子价格估算偏误；其次，组建区域性碳排放交易市场的前提是碳边际减排成本存在区域差异，现有的研究没能对碳减排成本的区域差异进行深入分析，本文利用泰尔指数分解方法，研究了碳减排成本差异的时空演化特征。

2模型与估计方法

2.1方向距离函数与影子价格

方向性距离函数是谢泼德距离函数的一般形式，方向性距离函数具有参数灵活性等特点，近年来，在污染物影子价格估计上得到广泛应用。参照Fare的定义，假定投入x∈R^N₊，期望产出yx∈R^M₊，非期望产出b∈R^J₊，则生产技术定义为P（x）={（y，b）：x可以产生（y，b）}。产出集P（x）除了具备凸性、紧凑性与投入自由处置性等特点外，还必须满足以下性质：首先，期望产出与非期望产出具备零点关联性。如果（y，b）∈P（x）且y=0，意味着6=0。期望产出与非期望产出是联合生产的，污染物作为期望产出的副产品，如果没有污染物产出，就必须停产；其次，期望产出与非期望产出满足联合弱处置性。如果（y，6）∈P（x）且0≤θ≤1，则（θy，θb）∈P（x）。同比例地减少期望产出与非期望产出是可行的，换句话说，减少非期望产出必须要付出成本，其代价是相同比例地减少期望产出；最后，期望产出的自由处置性。如果（y，b）∈P（x）且y

在考虑到以上性质的基础上，本文设定方向性产出距离函数作为生产技术集：

（1）

其中g=（g_y，-g_b）为方向方量且g≠0。方向产出距离函数表明在给定的生产技术P（x）下，沿着向量g的方向，最大限度地扩张期望产出，同时缩减非期望产出，以达到产出前沿点。

非期望产出（如污染物）通常不能像商品一样进行市场交易，因此它没有价格。期望产出与非期望产出是联合生产的，根据方向距离函数的弱处置特点，缩减非期望产出必须相应地减少期望产出，因此，减少期望产出的价值可以看作非期望产出的机会成本，即影子价格。Fare根据产出距离函数与收益函数的对偶关系，利用謝泼德引理，推导出非期望产出与期望产出的影子价格比例等于其边际转化率，即

（2）式中，g是非期望产出的价格，p期望产出的价格，分式为非期望产出与期望产出的边际转化率。式（2）的含义是，污染物的价格等于减少一个单位的污染物，必须放弃相应期望产出变化的价值，也即污染物治理的影子价格或边际减排成本。如果方向性产出距离函数D是连续可微的，就可以利用期望产出的市场价格推导出污染物的影子价格。

2.2经验模型与求解

方向距离函数的参数形式通常有两种：超越对数函数与二次函数。超越对数的函数形式经常被用于谢泼德产出距离函数的参数化，正如前面所述，谢泼德产出距离函数通常把期望产出与非期望产出同等、对等，即通过同时扩张或同时缩减来计算产出效率与影子价格，因此不符合环境管制的要求。相比超越对数函数，二次函数的优点在于：二次函数满足方向距离函数的转移属性、二次可微性及灵活性等特性。理论研究也表明二次型函数在各种条件下均优于超越对数函数形式，Fare和Vardanyan等利用蒙特卡罗方法比较两类函数的性能发现，在不同的技术集条件下，无论是对于小样本还是大样本，二次型函数的估计结果要比超越对数函数的结果更为精确与灵活。

设定方向向量g=（1，-1），其含义表示，扩张期望产出的同时，同比例地减少非期望产出。本文在投入产出变量选择上，选择资本（x₂）、劳动（x₂）和能源（x₃）三种投入变量，期望产出为各地区的经济总产出（y），非期望产出为二氧化碳排放量（b）。因此，第k个生产单元t时期的二次型方向距离函数为：

（3）

考虑到距离函数中各生产单元的个体效益与时间效益的差异，在式（3）中的常数项加入省份虚拟变量与时间虚拟变量：

（4）

其中λ_k与τ_t为虚拟变量的系数。当k=k时，省份虚拟变量S_k'=1，否则S_k'==0。同理，当t=t时，时间虚拟变量T_t'=1，否则T_t'=0。

为求解方向距离函数的未知参数，我们采用参数线性规划的方法求解，目标函数是最小化各时期所有样本点与前沿点的离差和：

（5）

各约束条件下含义如下：条件①确保各决策单元在生产技术曲线的前沿面或内部，即满足方向距离函数的非负约束；条件②满足期望产出与非期望产出的零点关联性，即当非期望产出为零时，方向距离函数为负值，此时方向距离函数不可行。以往多数学者的研究是在估计参数后，对零点关联假设进行验证，本文则作为约束条件来估计参数以满足该特性；条件③与④是单调性约束，确保影子价格具备正确的符号；条件⑤是满足投入变量的自由处置性；条件⑥与⑦分别表示方向距离函数的转换属性和对称性。

3碳边际减排成本估计结果与区域差异分析

3.1数据与变量

本研究使用分省级面板数据，考虑到数据的可得性与完整性，选择2010-2012年期间全国30个省、市、自治区（不包括台、港、澳）作为样本估计碳排放的边际减排成本，其中西藏由于相关数据缺失，故予以删除。①投入。投入变量包括资本、劳动与能源三种。分省资本存量采用“永续盘存法”来估算，参考单豪杰的研究进行拓展，并以2000年为基期进行平减处理；劳动投入以各省份的三次产业就业人数的加总来表示；能源投入采用各地区一次能源消耗量，单位是万吨标准煤。②期望产出。采用分省份的地区生产总值，并以2000年为基期进行平减处理；③非期望产出。采用分省份的二氧化碳排放量。由于我国没有官方统计的二氧化碳排放量数据，本文估算各省主要化石能源消耗以及水泥生产过程的二氧化碳排放量，具体方法如下：

二氧化碳排放量根据IPCC《国家温室气体排放清单指南》（IPCC，2006）推荐的方法估算，选取煤炭、焦炭、汽油、煤油、柴油、燃料油和天然气7种主要化石能源，具体计算公式如下：

其中，C为估算的各类能源消费的二氧化碳排放量；i表示能源消费种类，E_i为各省份第i種能源的消耗量（实物量）；CF_i为各类一次能源的平均低位发热量；CC_i与COF_i分别是单位热值含碳量与碳氧化率COF_i；44/12为二氧化碳气化系数。除化石能源燃烧外，水泥生产过程中产生的二氧化碳排放约占总排量的10%左右，因此，在计算各省份的二氧化碳排放量过程中如果忽略了水泥工业生产中产生的碳排放（CE），会低估碳排放量。所以本文也利用各省份的水泥生产总量乘以水泥的碳排放系数来正确估计碳排放总量。

3.2估计结果与分析

本文采用GAMS/MINOS求解器求解线性规划模型（1）的未知参数，并计算方向性距离函数D与边际减排成本q。为了克服线性规划求解中的收敛问题，我们利用样本中投入产出的均值对所有变量进行了标准化处理。标准化处理后的数据意味着投入产出集（x，y，6）=（1，1，1），即对一个代表性省份，用平均投入获得平均产出。另外，在求解模型（1）得到参数后，由于数据事先进行了标准化处理，因此边际减排成本应当乘以投入产出均值以恢复其原有的减排成本规模。方向性距离函数的参数估计结果如表1所示。

从表1的参数估计结果可以看出，期望产出（y）的一阶系数为负值，负的系数表明地区生产总值越高，区域的环境无效率值越低；非期望产出（b）的一阶系数为正值，说明碳排放越多，环境无效率值越高；资本劳动与能源投入变量的一阶系数估计值均为正，表明投入越多，无效率值越高。投入产出的系数估计值均符合经济意义。时间虚拟变量的参数估计值均为负值，系数从2001年的-0.015 7减少到2009年的-0.076 6，且在2001-2009年期间逐渐下降，仅在近三年有所上升，表明各省份的环境技术随时间在逐步提升，无效率值逐渐减少，但近年来由于经济下行压力增大，环境技术进步率在下降。

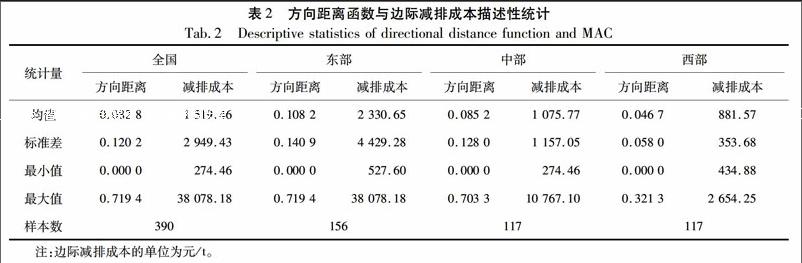
根据表2的方向性距离函数描述性统计，方向距离函数的均值是0.082 8，意味着平均而言，生产无效值为8.28%，也即在保持期望产出8.28%的提升空间同时，碳排放可以有8.28%的减排空间。更进一步，在本文的样本中，地区GDP平均值为7 790.27亿元，碳排放均值为2.32亿吨，因此，通过提升生产与减排效率，可以平均增加产出645亿元（7 790.278.28%），同时减少0.19亿t（2.328.28%）的碳排放量。全国的碳平均边际减排成本为1 519.46元/t，从分区域看，东部地区最高，其次是中部，西部地区最低。各省份碳边际减排成本的标准差较大，表明各省份的减排成本存在很大的差异，例如，2003年山西的碳减排成本为274.46元/t，为最低值，而2012年江苏的碳减排成本高达38 078.18元/t。地区性的碳减排成本的差异，进一步说明可以通过区域生态环境协同治理机制实现区域内生态环境治理系统之间良性互动，以达到减排成本最小化的目的，并形成整体的协同治理效应。

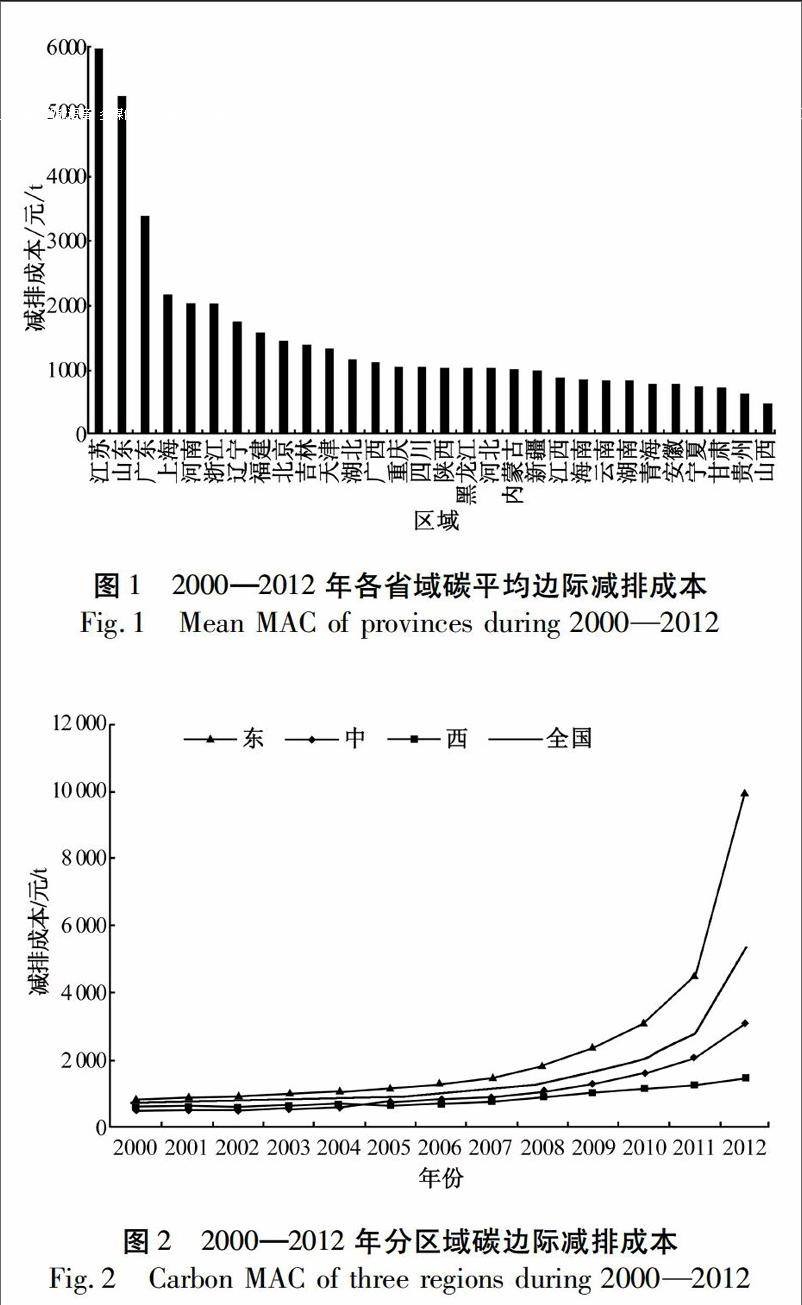
图1是各地区的平均碳边际减排成本的分布图，从图中可以看出，东部地区的江苏、山东和广东的减排成本均超过3 000元/t，中部的山西边际减排成本最低，为484.8元/t。西部地区中贵州、甘肃、宁夏的平均边际减排成本均低于800元/t。平均而言，东部地区的碳边际减排成本最高，其次是中部，西部最低。边际减排成本的地区性差异表明可以用市场化手段如区域性碳排放权交易体系等控制总量排放，实现减排成本最小化、效益最大化。以京津冀协同治理为例，京津冀三地均面临着严峻的环境治理形势，如果执行区域性碳排放权交易，则三个地区的总减排成本将下降。北京、天津与河北的碳边际减排成本分别为1 461元/t、1 343元/I、1 042元/t，以三个地区的平均边际减排成本作为碳交易价格，则三地区平均每交易1 000 t的碳排放权，则北京可以平均节约治理成本17.9万元，天津节约6.1万元，河北则获得24万元的减排收益。

再来分析地区性边际减排成本的时间演化趋势。如图2所示，在2000-2006年期间，东中西部的边际减排成本变化趋势非常一致，均缓慢增长。但2006年之后，各区域的边际减排成本快速增加，特别是东部地区从2006年的1 280元/t快速增至2012年的10 021元/t，中部地区增速稍低，从2006年的701元/t增至2012年的3 103元/t。与东中部相比，西部地区的边际减排成本较低，增速也较慢，2006年为781元/t，到2012年达到1 499元/t。这些数据表明国家环境保护的“十一五”规划首次提出建设环境友好型社会，以及“十二五”规划提出推进生态文明建设等一系列改革方针对不同区域的环境治理与经济发展有着不同的影响。东部发达地区经济发展基础较好，落实政策方针较为迅速，因此边际减排成本增长较快。而中西部地区以经济发展为重点，而且承接东部地区的产业转移和污染转移，对污染治理重视不够等，因此边际减排成本增速较慢，只是近年来随着人们对环境污染事件越来越关注，以及区域环境协同治理政策的开展，中西部的碳减排成本在逐渐增加。

结合各地区能源消费结构中的煤炭消费比重和第三产业结构比重的时间演化特点，可以分析各区域碳减排空间与减排难度的地区性差异。根据统计数据，东部地区的江苏、广东、上海等地区的煤炭消费比重分别从2000年的34%、23%、19%下降到2012年的19%、19%、9%；而碳边际减排成本最低的贵州、山西煤炭消费强度均超过40%。东部地区的第三产业结构比重从2000年的42%上升到2012年的47%，中部地区则从39%下降至36%，西部地区则从41%下降至39%。其中北京的第三产业结构比重最高，达到76%，广东、江苏等地区的第三产业结构比重均超过45%。这些数据表明，东部发达地区碳边际减排成本普遍较高，减排空间有限，仅依靠调整化石能源消费结构或压缩高排放高耗能行业等手段进行减排的难度比较大，未来需要通过技术进步及增加新能源的消费比重来减少排放；中西部地区经济发展水平和技术水平较低，能源利用效率不高，碳边际减排成本较低，因此可以通过建立跨区域的碳排放交易体系，进一步学习先进地区的生产技术和治理技术，提高能源利用效率有效减少化石能源消费量，促进第三产业发展等方式以达到减缓碳排放的目的。

3.3碳边际减排成本区域差异的泰尔指数分解

为了进一步分析碳边际减排成本的区域性差异与变动幅度，本文选择泰尔指数来衡量边际减排成本的区域差异。泰尔指数可以将区域间的总体差异分解为区域内差异和區域间差异两部分，因此可以揭示区域内差异和区域问差异及各自变动的方向与变动幅度，也能解释各自在总差异中的重要性及其影响。泰尔指数数值区间为[0，1]，数值越小，则说明地区差异越小；数值越大，则说明地区差异越大。计算泰尔指数首先要设定一个权重，考虑到碳减排成本的特点，本文选择各地区的碳排放量作为权重。泰尔指数的计算与分解公式如下：

式中，q_ji和E。分别表示第j区域第i省市的碳边际减排成本和碳排放量；T、T_w与T_b分别是计算出的总体、区域间与区域内泰尔指数；为进一步研究区域间差异和区域内差异对总体差异贡献的大小，分别设定区域间贡献率和区域内贡献率：区域间贡献率为区域间泰尔指数与总体泰尔指数的比值T_b/T；区域内贡献率为区域内泰尔指数与总体泰尔指数的比值T_w/T。另外，定义区域内各子区域的贡献率为加权后各子区域的泰尔指数与总体泰尔的比值（q_i/q）·（T_wi/T）。泰尔指数计算结果见图3和表3。

图3是三大区域碳边际减排成本的泰尔指数演化趋势，从图中可以发现三个区域的泰尔指数呈现不同特征。总体上看，东部地区的泰尔指数最高，其次是中部，最低为西部。东部地区在2000-2005年间稳步上升，边际减排成本区域内差异呈扩大之势，2005年之后差异保持平稳；中部地区泰尔指数呈先升后降的趋势，特别是至2003年达到峰值之后逐渐收敛，说明中部地区各省份碳边际减排成本差异在不断缩小；西部地区在整个研究时间段泰尔指数保持相对平稳状态，西部各省份的边际减排成本差异较小。

从表3可以看出，碳边际减排成本的泰尔指数表明我国东中西部地区的减排成本存在明显的地区性差异性。区域内泰尔指数均远大于区域间泰尔指数，区域内贡献率均在70%以上，且变动幅度不大，表明碳减排成本总体差异主要是由地区内差异带来的。在地区内差异中，中部和西部地区差异对总体差异贡献率较小，而且东部地区差异的对总体差异的贡献率呈上升态势，中西部的贡献率呈下降态势。

4结论与启示

中国目前是世界上碳排放量最大的国家之一。为了切实实现碳减排目标，“十三五”规划确定，到2020年，实现单位GDP二氧化碳排放量累计降低18%。我国政府采用多种手段与措施来实现既定的宏观减排目标，其中，碳排放权交易兼有环境质量保障和成本效率的特征，是近年来环境政策中一项极有特色的改革，成为总量控制下最有潜力的环境政策。我国已正式批准北京市、天津市、上海市、重庆市、广东省、湖北省、深圳市7省市开展碳排放权交易试点。然而，二氧化碳排放通常具有排放跨界性、危害全局性、经济上难以捕获与封存等特点，决定了碳排放的负外部成本很难测算。因此，估算碳排放的边际减排成本，可以为环境管理部门与参与企业提供有价值的成本信息，有利于改进碳交易规则，制度适当的碳减排策略。

考虑到碳减排的中性技术进步及区域异质性等因素，本文采用二次型方向距离函数，研究了全国30个省份2000-2012年期间碳边际减排成本及其区域差异性。通过本文的研究可以得出以下结论与启示：

第一，在研究的整个时期内，保证经济与环境协调发展的前提下，全国平均每年能减少8.28%的碳排放总量，碳排放的影子价格平均为1 519.46元/t，远高于当前我国碳市场的交易价格，表明我国当前的碳交易市场价格过低，市场交易效率低下。其原因是多方面的，当前我国碳交易市场仍处于试点阶段，并且采取自愿性交易的原则，交易对象多为高耗能的工业企业，交易不活跃等因素制约了碳市场的交易效率。

第二，二氧化碳边际减排成本区域差异较为明显，东部发达地区的减排成本要显著高于中西部地区。泰尔指数分解表明，在区域内，各省市的碳边际减排成本也存在较大差异。而且随着时间的推移，各地区的边际减排成本也显著上升，表明各地区的减排压力与难度逐渐增大，减排空间逐渐减少。因此，为实现国家碳减排的总体宏观目标，各区域要加强区域合作，相互借鉴成功的碳减排技术与经验等。在政策上，尝试执行区域协同治理机制，努力降低总减排成本。同时，各区域在推进产业结构调整、城镇化及能源消费结构替代过程中要遵从循序渐进原则，避免碳减排成本过度波动，增加减排难度。

（编辑：尹建中）