用改进的Chebyshev函数提高干涉图切趾效果*

江峰，武高卫，盛文，丰骁，冯至

(空军预警学院， 湖北 武汉 430019)

用改进的Chebyshev函数提高干涉图切趾效果*

江峰，武高卫，盛文，丰骁，冯至

(空军预警学院， 湖北 武汉 430019)

针对Chebyshev切趾函数在低旁瓣衰减时功率泄漏率高以及旁瓣衰减的等波动性问题，提出了一种改进的Chebyshev切趾函数。首先通过仿真分析指出Chebyshev切趾函数在光谱复原中存在的缺陷；然后选取Blackman-Harris函数对其进行改进，并与改进前进行了对比分析；最后，用该函数对单色光干涉图进行切趾处理并仿真验证，仿真结果表明，改进后Chebyshev切趾函数能够较好地克服功率泄露率高及旁瓣衰减等波动性的问题，其应用能力也更加灵活。

Chebyshev；切趾函数；Blackman-Harris；干涉图；光谱复原；仿真分析

0 引言

在傅里叶变换光谱仪光谱复原的过程中，存在傅里叶变换需要无限的积分区间而实际光谱仪只能提供有限光程差的矛盾，这个矛盾会造成复原光谱存在旁瓣效应进而影响邻近的、微弱信号的测定，此时就需要将光谱仪的干涉图进行切趾处理，以消除或者减弱虚假的旁瓣，增强有用信号的被检测率[1-2]。切趾的普遍做法是在信号处理中用切趾函数乘以干涉图，迄今学界已经提出了众多的切趾函数，包括三角函数、Hamming函数、Blackman函数、KaiserBessel函数以及各种函数族[3]。切趾函数的选取一般要考虑以下原则[4]：

(1) 切趾函数的形式尽量简单，切趾计算过程方便，计算量小；

(2) 切趾处理后复原光谱主瓣尽量窄，以保证系统分辨率；

(3) 切趾处理后复原光谱旁瓣尽量低，旁瓣衰减率尽量高。

实际应用中，用形式简单的切趾函数处理干涉图容易丢失有用信号，在抑制旁瓣的同时，系统分辨率也会降低，因此，要综合考虑切趾函数性质以及系统要求，选取合适的切趾函数。在给定旁瓣高度下，Chebyshev切趾函数的主瓣宽度最小，满足切趾函数的最大震幅比准则[5]，同时其旁瓣衰减量可调节范围宽，是一种性能优异的切趾函数；但是当干涉图信号功率较弱，需要小的旁瓣衰减情形时，其主瓣功率泄露严重，在频域上表现为相位误差增大，并且由于旁瓣衰减的等波动性，旁瓣衰减速率为零，不利于临近强干扰信号的抑制。文献[6]对基于传统Chebyshev函数设计的滤波器相位特性较差的缺点进行了改进，牺牲幅度特性提升其相位特性；文献[7]针对其旁瓣衰减的等波动性，提出离散傅立叶变换后对旁瓣进行相位旋转，利用叠加校正的方法使旁瓣干扰降到最低，然而，这种方法在增加计算量、引入误差的同时，计算精度得不到保证。因此，本文提出一种改进的Chebyshev切趾函数，在保留Chebyshev切趾函数原有优点的基础上，通过引入Blackman-harris函数改善其旁瓣衰减的等波动性、低旁瓣衰减时主瓣功率泄露严重的问题，同时，新切趾函数第一旁瓣衰减的可调节性也更加灵活。

1 Chebyshev切趾函数及其分析

Chebyshev切趾函数是由Chebyshev多项式在单位圆上作等间隔抽样，再作DFT反变换得到的[8]。Chebyshev多项式定义为

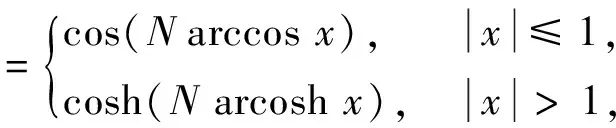
(1)

式(1)可以通过迭代产生：Tk+1(x)=2xTk(x)-Tk-1(x),T0(x)=1,T1(x)=x，其中x∈Z,k∈R且k≥1，令函数长度N=2M+1，则Chebyshev切趾函数在时域的表达式为

wC(n,γ)=

-M≤n≤M,

(2)

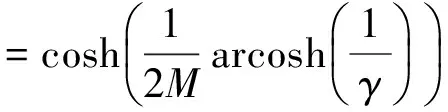
(3)

式中：γ为用分数表示的旁瓣与主瓣幅度的比值[9-10]，则第一旁瓣相对于主瓣衰减值m=20lgγ(dB)，在实际应用中，仅需调整γ的值就可以获得不同的主瓣宽度、旁瓣衰减等指标，Chebyshev切趾函数的性质如表1所示，与其他典型切趾函数的幅频响应对比如图1所示。

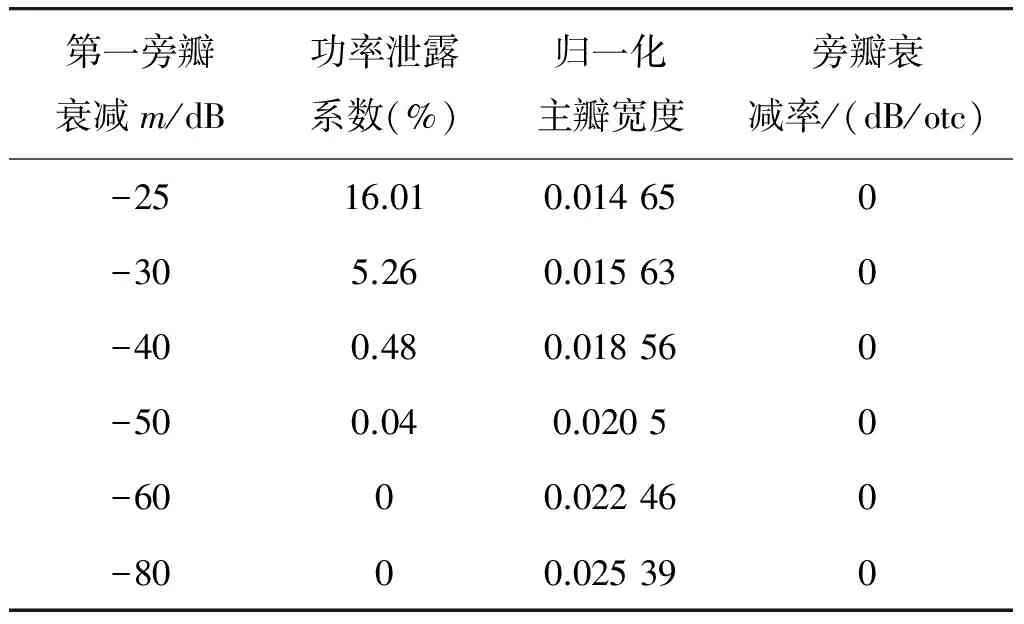
表1 Chebyshev切趾函数在不同旁瓣衰减时的性质(N=128)

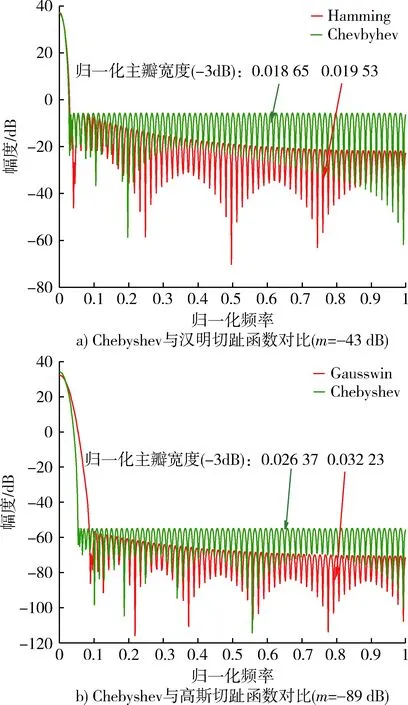
图1 Chebyshev切趾函数与两种典型切趾函数在相同旁瓣衰减下的对比(N=128)Fig.1 Comparison of Chebyshev apodization function with two typical apodization functions at the same side-lobe attenuation(N=128)

图1中，a)是Chebyshev切趾函数与Hamming函数(形式简单、切趾性能不可调)的对比，b)是Chebyshev切趾函数与Gausswin函数(形式复杂、切趾性能可调)的对比。通过图1可以发现，在相同第一旁瓣衰减情况下，Chebyshev切趾函数具有更窄的主瓣宽度，这使得干涉图经过Chebyshev切趾后光谱分辨率更高；同时，Chebyshev切趾函数第一旁瓣衰减可调节范围宽，具有更强的工程实用价值。然而通过表1可以发现，当旁瓣衰减较小时，Chebyshev切趾函数主瓣功率泄露严重，并且其旁瓣衰减率为零，不利于临近强干扰信号的抑制。为了更好地利用Chebyshev切趾函数的优点，对Chebyshev切趾函数的改进显得十分有必要。

2 改进的Chebyshev切趾函数及其分析

通过第1节对Chebyshev切趾函数的分析，在众多切趾函数中选取Blackman-Harris函数用于对Chebyshev切趾函数的改进。Blackman-Harris切趾函数是一种具有良好旁瓣性能的四项系数三阶余弦函数，与其他切趾函数相比，它具有以下优点：第1，作为一种余弦函数，其切趾运算简单易行[11]；第2，在同步误差较小时，旁瓣抑制能力强，通过在Matlab中调用Wvtool函数对其幅频响应进行分析，发现其旁瓣电平相对于主瓣可降低-92 dB[12]，能较好的适应Chebyshev切趾函数旁瓣衰减调节范围宽的特点；第3，Blackman-Harris函数有一定的旁瓣衰减率，对Chebyshev切趾函数旁瓣衰减率的提高具有改善作用。Blackman-Harris函数表达式可由余弦窗的一般表达式推导得出：

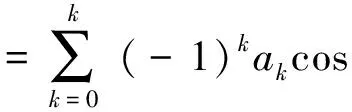
(4)

式(4)为余弦窗的一般表达式，其中0≤n≤N-1，k为项数。当k=0时，式(4)为矩形切趾函数，当k=1时，为汉宁切趾函数，当k=2时，为Blackman切趾函数，k=3时，为Blackman-Harris函数。长度为N的Blackman-Harris函数其时域表达式为[12-13]

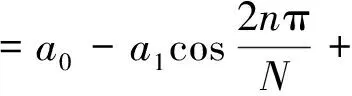
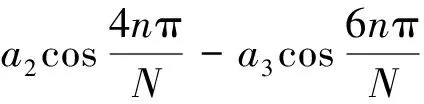
(5)

式中：a0=0.358 75,a1=0.488 29,a2=0.141 28,a3=0.011 68。为此，在原有可调参数γ的基础上，增加了可调参数L(0≤L≤N)，对Chebyshev切趾函数进行改进：

wC_B_H(n,γ,N,L)=

(6)

式(6)为改进后的Chebyshev切趾函数时域表达式，其波形如图2所示(N=128,L=80)，改进的Chebyshev切趾函数同时拥有Chebyshev与Blackman-Harris函数的优点，通过Matlab计算，其性质如表2所示。

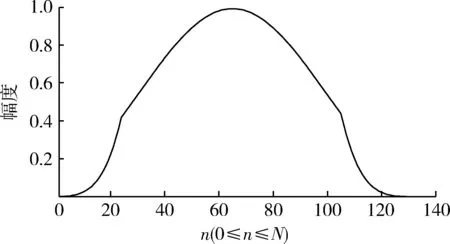
图2 改进的Chebyshev切趾函数Fig.2 Improved Chebyshev apodization function

表2 改进的Chebyshev切趾函数在不同旁瓣衰减时的性质

Table 2 Property of improved Chebyshev apodization function at different side-lobe attenuation

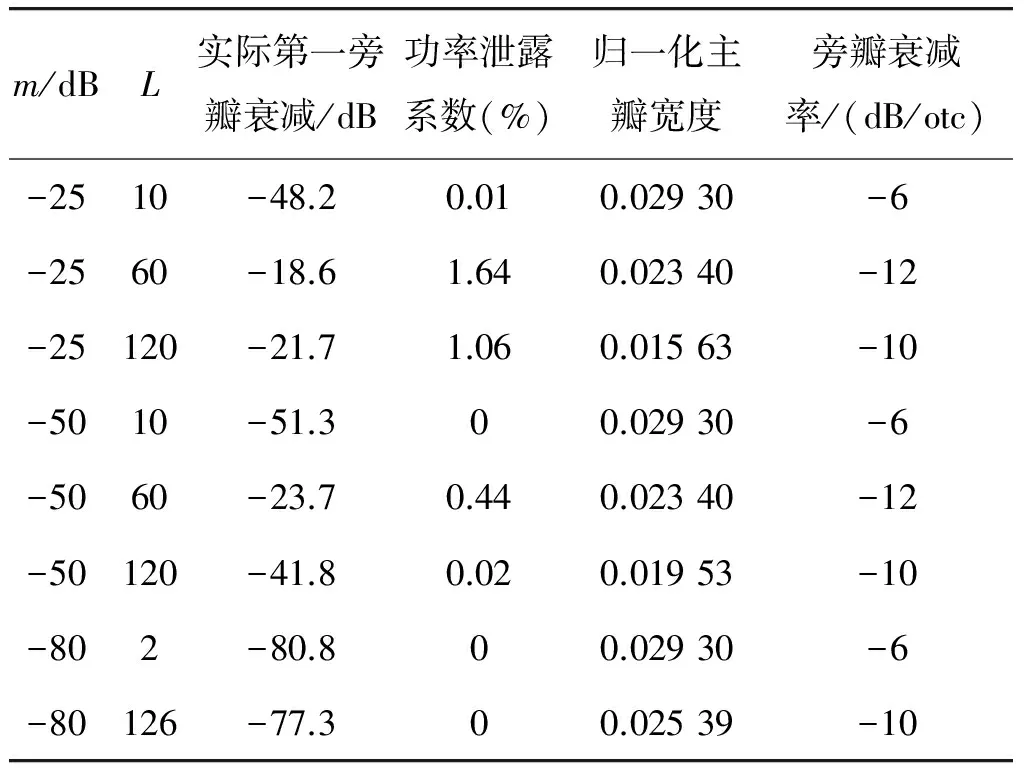
m/dBL实际第一旁瓣衰减/dB功率泄露系数(%)归一化主瓣宽度旁瓣衰减率/(dB/otc)-2510-48．20．010．02930-6-2560-18．61．640．02340-12-25120-21．71．060．01563-10-5010-51．300．02930-6-5060-23．70．440．02340-12-50120-41．80．020．01953-10-802-80．800．02930-6-80126-77．300．02539-10

通过表1和表2的对比可以发现在实际旁瓣衰减较小时，改进后切趾函数功率泄露系数得到了明显的改善，同时通过调节参数L，其仍可以保留Chebyshev切趾函数归一化主瓣宽度较窄、第一旁瓣衰减调节范围宽等优点，并且旁瓣衰减率得到了增加。改进的切趾函数与原Chebyshev切趾函数的幅频响应对比如图3所示。

图3中，a)为改进的切趾函数与Chebyshev切趾函数在第一旁瓣衰减43 dB时的比较，其中L=127，m=-46 dB,改进的切趾函数功率泄露系数为0.07%，原Chebyshev切趾函数为0.23%。b)为改进的切趾函数与原Chebyshev函数在第一旁瓣衰减25 dB时的比较，其中L=127，m=-27 dB，改进的切趾函数功率泄露系数为5.89%，原Chebyshev切趾函数为16.01%。c)为改进的切趾函数与原Chebyshev函数在第一旁瓣衰减25 dB时的比较，其中L=101，m=-38 dB, 改进的切趾函数功率泄露系数为0.4%，原Chebyshev切趾函数为16.01%，改进后函数旁瓣衰减率达到了12 dB/otc。

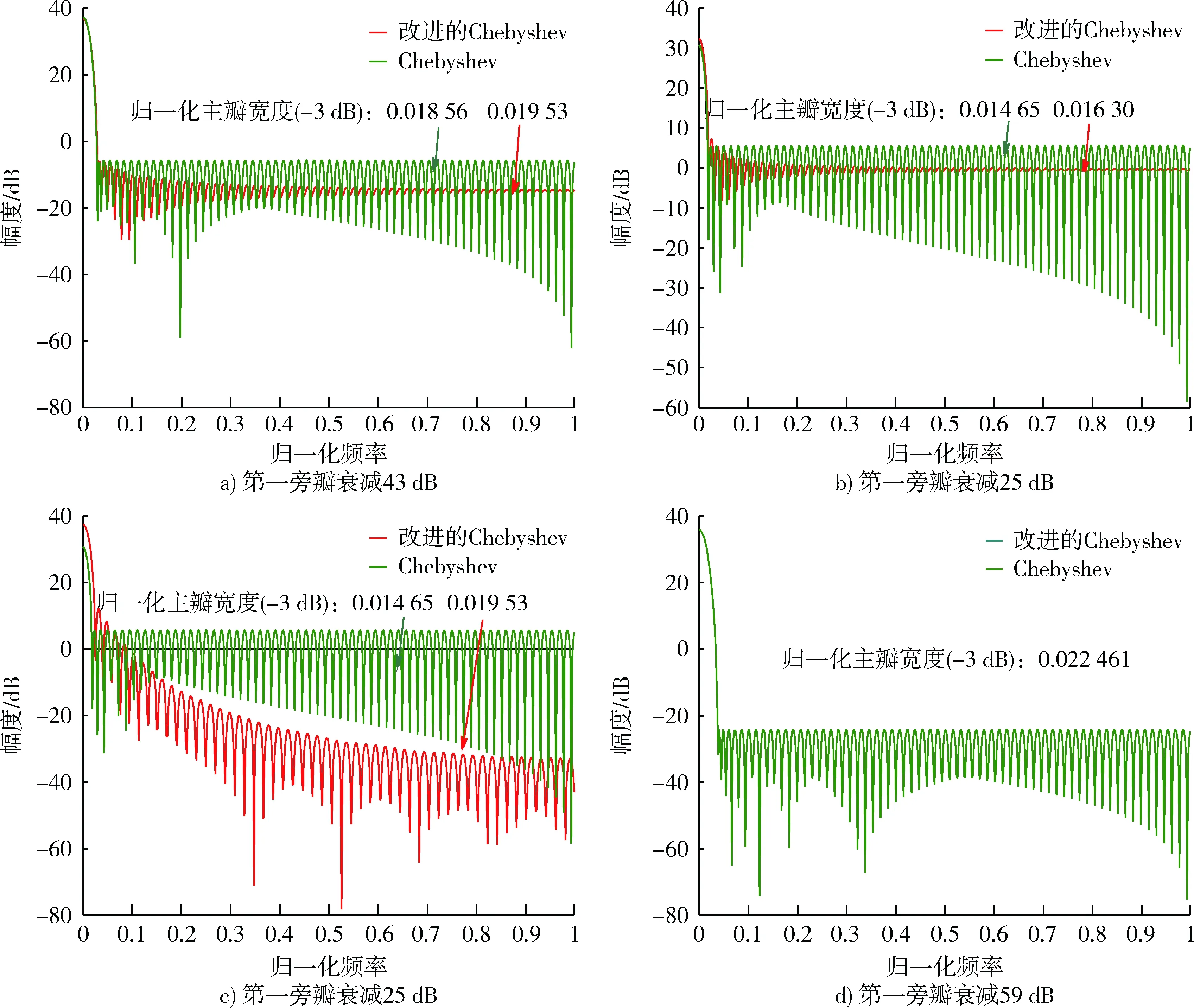
图3 改进的切趾函数与原Chebyshev切趾函数在相同旁瓣衰减下的比较(N=128)Fig.3 Comparison between the improved apodization function and the original Chebyshev apodization function under the same side-lobe attenuation (N=128)

从图3a)，b)，c)的结果可以看出，通过对参数γ及参数L的调节，新的切趾函数在功率泄露系数、旁瓣衰减率方面得到了很大的改善，从图3b),c)可以看出，不同的γ及L值可以得到相同的第一旁瓣衰减，但功率泄露系数、旁瓣衰减率和主瓣宽度会有相应的增减，这使得改进的Chebyshev切趾函数可以适应不同的切趾要求，应用能力更加灵活。在一般情况下，其主瓣宽度较原Chebyshev函数有所增宽，但是当取L=N时(图3d)，改进的切趾函数恢复原Chebyshev函数的效果，主瓣宽度最窄。

3 仿真与讨论

为进一步验证改进型切趾函数的性能，选取余弦波模拟单色光的干涉图，首先在Matlab中生成余弦信号，对此信号采样(采样频率100 Hz，采样点数512点)，然后进行切趾、光谱还原处理。则系统理想干涉图为

IR(x)=100 cos(2π·4x).

(7)

限制于干涉仪只能提供有限的光程差，实际截断干涉图为

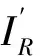
(8)

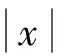
式(8)经过反傅里叶变换，即可得到矩形函数切趾后的光谱图[14]：

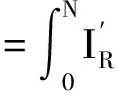
(9)

式中：σ为光谱波数；BR(σ)表示波数σ处的光谱强度。

然后用改进的切趾函数和4种典型切趾函数乘以式(8)，对实际干涉图切趾后进行式(9)的变换，得复原光谱如图4所示。

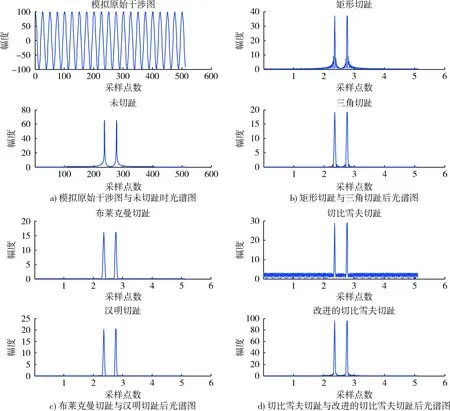
图4 几种典型切趾函数对单色光干涉图切趾还原后光谱图效果对比Fig.4 Contrast effect of restored spectrum of monochromatic light from several typical apodization functions

图4中，a)为模拟原始干涉图及其未经切趾处理的复原光谱，b)为矩形切趾及三角切趾后的复原光谱，实际应用中，限制于光谱仪只能提供有限的光程差，矩形切趾后的干涉图即为一般意义上的原始干涉图[15]，从图b)可以看出，经矩形切趾后的复原光谱旁瓣衰减不足，经三角切趾后的复原光谱旁瓣虽然得到了一定的抑制，但是主瓣宽度增加较多，光谱分辨率下降明显；c)为布莱克曼与汉明切趾后的复原光谱，旁瓣抑制能力进一步增强，但仍然存在主瓣宽度增加明显的问题，切趾处理后光谱还原效果并不理想；d)中，2种切趾函数在相同的第一旁瓣衰减下(-25 dB)，改进的Chebyshev切趾函数旁瓣抑制能力较强，旁瓣衰减率得到了提高的同时，主瓣宽度增加并不明显，因此，改进后的Chebyshev函数是一种性能优异的切趾函数。

4 结束语

本文对傅里叶变换光谱仪干涉图切趾函数进行了研究，提出了改进的Chebyshev切趾函数，利用Chebyshev切趾函数切趾处理后光谱图主瓣宽度窄、旁瓣衰减可调节的优点与Blackman-Harris切趾函数旁瓣衰减能力强，具有一定旁瓣衰减率的特点相结合，对Chebyshev切趾函数进行了改进。将改进后的切趾函数进行分析与仿真验证，结果表明：①改进后的Chebyshev切趾函数较正了原切趾函数旁瓣衰减较低时，功率泄露严重的问题；②改进后的Chebyshev切趾函数较正了原切趾函数旁瓣等波动性，旁瓣衰减率为0的问题；③改进后的Chebyshev切趾函数相比于原切趾函数更加灵活，可以在相同第一旁瓣衰减量下得到不同的功率泄露效果、旁瓣衰减率和主瓣宽度。

[1] 肖青，柳钦火，李小文，等.高分辨率机载遥感数据的交叉辐射影响及其校正[J].遥感学报，2005(6): 3-11. XIAO Qing, LIU Qin-huo, LI Xiao-wen,et al. Analysis and Correction of Atmospheric Cross Radiation for High Geometric Resolution Airborne Remote Sensing Data[J].Journal of Remote Sensing, 2005(6): 3-11.

[2] 李苏宁，朱日红，李建欣，等.傅里叶干涉成像光谱技术中的重构方法[J].应用光学,2009,30(2):268-272. LI Su-ning, ZHU Ri-hong, LI Jian-xin,et al. Method of Reconstruction on Fourier Transform Spectroscopy[J].Journal of Applied Optics, 2009,30(2):268-272.

[3] 景娟娟，相里斌，吕群波，等.干涉光谱数据处理技术研究进展[J].光谱学与光谱分析,2011,31(4):865-870. JING Juan-juan, XIANG Li-bin, LÜ Qun-bo,et al.Advance in Interferogram Data Processing Technique[J].Spectroscopy and Spectral Analysis,2011,31(4): 865-870.[4] 杨琨. 傅里叶变换红外光谱仪若干核心技术研究及其应用[D]. 武汉：武汉大学，2010: 20-21. YANG Kun. Research and Application on a Certain Number of Core Technologies of Fourier Transform Infrared Spectrometer[D]. Wuhan: Wuhan University, 2010: 20-21.

[5] 《数学辞海》编辑委员会. 数学辞海(第三卷)[M].北京:中国科学技术出版社，2002:373. Mathematic Dictionary Editorial Board. Mathematic Dictionary(Volume III)[M]. Beijing: China Science and Technology Press,2002:373.

[6] 王晓凯，李锋.Chebyshev 过渡型滤波器设计和分析[J].信息与电子工程，2009,7(2):115-118. WANG Xiao-kai, LI Feng. Design and Analysis of Chebyshev Transitional Filters[J]. Information and Electronic Engineering, 2009,7(2):115-118.

[7] 孙仲民，黄俊，杨键维，等. 基于切比雪夫窗的电力系统谐波/间谐波高精度分析方法[J]. 电力系统自动化，2015, 39(7)：117-122. SUN Zhong-min, HUANG Jun, YANG Jian-wei,et al. A High Accuracy Analysis Method for Harmonics and Inter-Harmonics in Power Systems Based on Dolph-Chebyshev Windows[J]. Automation of Electric Power Systems, 2015, 39(7)：117-122.

[8] 谢俊好，杨曦.天线阵角分辨率准则的比较研究[J].雷达科学与技术，2010,8(4):382-389. XIE Jun-hao, YANG Xi. Comparative Research on Angular Resolution Criteria for Antenna Array[J]. Rafar Science and Technology, 2010,8(4):382-389.

[9] OPPENHEIM A V，SCHAFER R W，BUCK J R. 离散时间信号处理[M]. 2版.刘树棠，黄建国,译. 西安：西安交通大学出版社,2001. OPPENHEIM A V,SCHAFER R W,BUCK J R.Discrete-Time Signal Processing[M].2nd ed.LIU Shu-tang,HUANG Jian-guo,translated.Xi’an Jiaotong Uni versity Press,2001.

[10] MITRA S K. 数字信号处理——基于计算机的方法[M].3版. 孙洪，译. 北京: 电子工业出版社，2006:435-436. MITRA S K.Digital Signal Processing——A Computer-Based Aproach[M]. 3rd ed. SUN Hong，Translated，Beijing: Elecronic Industry Press,2006:435-436.

[11] 赵文春，马伟明，胡安.电机测试中谐波分析的高精度FFT算法[J].中国电机工程学报，2001, 9(12) : 83-87. ZHAO Wen-chun, MA Wei-ming, HU An. FFT Algorithm with High Accuracy for Harmonic Analysis in the Electric Machine[J]. Proceedings of the CSEE, 2001, 9(12) : 83-87.

[12] 刘海升，付志红，张淮清，等.基于Blackman-Harris相位差校正信号谐波分析方法[J].数据采集与处理，2011,26(4):468-472. LIU Hai-sheng, FU Zhi-hong, ZHANG Huai-qing,et al. Harmonic Analysis Based on Blackman-Harris Window and Phase Difference Correction[J]. Journal of Data Acquisition and Processing,2011, 26(4):468-472.

[13] ZHANG F, GENG Z, YUAN W. The Algorithm of Interpolation Windowed FFT for Harmonic Analysis of Electric Power System[J]. IEEE Transactions on Power System, 2001,16(2):160-164.

[14] 尚博. 高光谱干涉成像重构技术研究[D]. 南京：南京理工大学，2008:23-24. SHANG Bo. The Study of Hyperspectral Imaging Interferometer Reconstruction[D]. Nanjing: Nanjing University of Technology and Engeneering, 2008:23-24.

[15] 韩刚. 干涉光谱复原算法研究[D]. 西安:中国科学院研究生院，2012:9-12. HAN Gang. Research on the Algorithm of Inteferogram Spectrum Reconstruction[D]. Xi’an: Chinese Academy of Sciences of Master of Engineering, 2012:9-12.

Improved Chebyshev Function to Raise the Effect of Interferogram Apodization

JIANG Feng, WU Gao-wei, SHENG Wen, FENG Xiao, FENG Zhi

(Air Force Early Warning Academy, Hubei Wuhan 430019, China)

In order to rectify the shortcomings of high power leakage rate at low side-lobe attenuation and identical fluctuation of side-lobe attenuation of Chebyshev apodization function, an improved Chebyshev apodization function is put forward. Firstly, the defects of Chebyshev apodization function in spectrum restoration is analyzed by simulation; and then, the Blackman-Harris function is selected to improve it and compared with the previous one; at last, the function is used for monochromatic interferogram apodization process and simulation. The simulation results show that the new Chebyshev apodization function can solve the problems of high power leakage rate at low side-lobe attenuation and identical fluctuation of side-lobe attenuation, and its application ability is more flexible.

Chebyshev; apodization function; Blackman-Harris; interferogram; spectrum reconstruction; simulation analysis

2016-04-05；

2016-07-10 作者简介：江峰(1992-)，男，四川眉山人。硕士生，主要研究方向为红外光谱复原技术研究。

10.3969/j.issn.1009-086x.2017.02.025

TN911.1；TH744.1

A

1009-086X(2017)-02-0160-06

通信地址：430019 湖北省武汉市江岸区黄浦大街288号空军预警学院研究生管理大队21队E-mail：969656256@qq.com