PID控制策略下空气悬架系统的仿真

马相飞，李凯

（长安大学 汽车学院，陕西 西安 710064）

PID控制策略下空气悬架系统的仿真

马相飞，李凯

（长安大学 汽车学院，陕西 西安 710064）

通过对空气悬架系统的分析，建立其数学模型，再结合二自由度空气悬架的运动学方程，在MATLAB/SIMULINK中搭建有无PID控制器的空气悬架系统仿真模型。使其在白噪声路面激励信号下进行仿真实验，实验结果表明PID控制策略下空气悬架能更好的降低车身垂直加速度，使车辆平顺性得到很好的改善。

空气悬架系统；SINULINK；PID控制

CLC NO.:U467.3 Document Code: A Article ID: 1671-7988 (2017)08-142-04

引言

悬架系统作为汽车车身和车轮的主要连接部件之一，使得作用于两者之间的力和力矩得到很好的传递，也让汽车的平顺性和操作稳定性得到了一定改善。伴随着科学技术和经济的发展，人们对汽车的平顺舒适性能有了更高的追求。空气弹簧悬架因其高度可调、刚度可变、噪声小等优势使得它在汽车上得到大量使用。同时为了使空气弹簧悬架的性能在车辆中得到更好的的应用，往往需要一定的控制策略。PID控制器因其适用性较强、简单易懂、使用方便等优势而被应用到各个行业领域中。文中通过对空气悬架系统及PID特性的分析，搭建了PID控制下的空气悬架系统模型，进而对悬架性能进行分析研究。

1、空气悬架系统

1.1 空气弹簧

空气悬架系统有空气弹簧、高度控制阀和传统悬架必有的元件所组成。而空气弹簧作为空气悬架系统最为核心的部件之一，人们对其研究也越来越重视。空气弹簧是在含有帘布层结构的橡胶气囊内充入空气，并以空气为介质，利用空气可以压缩的特点来实现弹性作用。空气弹簧的主要作用部件的材料为橡胶，由于其非线性弹性特性比较理想，进而不仅使得悬架动挠度减小，还使得悬架和车架撞击的概率大大降低。空气弹簧主要有膜式、囊式和结构介于囊式和膜式之间的复合式空气弹簧这三类。通过对比膜式和囊式空气弹簧可以发现，同尺寸及空气压力下，膜式空气弹簧的承载能力虽然小，但其刚度相对较低；而膜式与复合式空气弹簧相比，其制造工艺相对简单，成本比较低，所以目前对复合式空气弹簧的应用比较少[1]。本文所分析的悬架系统中的弹簧类型为膜式空气弹簧，如图1所示：

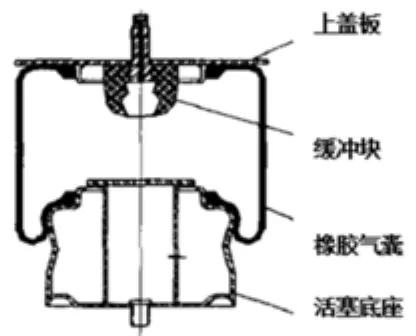
图1 膜式空气弹簧

1.2 空气悬架模型分析

1.2.1 膜式空气弹簧的数学模型

空气弹簧的承载力F是由空气弹簧内的所存储的气体和其有效支撑面积来决定的，其计算公式为：

而空气弹簧在实际振动过程中，由于其内部压强发生变化，使得有效工作面积发生改变，继而也引起有效容积发生变化，因此可以将有效面积和有效容积视为弹簧高度x的线性函数[2]，即：

对于空气弹簧内所存储的的气体，始终满足式（2-3）所给出的状态方程，即：

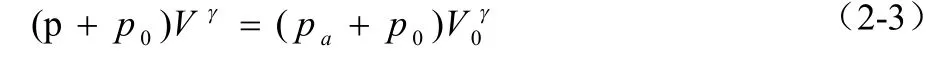
式中γ为多变指数。对于一般行驶中的车辆，汽车的振动既不激烈，也不缓慢，从而使得空气弹簧内存储气体的变化过程介于等温和绝热之间，此时γ=1.33[2]。

将以上几式进行整理可得膜式空气弹簧内部气体的终了状态气体压力为：

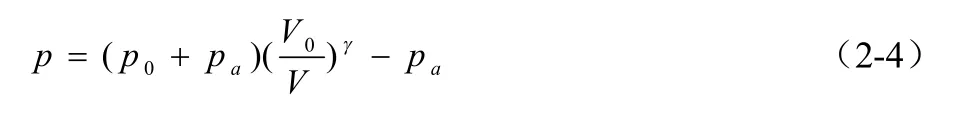
空气弹簧的弹力近似为：

空气弹簧的刚度则可由其弹力对位移求导得出，即：

1.2.2 空气悬架模型

汽车作为一个振动系统是非常复杂的，为了方便对问题的研究分析，应将其进行简化。同时为了使车轮和车身以较高频率振动时的特性得到较好的反应，我们可以将汽车简化成一个二自由度的振动系统；该系统能更加真实的对空气悬架系统的实际运行状况进行模拟，从而有效的分析其对汽车平顺性的影响，其模型如图2所示[3]。对模型进行分析得其运动方程为：

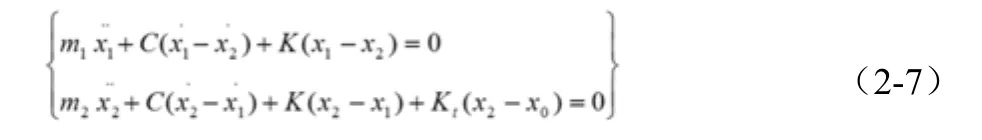
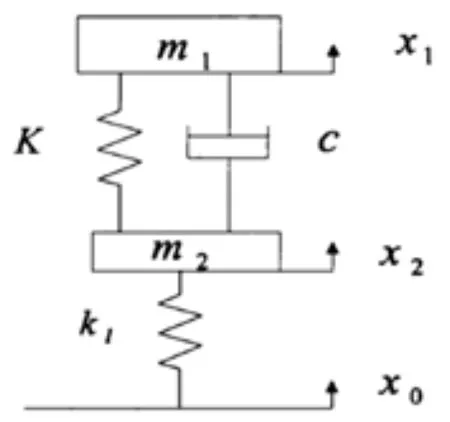
图2 二自由度1/4空气悬架模型

以上各式中的参数定义见表1：

2、路面模型的建立

路面纵断面曲线是指路面相对基准平面的的高度q的一个长度走向变化曲线。该变化曲线作为路面对车辆振动的一个激励信号，一般利用路面功率谱密度函数Gq（n）对其统计特性进行描述，并且常用下式作为拟合表达式[4]：式中，n为空间频率，n100.1-=m，W为频率指数，一般来说W=2。

我国按路面功率谱密度又把路面不平度分为了8级，而本文所研究的路面等级为B级。当我们对空气悬架系统进行分析时，应同时考虑路面激励和车速这两个因素，再由车速u、空间频率n和时间频率f的转换关系（f=u·n），将式（3-2）转化为时间频率功率谱密度G（qf）[5]。它们之间的转换关系式为：式中f为时间频率，单位为HZ；联立上述公式可得：有该式可得：

有此可得路面不平度速度的时域表达式，即：

当路面在较低频率范围内变化时，上述公式不能更好更真实的反应其情况，因此我们在公式中引入了一个因子---下限截止频率f0，其值一般取在0.0628hz附近，并且通过该频率建立滤波白噪声路面模型，从而使路面在低频范围内的情况得到更好的反应，其公式如下[6]：

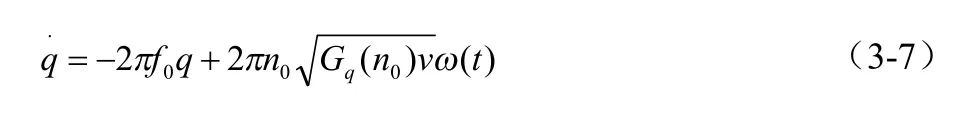
当车速为45km/h时，路面为B等级，由路面不平度分类标准可得路面不平度系数G(n)=64×10-6m2/m-1，从而应用

q0

simulink建立随机滤波白噪声路面模型，仿真模型如图3，仿真结果如图4。

3、基于1/4悬架系统的PID控制

3.1 PID控制器

PID（比例—积分—微分）控制器因其原理简单，使用方便灵活等优点成为各领域中应用比较广泛的一种控制器，并且以PID控制器作为基础还可以构成很多复杂的控制系统。基本的PID控制策略可以描述为下式：

图3 路面谱仿真模型

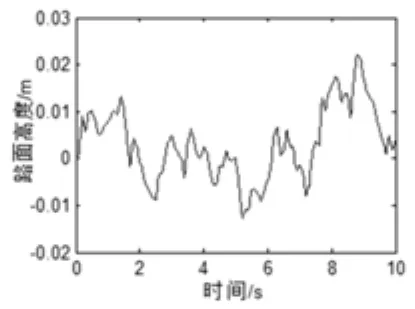
图4 路面仿真结果

式中：e(t )=Int(t)-y(t )；Kp为比例系数；T1为积分时间常数；TD为微分时间常数。

PID控制器的基本框图5如下：

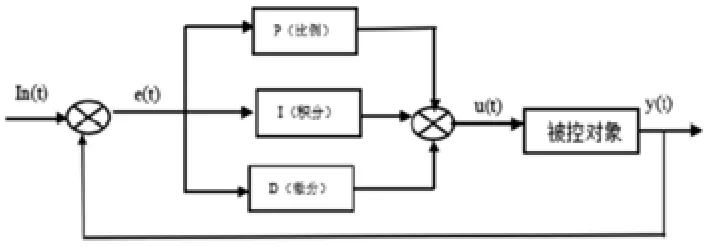
图5 PID控制器原理基本框图

本文选取空气弹簧的刚度K作为输出u(t)，比较信号y(t)为车身加速度，In(t)为0，然后根据上式搭建PID控制器的仿真模型。

通过对PID控制器中Kp、KI、KD三个参数进行调整确定，从而对仿真模型进行较为准确的控制。调整确定的方法总的来说包括两种，一种是根据理论计算进行调整确定，一种是根据工程经验进行调整确定，比较两种方法可以发现由第一种方法得到的结果需要根据工程实际在进行调整，而根据工程经验得到的结果可直接应用，且原理比较简单，容易计算和掌握[7]。本文根据工程经验公式，结合空气悬架的特性，再利用试凑法确定出PID参数。其确定步骤是先整定比例参数，然后加入积分环节，调整确定积分系数，最后加入微分环节，构成PID控制器[8]。经过多次的运行仿真所确定参数分别为：Kp=1300，KI=60；KD=2。

3.2 PID控制下的空气悬架二自由度振动模型

图6 基于PID控制器的空气悬架仿真模型

图7 空气悬架模型

根据上述论述中所得出的基本数学模型，应用MAT LAB/simulink搭建PID控制下的空气悬架二自由度振动模型并进行仿真分析。整个空气悬架模型的输出为Kt(X2—X0)，它们分别对应车身垂直加速度、悬架动挠度、车轮动载荷三个参数，而一个悬架性能的好坏通常有这三个参数进行确定[9]。搭建好的空气悬架模型如图6和图7所示。

4、空气悬架系统的仿真结果分析

根据上文搭建好的空气悬架仿真模型，在白噪声路面激励信号下，对有无PID控制器的空气悬架进行仿真，仿真时长设为20s，仿真模型的选取参数如表2所示，仿真结果如图8、9、10所示：

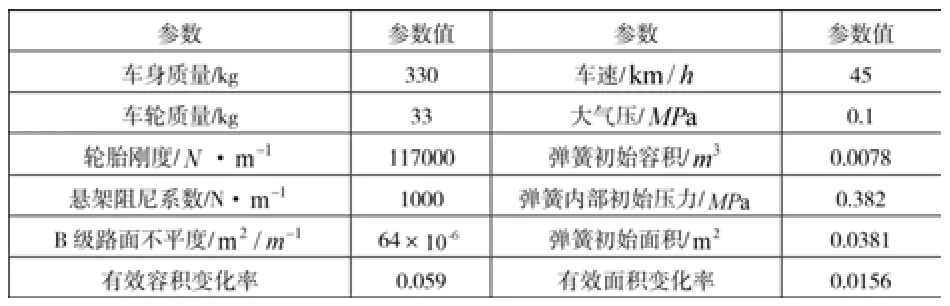
表2 模型参数

图8 车身垂直加速度仿真曲线

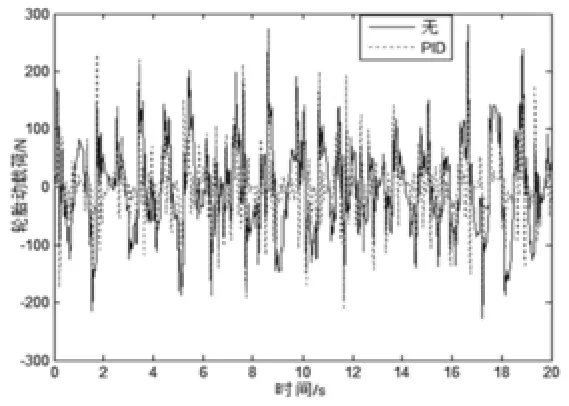
图9 轮胎动载荷仿真曲线

有图8、9、10可以看出，在输入路面激励后，装有PID控制器的空气悬架的汽车车身加速度、悬架动挠度以及轮胎动载荷都发生了变化。其中车身加速度的范围从-0.58—0.62变到了-0.43—0.46，悬架动挠度的范围从-0.012—0.011变为了-0.0125—0.01，轮胎动载荷从-220—280变为了-210—270。综上所述，虽然悬架动挠度和轮胎动载荷变化不是太大，但车身垂直加速度得到有效降低。

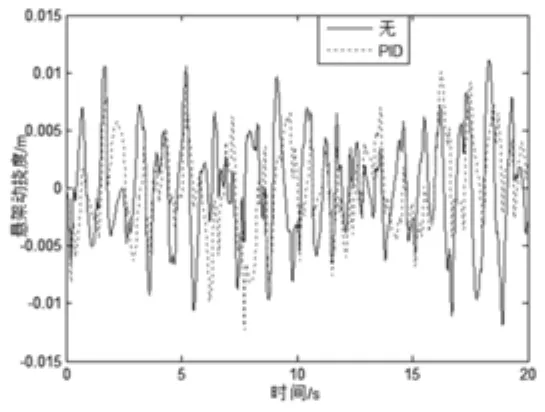
图10 悬架动挠度仿真曲线

5、结论

通过对空气悬架分析，建立了其数学模型，进而搭建有无PID控制的空气悬架系统的仿真模型。对比其仿真曲线结果可以发现悬架的三个指标均有所下降，其中车身垂直加速度的降低较为明显。因此，装有PID控制器的空气悬架不仅可以有效降低其固有振动频率，还可以有效减少悬架在载荷冲击时的变形量，从而降低了车辆在高速行使下对路面的破坏，同时还使其操作稳定性和平顺性有了较为明显的改善，对改善汽车的平顺性有一定的实际意义。

[1] 王望予主编. 汽车设计. 第4版. 北京：机械工业出版社,2004: 192-200.

[2] 刘兴涛.基于ADAMS的膜式空气弹簧动态特性研究[D].2007.05.

[3] 余志生主编.汽车理论.第5版.北京:机械工业出版社,2009: 212-222.

[4] 耿龙伟.空气悬架自整定模糊控制策略及试验研究[D].2014.05.

[5] 蔡颖超.客车空气悬架系统集成及行驶平顺性研究[D].2007.05.

[6] 邱文军.空气悬架力学特性及主动控制策略研究[D].2014.06.

[7] 王正林. MATLAB/SIMULINK与控制系统仿真[M].2005:180-190.

[8] 陈蓉蓉、陈龙. 汽车空气悬架联合型模糊PID控制[J].机械设计与制造.2011.11.

[9] 杜常清、常晓瑞. PID控制策略下主动悬架系统的动态仿真[J].武汉理工大学学报（信息与管理工程版）.2015.12.

The Simulation of Air Suspension System Based On PID Control Strategy

Ma Xiangfei, Li Kai
（Chang'an University, School of Automobile, Shaanxi Xi 'an 710064）

Through the analysis of the air suspension system, establish its mathematical model.Then coupled with the air suspension kinematics equation of two degrees of freedom, built the air suspension system simulation model with PID controller in the MATLAB/SIMULINK.The simulation experiment is conducted under the white noise pavement excitation signal and the experimental results show that air suspension based on PID control strategy can reduce the body vertical acceleration and better increase the ride comfort of vehicles.

Air Suspension; SIMULINK; PID Control

U467.3

A

1671-7988 (2017)08-142-04

马相飞，就读于长安大学。

10.16638/j.cnki.1671-7988.2017.08.049