基于向量式有限元的结构静力分析

胡 强, 曲激婷, 关增伟

(1. 大连理工大学 建设工程学部, 辽宁 大连 116024; 2. 大连理工工程建设监理有限公司, 辽宁 大连 116023)



基于向量式有限元的结构静力分析

胡 强1, 曲激婷1, 关增伟2

(1. 大连理工大学 建设工程学部, 辽宁 大连 116024; 2. 大连理工工程建设监理有限公司, 辽宁 大连 116023)

将位移控制应用到结构静力分析,讨论了影响静力解的主要因素,提出了向量式有限元静力分析的意义.数值分析表明向量式有限元静力分析在大变形、弹塑性和发生屈曲变形的结构中均适用.

向量式有限元; 静力分析; 非线性分析; 大变形; 弹塑性

静力问题是人们在研究结构行为和工程结构设计中经常遇到的基本问题,相对于动力问题而言,静力问题的分析更加简单,分析的结果也更容易被观察和应用.结构的静止状态是结构运动的一种特殊状态,绝对的静止状态实际上并不存在.为了得到静力问题的理论解,以便于在规范和设计过程中应用,传统的静力分析在计算中作了一些简化[1].这些简化限制了结构的载荷和行为,使得静力分析和动力分析被人为地划分为两个不同的范畴,采用两种完全不同的分析思路进行求解[2].这一做法实际上割裂了静力分析与动力分析之间的客观联系,求得的静力解存在一定的局限性.

为了处理各种静力问题,国内外学者已经做了大量研究,提出了各种实用的计算方法[3-4].比较有代表性的有:1960年Clough[5]提出的有限单元法(Finite Element Method),20世纪70年代Cundall[6]提出的离散单元法等,但这些理论的静力分析仍然是属于传统静力分析.

普渡大学丁承先教授等人[7-8],从向量力学的基本概念出发,提出了一种新型数值计算方法----向量式有限元法(Vector Form Intrinsic Finite Element,也称有限质点法).该方法不再以偏微分方程表示结构的行为,而是直接以结构的物理模式对结构的行为进行描述;线性和非线性、连续行为和不连续行为以及静力问题和动力问题均采用统一的计算格式,使得结构复杂行为的分析难度大大降低.向量式有限元静力分析摒弃了传统静力分析中对结构行为的限制,将静力分析与动力分析统一在了一起,是一个广义的分析.

向量式有限元的研究和应用目前还处于起步阶段,但已经在多个领域取得了研究成果.张燕如[9]应用向量式有限元研究了单跨门式刚架在真实火灾下载荷和约束条件对结构性能的影响;王仁佐等[10]利用向量式有限元对桁架结构弹塑性和断裂过程进行了模拟;陈柏宏[11]运用向量式有限元对隔振桥梁在强震条件下的极限状态进行了研究.在静力分析方面,朱明亮等[12]将向量式有限元应用于索穹顶的静力分析,在ANSYS分析已不收敛情况下向量式有限元仍然能够得出准确结果;喻莹等[2]对结构进行动力非线性分析并阐述了向量式有限元“静”与“动”问题分析的特殊思路.静力分析的内容在文献中均有涉及,但专门就这一问题进行介绍和深入思考的文献还比较少.

本文将就向量式有限元结构静力分析的特点和思想进行专门地研究,并就其应用作一些有益的探讨,最后通过数值算例验证向量式有限元静力分析的有效性.

1 向量式有限元简介

向量式有限元是结构行为分析的新方法,该方法创新性地提出了点值描述、途径单元和虚拟逆向运动的概念.点值描述,即在时间上将结构离散为一群质点,用质点的运动来描述结构的几何形状和空间位置的变化,质点之间采用无质量的结构单元连接和传递内力,质点的运动满足牛顿第二定律.途径单元,即在空间上将运动历程分割为一系列单元,在途径单元内结构单元的变形为小变形,可以有大变位;结构单元的特性、组合方式以及质点的受力的改变等不连续行为只发生在途径单元之间,而在途径单元内保持不变.虚拟逆向运动,即采用虚拟的逆向运动将结构单元的刚体位移从变形中直接扣除,得到计算内力增量所需的纯变形;计算内力增量,再将内力增量叠加得到的内力全量经过一个虚拟的正向运动回归到当前位置,得到当前时刻的内力.

结构中质点的运动方程[1]可写成

(1)

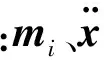
(2)

将式(2)代入式(1),当作用在结构上的外力已知,观察结构的响应时可采用力控制(force controlled)方法,即

(3)

当结构位移已知,观察作用在结构上的外力和结构内力时可以使用位移控制(displacement controlled)方法,即

(4)

式中下角标0、n-1、n和n+1分别表示初始、n-1、n和n+1时间步,h为时间步长.

从上面的计算公式推导过程可以看到,结构的运动控制方程是一组向量方程式,每个质点单独进行求解,其求解过程中只需进行一系列简单的向量运算,不形成总刚度矩阵,避免了有限单元法中整体刚度矩阵求逆带来的运算量剧增和复杂的迭代运算,且计算效率不受质点编号顺序的影响.限于篇幅,向量式有限元的详细计算流程可参考文献[1,13],这里不再赘述,本文重点讨论向量式有限元分析静力问题的特点和思想.

2 向量式有限元静力分析的基本思想

向量式有限元以牛顿第二定律作为控制方程,计算结果是结构的动力响应,因此,结构动力分析是向量式有限元分析的本质.为了得到结构的静力解,向量式有限元采用缓慢加载和设置阻尼两种方法来逼近结构的静止状态[14].

缓慢加载与静力试验中逐级加载的思路一致,即在单位时间步长内,施加很小的力增量或位移增量,以免改变结构的运动趋势.缓慢加载虽不能削减加载过程引起的结构动力反应,但较小的加载速度能够将结构的振动限制在一定的范围内,有利于进一步通过阻尼耗散结构动能.如图1所示,采用力控制或位移控制时,可先经过一个斜坡缓慢地将载荷或位移分别加到指定位置,再稳定一段时间,其中t0和ET分别是缓慢加载时间和总加载时间.同一加载过程中,t0和ET比值越大加载速度就越缓慢.

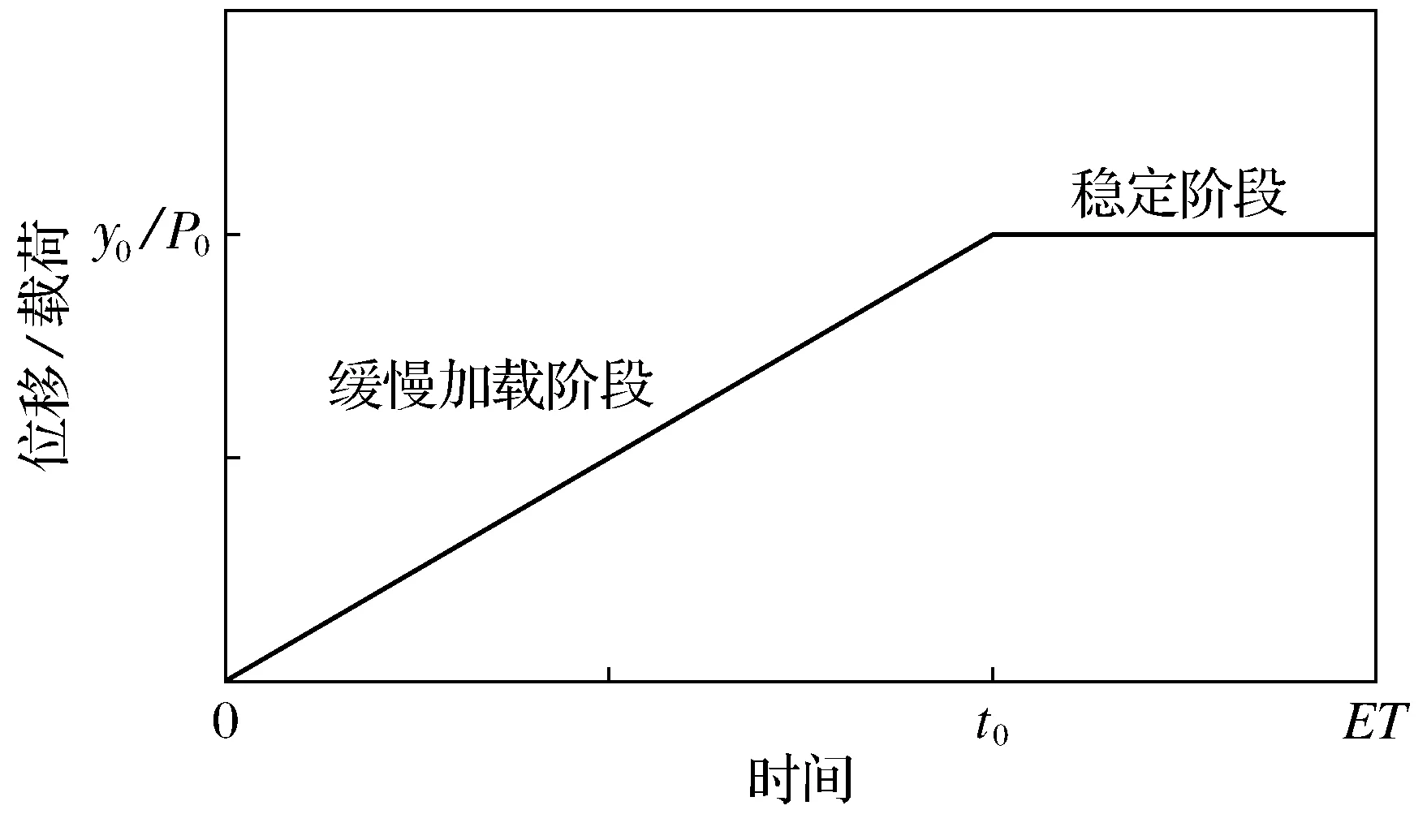
图1 位移控制法或力控制法的加载过程

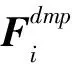
(5)

式中,μ是阻尼系数,可任取一个正数值,不必按结构的真实模型选取.

向量式有限元静力分析方法是一种静力逼近算法,不能获得结构绝对的静止状态,因此,需要设置合适的收敛准则来结束计算.对于力控制和位移控制可分别采用式(6)和式(7)作为收敛准则[13]

(6)

(7)

式中εx和εf分别为给定的位移和力的收敛精度,一般取值非常小(10-10～10-5),具体取值根据计算精度和计算时间综合考虑.

传统的静力分析作了两个假设[1]:路径独立和静态解.①静力分析时,仅需考虑初始和终止两个状态,不考虑中间的转变过程,即不论中间过程外力如何施加、阻尼如何耗能、结构的形状和位置如何改变,只要最终的边界条件和外力相同,结构都会达到相同的终止状态;②忽略惯性项,认为控制方程是平衡方程,即认为初始和终止状态是两个绝对静止平衡态.

向量式有限元静力分析没有以上两点假设的限制,是一种广义的分析,除了需要计算初始和终止状态的外力和位移外,还需要计算中间过程的外力和位置变化,需要更多的已知条件,同时也可得到更多的结果,这是向量式有限元静力分析的特点.因此,采用向量式有限元得到的静力解,与传统静力分析中先经过一系列简化再通过平衡方程的得到的静力解可能很接近,但不会完全相同.

3 数值算例

3.1 力控制法

以一个平面桁架[15]为例(如图2所示),各杆件截面面积均为2.5×10-3m2,弹性模量E=210 GPa,密度ρ=7.8×103kg/m3,A点受到一个竖直向下的集中载荷P=20 MN.采用向量式有限元方法对该平面桁架进行静力分析.

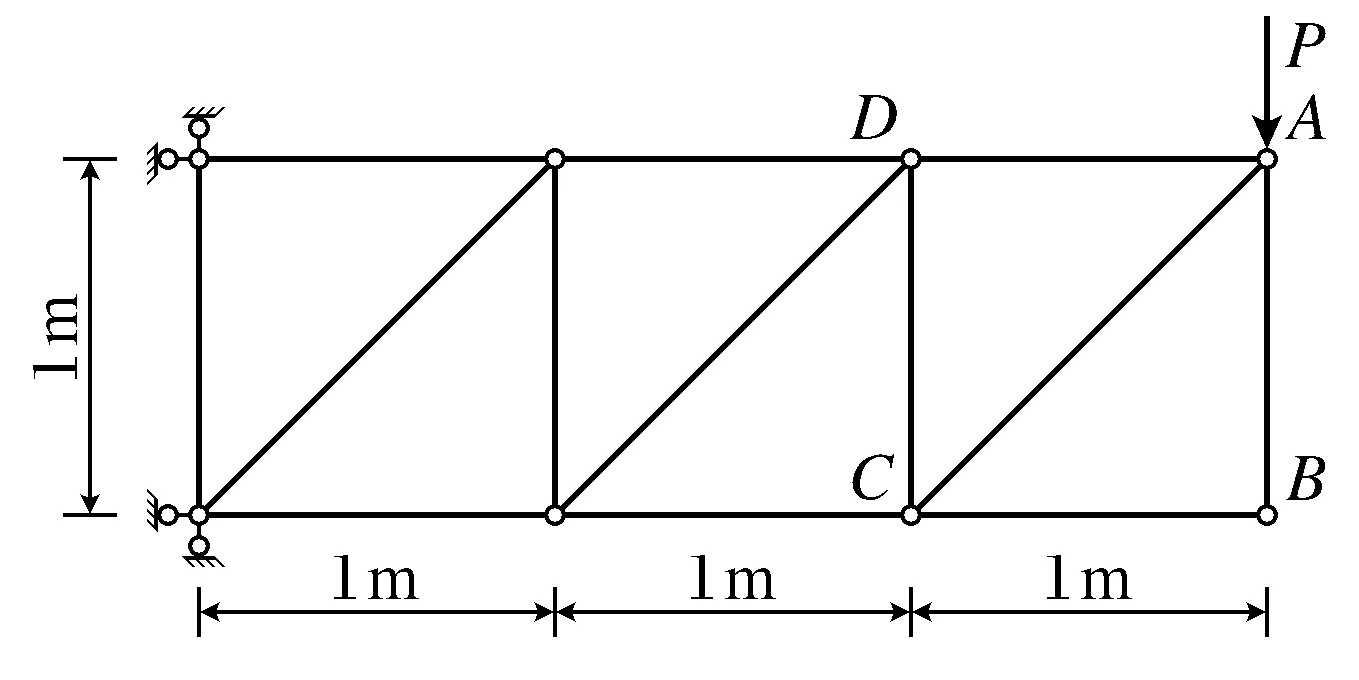
图2 平面桁架单元模型

取时间步长h=1.0×10-4s,分析时长为0.3 s,阻尼系数μ=50.将A点所受外力P逐步缓慢地施加到结构上,0～0.15 s为缓慢加载阶段,0.15～0.30 s为稳定阶段.经过缓慢加载阶段,结构从初始平衡状态过渡到外力P作用下的平衡状态,稳定阶段结束后,A点竖向位移为向下的1.124 m,整个加载过程中A点位移的变化如图3所示.

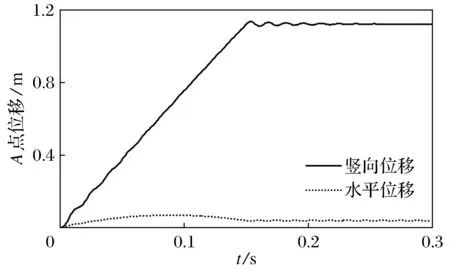
图3 平面桁架A点在力加载下的位移

(1) 向量式有限元与有限单元法分析结果比较.采用SAP 2000对该平面桁架进行静力分析,计算结果如图4所示.A点竖向位移为向下的1.103 5 m,与向量式有限元计算结果相差约为1.9%,说明了本文方法的合理性.A点竖向位移与杆件初始长度处于同一数量级,说明该桁架在集中载荷P的作用下已经出现了大变形,该问题是一个典型的几何非线性问题,小变形假设已不再适用.

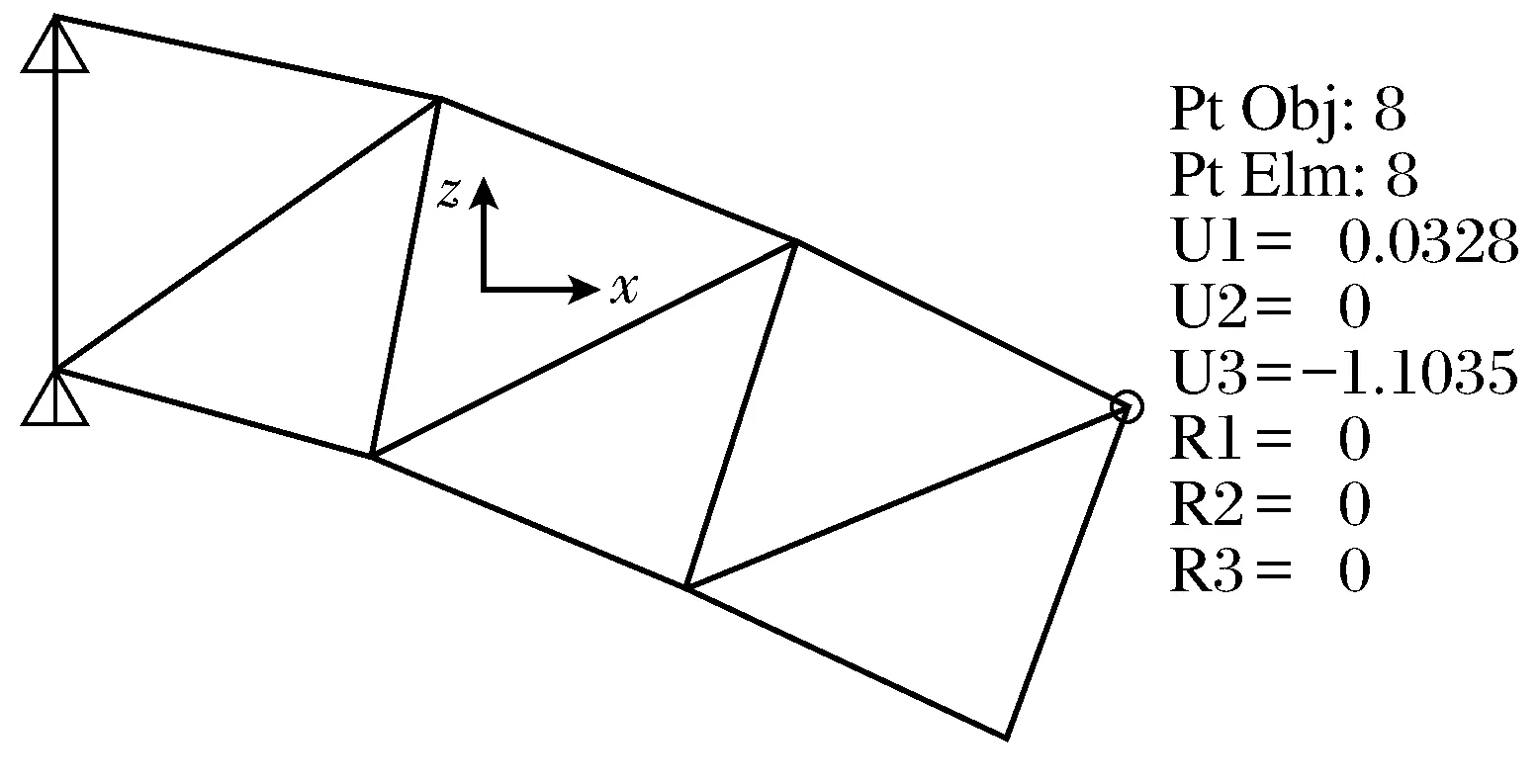
图4 SAP2000分析结果

(2) 加载速度和阻尼的影响.当缓慢加载时间统一取为0.01 s时,A点的竖向位移变化如图5所示,当阻尼系数不是很大(例如μ=50和μ=100)时,结构处于低阻尼状态,A点位移在1.124 m附近振荡后趋于稳定,且阻尼取值越大就能够越快地稳定;当阻尼系数很大(本文取为μ=2×104)时,结构处于超阻尼状态,A点位移无振荡地趋近平衡位置1.124 m处,但所需时间明显更长.

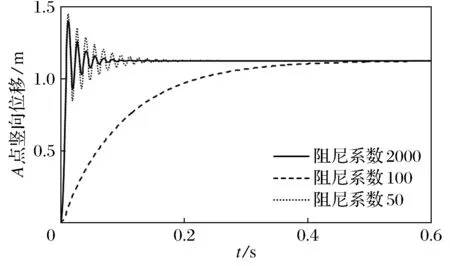
图5 阻尼的影响

因此,当阻尼系数取非零值且不是很大时,阻尼系数取值越大,结构的动力反应就能够越快地被削弱,但阻尼系数取值过大虽然能够限制结构振荡,但同时也延迟了结构反应到达平衡位置的时间,反而降低了取得稳定静力解的效率.在向量式有限元的静力分析中,加载速度和阻尼系数是两个重要的影响因素.分别考虑加载速度和阻尼的影响,将加载时间和阻尼系数设为表1所示的值,其中t0(s)越大表示加载速度越缓慢.由图6可见,阻尼一定的情况下,加载越缓慢,稳定阶段结构位移的波动越小,动力反应越小;不同的加载速度,中间过程结构的运动趋势是不同的.

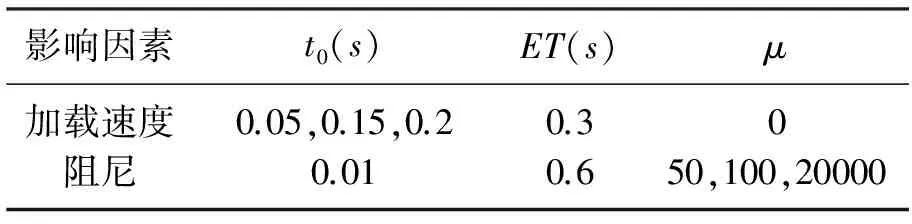
表1 加载速度和阻尼系数

向量式有限元静力分析中,不同的阻尼系数相当于不同的耗能机制,不同的阻尼系数取值得到的分析结果几乎相同,但计算的效率有较大差异.

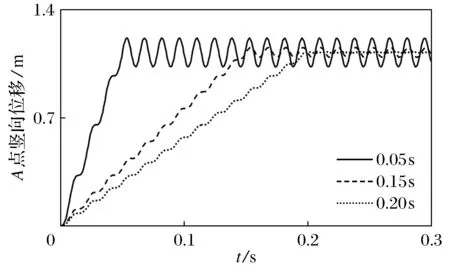
图6 加载速度的影响

3.2 位移控制法

图7所示为一个由24根杆件铰接而成的经典的空间桁架穹顶[16],杆件截面面积S=20×10-6m2,密度ρ=6.309×103kg/m3.采用双线形强化模型分析该桁架模型的弹塑性大变形行为,弹性模量E=3.03 kPa,强化段Et=0.2 GPa,屈服极限σy=0.25 GPa.穹顶A点上受到一个集中载荷P作用.

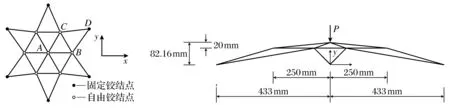
图7 空间星型穹顶

本文提出向量式有限元静力分析除使用力控制法外,还可使用位移控制法.采用向量式有限元位移控制方法计算载荷的P大小,时间步长取h=5.0×10-4s,阻尼系数μ=50.位移施加过程:从0～0.2 s缓慢地将70 mm的竖向位移施加到结构的A点,再稳定一段时间(0.2～0.4 s).

计算得到AB、BC和CD杆的轴力时程如图8所示,从图中可以看出,AB杆和BC杆分别在t=0.016 s、t=0.163 s达到屈服轴力-5 000 N,表明结构此时已经进入弹塑性状态,因此是一个材料几何双重非线性问题;t=0.014 s时,A竖向位移达到47.57 mm,三杆轴力突然变号,该桁架发生屈曲变形;t=0.2 s后,经过些许振荡,AB、BC和CD杆轴力最终分别稳定在2 962 N、-4 980 N和-1 730 N.在分析的过程中,向量式有限元不仅计算了最终结果,还计算了中间过程(稳定前的分析部分);阻尼取值较大,加载速度设置地较小,结构振动很小,接近静态,中间过程能够很好地反映轴力的变化,具有一定的价值,向量式有限元静力分析可计算中间过程的优势得到了体现.

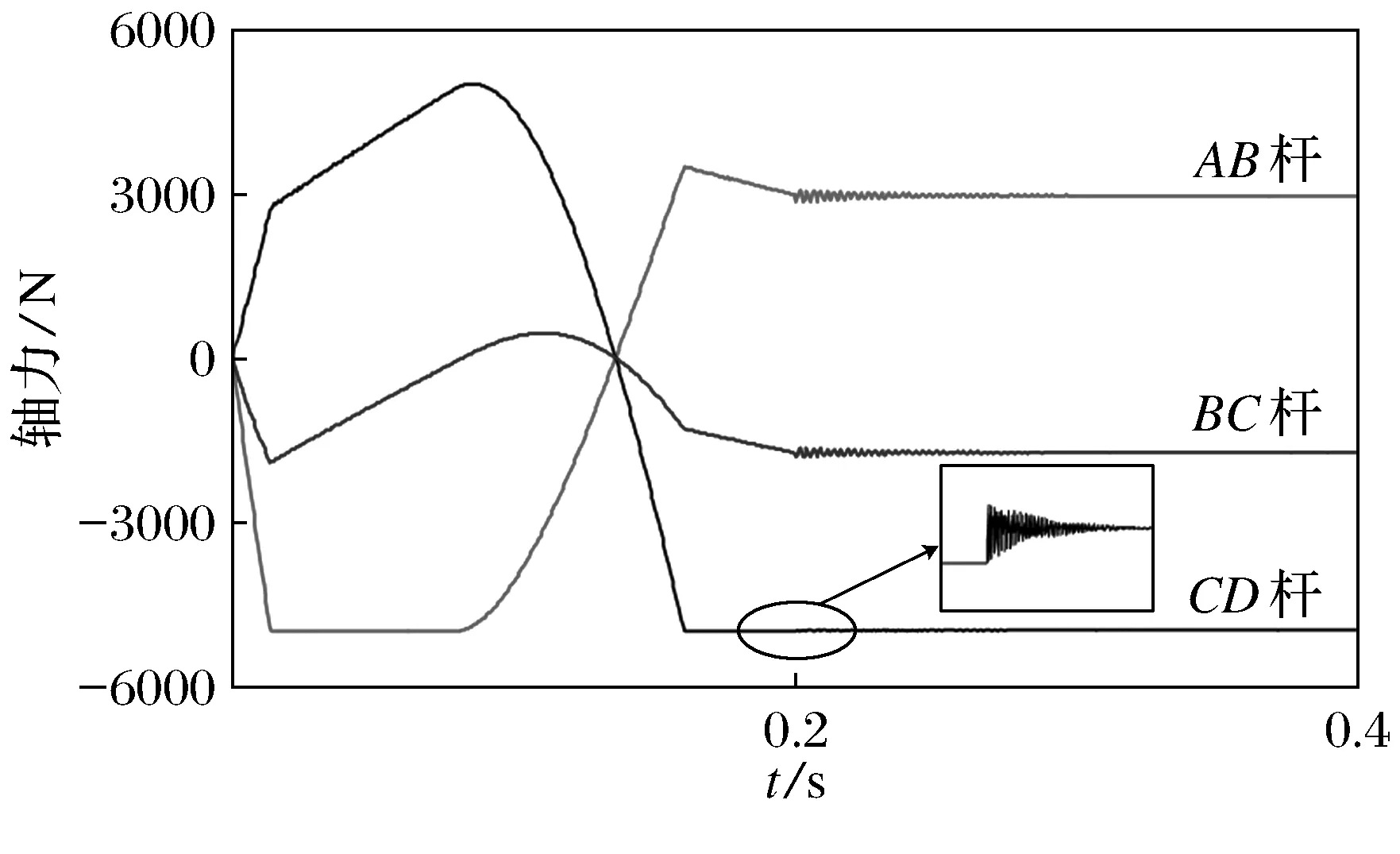
图8 AB、BC和CD杆轴力变化过程

位移施加过程:从0～0.4 s缓慢地将80 mm的竖向位移施加到结构的A点,稳定时间取为0 s.A点竖向位移与外载荷关系曲线如图9所示,对比文献[16]中Driemeier的分析结果,可以看到向量式有限元静力分析的结果与文献吻合得较好,验证了本文基于向量式有限元静力分析方法的正确性.同时,图9中还给出了线弹性的分析结果,实际上该曲线(线弹性和弹塑性曲线)即是研究结构屈曲行为时经常讨论的载荷-位移平衡曲线.有限单元法中计算该曲线的过程是一个较为复杂的过程,不仅需要复杂的迭代,还需要在极值点附近人为地加入一些特殊处理;而对于向量式有限元来说,该曲线只是静力分析的中间过程曲线,仅需通过在全过程缓慢加载和适当设置阻尼取值便自动追踪到了结构的屈曲后行为,期间不需要对极值点作任何不同于曲线其他部分的特殊处理.这可以看作是向量式有限元静力分析的一个应用.

图9 A点施加不同竖向位移对应的外载荷

4 结 论

向量式有限元理论打破了静力分析与动力分析的界限,不仅计算最终状态,还可以得到计算的中间过程,是一个广义的分析.本文介绍了向量式有限元静力分析的基本思想和特点,指出了向量式有限元静力分析与传统静力分析的区别,通过两个数值算例分别从力控制法和位移控制法两个方向对结构进行静力分析.结果表明:

(1) 阻尼系数和加载速度是影响向量式有限元静力分析的两个重要因素,缓慢加载和较大的阻尼系数有助于结构反应尽快地稳定于平衡位置.

(2) 适当地设置阻尼取值并控制加载速度,使静力求解的中间过程与结构受力后的实际情形接近,可得到结构内力和变形时程,也可追踪结构的屈曲变形行为,此时中间过程也具有了一定的工程意义.

(3) 结构处于欠阻尼和超阻尼状态均不能使结构尽快收敛于静力解.建议在向量式有限元静力分析的基础上,进一步推导临界阻尼作为阻尼系数,可以减少计算中间过程时间步数,提高向量式有限元静力分析的效率.

(4) 基于向量式有限元的静力分析不仅可采用力控制法也可采用位移控制法,该方法在分析大变形、弹塑性、屈曲变形等复杂结构行为时均适用.向量式有限元静力分析具有广泛的应用前景.

[ 1 ] 丁承先,段元锋,吴东岳. 向量式结构力学[M]. 北京:科学出版社, 2015. (DING C X, DUAN Y F, WU D Y. Vector mechanics of structures[M]. Beijing: Science Press, 2015.)

[ 2 ] 喻莹,许贤,罗尧志. 基于有限质点法的结构动力非线性行为分析[J]. 工程力学, 2012,29(6):63-69. (YU Y, XU X, LUO Y Z. Dynamic nonlinear analysis of structures based on the finite particle method[J]. Engineering Mechanics, 2012,29(6):63-69.)

[ 3 ] 束忠文,曲激婷. 对拟力法理论中塑性弯矩和动力方程的分析与讨论[J]. 沈阳大学学报(自然科学版), 2016,28(2):155-159. (SHU Z W,QU J T. Analysis and discussion on plastic analogy method moment and equations of force analogy method[J]. Journal of Shenyang University(Natural Science), 2016,28(2):155-159.)

[ 4 ] SHU Y, QU J T. Estimation of structure plastic energy based on equivalent sd of system using force analogy method[J]. Journal of Shenyang University(Natural Science), 2015,27(5):415-419.

[ 5 ] CLOUGH R W. The finite element method in Plane stress analysis[C]. Proceedings of 2nd ASCE Conference on Electronic Computation, Pittsburgh, Paris, 1960.

[ 6 ] CUNDALL P A. A computer model for simulating progressive large scale movement in blocky rock system[J]. Proceedings of the Symposium of the International Society of Rock Mechanics, 1971,2:129-136.

[ 7 ] EDWARD C T, CHIANG S,YEON K W. Fundamentals of a vector form intrinsic finite element:PartⅠ.Basic procedure and a plane frame element[J]. Journal of Mechanics, 2004,20(2):113-122.

[ 8 ] EDWARD C T, CHIANG S, YEON K W .Fundamentals of a vector form intrinsic finite element:PartⅡ.Plane solid elements[J]. Journal of Mechanics, 2004,20(2):123-132.

[ 9 ] 张燕如. 钢结构火害之向量式有限元素法分析[D]. 台南:成功大学, 2007. (ZHANG Y R, Vector form intrinsic finite element analysis of steel structures at fire environment[D]. Tainan: Cheng Kung University, 2007.)

[10] 王仁佐,庄清锵,关东岳,等. 向量式空间桁架弹塑性大变形分析[J]. 中国土木水利工程学刊, 2004,17(4):633-646. (WANG R Z, ZHUANG C C, WU D,Y, et al. Plastic large deformation analysis of space truss in vector form intrinsic finite element[J]. Journal of the Chinese Institute of Civil & Hydraulic Engineering, 2004,17(4):633-646.)

[11] 陈柏宏. 运用向量有限元素法于隔震桥梁之非线性动力分析[D]. 桃园:“中央”大学, 2008. (CHEN B H. Nonlinear dynamic analysis of isolated bridges by VFIFE[D]. Taoyuan: “Central” University, 2008.)

[12] 朱明亮,董石麟. 向量式有限元在索穹顶静力分析中的应用[J]. 工程力学, 2012,29(8):236-242. (ZHU M L, DONG S L. Application of vector form intrinsic finite element method to static analysis of cable domes[J]. Engineering Mechanics, 2012,29(8):236-242.)

[13] 杨超. 薄膜结构的有限质点法计算理论与应用研究[D]. 杭州:浙江大学, 2015. (YANG C. Research on computational theory and applications of finite particle method for membrane structures[D]. Hangzhou: Zhejiang University, 2015.)

[14] 王震,赵阳,杨学林. 平面薄膜结构屈曲行为的向量式有限元分析[J]. 浙江大学学报(工学版), 2015,49(6):1116-1122. (WANG Z, ZHAO Y, YANG X L. Analysis of buckling behavior of planar membrane structures based on vector form intrinsic finite element[J]. Journal of Zhejiang University (Engineering Science), 2015,49(6):1116-1122.)

[15] SLAATS P M A, DE J J, SAUREN A. Model reduction tools for nonlinear structural dynamics[J]. Computers &Structures, 1995,54(6):1155-1171.

[16] DRIEMEIER L, PROENCA S P B, ALVES M. A contribution to the numerical nonlinear analysis of three-dimensional truss systems considering large strains, damage and plasticity[J]. Communications in Nonlinear Science and Numerical Simulation, 2005,10(5):515-535.

【责任编辑: 肖景魁】

Static Analysis of Structures Based on Vector Form Intrinsic Finite Element Method

HuQiang1,QuJiting1,GuanZengwei2

(1. Faculty of Infrastructure Engineering, Dalian University of Technology, Dalian 116024, China; 2. Dalian University of Technology Project Management CO., LTD, Dalian 116023, China)

The displacement control method is applied to static analysis of structures. The main factors that affect the static analysis are discussed. The significance of vector finite element analysis is proposed. The numerical analysis shows that this method is suitable for a structure with large deformation, elastic or plastic deformation.

vector form intrinsic finite element; static analysis; nonlinear analysis; large deformation; elastic-plastic

2016-12-07

国家重点研发计划资助项目(2016YFC0701108).

胡 强(1989-),男,四川眉山人,大连理工大学硕士研究生.

2095-5456(2017)02-0158-06

TU 312

A