从变换中寻找二元最值问题的不变性

☉江苏省苏州市第四中学 校蒋艳

从变换中寻找二元最值问题的不变性

☉江苏省苏州市第四中学 校蒋艳

一、问题背景

二元最值是中学数学中的难点问题，其相比一元最值来说，因为变量的增加使得最值的求解难度大幅度上升.从教学经验来看，学生对于单变量最值的求解能掌握基本方法，但是对于二元多变量问题的处理往往缺乏头绪，无法辨别其入手的角度、方向.

从知识背景来说，对高中数学教材进行大量的研究与教学实践发现，二元最值问题涉及的知识点广，包括函数、向量、三角函数、线性规划、立体几何、解析几何等等；在解决方法上，有代数式的变形变换、构造法、换元法等；就数学思想上，有分类讨论、数形结合等基本数学思想.另一方面来说，二元最值问题正因为比较分散，也没有完全可以套用的共性模型.这是本问题之所以成为难点的原因.

二、学习困惑

在教育改革不断深化推进中，数学课程的编排难度递进和知识结构呈现螺旋式上升的形式.但是二元最值问题依旧是学生感到困难与难以把握的内容，造成这种现象的原因有以下几个方面：

1.缺乏统一的解题方法

学生最理想的学习过程是掌握一种方法解决一类问题，但是二元最值问题没有“一招鲜”，根据实际问题派生出多种解法、多重视角、多维思考，复杂性强，要求学生考虑的方面比较多，思维量就比较大.如果某一个方面没有考虑到的话，可能都造成错误的解法，或者考虑的方向不正确，也会造成错误.

2.问题涉及的知识面较广

二元最值问题包括函数、向量、三角函数、线性规划、立体几何、解析几何等等，尤其是需要对问题进行高技术含量的转化与化归，综合性强，学生很难根据自己已有的经验来解决此类问题.

3.数学思维能力要求较高

由于学生的思维发展水平不同，认知的结构和水平、理解能力、心理发展特点有明确的差异性特征，所以对最值问题学习对象的特点快速、全面、正确的把握，是能否解决好最值问题的一个必备条件.因此学生在处理二元最值问题的时候，自身的知识储备：知识模块之间横向联系，相关知识之间的纵向联系，编织成一个知识网络，对学生的思维能力与思维品质都提出了非常高的要求.

三、寻找不变性策略

二元最值问题是指含有多个变量的最大值、最小值或取值范围的求解问题，此类问题涉及的知识广、难度大、方法多、灵活多变、综合性较强成为最值求解中的难点与热点.其具体的解题策略受题设条件以及目标式的结构与形式影响最大.

二元最值问题是指含有多个变量的最值问题，数学表达式的结构会对学生形成一定的视觉冲击.所以解题首先应该调整题设条件与目标式的结构，具体策略如下：

1.消元换元策略

数学是美的，数学是简洁的.此类问题的解题的核心策略首先应当是减少未知量——消元.多元最值往往涉及两元以上，通过题设的等式条件将多元降解为单元，从而形成能求解的模式.

问题1设x，y为实数，若4x2+y2+xy=1，则2x+y的最大值是_______.

分析1：题设条件是一个有关x，y的二元二次方程，目标式是有关x，y的一次式，因此可令2x+y=t，代入4x2+ y2+xy=1消元，得到t为参数，有关x的一元二次方程有解.

解法1：设2x+y=t，则y=t-2x代入4x2+y2+xy=1得到

6x2-3tx+t2-1=0.

分析2：因为2x+y是平面二维问题，两个变量x，y之间应该存在一定的线性关系，所以我们在解决此类问题的时候可以先建立x，y线性关系，实现代入消元.

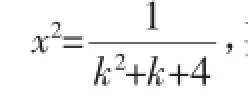
当且仅当k=2时，等号成立.

此法在多元最值问题解决中消元的效果很好，所以鼓励学生要大胆去尝试和运用.

2.几何视角策略

中学数学中的两元最值问题，往往有几何视角.继续观察问题1，我们发现：4x2+y2+xy=1类似于标准的椭圆方程，因此可以猜测其是标准椭圆旋转后的方程，而求2x+y的最大值从几何视角解释不正是直线截距的最大值嘛！因此可以从这样的通性入手：

说明：消元换元是针对二元最值问题最基本的解决思路，尽管问题可能千变万化，但是从问题解决中获得的基本思路是不变的，消元正是将复杂问题简单化的典型.另一方面，中学数学二元最值问题还有几何的视角，这是教学必须渗透的，因为几何视角往往降低了二元最值问题的代数难度，从而形成了较为简单的解题思路.

问题2若实数x，y满足x2+y2≤1，则F=|2x+y-2|+|6-x-3y|的最小值为__________.

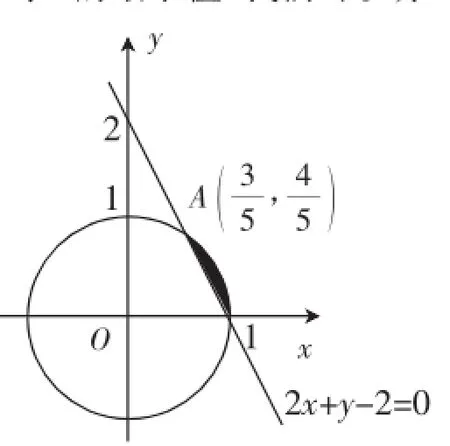
图1

解析：求解本题的难点是如何去掉绝对值符号，首先我们发现当x2+y2≤1时，6-x-3y≥0，所以|2x+y-2|+|6-x-3y|=|2x+y-2|+6-x-3y，为了求F的最小值，我们可以分为两类：2x+y-2＞0与2x+ y-2≤0，把问题转化为约束条件（x2+y2≤1及2x+y-2＞0或2x+y-2≤0）下，求F的最小值.

如图1，直线l：2x+y-2=0将单位圆面x2+y2≤1分为两部分：

（1）当2x+y-2＞0时，F=|2x+y-2|+|6-x-3y|=x-2y+4，即问题转化为求目标函数z=x-2y+4在阴影区域及其边界的最小值，由线性规划知识可求得F＞3.

说明：这种解法的最初想法在于去掉绝对值，而这是碰到绝对值问题时最容易想到的一种思考方法，思路比较自然.本题二元最值问题转换为几何视角，是从条件x2+y2≤1入手思考，从而以基本的分类讨论进行求解.

3.不等式视角策略

二元最值问题也可以从不等式视角切入，这是纯粹代数的解决方式.从解决过程来看，能用不等式解决的问题往往来得比上述消元、几何策略都更简单，但思维含量比较高.但从大量的问题中，我们发现还是需要掌握下列重要的不等式结论：

结论1完全平方式a2+b2≥2ab，a2+b2≥-2ab（a，b∈R）.

结论3二维柯西不等式（x2+y2）（a2+b2）≥（ax+by）2，变量范围：x，y，a，b∈R，等号成立的条件：bx-ay=0.

最值问题尤其是含绝对值的最值问题通常可以借助绝对值不等式、柯西不等式等重要不等式的性质进行求解.在求解时，要注意取到最值时的条件.对于任意实数a，b，|a|+|b|≥|a+b|，当且仅当ab≥0取等号；|a|+|b|≥|ab|，当且仅当ab≤0取等号.因此，继续研究问题2我们有：

当x2+y2≤1时，易知6-x-3y＞0.由于x2+y2≤1，不妨令x=rcosθ，y=rsinθ，其中0≤r≤1，0≤θ≤2π.

（1）当2x+y-2＞0时，

F=|2x+y-2|+|6-x-3y|≥|（2x+y-2）+（6-x-3y）|=|x-2y+ 4|.①

（2）当2x+y-2≤0时，F=|2x+y-2|+|6-x-3y|≥|（2x+y-2）-（6-x-3y）|=|3x+4y-8|.②

说明：利用绝对值不等式减少绝对值个数也是解决此类问题时的一种常规方法，在选用|a|+|b|≥|a+b|还是需要分别讨论，此外还要注意使用绝对值不等式时的取等号条件.在求解①与②的最小值时，由x2+y2≤1的条件进行三角代换，是非常自然的思路，但求解时易忽视对“2x+y-2＞0时”F＞3的证明.

总之，二元最值问题的解决往往涉及多个知识，因此没有一成不变的初等方法.但是从上述列举的典型案例中，我们不难发现其依旧有不变性可以总结——消元策略、几何视角策略、不等式策略，相对而言这三种策略是解决二元最值最为常用的策略.教学中教师要多加以合理引导，让学生通过尝试获得更为优秀的解题体验，从而加强二元最值问题解决的信心，从高效的学习方法获得问题解决的快乐.

1.叶燕.多元变量的最值探讨［J］.中学数学（上），2013（11）.

2.石磊.例谈多元最值问题的不等式解法［J］.数理化学习，2013（12）.

3.邓城.一道多元变量最值问题的探讨过程与反思［J］.福建中学数学，2011（11）.