例谈函数不等式证明的若干策略

☉江苏省丹阳市吕叔湘中学 张 鹏

例谈函数不等式证明的若干策略

☉江苏省丹阳市吕叔湘中学 张 鹏

利用导数研究函数的性质，再用性质来证明不等式是函数、导数、不等式综合问题中的一个难点，也是近几年高考的热点问题.这类问题往往难度较大，解题方法灵活多变，对学生的思维能力要求较高，如何利用导数证明不等式？本文针对几类常见不等式类型谈谈处理的一些方法.

一、构造函数证明不等式

有些不等式的证明问题，形式较为复杂，常让人感到无从下手，很难找到切入点，这时，我们不妨变换一下思维角度，从所证不等式的结构和特点出发，结合已有知识，构造函数，再借助导数的知识实现问题的转化，从而证明不等式成立.

例1已知函数g（x）=lnx+ax2+bx，函数g（x）的图像在点（1，g（1））处的切线平行于x轴.

（1）用a表示b；

（2）试讨论函数g（x）的单调性；

解：（1）（2）具体解答略.

（3）分析：此不等式右端不妨视为一个数列｛an｝（an≥0，n∈N*）的前n项和，若将左端也视为一个正项数列｛bn｝的前n项和Sn，那么要证这个复杂的不等式，就只需证bn＞an（n∈N*），从而寻求出解题方向.

因为Sn=ln（n+1），所以当n≥2时，Sn-1=lnn.

当n=1时，b1=S1=ln2满足上式，

要证原不等式成立，

故只需证lnx+x2-3x＞-2，x＞1.

由（2）知，当a=1时，函数g（x）=lnx+x2-3x在（1，+∞）上单调递增，

则g（x）=lnx+x2-3x＞g（1）=-2.

故lnx+x2-3x＞-2在x∈（1，+∞）上成立.

故问题得证.

证明：由（2）知，当a=1时，函数g（x）=lnx+x2-3x在（1，+∞）上单调递增，

则g（x）=lnx+x2-3x＞g（1）=-2，即lnx＞-x2+3x-2，x＞1.

（1）若（fx）无极值点，求a的取值范围；

（2）设g（x）=x+1-（lnx）a，当a取（1）中的最大值时，x求g（x）的最小值；

解：（1）（2）（具体过程略）.

（3）分析：类似上面那个例题中不等式的证明思路，不妨将此不等式左端视为一个数列｛an｝（an≥0，n∈N*）的前n项和，若将右端也视为一个正项数列｛bn｝的前n项和Sn，那么要证这个复杂的不等式，就只需证an＞bn（n∈N*），从而寻求出解题方向.

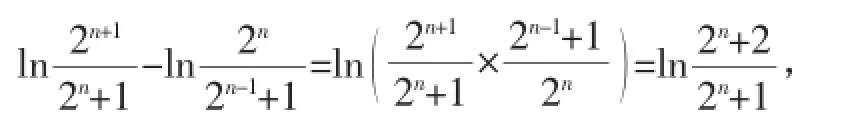
要证原不等式成立，

故结论成立.

评注：构造函数用导数证明不等式，其步骤一般是：构造可导函数，研究函数的性质（如函数的单调性、极值、最值），利用性质得出不等关系，最后整理得出结论.因此，如何根据不等式的结构特征构造一个可导函数是用导数证明不等式的关键.

二、利用函数F（x）=f（x）-g（x）的最值证明

例3已知函数f（x）=nx-xn，x∈R，其中n∈N*，n≥2.

（1）讨论f（x）的单调性；

（2）设曲线y=f（x）与x轴正半轴的交点为P，曲线在点P处的切线方程为y=g（x），求证：对于任意的正实数x，都有f（x）≤g（x）；

（3）若关于x的方程f（x）=a（a为实数）有两个正实根

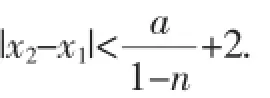
解：（1）（3）略.

（2）证明：设点P的坐标为（x0，0），n-n2，曲线y=（fx）在点P处的切线方程为y=f′（x0）（x-x0），即g（x）=f（′x）0（x-x0）.

令F（x）=f（x）-g（x），即F（x）=f（x）-f′（x0）（x-x0），

则F′（x）=f′（x）-f′（x0）.

由于f′（x）=-nxn-1+n在（0，+∞）上单调递减，故F′（x）在（0，+∞）上单调递减.又因为F′（x0）=0，所以当x∈（0，x0）时，F′（x0）＞0，当x∈（x0，+∞）时，F′（x0）＜0.所以F（x）在（0，x0）上单调递增，在（x0，+∞）上单调递减，所以对任意的正实数x都有F（x）≤F（x0）=0，即对任意的正实数x，都有f（x）≤g（x）.

评注：本题第（2）问利用了构造函数证明不等式这一重要思想方法，体现数学中的构造法在解题中的重要作用.

例4已知函数f（x）=（1+x）e-2x.当x∈［0，1］时，求证：

证明：（1）要证x∈［0，1］时，（1+x）e-2x≥1-x，只需证（1+x）e-x≥（1-x）ex.

记h（x）=（1+x）e-x-（1-x）ex，

则h′（x）=［（1+x）e-x-（1-x）ex］′=x（ex-e-x）.

当x∈（0，1）时，h′（x）=x（ex-e-x）＞0，因此h（x）=（1+ x）e-x-（1-x）ex在［0，1］上为增函数，故h（x）≥h（0）=0.

所以（1+x）e-2x≥1-x，x∈［0，1］.

只需证ex≥1+x.

记k（x）=ex-x-1，

则k′（x）=ex-1，当x∈（0，1）时，k′（x）=ex-1＞0，因此k（x）=ex-x-1在［0，1］上为增函数，故k（x）≥k（0）=0.

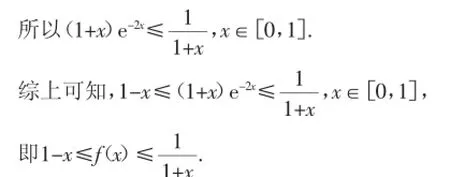
三、利用f（x）min＞g（x）max证明

（1）求a，b；

（2）证明：f（x）＞1.

解：（1）a=1，b=2.（过程略）

（2）证明：由（1）知

所以当x∈（0，1）时，h′（x）＞0；当x∈（1，+∞）时，h（′x）＜0.

故h（x）在（0，1）上单调递增，在（1，+∞）上单调递减，从而h（x）在（0，+∞）上的最大值为，即h（x）当且仅当x=1时取等号）.

评注：本题在证明（fx）＞1时，学生会想到直接求出（fx）的最小值，再证明（fx）min＞1，或构造函数F（x）=（fx）-1，再证明F（x）min＞0.但无论哪种方法在函数求导之后，其导函数的零点都不方便求出，从而导致思维受阻，如果我们注意到这两种思路受阻是由exlnx这个因式引起的，那么我们就可以尝试将exlnx进行分离，将欲证不等式转化成，然后再加强为g（x）min＞h（x）max进行证明，从而得到上面的证法.关于这种方法的运用，还可以参考2012年山东高考理科第22题.

四、利用放缩法证明

上述两种方法是处理导数中不等式证明问题的基本方法，无论是哪种方法，我们都希望变形之后的函数的性态是比较清楚的.但有些题目，在对函数进行变形后，其性态依然难以确定，这时我们就需要用放缩法对原函数或导函数进行放缩，使得问题能够顺利求解.

例6已知函数f（x）=ex-ln（x+m）.

（1）设x=0是f（x）的极值点，求m，并讨论f（x）的单调性；（2）当m≤2时，证明：f（x）＞0.

解：（1）略.

（2）当m≤2，x∈（-m，+∞）时，ln（x+m）≤ln（x+2），故只需证明当m=2时，f（x）＞0，即证明ex-ln（x+2）＞0.

下面证明ex≥x+1≥ln（x+2）（x＞-2，等号不同时成立）.

设g（x）=ex-（x+1），则g′（x）=ex-1.令g′（x）=0，解得x=0.

当x∈（-∞，0）时，g′（x）＜0，g（x）单调递减；当x∈（0，+∞）时，g′（x）＞0，g（x）单调递增.

所以g（x）≥g（0）=0，即ex≥x+1（当x=0时取等号）.

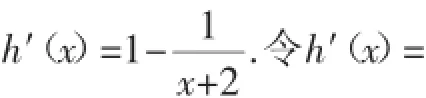
设h（x）=（x+1）-ln（x+2），则0，解得x=-1.当x∈（-2，-1）时，h′（x）＜0，h（x）单调递减；当x∈（-1，+∞）时，h′（x）＞0，h（x）单调递增.所以h（x）≥h（-1）=0，即x+1≥ln（x+2）（当x=-1时取等号）.

综上所述，当m≤2时，f（x）＞0.

纵观近年来的全国各地高考题，大多把导数中的不等式问题作为压轴题，命题者往往在求导函数或者在求导函数的零点上设置障碍，使得原函数的性态不易得到.而对学生来讲，求解这类题目的关键则是对函数进行适当地转化变形，将这些复杂的函数转化成相对简单的函数，从而找到解题的方法.