Boundedness in Asymmetric Quasi-periodic Oscillations

XING XIU-MEIMA JINGAND JIAO LEI

(1.School of Mathematics and Statistics,Yili Normal University,Yili,Xinjiang,835000)

(2.School of Science,Nanjing University of Science and Technology,Nanjing,210094)

Boundedness in Asymmetric Quasi-periodic Oscillations

XING XIU-MEI1,MA JING1AND JIAO LEI2,*

(1.School of Mathematics and Statistics,Yili Normal University,Yili,Xinjiang,835000)

(2.School of Science,Nanjing University of Science and Technology,Nanjing,210094)

Communicated by Li Yong

In the paper,by applying the method of main integration,we show the boundedness of the quasi-periodic second order dif f erential equationx′′+ax+−bx−+ϕ(x)=p(t),wherea/=bare two positive constants andϕ(s),p(t)are real analytic functions.Moreover,thep(t)is quasi-periodic coeffi cient,whose frequency vectors are Diophantine.The results we obtained also imply that,under some conditions, the quasi-periodic oscillator has the Lagrange stability.

boundedness,quasi-periodic,KAM theorem

1 Introduction

In 1999,Fabry and Mawhin[1]suggested studying the boundedness of all the solutions for the following dif f erential equation:

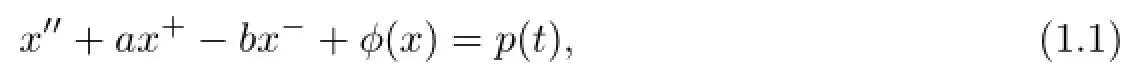
whereare two positive constants,p(t)is a periodic function,x+=max{x,0}andx−=max{−x,0}.Dancer[2]studied the periodic and Dirichlet boundary value problems for(1.1).Many authors are also concerned with the Lagrange stability of this equation.The fi rst boundedness result for(1.1)is due to Ortega.In[3],Ortega obtained the stability for

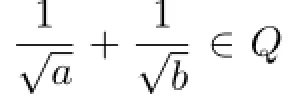
are f i nite.

Firstly,we introduce some basic notations,properties and lemmas which are used in this paper.

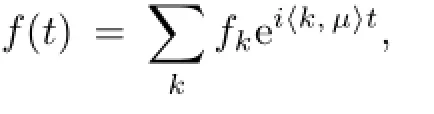
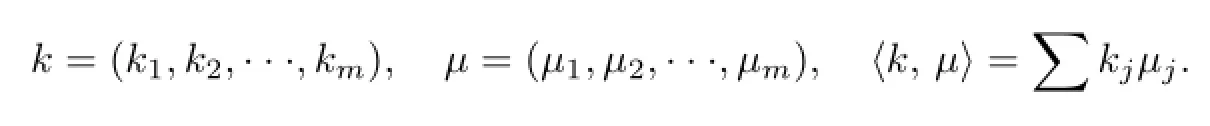
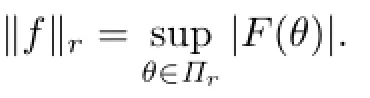
Lemma 1.1[7]The following statements are true:

(i)Let f(t),g(t)∈Q(µ).Then g(t+f(t))∈Q(µ).

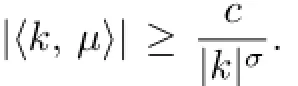
Then the inverse relation is given by t=α−1τ+h1(τ)and h1(τ)∈Q(µ/α).

Sun[11]considered the map

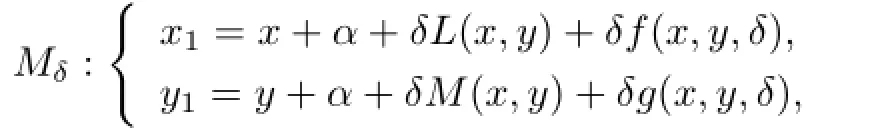
whereL,M,fandgare quasi-periodic inxwith the frequencyµand real analytic in the complex neighborhood of R×[a,b].Assume thatf(x,y,0)=g(x,y,0)=0 and theµsatisf i es the Diophantine condition:

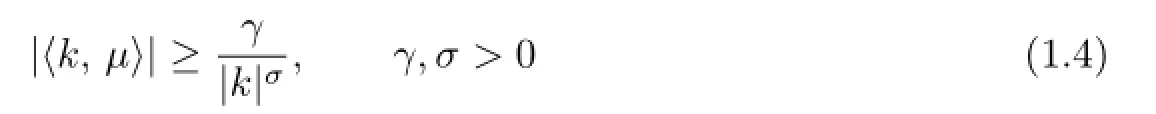
for all integerk=(k1,k2,···,km)0.Furthermore,suppose that the mapMδhas the intersection property,that is,for every Jordan curvey=φ(x)which is homotopic to the line satisf i esMδ(Γ)Sun obtained the following two theorems.

Theorem 1.1([11],Theorem 2.3)Ifµ1,µ2,···,µmand2π/α are rational independent and

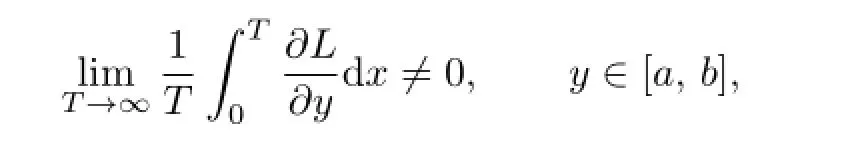
then there exists Δ＞0such that if0＜δ＜Δ,the map Mδhas an invariant curve y=ϕ(x), where ϕ(x)is real analytic and quasi-periodic with the frequencyµ.

Theorem 1.2([11],Theorem 2.4)are rational dependent.Lsatisf i es

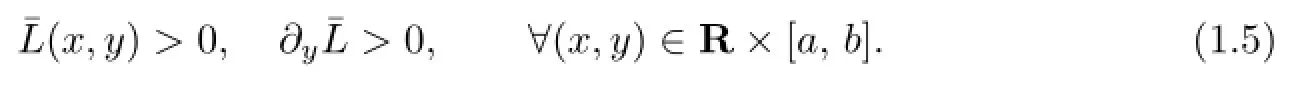
In addition,there is a real analytic function I(x,y)≡I(x+α,y)satisfying

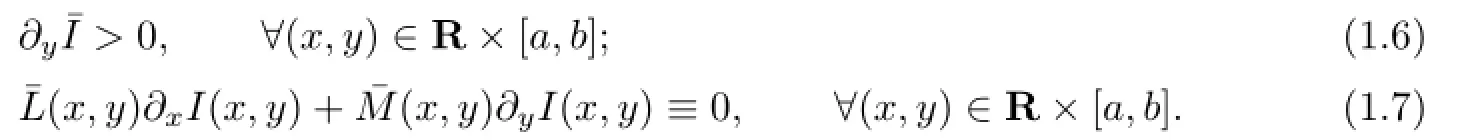
Moreover,suppose that there are two numbersandwith

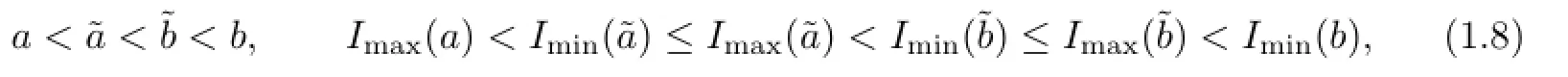
where

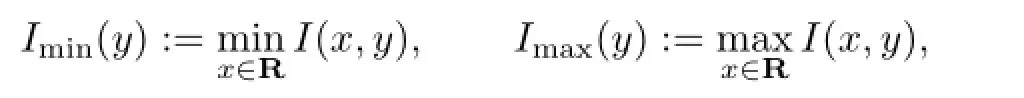
then there exists a Δ＞0such that if0＜δ＜Δ,the map Mδhas an invariant curve which is of the form y=ϕ(x),where ϕ(x)is real analytic and quasi-periodic with the frequencyµ, and the constant Δ＞0depends on a,b,˜a,˜b,L,M and I.

2 Boundedness of Quasi-periodic Oscillations

In this section,we f i rst introduce some notations,second state our main theorem on boundedness of asymmetric quasi-periodic oscillations,last give some of the lemmas and transformations which are used in the proof of Theorem 2.1.

Denote byC(t)the solution of

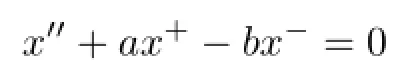
with the initial condition

The derivative ofC(t)is denoted by−S(t).It is easy to verify thatC(t)andS(t)are of 2πωfortandC(t)is second order dif f erential,where

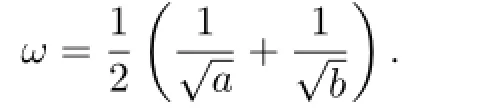
C(t)is even and can be given by

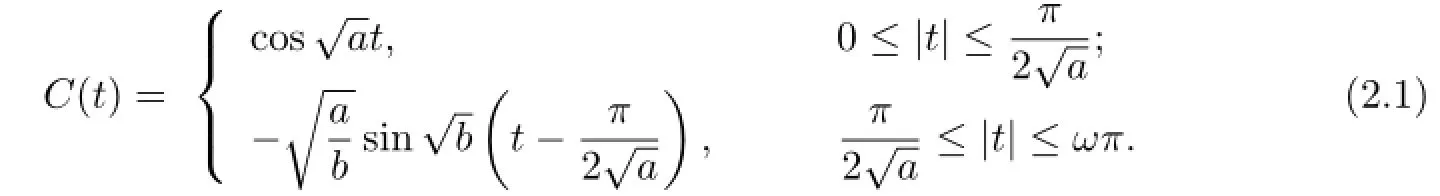
Moreover,

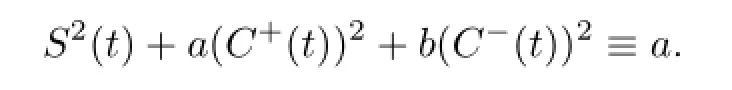
For a given quasi-periodic functionp(t),let

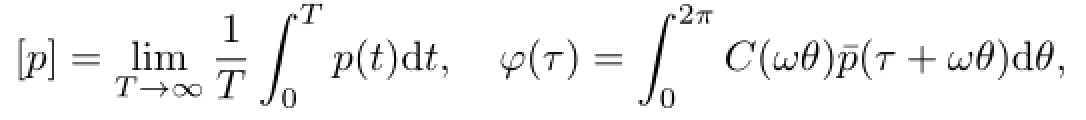
where

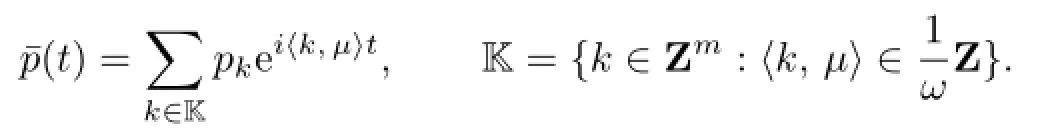
Now we can state our main theorem.

Theorem 2.1Suppose that(1.3)and(1.4)hold.Then

(i)are rational independent and

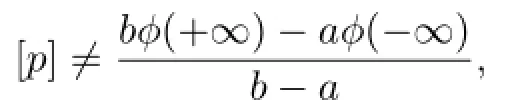
then all the solutions of(1.1)are def i ned for all t∈Rand

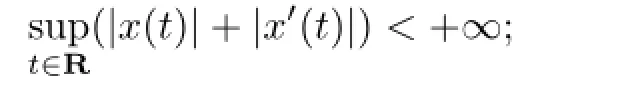
(ii)Ifµ1,µ2,···,µmandare rational dependent and

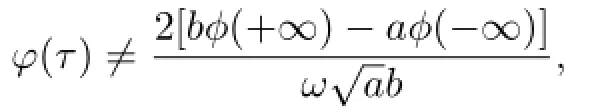
then all the solutions of(1.1)are def i ned for all t∈Rand

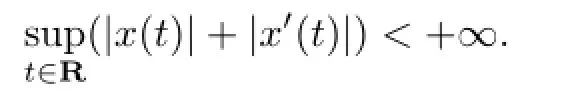
Letx′=−y.Then(1.1)is equivalent to the following system:

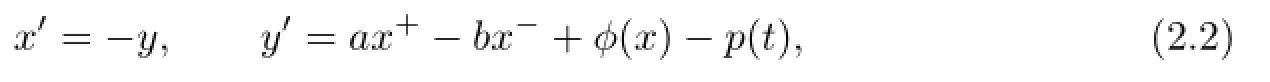
and the Hamiltonian function is

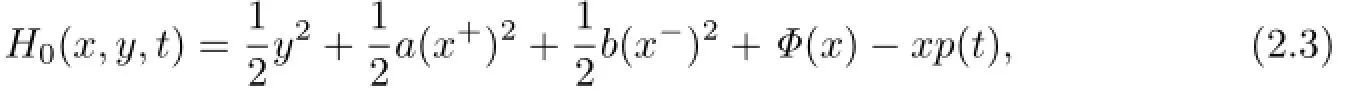
where

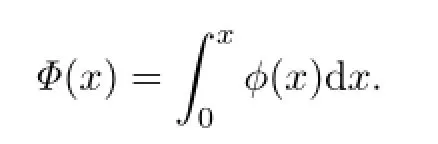
Throughout this paper,we denoteC＞1 universal positive constants not concerning their quantities.

Next we state Lemmas 2.1–2.2 and Lemma 3.2 in the paper.The proof of Lemmas 2.1–2.3 is similar to the proof of Lemmas 3.1–3.2 and Lemma 4.3 in[12].The conclusion of Lemma 3.2 in this paper can be obtained from the properties 3.1 and 3.2 in[11].

Lemma 2.1The unique solution(x(t;t0,x0,y0),x(t;t0,x0,y0))of(2.2)satisfying

exists on the whole t-axis for all(x0,y0)∈R2and all t0∈R.

Under the transformationΨ:R+×S1→R2 withr＞0 andθ(mod 2π),given by the formulae:

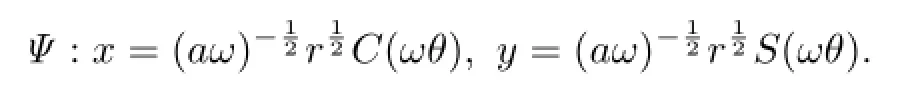
The Hamiltonian functionH0(x,y,t)is transformed into

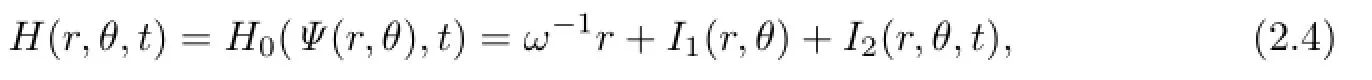
where

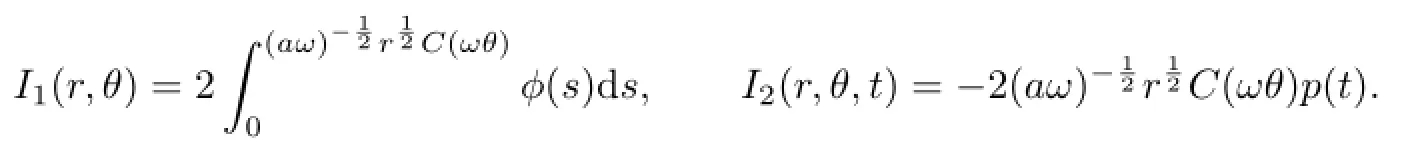
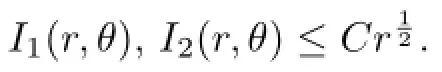
Let

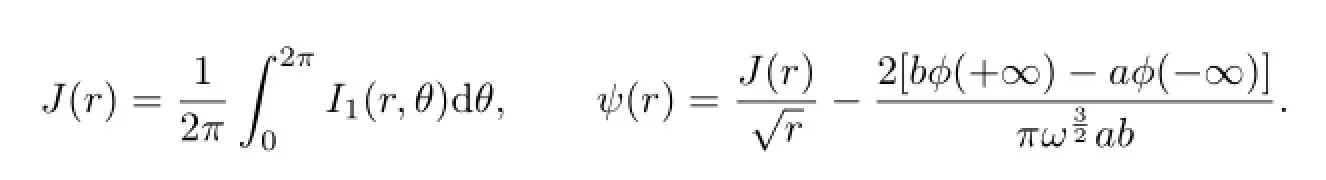
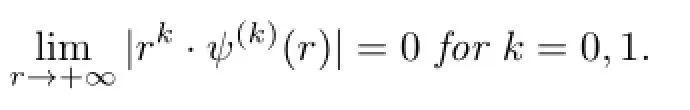
Note thatrdθ−Hdt=−(Hdt−rdθ).This means that if we can solver=r(H,t,θ) from(2.4),thenr(H,t,θ)is the Hamiltonian function of the following system:

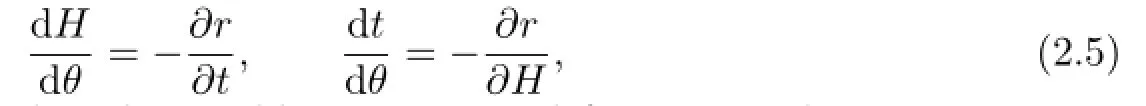
where the new action,time and angle variables areH,tandθ,respectively.

From(2.4)and Lemma 2.2,it follows that

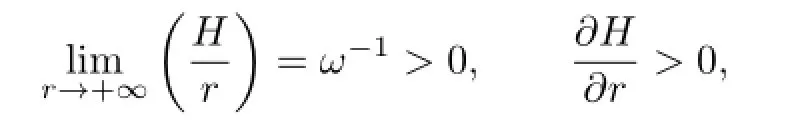
ifr≫1.By the implicit function theorem,we know that there is a functionR(H,t,θ)such that

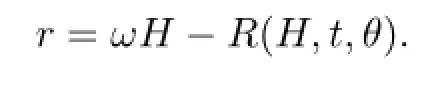
Moreover,forH≫1,

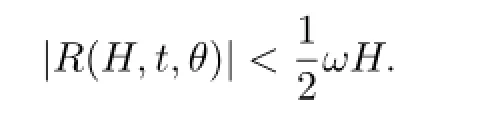
Hence we can write the functionrinto the form

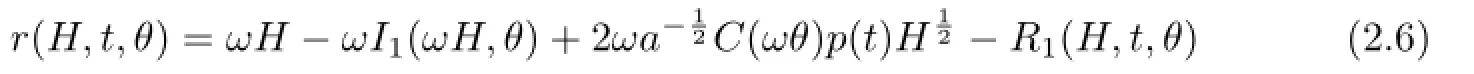
and|R1(H,t,θ)|＜C.

Let

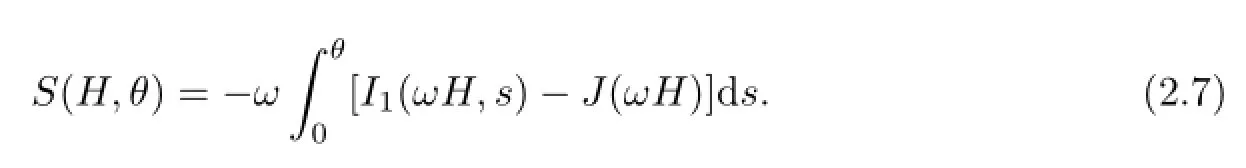
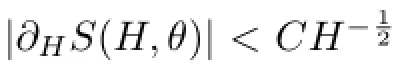
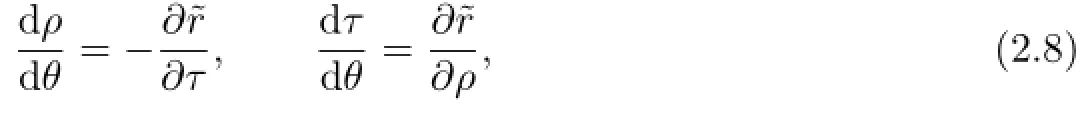
where

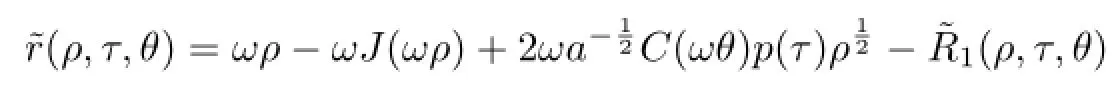
and

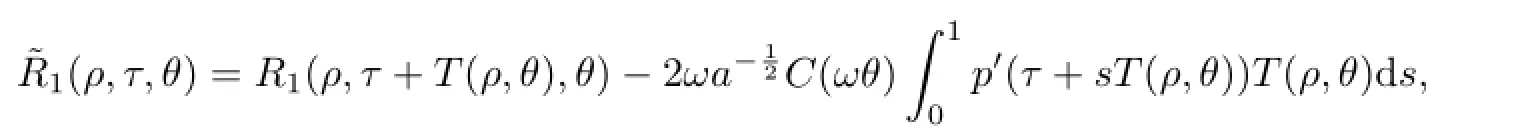
whereT(ρ,θ)=∂ρS(ρ,θ).With the help of Lemmas 2.2 and 2.3 together with(2.7),we have,forρ≫1,θ∈S1,

Due to Lemma 1.1 and the def i nitionΨ1,(2.8)is quasi-periodic inτ,frequency still isµ.

3 The Proof of Theorem 2.1

This section is divided into two parts.First we give an expression of the Poincar´e map of the system(2.8),and then prove Theorem 2.1.

We introduce a new variablevvarying in the closed interval[γ−1,γ]and a small positive parameterδby the formula

where the positive constantγ∈(1,+∞)is determined below by(3.10).Obviously,

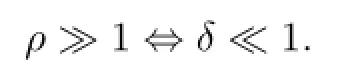
In the new action and angle variables(v,τ),the system(2.8)can be written in the form

where

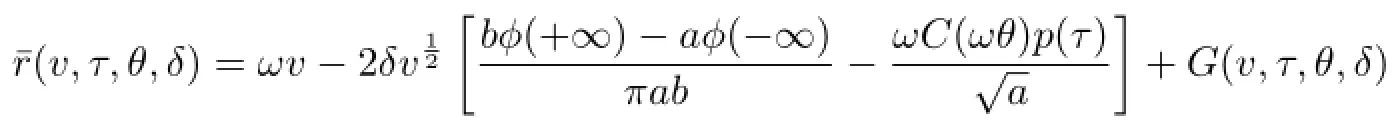
and

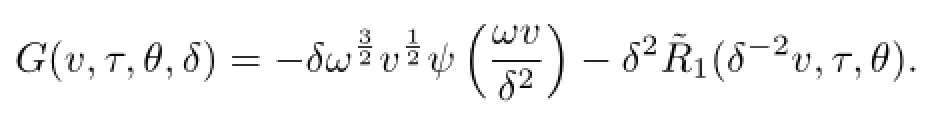
By Lemma 2.3 and formula(2.9),fork+l≤1,it is easy to show that

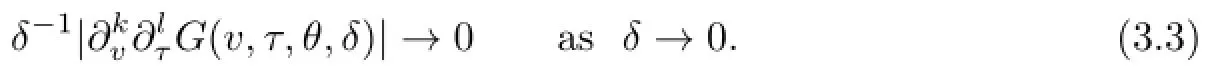
Now we write the system(3.2)explicitly

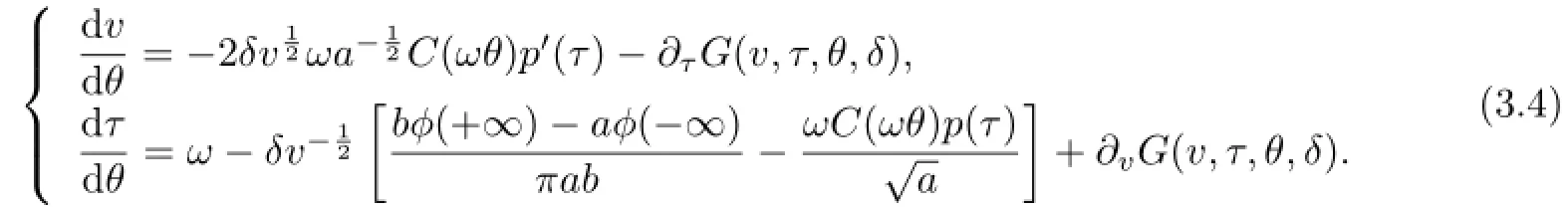
From(3.3),it follows that,ifδ≪1,then the solution(v(θ,v0,τ0),τ(θ,v0,τ0))with the initial condition(v(0,v0,τ0),τ(0,v0,τ0))=(v0,τ0)exists inθ∈[0,4π]for any(v0,τ0)∈[γ−1,γ]×[0,2π].The solution(v(θ,v0,τ0),τ(θ,v0,τ0))has the following expression:

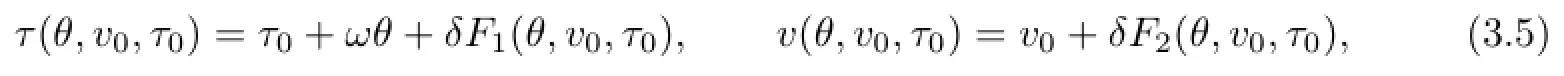
whereF1,F2≤Csatisfying

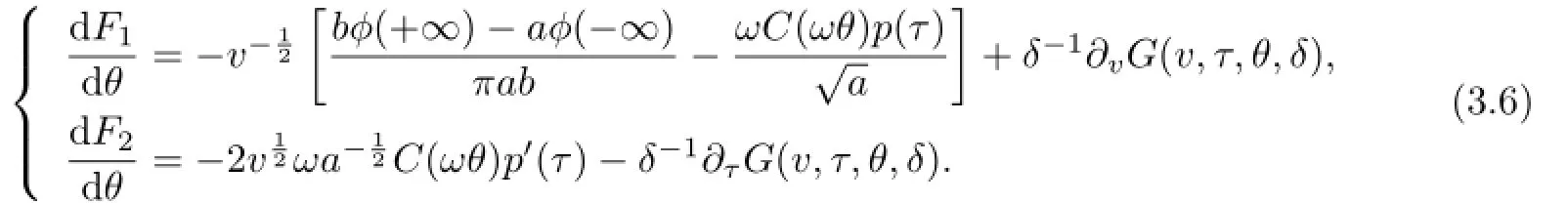
Integrating(3.6)from 0 to 2π,as in the proof in[12],we have

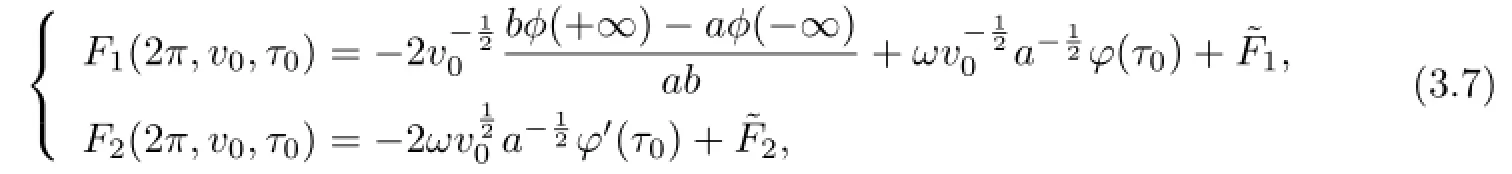
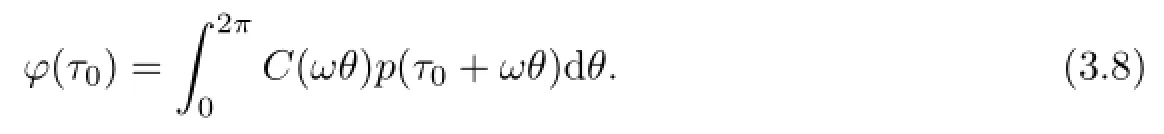
(3.5)together with(3.7)implies the time 2πmapping of(3.4)is of the form.

Lemma 3.1

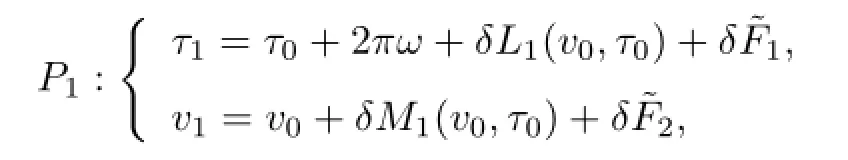
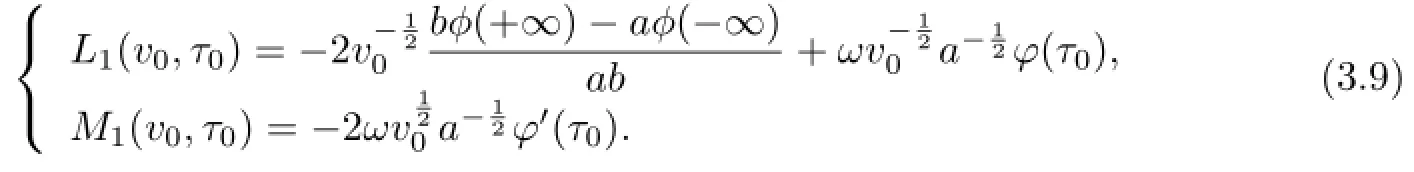
Lemma 3.2[11]The mapping P1has the intersection property in the domain[γ−1,γ]×S1for every δ≪1.

Proof of Theorem 2.1Ifµ1,µ2,···,µmandare rational independent.From(3.8) and(3.9),we have

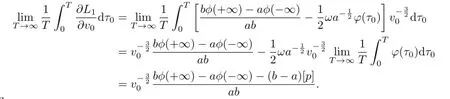
When

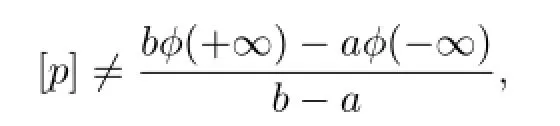
i.e.,

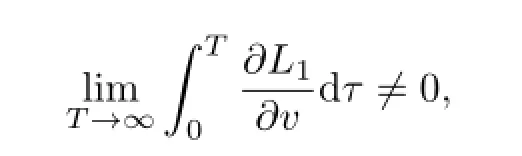
we know that the mappingP1has invariant curves in the domain R×[γ−1,γ]in[11]ifδis suffi ciently small.So the boundedness of solutions of(1.1)are guaranteed by Theorem 1.1.

Ifandare rational dependent.De fi ne a map:(v,τ)→(u,τ)by the formulaeu=v−1,τ=τ.Under theΨ2,theP1is transformed into a new map

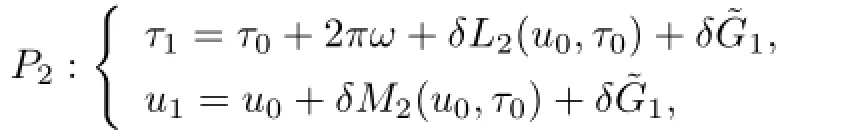
where

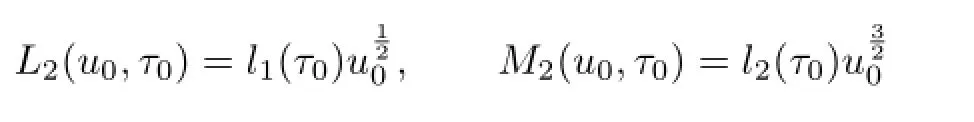
with

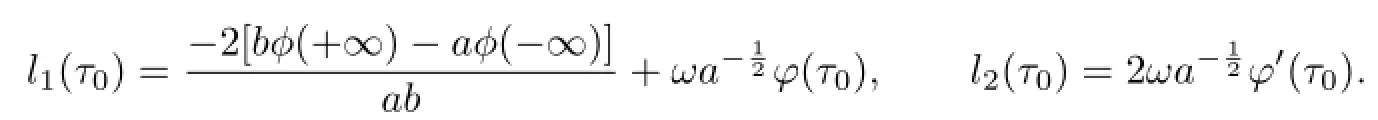
DenoteAγ=[γ−1,γ]×R.Due to

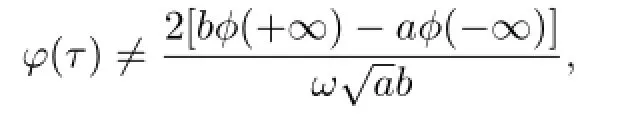
without loss of generality,we assume that

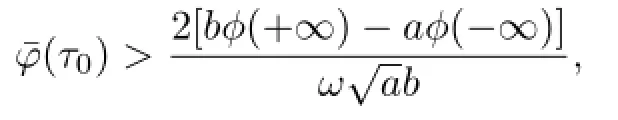
then

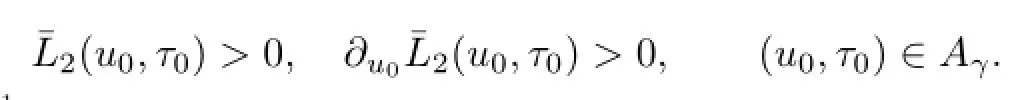
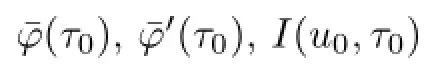
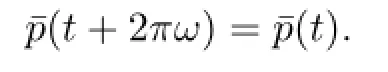
It is easy to verify that

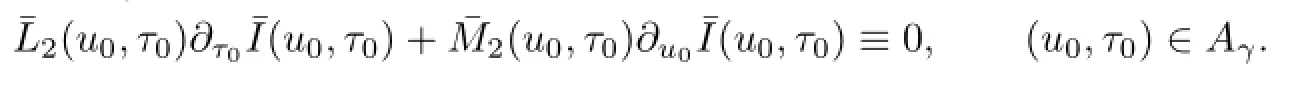
Denote

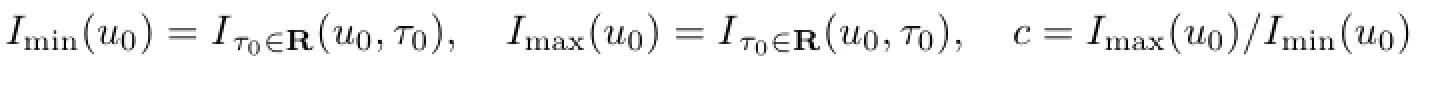
and

Choose

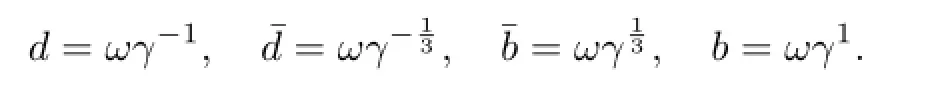
It is obviously thatand

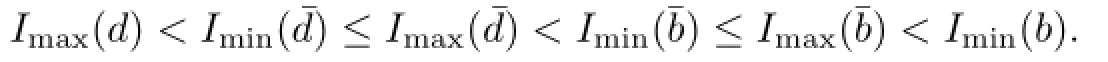
Now we have verif i ed that all the conditions(1.5)–(1.8)of Theorem 1.2 for the mappingP2.Hence the mappingP2has invariant curves in the domain R×[γ−1,γ]ifδis suffi ciently small as well as the boundedness of the solution of(1.1).Thus we complete the proof of Theorem 2.1.

[1]Fabry C,Mawhin J.Oscillations of a forced asymmetric oscillator at resonance.Nonlinearity, 2001,21:493–505.

[2]Dancer E N.On the Dirichlet problem for weakly nonlinear partical equation.Proc.Roy.Soc. Edinburgh Sect.A,1977,76:283–300.

[3]Ortega R.Asymmetric oscillators and twist mappings.J.London Math.Soc.,1996,53(2): 325–342.

[4]Liu B.Boundedness in asymmetric oscillations.J.Math.Anal.Appl.,1999,231(2):355–373.

[5]Wang X.Invariant tori and boundedness in asymmetric oscillations.Acta Math.Sin.(Engl. Ser.),2003,19:765–782.

[6]Yuan X.Quasiperiodic motions for asymmetric oscillations.Acta Math.Sin.(Engl.Ser.),2001, 17(2):253–262.

[7]Liu B.Invariant curves of quasi-periodic reversible mappings.Nonlinearity,2005,18:685–701.

[8]Liu B.The stability of the equilibrium of quasi-periodic planar Hamiltonian and reversible systems.Sci.China.,2010,53:125–136.

[9]Wu C,Wang Y.The stability of the elliptic equilibrium of quasi-periodic Hiltonian systems.Acta Math Sin.(Engl.Ser.),2010,26(7):1–6.

[10]Qian D,Sun X.Invatiant tori for asymptoticaly linear impact oscillators,Sci.China,2006, 49(4):669–687.

[11]Sun X.The Lagrangr stability of quasi-periodic impacr oscillators.PhD thesis.Suzhou:Su Zhou University,2009.

[12]Liu B.Boundedness in nonlinear oscillations at resonance.J.Dif f erential Equations,1999, 153(1),142–174.

tion:34C15,70H08

A

1674-5647(2017)02-0121-08

10.13447/j.1674-5647.2017.02.03

Received date:Aug.12,2015.

Foundation item:The NSF(201442137-26)of Xinjiang.

*Corresponding author.

E-mail address:xingxm09@163.com(Xing X M),jiaolei0104@163.com(Jiao L).