液态聚乙二醇CH2剪切振动和扭转振动<br/>——拉曼光谱和密度泛函理论计算

1 引言

以氧乙烯基(EO)为重复单元的聚氧乙烯(PEO)因自身的亲水性而常用作两亲分子的亲水端。如，烷基聚氧乙烯醚非离子性表面活性剂和聚氧乙烯聚氧丙烯醚嵌段共聚物中的氧乙烯基。聚氧乙烯基(分子)主链中－CH2－O－、－CH2－CH2－等结构单元的旋转使单条PEO分子的构象稳定性会随外部因素(相态、温度、溶剂、离子)等的变化而变化。因此，PEO的理化和应用性能与聚合度m和EO空间取向等密切相关。

晶态PEO的红外光谱、拉曼光谱和X射线衍射谱的研究结果显示，PEO分子链为螺旋(helix)结构，7个EO单元形成2个完整螺旋(简称7/2螺旋)1－4。其中，绕O－CH2，CH2－CH2，和CH2－O单键的内旋转构象分别为反式构象(T)，偏转构象(G)和T(简称TGT构象)5。以TGT为重复单元的螺旋链具有两个二重对称轴，一个轴穿过氧原子，另一轴平分C－C键。X射线衍射光谱显示，PEO晶体的单位晶包属于单斜晶系，空间群为P21/a，内含四条螺旋分子链6。在过去50多年里，(TGT)m构象在解释晶态PEO结构与物性关系中发挥着关键作用。例如，基于(TGT)m的简正振动计算频率能与常温晶态PEO实验振动频率吻合1,2,7,8。(TGT)m构象异构体的链变形振动和C－O内旋转运动得到低温远红外和拉曼光谱的印证9。

与晶态PEO不同，液态纯PEO分子链的晶格堆积效应消失，主链单键旋转产生大量构象异构体共存。但迄今为止，液态PEO的光谱研究一直沿用(TGT)m构象3,10。例如，水溶液中PEO与水的氢键作用3，液态或水溶液中PEO的结构有序性10，水溶液中PEO与Mn+相互作用4,11－17，温度和H2O量对－C－C－(G构象)和－C－O－(T构象)结构的影响等都只考虑(TGT)m构象18，而其它构象的作用一概被忽略。究其原因，主要是频率相近的振动峰的叠加使液态PEO的振动光谱较晶态时大为展宽，谱带指认变得相当困难，阐明其它构象作用的相关研究相当稀少。为此，本文采用密度泛函理论计算方法，结合拉曼光谱实验手段，研究常温下液态PEO400构象异构体的结构和振动光谱。

图1 －[CH2CH2O]－单元的六种构象Fig.1 Six conformations of the－[CH2CH2O]－unit

2 实验和理论计算

2.1 试剂与仪器

2.1.1 实验药品

平均分子量400聚乙二醇(PEO400)，化学结构式HO－(CH2CH2O)m－H(m=10)，(纯度99.0%，Sigma-Aldrich公司)；平均分子量1500聚乙二醇(PEO1500)，化学结构式HO－(CH2CH2O)m－H (m=34)，(纯度99.0%，Sigma-Aldrich公司)。

2.1.2 实验仪器

傅里叶变换红外光谱仪(Nicolet57000.09/cm，美国尼高力仪器公司)，显微拉曼光谱仪(*/PI Action TriVista，美国Princeton Instruments Inc)。

2.2 实验方法

2.2.1 傅里叶变换红外(FT-IR)光谱实验

实验使用Nicolet57000.09/cm傅里叶红外光谱仪。用毛细管蘸取少量液态的样品滴在KBr窗片上，并用另一片KBr窗片盖在上面，使液膜均匀分布待测；实验扫描空气作为背景，扫描次数32次，扫描波数范围4000－400 cm－1。

2.2.2 显微拉曼光谱

实验使用*/PI Action Tri Vista显微拉曼光谱仪(micro-Raman)。实验样品直接放进比色皿(10 mm× 10 mm，2.5 mL)中，在488 nm激光波长下测定，为尽可能提高信噪比，每张光谱大约采集20－200 s。

2.3 理论计算

分子几何结构优化和振动频率计算在B3LYP/ 6-31G(d)理论水平下获得，所有量子化学计算均由Gaussian 09W程序包完成。

3 结果和讨论

3.1 构象结构

PEO分子主链的单键旋转产生构象异构体。按现行标记方法18和分子式HO(CH2CH2O)10H顺序，图1给出6种EO构象标记，其中，数字1、2和3分别标记O－C，C－C和C－O单键。TTT和TGT等名称中，反式构象T或扭转构象G表示以某个键(如标记2的C－C键)为中心的前后2个键(如标记1的O－C单键和标记3的C－O键)的相对空间位置。表1分别给出了C－O－C－C、O－C－C－O和C－C－O－C所形成的二面角数据，用以描述各构象的相对空间位置。以这6种EO构象为单元，构建了6种全同EO构象组合和3种随机EO构象组合的PEO400构象异构体，并采用密度泛函理论对9种初始结构进行结构优化。(TGG)10和(GGG)10构象异构体未能优化得到，主要原因是两个连续GG构象会导致OH基和CH2基上两个H原子在空间产生排斥力而不利于相关构象的稳定。

表1 B3LYP/6-31G(d)计算水平下获得的7种PEO400几何构象的能量和二面角Table 1 Seven geometric conformations of PEO400 and the corresponding dihedralangles computed using B3LYP/6-31G(d)levelof theory

图2 PCM溶剂模型和B3LYP/6-31G(d)计算水平下获得的7种代表性PEO400构象结构图Fig.2 Seven conformationalstructures of PEO400 obtained using the PCMsolventmodelat B3LYP/6-31G(d)levelof theory

穷尽不同构象异构体来阐明构象与特征振动频率大小的定量关系对构象数很有限的小分子体系是一种常规策略，已广泛用于光谱指认中。但这一策略对EO数较大的PEO体系不适合，因为其构象数随EO数的增加呈几何级数增加。因此，在有限的计算成本中必须避开穷尽PEO全部构象异构体的做法。

本文发现，决定CH2剪式振动和CH2扭转振动频率大小的关键因素是CH2CH2－O－CH2CH2链段的构象及其振动模式(详见本文2.3节)，当(TGT)10构象异构体被确定为主要成分时，只要CH2CH2－O－CH2CH2链段的构象及其振动模式穷尽了，就无需考虑更多其它EO构象组合的构象异构体的数量问题。图2示出(TTT)10、(TGT)10、(TTG)10、(GTG)10、(GTT-TTT-TTG-TTT)2-GTT-TTT、(GTG)6(GTT)2(GTG)2和(GTT)2(TTG)2(GTT)2(TTG)2(GTT)2等7种优化构象结构，它们已包含了全部4种CH2CH2－O－CH2CH2链段的构象和振动模式。表1列出它们的能量和部分二面角数据。由表1可见，真空和气相时，(TTT)10构象异构体的能量最低，稳定性依次为(TTT)10＞(TGT)10＞(TTG)10＞(GTG)10；而水溶剂模型时，(TGT)10构象能量最低，稳定性依次为(TGT)10＞(TTT)10＞(TTG)10＞(GTG)10。可见，引入水溶剂的极性效应，(TGT)10和(TTT)10的稳定性互换位次。由表1可见，3种非全同EO构象组合的PEO400构象异构体的能量介于(TGT)10和(GTG)10之间。

3.2 振动光谱

纯PEO400的液态傅立叶变换红外光谱和拉曼光谱，以及PEO400:H2O=1:1样品的拉曼光谱示于图3。图3可见，纯PEO400的液态拉曼谱带较晶态时要宽得多，预示有多种构象异构体共存。同时，水与PEO400的氢键相互作用对500－1600 cm－1频率区域的拉曼光谱强度模式影响不大，但会引起830和1238 cm－1等振动频率的些许位移。

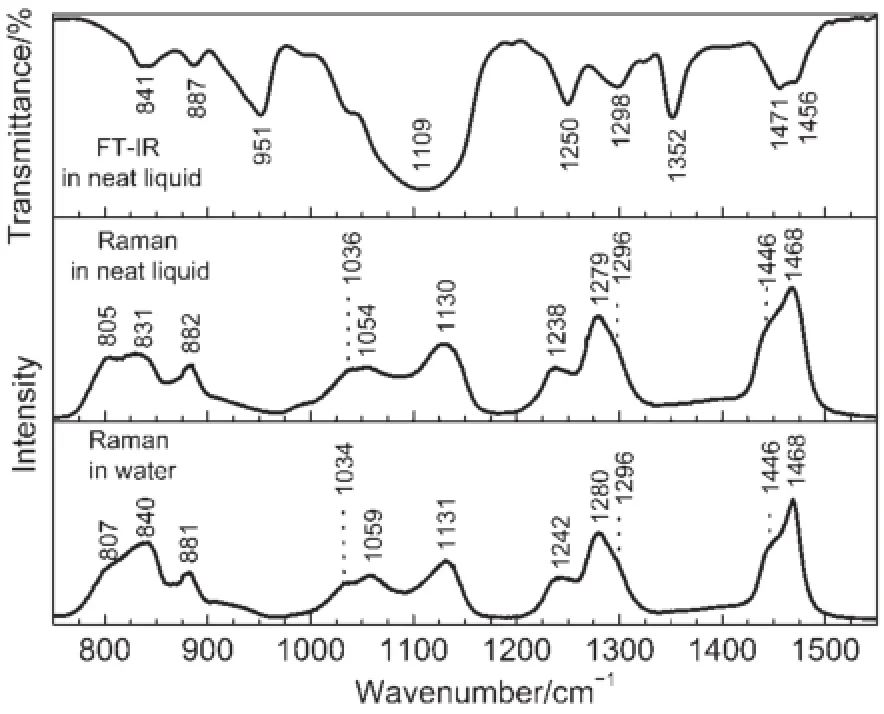
图3 纯PEO400液体的傅里叶变换红外光谱(上)和拉曼光谱(中)以及n(PEO400):n(H2O)=1:1样品的拉曼光谱(下) Fig.3 FT-IR(top)and Raman(middle)spectra of neat liquid PEO400,and Raman spectrum(bottom)of n(PEO400):n(H2O)=1:1 sample Raman excitation wavelength=488 nm

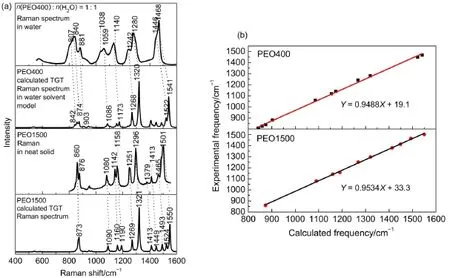
图4 (a)B3LYP/6-31G(d)理论水平下计算获得的TGT异构体拉曼光谱与样品实验拉曼光谱的比较和(b)主要实验频率与计算频率的线性回归拟合Fig.4(a)Comparison between the experimental Raman spectrum of sample and the calculated TGT Raman spectrum using B3LYP/6-31G(d)levelof theory and(b)linear regression fitting between main experimental Raman frequencies and the corresponding calculated ones Raman excitation wavelength=488 nm

为了验证密度泛函理论计算在预测聚氧乙烯醚聚合物的振动频率时的可靠性，开展了(TGT)34拉曼光谱的计算和PEO1500实验拉曼光谱的测量，结果示于图4(a)，其中虚线示出主要实验谱带与(TGT)34计算光谱带的试探性关联。图4(b)(下)示出实验和理论计算光谱主要振动峰间的线性回归拟合结果，结果显示，相关系数R=0.999，标准偏差=6.99，两者吻合良好，说明密度泛函理论计算方法是可靠的。

表2 PCM溶剂模型和B3LYP/6-31G(d)计算水平下(TGT)10构象异构体的计算振动频率、PEO400实验振动频率和光谱指认Table 2 Calculated vibrationalfrequencies of(TGT)10conformation using PCMsolvent modeland B3LYP/6-31G(d)levelof theory,the experimentalfrequencies and the assignments of PEO400

采用PCM溶剂模型下的B3LYP/6-31G(d)计算水平对图2中7种构象异构体的优化结构进行了振动频率计算。表2列出了(TGT)10构象异构体的计算频率与PEO400液态实验频率的比较，以及初步的光谱指认。图4(a)(上)展示(TGT)10的计算拉曼光谱与PEO400实验拉曼光谱的比较，图4(b)(上)展示了相关振动频率的线性回归拟合结果，相关系数R=0.998，标准偏差=11.5。图4和表1、表2结果显示，能量最低的(TGT)10构象异构体的拉曼光谱强度模式能与实验拉曼光谱大致吻合，表明溶液中(TGT)10构象结构是PEO400的主要存在形式之一，沿用(TGT)10构象指认液态拉曼光谱主要谱峰是合理的，但离全面阐述液态光谱仍有距离。例如，(TGT)10构象结构的计算拉曼光谱与实际光谱的强度模式如1446、1296、1131、1059、1034、881、840和807 cm－1等的峰强度上，存在较大差异。部分原因可能是所采用的密度泛函理论计算水平还不够高级，使得(TGT)10的计算拉曼峰强度与实际光谱有偏差，但更主要的原因应该是其它共存构象的叠加贡献。

3.3 CH2CH2－O－CH2CH2特征链段的振动模式及其对实验光谱的贡献

为了洞察不同CH2CH2－O－CH2CH2链段构象的不同CH2振动模式对实验光谱的贡献，图5示出由PCM溶剂模型和B3LYP/6-31G(d)计算水平获得的7种PEO400构象异构体的计算拉曼光谱。仔细研究1150－1600 cm－1光谱区域内各主要拉曼谱峰的振动模式后发现，它们可分别归类为CH2CH2OCH2CH2链段4种构象的CH2剪切振动和CH2扭转振动，具体见图6。相关的CH2剪切振动和CH2扭转振动模式归纳如下。

(TGT)10构象异构体的CH2CH2－O－CH2CH2链段为GTTG构象(简称GTTG链段，下同)。因此，1541、1522、1320和1268 cm－1等4个拉曼峰都与GTTG构象有关。其中，1541 cm－1峰为CαH2/Cα′H2同向+CβH2/Cβ′H2同向及CαH2/CβH2背向+Cα′H2/Cβ′H2背向剪切振动(简称α/α′+β/β′两两同向CH2剪切振动，下同)；1522 cm－1峰为α/β+α′/β′两两同向CH2剪切振动；1320 cm－1峰为α/α′+β/β′两两同向CH2扭转(twist)振动；1268 cm－1峰为α/β+α′/β′两两同向CH2扭转振动。

(TTT)10构象异构体为TTTT链段。1554和1310 cm－1峰被分别指认为全同CH2剪切振动和全同CH2扭转振动。

(TTG)10构象异构体为TGTT链段。1548 cm－1为α/β′+α′/β两两同向剪切振动；1519 cm－1为α/β+α′/β′两两同向CH2剪切振动；1330 cm－1为α/β+α′/β′两两同向CH2扭转振动。

(GTG)10构象异构体为TGGT链段。1536 cm－1为α/β/α′同向CH2剪切振动；1519 cm－1为β/α′/β′同向CH2剪切振动；1355 cm－1为α/β+α′/β′两两同向CH2扭转振动。

(GTT-TTT-TTG-TTT)2-GTT-TTT构象异构体为TTTT、TGTT和TGGT链段。1555 cm－1峰为TTTT链段的全同CH2剪切振动；1523 cm－1峰为TGTT链段中G左边α/β同向CH2剪切振动；1544 cm－1峰为TTTT(主要)和TGTT两种链段的CH2剪切振动；1330 cm－1峰为TGTT链段中G左边α/β同向CH2扭转振动；1312 cm－1峰为TTTT链段的全同CH2扭转振动。

图5 7种PEO400构象异构体的1300－1600 cm－1区域的计算拉曼光谱Fig.5 Calculated Raman spectra of seven PEO400 conformations in 1300－1600 cm－1region

(GTT)2(TTG)2(GTT)2(TTG)2(GTT)2构象异构体为TGGT、TGTT和TTTT链段。1558 cm－1峰为TTTT链段的全同CH2剪切振动，与(GTT-TTTTTG-TTT)2-GTT-TTT构象异构体的1555 cm－1峰的振动模式相同；1536 cm－1峰为TGGT链段的全同CH2剪切振动；1524 cm－1峰为TGTT链段G型CO键左边α/β同向CH2剪切振动，与(GTT-TTTTTG-TTT)2-GTT-TTT构象异构体的1523 cm－1峰的振动模式相同；1344 cm－1峰为分子主链末端TGGT链段的α/β+α′/β′两两同向CH2扭转振动。1328 cm－1峰为TTTT链段的全同CH2扭转振动。

(GTG)6(GTT)2(GTG)2构象异构体为TGGT、TGTT和TTTT链段。1536 cm－1峰为TGGT链段的全同CH2剪切振动，与(GTT)2(TTG)2(GTT)2(TTG)2(GTT)2构象异构体的1536 cm－1峰的振动模式相同。1521 cm－1峰为TGTT链段的CH2剪切振动；1349 cm－1为TGGT链段的α/β+α′/β′两两同向CH2扭转振动，与(GTT)2(TTG)2(GTT)2(TTG)2(GTT)2构象异构体的1344 cm－1峰的振动模式相同；1328 cm－1峰为TGTT链段的CH2扭转振动；1356 cm－1峰为分子主链中部TGGT链段的α/β+α′/β′两两同向CH2扭转振动。

基于上述振动指认，我们注意到振动频率大小与CH2CH2－O－CH2CH2链段构象的振动模式密切相关。其频率大小顺序可归纳为。

剪切振动频率：TTTT链段全同CH2剪切振动频率(1554－1558 cm－1)＞GTTG链段的α/α′+β/β′两两同向CH2剪切振动频率(1541－1548 cm－1)＞TGGT链段的全同CH2剪切振动频率(1536 cm－1)＞GTTG链段的α/β+α′/β′两两同向CH2剪切振动频率，或者TGTT链段G型C－O键左边CαH2/CβH2同向剪切振动频率(1519－1524 cm－1)。

扭转振动频率：链中部TGGT链段的α/β+α′/ β′两两同向CH2扭转振动(1355－1356 cm－1)＞分子主链末端TGGT链段的α/β+α′/β′两两同向CH2扭转振动(1344 cm－1)，或者TGGT链段的α/β+α′/β′两两同向CH2扭转振动(1349 cm－1)＞TGTT链段G左边α/β同向CH2同向扭转振动，或α/β+α′/β′两两同向CH2扭转振动(1330 cm－1)，或TGTT链段的CH2扭转振动(1328 cm－1)＞GTTG链段的α/α′+β/β′两两同向CH2扭转振动(1320 cm－1)＞TTTT链段的全同CH2扭转振动(1310－1312 cm－1)＞GTTG链段的α/β+α′/β′两两同向CH2扭转振动(1268 cm－1)。

基于上述特征链段的振动频率分析，参照基于(TGT)10异构体的实际拉曼光谱的初步指认，对图4中1296和1446 cm－1等谱峰进行了归属，并对各构象异构体的特征链段的贡献进行了探讨。

首先，实验拉曼光谱中1468 cm－1拉曼峰被指认为(TGT)10异构体GTTG链段的α/α′+β/β′两两同向CH2剪切振动。因为TTTT链段全同CH2剪切振动频率(1554－1558 cm－1)＞GTTG链段的α/α′+β/β′两两同向CH2剪切振动频率(1541－1548 cm－1)，故1468 cm－1峰右侧(高频侧)的部分强度被归属为(TTT)10等构象异构体的TTTT链段的全同CH2剪切振动。我们注意到，纯液态时1468 cm－1拉曼峰右侧半峰宽较水溶液时大～4 cm－1，这说明(TTT)10构象异构体和各异构体TTTT链段在纯液态时有明显的布居。水的存在不利于TTTT链段的布局。同理，1446 cm－1峰被归属为各异构体TGTT链段的CH2剪切振动。

其次，因实验拉曼光谱中1280 cm－1峰被指认为(TGT)10异构体GTTG链段的α/α′+β/β′两两同向CH2扭转振动(1320 cm－1)，故实验拉曼光谱中1296 cm－1被指认为(TTG)10异构体TGTT链段的α/β+α′/ β′两两同向CH2扭转振动(计算频率1330 cm－1)(主要)。(GTT-TTT-TTG-TTT)2-GTT-TTT异构体TGTT链段的α/β同向CH2扭转振动(计算频率1330 cm－1)和(GTG)6(GTT)2(GTG)2构象异构体TGTT链段的的CH2扭转振动(计算频率1328 cm－1)对1296 cm－1峰也有一定的贡献。概括起来，1296 cm－1峰可归属为各异构体TGTT链段的CH2扭转振动。

图6 与描述CH2剪切振动和CH2扭转振动相关的4种CH2CH2－O－CH2CH2构象Fig.6 Four CH2CH2－O－CH2CH2conformations associated with the description of CH2scissor and CH2twist vibrations

4 结论

本文采用密度泛函理论计算方法结合红外和拉曼光谱实验手段研究了常温液态下PEO400构象异构体的结构和振动光谱。基于6种EO重复单元构象的定义，构建并优化得到了4种全同EO构象组合(TGT)10、(TTT)10、(TTG)10和(GTG)10，以及3种其它EO构象组合的PEO400构象异构体，并在PCM溶剂模型和B3LYP/6-31G(d)理论水平下获得了它们的振动光谱，重点开展了CH2剪切振动和CH2扭转振动的模式分析，并将结果应用于液态和水溶液中的拉曼光谱指认。本文发现，决定CH2剪式振动和CH2扭转振动频率大小的关键因素是CH2CH2－O－CH2CH2链段的构象及其振动模式，当(TGT)10被确定为主要成分时，只要CH2CH2－O－CH2CH2链段的构象及其振动模式穷尽了，就可避开与其它EO构象组合相关的重要构象异构体数量穷尽的难题。具体结论如下：

(1)无论是4种全同EO构象组合(TGT)10、(TTT)10、(TTG)10和(GTG)10，还是其它任意EO构象组合的构象异构体，其CH2剪切振动和CH2扭转振动模式均与CH2CH2－O－CH2CH2链段的TTTT、TGTT、TGGT和GTTG构象相关。

(2)CH2剪切振动和扭转振动频率大小由链段的构象决定：

(i)TTTT链段全同CH2剪切振动＞GTTG链段α/α′+β/β′两两同向CH2剪切振动频率(1541－1548 cm－1)＞TGGT链段的全同CH2剪切振动频率(1536 cm－1)＞GTTG链段的α/β+α′/β′两两同向CH2剪切振动频率(1519－1524 cm－1)；

(ii)主链中部TGGT链段的α/β+α′/β′两两同向CH2扭转振动(1355－1356 cm－1)＞主链末端TGGT链段的α/β+α′/β′两两同向CH2扭转振动(1344－1349 cm－1)＞TGTTα/β+α′/β′两两同向CH2扭转振动(1330 cm－1)＞GTTG的α/α′+β/β′两两同向CH2扭转振动(1320 cm－1)＞TTTT链段的全同CH2扭转振动(1310－1312 cm－1)＞GTTG的α/β+α′/β′两两同向CH2扭转振动(1268 cm－1)。

(3)1296 cm－1峰可归属为各异构体TGTT链段的CH2扭转振动；1446 cm－1峰可归属为各异构体TGTT链段的CH2剪切振动；1468 cm－1峰右侧(高频侧)的部分强度被归属各异构体TTTT链段的全同CH2剪切振动。

(1)Miyazawa,T.;Fukushima,K.;Ideguchi,Y.J.Chem.Phys. 1962,37,2764.doi:10.1063/1.1733103

(2)Yoshihara,T.;Tadokoro,H.;Murahashi,S.J.Chem.Phys.1964, 41,2902.doi:10.1063/1.1726373

(3)Koenig,J.L.;Angood,A.C.J.Polym.Sci.A 1970,8,1787.

(4)Tadokoro,H.;Chatani,Y.;Yoshihara,T.;Tarahara,S.; Murahashi,S.Makromol.Chem.1964,73,109.

(5)Matsuura,H.;Miyazawa,T.J.Polym.Sci.A 1969,7,1735.

(6)Takahashi,Y.;Tadokoro,H.Macromolecules 1973,6,673.

(7)Matsuura,H.;Miyazawa,T.Bull.Chem.Soc.Jap.1968,41, 1798.

(8)Yakoyama,M.;Ochi,H.;Tadokoro,H.;Price,C. Macromolecules 1972,5,690.

(9)Rabolt,J.F.;Johnson,K.W.;Zitter,R.N.J.Chem.Phys.1974, 61,504.doi:10.1063/1.1681924

(10)Migliardo,F.;Magazù,S.;Caccamo,M.T.J.Mol.Struct.2013, 1048,261.doi:10.1016/j.molstruc.2013.05.060

(11)Chaurasia,S.K.;Singh,R.K.;Chandra,S.Vibrational Spectroscopy 2013,68,190.doi:10.1016/j.vibspec.2013.08.001

(12)Frech,R.;Huang,W.Macromolecules 1995,28,1246.

(13)Chatani,Y.;Fujii,Y.;Takayanagi,T.;Homma,A.Polymer 1990, 31,2238.

(14)Chatani,Y.;Okamura,S.Polymer 1987,28,1815.

(15)Iwamoto,R.;Saito,Y.;Ishihara,H.;Tadokoro,H.J.Polym.Sci. Polym.Phys.Ed.1968,6,1509.

(16)Yokoyama,M.;Ishihara,H.;Iwamoto,R.;Tadokoro,H.; Macromolecules 1969,2,184.

(17)Paoke,B.L.;Ratner,M.A.;Shriver,D.F.J.Phys.Chem.Solids 1981,42,493.

(18)Shephard,J.J.;Bremer,P.J.;McQuillan,A.J.J.Phys.Chem.B 2009,113,14229.doi:10.1021/jp905149z

CH2Scissor and Twist Vibrations of Liquid Polyethylene Glycol——Raman Spectra and Density Functional Theory Calculations

HAN Lei1PENGLi1CAILing-Yun1ZHENGXu-Ming1,*ZHANGFu-Shan2
(1Department of Chemistry,Zhejiang Sci-Tech University,Hangzhou 310018,P.R.China;2Technology Center,Hengan Group,Jinjiang 362261,Fujian Province,P.R.China)

Anew method is developed to effectively study the contributions ofvarious coexisting conformations to the actualvibrationalspectrum of liquid polyethylene oxide(PEO).By defining six conformations for the－(CH2CH2O)－unit,four isomers from the combinations of allthe same EOconformations[(TGT)10,(TTT)10, (TTG)10,and(GTG)10]and three isomers from the combinations ofother EO conformations were constructed. Their optimized geometric structures and the corresponding vibrationalfrequencies were then computed.The unified standards thatdescribe the differenttypes ofthe CH2scissor and CH2twistvibrationalmodes for PEO400 are proposed through the analysis of the normalmodes.The relationships between the four CH2CH2－OCH2CH2conformations and the various CH2scissor and CH2twist vibrational modes and frequencies are determined,and the results are used to assign the practicalvibrationalspectra.

Polyethylene oxide;Conformation;Raman spectrum;Density functionaltheory calculation

O641

10.3866/PKU.WHXB201702083

Received:November 28,2016;Revised:January 21,2017;Published online:February 8,2017.

*Corresponding author.Email:zxm@zstu.edu.cn;Tel:+86-571-86843699.

The projectwas supported by the National Natural Science Foundation of China(21473163)and National Basic Research Program of China(973) (2013CB834604).