自适应核时频分析方法的改进及应用

岳 龙， 刘怀山， 徐秀刚

(中国海洋大学 海底科学与探测技术教育部重点实验室，青岛 266100)

自适应核时频分析方法的改进及应用

岳 龙， 刘怀山， 徐秀刚

(中国海洋大学 海底科学与探测技术教育部重点实验室，青岛 266100)

提高地震信号的时频分辨率是时频分析研究的重点，传统的线性时频分析方法(短时傅里叶变换、小波变换、S变换)时频分辨率不高，而双线性时频分析方法(如魏格纳分布)时频分辨率高，但存在严重的交叉项干扰。自适应核时频分析方法，属于双线性时频分布，计算过程中采用随时间变化的最优核函数，在保证高分辨率的前提下，压制信号模糊域的交叉项干扰，提高了时频谱的可读性。对比了四种时频分析方法对于线性调频信号的分析效果，并将聚焦性更好的自适应核方法应用于实际资料，并利用改进的自适应核时频分析方法在瞬时属性提取和谱分解识别断层的应用中进行了初步试验，计算效率明显提高且取得良好的效果。

自适应核时频分析； 瞬时属性提取； 谱分解； 断层识别

0 引言

时频分析是从时间域和频率域两方面对信号进行描述，获取信号在时-频域的分布特征。传统的时频分析方法主要有：短时傅里叶变换、小波变换、S变换、魏格纳分布和Cohen类时-频分析[1]等。短时傅里叶变换、小波变换和S变换[2-4]属于线性时频分析方法，短时傅里叶变换受固定窗函数的影响，时间分辨率和频率分辨率相互制约[5]。S变换结合了傅里叶变换和小波变换，使信号的时频谱与傅里叶谱相关联，但是S变换的基函数固定，在应用方面受到一定地限制[6]。魏格纳分布[7]属于双线性时频分布，具有很高的时频分辨率，但是其存在严重的交叉项干扰，影响了信号有效时频谱地识别。Cohen给出了双线性时频分布一般的表示形式，在变换公式中加入了核函数来压制交叉项干扰的存在。但是不同的Cohen类时频分布核函数单一，对某一类型的信号有效，不具有普适性。针对上述问题，Baraniuk等[8]提出了径向高斯核时频分布，其核函数能自适应不同类型信号，但是对于同一类型信号，其信号特征随时间变化的情况不能够很好地解决。基于径向高斯核的自适应最优核时频分析方法(AOK)[9]解决了径向高斯核时频分布存在的问题，其核函数不仅可以适应不同类型的信号，而且可以随信号的变化而变化，具有局部自适应的能力。

我们对几种常用的时频分析方法进行对比分析，并探讨了自适应核时频分析方法，在瞬时属性提取和谱分解识别断层的应用效果。

1 方法原理

1.1 双线性时频分布

目前已知的双线性时频分析方法，都可以归结为Cohen类时频分布[1]。首先给出信号模糊函数的定义:

(1)

其中：s*(t)是s(t)的共轭函数;θ、τ是信号模糊域变量。

利用信号的模糊函数，得到信号s(t)的Cohen类双线性时频分布如式(2)。

e-jθt-jτωdθdτ

(2)

其中：P(t,ω) 是Cohen类时频谱；Φ(θ,τ)是信号s(t)的核函数。

从式(2)可以看出，信号的双线性时频分布，就是对信号的模糊函数加权再进行二维傅里叶变换得到的。通过设定不同形态的核函数Φ(θ,τ)，使信号模糊函数的自项能量也就是反映信号特征的有效能量通过，压制交叉项的干扰。

当设定核函数Φ(θ,τ)=1时，Cohen类时频分布就变成了魏格纳时频分布，由于没有对信号的交叉项干扰进行压制，因此，魏格纳时频分布存在严重的交叉项干扰。

1.2 自适应核时频分布

自适应核时频分布采用短时模糊函数和随时间变化的核函数[10]，即给信号加一个短时窗函数，在窗函数内部计算信号的模糊函数，同时在该时窗内计算最优的核函数，以达到核函数随信号的变化而变化的目的。

首先给出信号短时模糊函数的定义:

(3)

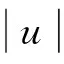
自适应核时频分布的定义，如式(4)。

Φopt(t;θ,τ)e-jθt-jτωdθdτ

(4)

其中：Φopt(t;θ,τ)是给定窗函数内的最优核函数；ω是频率变量；Φopt(t;θ,τ)是通过求解式(5)最优化问题得到的。

(5)

最优化问题的约束条件为

(6)

(7)

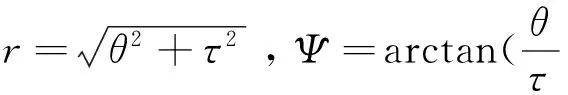
1.3 自适应核实现算法

最优核函数的快速计算需要在极坐标下完成[10]，计算过程需要用到极坐标下的短时模糊函数，其离散表达式为

bΔrsinqΔΨ

(8)

其中：Δr和ΔΨ是极坐标半径和角度变量的步长；b=0、1、…、B-1;q=0、1、…、Q-1。

核函数极坐标下离散表达式为式(9)。

(9)

其中：σq是控制核函数的形状的扩展因子。

σq=σ(qΔΨ)q=0,1,…，Q-1

(10)

计算最优核函数的过程，即计算最优扩展因子的过程，利用最速上升法来实现。计算步骤如式(11)和式(12)所示。

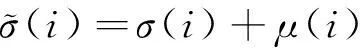
(11)

(12)

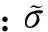
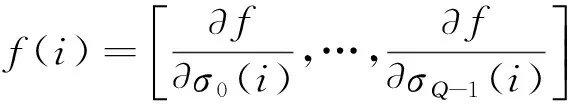
(13)

(14)

将式(13)和式(14)计算的结果代入式(11)，计算出最优的核函数和短时模糊函数之后，利用式(4)的离散格式就可以计算自适应核时频谱了。具体步骤如下：

1)在直角坐标系中计算信号的短时模糊函数A(n;θ,τ)。

2)将A(n;θ,τ)转换到极坐标下表示得到Ap(n;b,q)。

3)利用式(11)～式(12)的迭代算法计算最优的短时核函数的扩展因子σ。

4)计算最优的核函数Φp(n;b,q)。

5)将Φp(n;b,q)转换到直角坐标，并与短时模糊函数A(n;θ,τ)相乘，然后做二维傅里叶变换得到自适应核时频谱。

1.4 自适应核参数

在实际应用过程中，自适应核时频分析有两个关键参数：①时窗宽度；②核函数体积。利用自适应核时频分析完成不同的分析任务时，时窗宽度的设定有一个大致的准则，进行瞬时属性提取、谱分解时，选择比较小的时窗宽度，增大信号时频谱的时间分辨率。经过前期大量的实际地震资料的试验和应用，得出时窗宽度在二分之一主周期和一个主周期(主频对应的周期)之间效果较好。

在自适应核时频分析算法中，核函数体积的大小没有明确规定，只是给出了核函数体积范围一般在1～5之间。根据大量地震资料的试验和应用，得到在进行瞬时属性提取、谱分解时，核函数体积对结果影响不是很大。考虑到计算过程尽量保持各频率分量的衰减比不变[12]，选择比较小的核函数体积。

1.5 改进的自适应核时频分析

自适应核时频分析方法在计算时频谱的过程中，在每个样点所在的数据段上，都需要计算一个最优的核函数，因此计算量比较大。特别是在谱分解及其他属性提取的计算过程中，需要对每个地震道都需要进行最优核函数的计算，降低了运算效率。由于地下界面的连续性，地震剖面相邻地震道之间具有很强的相关性。因此，在利用自适应核来进行谱分解和属性提取的过程中，可以考虑利用相邻地震道之间的相关性，来提高自适应核时频方法的计算效率。

基本思想是，以奇数道为一个组合(例如3道、5道)，然后计算中间地震道的时频谱，得到该道每个样点所在数据段最优的核函数。在计算相邻道时频谱时，直接使用中间道计算得到的最优的核函数。这样可以节省最优核函数的一些计算过程，提高了计算效率。特别是数据量比较大时，计算效果比较明显。

选取某二维地震剖面，并分别以3道和5道作为一个组合，采用改进前、后的自适应核时频分析方法计算单个组合的时频谱，并比较改进前、后的计算时间。计算参数分别为：时窗宽度为64个样点，核函数体积为“1”，最优核函数迭代次数分别为2和3，程序语言matlab，计算时间统计如表1所示。

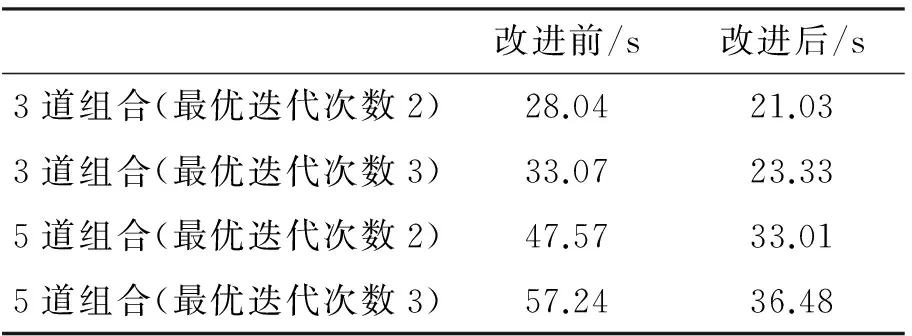
表1 改进前后自适应核时频分析计算时间对比Tab.1 Calculation time comparison of adaptivekernel time frequency analysis

从表1可以看出，随着组合内道数的增加，计算效率提高的越多。因此当地层起伏变化比较小时，可以适当增大同一个组合内的道数，当地层起伏比较大时，适当减小组合内道数。如果增加最优核迭代次数，改进的自适应核时频分析加速效果更加明显，一般情况下由于相邻样点最优核函数变化不大，因此迭代次数一般为2次～3次即可。

2 自适应核时频分析的应用

2.1 几种时频分析方法对比

时频分析方法的时频谱聚焦性能可以通过线性调频信号进行检验，为此设计一个线性调频信号如式(15)所示。该信号是两个线性调频信号的和，两个信号的频率变化范围分别是0.5Hz～40Hz、0.5Hz～80Hz，随着时间的增大信号的瞬时频率逐渐增大，每个时间点的瞬时振幅是相同的。该信号长度为2s，采样间隔为1ms，图1为该线性调频信号。

y= sin(2π(0.5+10*t)*t)+

sin(2π(0.5+20*t)*t)

(15)

其中y是两个线性调频信号的和。

图2为采用不同的时频分析方法对线性调频信号进行时频分析的结果。由图2可以看出：魏格纳分布(图2(a))的两条时频谱能量线清晰，时频谱聚焦性好，但是存在严重的交叉项干扰，影响了有效时频谱的识别；高斯小波变换(图2(b))的时频谱不存在交叉项干扰，随着信号频率的增大，信号的时频谱能量减小了，没有能够真实地反映信号的瞬时振幅特征；S变换(图2(c))能较好地反映信号的时频谱的变化规律，随着频率的变化信号的时频谱能量保持一致，但在高频端，S变换的时频谱的宽度明显增大，时频谱的聚焦度明显降低；自适应核时频分布(图2(d))采用最优的核函数压制交叉项干扰，同时保持高时频谱聚焦度，两条时频谱能量线清晰，能量变化反映了线性调频信号的特征。无论从聚焦度还是交叉项干扰的控制，自适应核时频分布都是理想的对非平稳信号进行分析的工具。

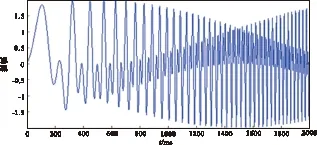
图1 线性调频信号Fig.1 The linear FM signal

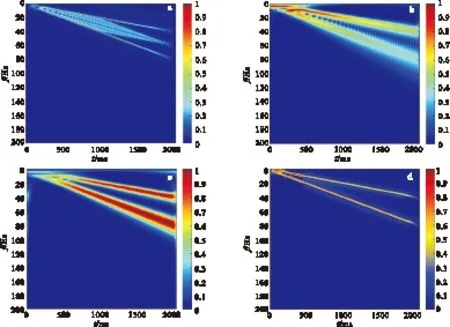
图2 不同时频分析方法的效果对比Fig.2 Result of different time-frequency analysis methods(a)魏格纳分布；(b)高斯小波变换；(c)S变换；(d)自适应核

2.2 瞬时属性参数提取

地震波在传播过程中，地震子波受到地层吸收、波前扩散和地层反射等影响，其频率、振幅和相位不断发生变化，并携带了大量的地下信息[10]，因此对地震记录瞬时属性的分析可以间接地反映地下地层的某些特性。利用地震瞬时属性的多属性联合解释技术[13]在实际应用(如储层预测[14]、地震相分析[15]、薄层厚度反演[16]以及频谱成像[17])中发挥了重要作用。利用自适应核时频分析方法可以提取地震记录的瞬时属性参数，并且相对于常用的小波变换有更高的时频谱分辨率。为了检验自适应核时频分析方法的实用性，选择某油田二维剖面进行分析，得到该剖面的瞬时属性剖面。该数据采样间隔为2ms，采样点为2 001，共有221道。选取时间段为1 000ms～2 500ms、145道～185道的部分地震数据进行瞬时属性提取，图3即为选取的二维剖面的局部。

从图4和图5可以看出：自适应核得到的瞬时属性和小波变换得到的结果形态相近，但分辨率要高于小波变换；图4(b)瞬时振幅剖面能量聚焦，相邻层的振幅能量界限更加明显；图5(b)瞬时频率的变化更清晰，层间关系明确。因此，自适应核时频分析可以用来计算地震记录的瞬时属性，而且提取的属性分辨率相对于常规的时频分析方法要高。

图3 地震记录Fig.3 Seismic record

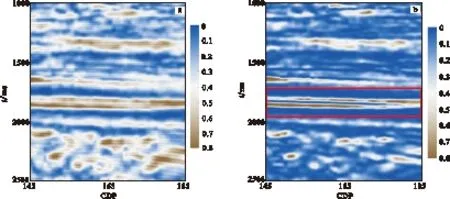
图4 瞬时振幅剖面Fig.4 The instantaneous amplitude profile(a)小波变换瞬时振幅；(b)自适应核瞬时振幅

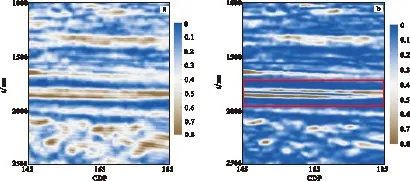
图5 瞬时频率剖面Fig.5 The instantaneous frequency profile(a)小波变换瞬时频率；(b)自适应核瞬时频率

2.3 谱分解识别断层

谱分解技术是利用时频分析将地震信号变换到时频域，提取某一频率的振幅信息作为分频剖面，然后利用不同的分频剖面，解释目的层的地质特征[18-19]。在实际应用中，可以利用谱分解分析确定断层的空间形态[20]。为了检验自适应核方法在断层识别方面的应用，利用自适应核时频分析对某二维剖面，提取其多个单一频率的振幅剖面，分析断层的形态。该数据采样间隔为2ms，采样点为3 000，共有593道。选取1道～151道的部分地震数据进行谱分解，图6(a)即为选取的二维剖面的局部。

从图6中的标注位置可以看出，340ms～390ms的断层，在原始地震剖面上很模糊，但是在不同频率的谱分解剖面上，断层的断点变清晰，尤其是50Hz剖面，断层的空间范围和断面位置很明确。

因此，对于断距比较小的断层，可以通过提取高于地震资料主频的频率切片来分析断层的形态特征。由于地震波存在吸收衰减，深部地层高频能量很弱，单纯依靠高频切片识别断层有一定的限制。因此可以利用自适应核谱分解技术得到不同频率的谱分解剖面，利用多个谱分解剖面综合识别地震剖面上不同深度的断层的空间形态。

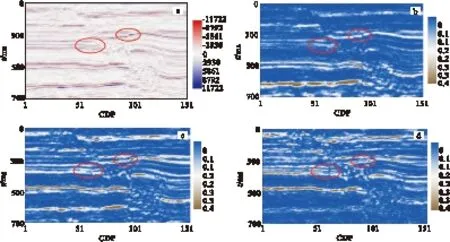
图6 原始地震剖面及不同频率的谱分解剖面Fig.6 Seismic record and spectral decomposition profiles of different frequency(a) 地震剖面；(b)10Hz；(c)30Hz；(d)50Hz

3 结束语

这里论述了自适应核时频分析方法的基本原理和计算的实现，并简单探讨了自适应核时频分析方法在瞬时属性提取和谱分解识别断层等方面的应用，得到以下结论。

1) 自适应核时频分析方法属于双性时频分布，相对于小波变换和S变换等线性时频分布，具有更高的时频分辨率；相对于魏格纳分布等Cohen类双线性时频分布，能够很好地压制交叉项干扰，精确地刻画非平稳信号的时频谱。

2)自适应核时频分析方法在属性提取方面，提取的瞬时属性具有比较高的聚焦度，层间界限明显；谱分解剖面识别断层，可以识别常规地震剖面不易识别的断层，高频切片在小断距断层的识别方面效果明显。

3)在地震剖面相邻道相似性的基础上，提出了改进的自适应核时频分析方法，提高了计算效率。

[1]COHENL.TimeFrequencyAnalysis:TheoryandApplication[M].EnglewoodCliffs,NJ:Prentice-Hall,1995.

[2] 马见青,李庆春.S变换和TT变换联合压制地震面波[J].物探化探计算技术,2011,33(3):252-25.MAJQ,LIQC.JointStransformationandTT-transformationmethodofsurfacewavesuppression[J].ComputingTechniquesforGeophysicalandGeochemicalExploration, 2011,33(3):252-257.(InChinese)

[3] 段俊,张白林,潘树林. 广义S变换去除面波技术及应用[J].物探化探计算技术,2011, 33(3):280-285.DUANJ,ZHANGBL,PANSL.GeneralizedS-transformanditsapplicationtoremovesurfacewave[J].ComputingTechniquesforGeophysicalandGeochemicalExploration, 2011, 33(3):280-285.(InChinese)

[4]HLAWATSCHF,BOUDREAUX-BARTELSGF.Linearandquadratictime-frequencysignalrepresentation[J].IEEESignalProcessingMag, 1992, 9(2): 21-67.

[5] 刘小龙,王华,赵淑娥,等. 自适应最优核时频分布在地震储层预测中的应用[J]. 中南大学学报(自然科学版), 2012,48(8): 3114-3120.LIUXL,WANGH,ZHAOSE,etal.Applicationofadaptiveoptimalkerneltime-frequencyrepresentationinreservoirprediction[J].JournalofCentralSouthUniversity(ScienceandTechnology), 2012, 48(8): 3114-3120.(InChinese)

[6] 刘喜武,年静波,黄文松. 利用广义S变换提取地震旋回的方法[J]. 石油物探, 2006,45(2): 129-133.LIUXW,NIANJB,HUANGWS.SeismiccyclesextractionusinggeneralizedS-transform[J].GeophysicalProspectingforPetroleum, 2006, 45(2):129-133.(InChinese)

[7] 刘喜武,刘婉莹,刘洪,等.地震信号广义时频分析及其数值实现[J].物探化探计算技术,2007, 29(5):386-390.LIUXW,LIUWY,LIUH,etal.Generalizedseismicsignaltime-frequencyanalysisandnumericalalgorithms[J].ComputingTechniquesforGeophysicalandGeochemicalExploration, 2007, 29(5):386-390.(InChinese)

[8]BARANIUKRG,JONESDL.Signal-dependenttime-frequencyanalysisusingaradiallyGaussiankernel[J].SignalProcessing,1993,32(3):263-284.

[9]JONESDL,BARANIUKRG.Anadaptiveoptimal-kerneltime-frequencyrepresentation[J].IEEETrans.onSignalProcessing,1995,43 (10):2361-2371.

[10]马成英. 时频属性提取方法及应用[D].青岛：中国海洋大学,2012.MACY.Time-frequencyattributesextractionmethodsandapplication[D].Qingdao:OceanUniversityofChina, 2012.(InChinese)

[11]BARANIUKRG,JONESDL.Asignal-dependenttime-frequencyrepresentation:optimalkerneldesign[J].IEEETrans.onSignalProcessing, 1993, 41 (4):1589-1602.

[12]张宇辉,金国彬,李天云. 基于自适应最优核时频分布理论的间谐波分析新方法[J]. 中国电机工程学报, 2006, 26(18): 84-89.ZHANGYH,JINGB,LITY.Anovelapproachtointerharmonicsanalysisbasedonadaptiveoptimalkerneltime-frequencydistribution[J].ProceedingsoftheCSEE, 2006, 26(18):84-89. (InChinese)

[13]周怀来,李录明. 广义S变换在地震信号特征信息提取中的应用[J]. 新疆石油地质,2008,29(6):758-760.ZHOUHL,LILM.ApplicationofgeneralizedS-transformtoextractionofseismicsignalcharacteristicinformation[J].XinjiangPetroleumGeology, 2008,29(6):758-760.(InChinese)

[14]刘其,赵永勤,窦慧媛,等. 利用地震波主参数预测岩性和油气[J]. 石油物探, 2003, 42(1): 77-81.LIUQ,ZHAOYQ,DOUHY,etal.Predictionoflithologyandhydrocarbonaccumulationwithseismicprincipalparameters[J].GeophysicalProspectingforPetroleum, 2003, 42(1):77-81.(InChinese)

[15]邹文,陈爱萍,贺振华,等. 基于S变换的地震相分析技术[J]. 石油物探,2006,45(1):48-51.ZOUW,CHENAP,HEZH,etal.SeismicfaciesanalysisbasedonS-transform[J].GeophysicalProspectingforPetroleum, 2006, 45(1):48-51.(InChinese)

[16]张显文,韩立国,王宇,等. 地震信号谱分解匹配追踪快速算法及其应用[J]. 石油物探,2010,49(1):1-6.ZHANGXW,HANLG,WANGY,etal.Seismicspectraldecompositionfastmatchingpursuitalgorithmanditsapplication[J].GeophysicalProspectingforPetroleum, 2010, 49(1):1-6.(InChinese)

[17]刘兰锋,曹思远,夏竹,等. 广义S变换及其在储集层频谱成像中的应用[J]. 新疆石油地质,2009,30(5):629-632.LIULF,CAOSY,XIAZ,etal.GeneralizedS-Transformanditsapplicationtoreservoirimagingbyenergyspectrum[J].XinjiangPetroleumGeology, 2009,30(5):629-632.(InChinese)

[18]尚帅,韩立国,胡玮,等. 压缩小波变换地震谱分解方法应用研究[J]. 石油物探,2015,54(1):51-55.SHANGS,HANLG,HUW,etal.Appliedresearchofsynchrosqueezingwavelettransforminseismicspectraldecompositionmethod[J].GeophysicalProspectingforPetroleum, 2015, 54(1):51-55.(InChinese)

[19]胡水清,韩大匡,刘文岭,等. 应用谱分解技术预测河道砂体[J]. 新疆石油地质,2008,29(3):370-372.HUSQ,HANDK,LIUWL,etal.Applicationofspectrumdecompositiontechniquetopredictionofriverchannelsands[J].XinjiangPetroleumGeology, 2008,29(3):370-372.(InChinese)

[20]张延庆,魏小东,王亚楠,等. 谱分解技术在QL油田小断层识别与解释中的应用[J]. 石油地球物理勘探, 2006, 41(5):584-586,591.ZHANGYQ,WEIXD,WANGYN,etal.ApplicationofspectrumfactorizationinrecognitionandinterpretationofminorfaultsinQLoilfield[J].OilGeophysicalProspecting, 2006, 41(5): 584-586,591.(InChinese)

Improvement of adaptive kernel time-frequency analysis and its application

YUE Long, LIU Huaishan, XU Xiugang

(Key Lab of Submarine Geosciences and Prospecting Techniques, Ministry of Education,Ocean University of China, Qingdao 266100,China)

Improving the seismic signal time-frequency resolution is the focus of time-frequency analysis research. The time-frequency resolution of the traditional linear time-frequency analysis methods, including short-time Fourier transform, wavelet transform and S transform is poor. Bilinear time-frequency analysis method such as Wigner distribution has a high time-frequency resolution but it is contaminated by serious cross-terms. Adaptive kernel time-frequency analysis belongs to bilinear time-frequency analysis. Under the premise of ensuring high resolution, it adopts the optimal kernel function changing with time to suppress cross-terms interference and improves the readability of time-frequency spectrum. This article compares the time-frequency spectrum of linear frequency modulated signal using for different methods. The adaptive kernel method has a better time-frequency concentration and been applied to real data and several tests have been carried out in instantaneous attributes extraction, fault identification using spectral factorization and sedimentary cycle analysis. The calculation effectiveness is improved and the results are satisfactory.

adaptive kernel time-frequency analysis; instantaneous attributes extraction; spectral factorization; fault identification

2015-12-30 改回日期：2016-03-01

国家自然科学基金(41176077，41230318，41204088);国家863 项目(2013AA092501);国土资源部海洋油气资源与环境地质重点实验室开放基金(MRE201303)

岳龙(1988-)，男，博士，主要从事地震勘探资料处理方法研究工作，E-mail: 957115928@qq.com。

1001-1749(2017)01-0044-08

P 631.4

A

10.3969/j.issn.1001-1749.2017.01.07