航空叶片非接触光学测量的转轴精密标定方法

何万涛，马鹤瑶，郭延艳，孟祥林

(1.华中科技大学 材料成型与模具技术国家重点实验室,武汉 430074;2.黑龙江科技大学 机械工程学院，哈尔滨150022; 3.黑龙江科技大学 工程训练与基础实验中心，哈尔滨150022)

航空叶片非接触光学测量的转轴精密标定方法

何万涛1，2，马鹤瑶3，郭延艳3，孟祥林2

(1.华中科技大学 材料成型与模具技术国家重点实验室,武汉 430074;2.黑龙江科技大学 机械工程学院，哈尔滨150022; 3.黑龙江科技大学 工程训练与基础实验中心，哈尔滨150022)

航空叶片为薄壁复杂扭曲件，转轴标定是获得完整叶片型面数据的前提条件，标定精度直接决定着最终获得叶片数据的整体精度。针对锥光偏振全息干涉的非接触式测头未进行路径规划前只能测量部分球冠点云、球心拟合精度不稳定的问题，提出了一种带半径约束的最小二乘球心拟合方法，通过八个方位扫描数据拟合球心与法线方向，实现转轴的精密标定。实验结果表明,该方法减小多方位测量点云分层效果显著，精度完全满足航空叶片的测量需求。

航空叶片；转轴标定；偏振全息干涉；半径约束

0 引 言

随着航空发动机涵道比、推重比及服役寿命的不断提高，对决定其能量转换效率的核心零件——叶片的设计制造提出了更高的要求。高性能叶片具有型面复杂、薄而扭曲、前后缘半径尺寸微小(最小直径0.1 mm)、制造检测精度要求高、数量庞大等技术特点[1]。在设计制造和安装调试过程中精度检测与控制至关重要。目前，光学三维测量法具有非接触、速度快、易于自动化，可以直接测量反光叶片零件表面，已经成为支撑叶片高水平设计、高精度制造和高可靠运行的关键技术之一[2-3]。然而，对复杂曲面叶片进行激光扫描三维测量往往需要对盆曲面、叶背曲面和前后缘曲面分别进行测量。多次不同方位、不同角度的测量才能获得完整的表面数据，所有不同方位测量的数据片组合成完整的被测物体外表面的过程称为多视拼合[4]。目前，常用的多视拼合方法有三类：一类是通过在被测量物体表面粘贴标记点，然后通过提取标记点的圆心或者角点等特征，获得两片数据点云对应的三个以上不共线点，通过这些点计算旋转矩阵和平移向量实现多视数据的拼合[5-7]；另一类是对数据点云的特征进行分析和提取，直接利用点云自身具备的特征进行匹配，学者们提出了各种特征提取算法，利用特征进行初步定位，然后应用ICP (Interactive closest point) 等算法进行优化[8-9]；第三类是通过标定测量头和旋转硬件装置的坐标位置关系，直接实现多角度点云数据拼合[10-13]。在拼合过程中应用哪种方法，要根据被测量零件的需求，设备的特点及条件。由于测量过程中产生各种误差和特征提取不准确等影响，无论采用什么方法拼合，多个视角测量点云都很难实现无缝衔接。而且多个视角数据整合到一起，误差累计造成整体拼合精度低于单次测量精度。通过不断改进硬件系统，优化数据拼接算法，进而提高拼合的精度与效率是非常必要的。文中根据所开发的四轴非接触测量设备的特点与航空叶片测量的需求，提出了一种转轴标定方法与技术方案，以期实现叶片多个不同角度下测量数据高精度、高效率的数据拼合。

1 球心拟合算法

文中所采用的锥光偏振全息干涉激光测距传感器由于测量景深和测量原理的限制，在未进行坐标系配准前只能通过盲扫描的方式获取标准球的部分球冠数据，获得的数据如图1所示。通过球冠进行球心拟合时，球心位置在某一方向上会出现一定的偏差，这个偏差会导致转轴标定结果的轴心位置误差。通过研究与实践，文中提出一种带半径约束的球心拟合算法。

图1 盲扫描获得的球冠数据Fig.1 Obtained part of spherical data without path planning

全息干涉扫描测量得到部分球面的三维坐标数据(xi,yi,zi)(i=1,2,…，n)，空间球面方程为

(x-a0)2+(y-b0)2+(z-c0)2=r2，

其中，a0、b0、c0为球心的坐标值，r为球的半径值，x、y、z是采用全息干涉测距传感器测量获取的三维球面点云的坐标值，将球面方程展开可以得到：

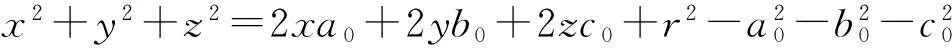
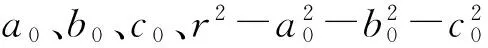
令

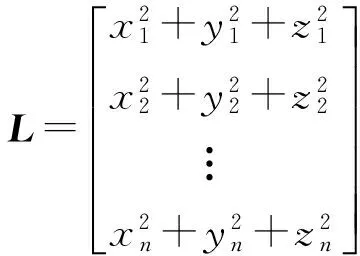
则矩阵L和A都含有误差的最小二乘模型为

最小二乘估计准则为

采用奇异值分解方法即可求出待估计的球心坐标值和半径。待拟合出球心值和半径后，将拟合得到的球半径和标准球的半径真值进行比较，误差如果在允许范围内(差值0.1 mm)，就强制将拟合值用半径真值代替，重新拟合获得球心值。实践表明这可以减小球心拟合偏差对标定精度的影响。

2 转轴标定方法

笔者开发的四轴非接触测量系统结构示意图如图2 所示。在互垂直的三个直线轴前面安装一个旋转轴，搭载激光测头组成四轴测量系统。由于叶片是薄壁复杂零件，通过360°旋转多视角测量才能获得完整数据，因此，转台中心轴线的标定精度会影响最终的测量精度。

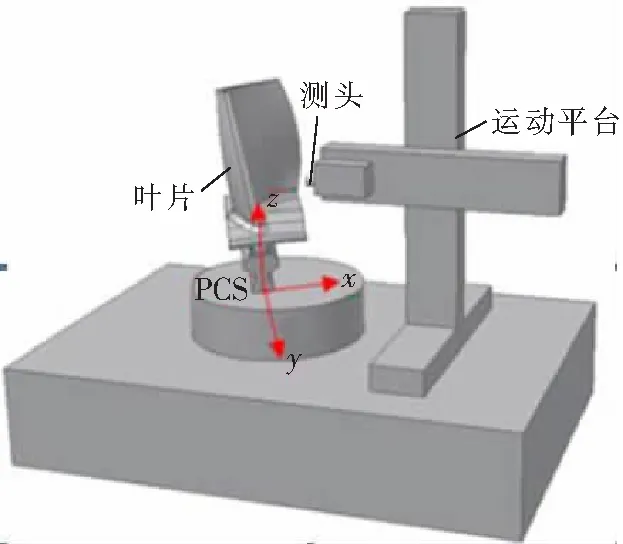
图2 四轴测量系统结构

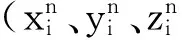
将这些球心坐标代入空间平面方程，构造线性方程组：

Axn+Byn+Czn+D=0，n=1,2,…，N。

利用最小二乘法求解该方程组，可以得到球心旋转轨迹所在的平面方程，该平面的法线矢量就是要求的转台转轴的法向矢量：

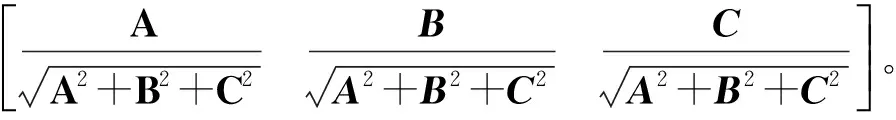
然后在轨迹平面内，利用搜寻算法求取与球心坐标On(xn,yn,zn)距离最小的点，即在约束条件

Ax+By+Cz+D=0,

的最小值，点OA(xA,yA,zA)可以认为是转轴与球心轨迹平面的交点，因此,该点也是转轴上的一点。

3 实验结果与分析

3.1 球心拟合结果对比

文中实验验证过程中对标准球进行测量，转台旋转45°采集一次标准球数据，采集标准球的所有球冠数据如图3所示。

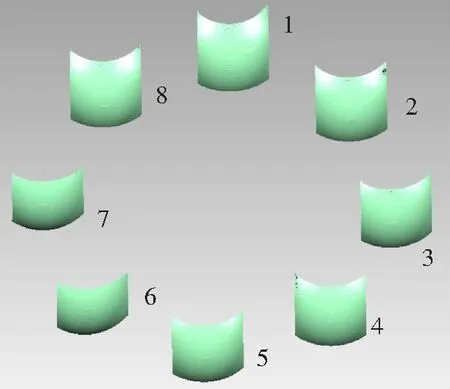
图3 测得的所有球冠数据

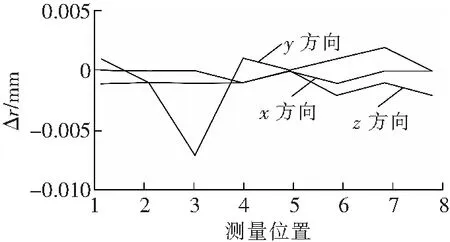
文中所采用的球心拟合算法用Matlab实现，对标准球进行数据采集八次，分别用带半径约束的拟合方法和不带半径约束的拟合方法进行比较分析，再将结果与Geomagic和Catia软件进行比较分析，分析结果见图4。

由图4结果可知，直接球心拟合结果与带半径约束的方法、Geomagic软件和Catia软件结果之间偏差主要来自于y方向的球心拟合误差。其主要原因可以从图5中看出，测量数据在y方向只涵盖很小一部分，因此拟合结果受数据影响大。而文中提出的带半径约束的方法与Geomagic软件、Catia软件结果之间偏差很小，满足文中标定精度的要求。

a 直接拟合法与文中方法比较

b Geomagic软件与文中方法比较

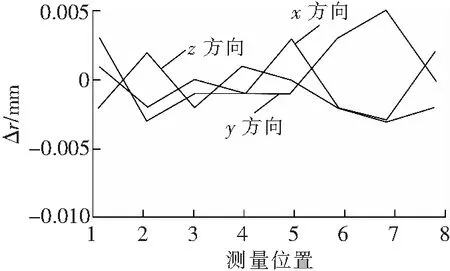
c Catia软件与文中方法比较

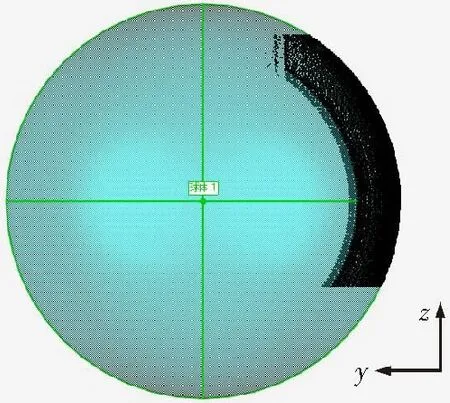
图5 球心拟合

3.2 精度分析

对标定球进行完整测量，应用上述球心数据及方法计算得到转台的中心点和转轴方向,对获得的球部分数据进行旋转和平移，最终获得完整的点云数据，具体过程及分析结果如下：

(1)在完成标定后，将标定球置于旋转台中心位置，分别对多次旋转前后的标定球表面进行测量；

(2)对测量结果进行球心拟合，拟合得到旋转前后的一系列球心坐标；

(3)根据旋转角度不同，将这些球心坐标分别绕轴旋转回初始位置，得到完整的球面数据。

(4)对球面数据进行分层切割，并对切割后的点进行圆拟合，得到拟合误差。拟合误差代表转轴标定的精度。

同时，可以得到标准偏差为0.01mm，从图6可以看出，精度整体保持在0.01mm水平。

图6 精度验证结果

3.3 叶片测量结果分析

文中前期的转轴标定中采取的方案是：

(1)在位置1对标准球进行测量，获得标准球的球冠数据；

(2)将标准球在精密转台上旋转180°后再进行一次球冠数据采集；

(3)对两个位置获得的球冠数据进行球心拟合，获得两个球心坐标；

(4)两圆心连线，计算线的中点为文中要求的转台圆心坐标；

(5)已该圆心为原点，默认z方向为法向就算转轴。

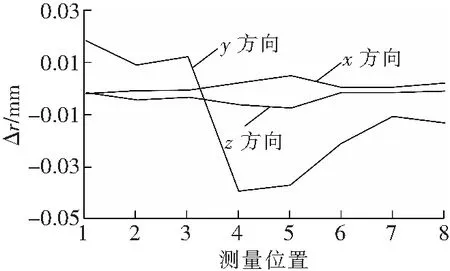
利用这种方法求取的转轴精度不高，对叶片进行实际测量中，数据会出现分层现象，测量数据结果见图7所示，从图7中可以看出，数据在前后缘部位有明显的分层现象，严重影响了测量精度。

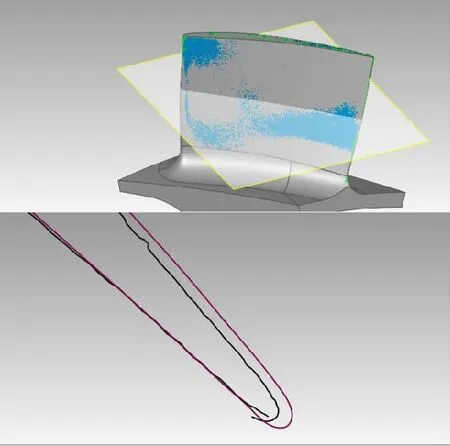
图7 前期方法测量结果

通过对全息干涉激光测头的特性进行分析，采用文中提出的标定方法后，测量精度有明显提升，效果如图8所示。

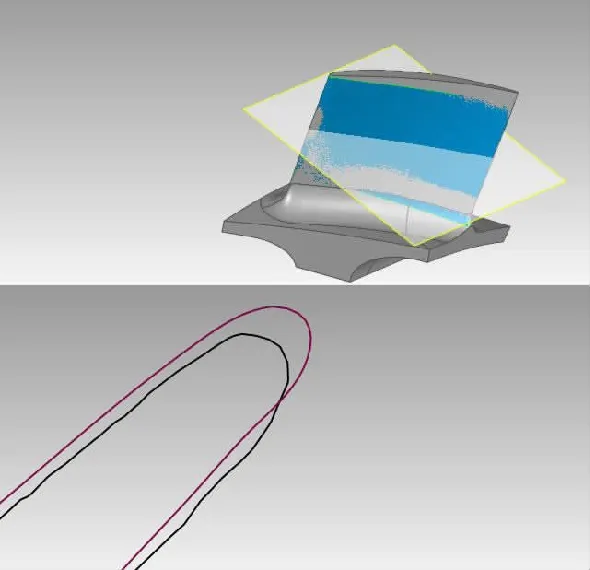
图8 文中方法的测量结果

4 结束语

综合考虑四轴光学精密测量系统的特点与航空叶片测量需求，提出了一种带半径约束的高精度球心拟合算法，实现了转轴的精确高效标定。对文中标定计算结果与业界领先的Geomagic、Catia三维处理软件计算结果进行详细对比分析，验证了文中提出方法的精度。同时，完成了精度验证实验，通过对标准球多视数据进行拼合，获得完整的球数据并对处理后的数据进行了截面分析，得出了转轴标定精度处于±0.01mm水平。进一步，通过实际测量验证了文中方法可有效减小数据的分层，完全满足航空叶片的精密检测需求。

[1] 李海宁,赵 赟,史耀耀,等.航空发动机风扇/压气机叶片制造关键技术[J].航空制造技术,2013，16: 34-37.

[2] 王淼安.光学测头在飞机发动机叶片检测中的应用[J].航空制造技术,2010(13): 32-35.

[3] 吴志新,韩 巍,黄 伟.非接触式白光测量机在叶片检测中的研究与应用[J].航空制造技术,2014,4(13): 48-51.

[4] Zhao H,Kruth J P,Gestel N V,et al.Automated dimensional inspection planning using the combination of laser scanner and tactile probe[J].Measurement,2012，45(5):1057-1066.

[5] Cuypers W.Gestel N V,Voet A,et al.Bleys Optical measurement techniques for mobile and large-scale dimensional metrology[J].Optics and Lasers in Engineering,2009,47(3): 292-300.

[6] 雷玉珍,李中伟,钟 凯,等.基于随机抽样一致算法的误匹配标志点校正方法[J].光学学报,2013,33(3): 205-212.

[7] 车向前,赵 灿,孟祥林,等.结构光测量系统中多视点云自动拼合算法[J].计算机应用,2008,28(6): 1514-1516.

[8] Diez Y,Martí J Salvi J.Hierarchical normal space sampling to speed up point cloud coarse matching[J].Pattern Recognition Letters,2012,33(16): 2127-2133.

[9] 黄欢欢,程 旭,钟 凯,等.旋转不变特征描述子的点云自动配准方法[J].黑龙江科技大学学报,2016,26(3): 316-322.

[10] 李 杨,许志闻,宋 展,等.面向全自动三维扫描系统的多视角三维数据自动配准技术[J].吉林大学学报: 理学版,2014,52(2): 319-325.

[11] 刘 飞,房建国,刘京亮,等.四轴坐标测量中转轴位置参数标定和数据整合[J].航空精密制造技术,2015(5): 20-23.

[12] 徐永安,杨 钦,怀进鹏.激光旋转扫描测量系统中转轴标定及多视拼合[J].中国激光,2005,32(5): 659-662.

[13] 冯 杭,张丽艳,王 兴,等.基于两轴数控转台的多视测量数据拼合[J].机械科学与技术,2012,31(2): 244-249.

[14] 袁 豹,岳东杰,赵元忆,等.基于稳健加权总体最小二乘法的地面三维激光扫描球型标靶定位[J].勘察科学技术,2013(1): 19-22.

(编校 王 冬)

Research on accurate calibration of shaft in non-contact optical measurement of aviation blades

HeWantao1，2，MaHeyao3，GuoYanyan3，MengXianglin2

(1.State Key Laboratory of Material Processing and Die & Mould Technology,Huazhong University of Science & Technology,Wuhan 430074,China；2.School of Mechanical Engineering,Heilongjiang University of Science & Technology,Harbin 150022,China；3.Center for Engineering Training & Basic Experimentation, Heilongjiang University of Science & Technology,Harbin 150022,China)

The blades are complex components that are twisted and thin-walled.Axis calibration presupposes complete blade surface data measurement and the calibration accuracy directly determines the overall accuracy of the blade measuring data.This paper is aimed at eliminating center fitting accuracy instability due to the little sphere data obtained using the conoscopic interference of non-contact probe before measurement path planning and presents a least squares fitting method with a spherical radius constraint.The research involves fitting sphere center and normal direction using eight azimuth scanning data to achieve accurate calibration of rotating shaft.The experimental results demonstrate that the method capable of a significant reduction in point cloud stratification provides the precision adequate for aviation blade measurement.

aviation blade；calibration shaft；conoscopic holographic interferometry；radius constraint

2017-02-23

国家自然科学基金项目(51505134)

何万涛(1981-)，男，黑龙江省哈尔滨人，工程师，博士研究生，研究方向：光学三维测量、机器视觉，E-mail：hewantao1225@163.com。

10.3969/j.issn.2095-7262.2017.02.018

TP391.41

2095-7262(2017)02-0181-05

A