塔机十字形基础的基底应力分析
2017-05-11李灿峰孙伟波
李灿峰,孙伟波
(浙江宝业建设集团有限公司,浙江 绍兴 312028)
塔机十字形基础的基底应力分析
李灿峰,孙伟波
(浙江宝业建设集团有限公司,浙江 绍兴 312028)
塔机十字形基础在硬土地区较为常用,它比矩形基础节约造价约20%。但十字形基础基底应力分布复杂,计算困难。今通过有限元建模分析十字形基础的基底应力分布规律,利用数学软件进行微积分计算,得到了精确、简便的计算方法,从而为塔机十字形基础的设计和施工提供了理论依据。
塔机;十字形基础;基底应力;有限元;微积分
塔机是建筑和市政工程竖向垂直运输能做到必备的施工设备。为保证塔机安装、使用的安全可靠,应选择科学、合理、经济的基础。在土质较好、地基承载力较高的地区,宜选择天然地基上的基础作为塔机基础,这样既能保证塔机的安全,加快工程进度,又能做到经济合理。天然地基上的塔机基础有矩形和十字形两种形式(图1)。十字形相对于矩形基础,承受相同荷载的条件下,能节约钢筋混凝土用量约20%,显示出了较好的经济效益。但十字形基础需要相对较大的施工作业空间[1]。

图1 塔机十字形基础
塔机十字形基础的基底应力分布十分复杂,采用常规的计算方式非常困难,国家行业标准《塔式起重机混凝土基础工程技术规程(JGJ/T 187—2009)》及各地省标如浙江省工程建设标准《固定式塔式起重机基础技术规程(DB33/T 1053—2008)》等均未提出相应的计算方法和公式。因此,目前工程上针对于塔机十字形基础的设计和施工,更多是依靠于相应的工程经验,通过对矩形基础的设计结果进行系数上的调整来实现。这完全偏离了塔机十字形基础基底应力分布的实际情况,存在严重的安全隐患,或过分加大了基础的规格尺寸,造成资源上的浪费和造价的增加。因此,根据塔机十字形基础的基底应力分布规律,制定出精确的、简便的计算模型和公式,是非常迫切的。
1 基底应力分布
塔机十字形基础在工作状态、非工作状态的荷载组合值差异较大,风荷载是起主要作用的影响因素。规定在六级强风时,塔机应停止工作,此时,基本风压为0.1 kN/m2(六级强风),在非工作状态时,如浙江省地区,50年一遇的基本风压可达到0.6 kN/m2(11级暴风)以上,两者相差6倍。同时,风荷载与塔机成45°角时,塔机的迎风面积达到最大,因此,在非工作状态下且按45°风向计算为最不利状态。下面通过有限元建模分析计算十字形基础基底应力的分布规律,十字形基础参数取值:a=2.6 m,b=1.0 m,c=3.3 m,h=1.0 m。N=600 kN,M=300 kN·m(按45°风向)。
1.1 有限元模型建立
采用Midas-GTS有限元分析软件建立塔机十字形基础的计算模型,土层取单一土层,采用摩尔-库仑模型,基础采用弹性模型,见图2。
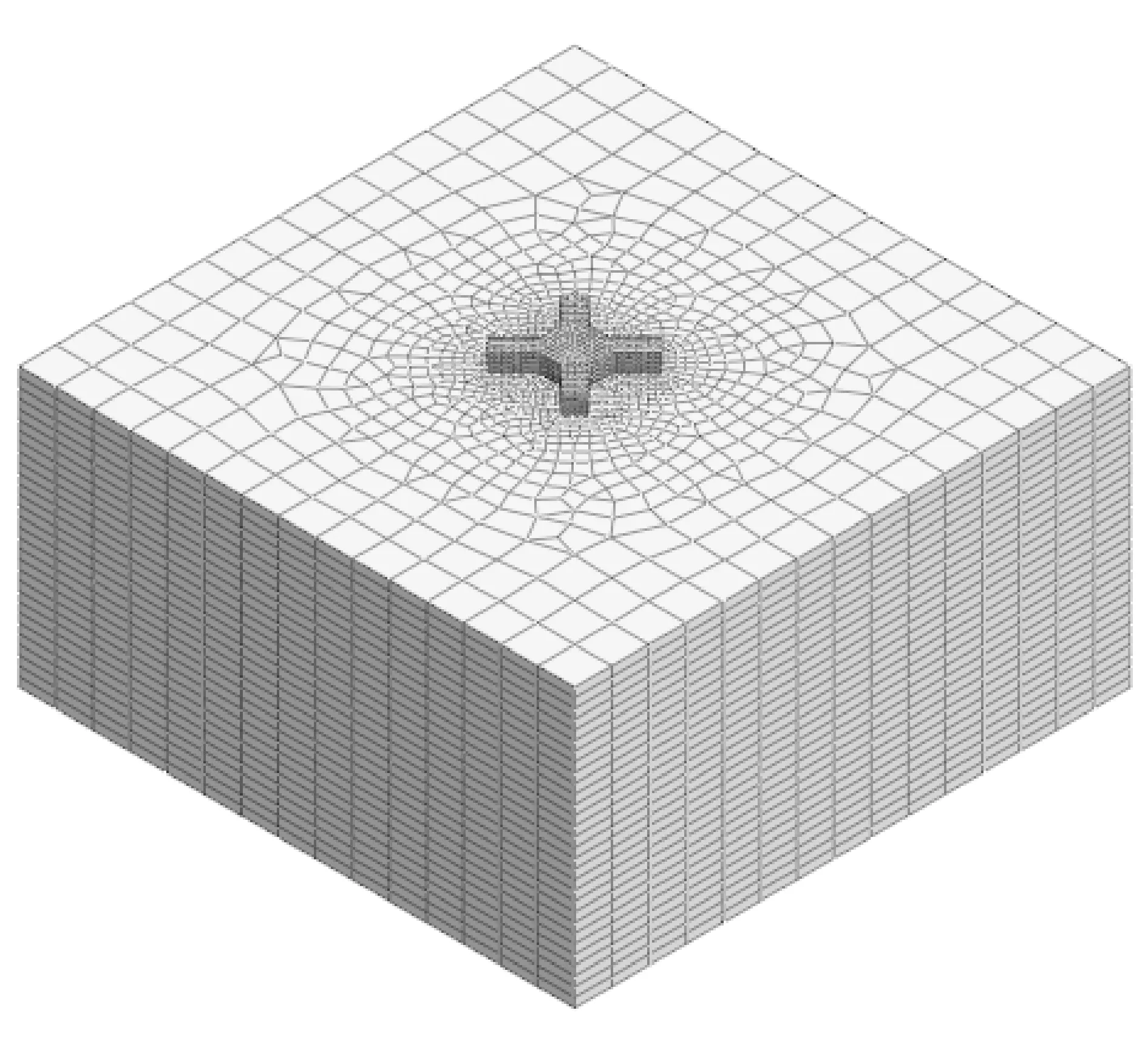
图2 有限元模型
1.2 有限元计算结果
将未添加塔机十字形基础的地基位移场设置为零,再计算基底的应力,有限元计算结果见图3。
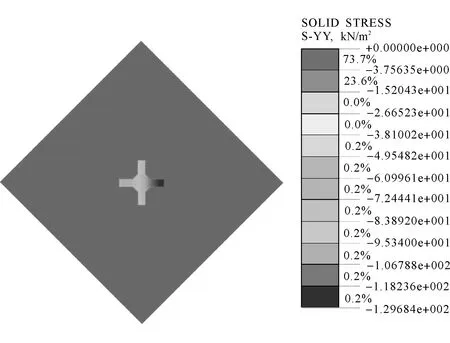
图3 基底应力分布
1.3 有限元计算结果分析
1)该计算结果远离偏心端(十字形基础左侧)地基应力不为零,为小偏心;若存在零应力区,则为大偏心。
2)塔机十字形基础的基底应力从远离偏心端沿十字梁长方向至偏心端(从十字形基础左侧至右侧颜色渐变,数值逐渐增大)逐渐增大,并呈线性分布。
2 计算模型
塔机十字形基础的基底应力可分大小偏心两种状态分别采用不同的方式进行计算。基础受力计算简图见图4。
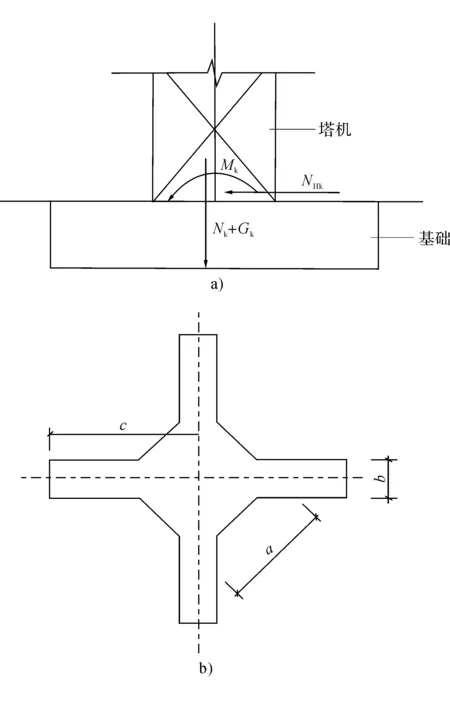
图4 塔机基础受力计算简图
图4中:Mk为作用于基础顶面的力矩标准值;VHk为作用于基础顶面的水平力标准值;Nk为作用于基础顶面的竖向力标准值;Gk为基础及基础上覆土的自重标准值[2-3]。
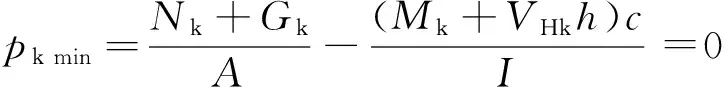
2.1 小偏心
小偏心计算简图见图5。
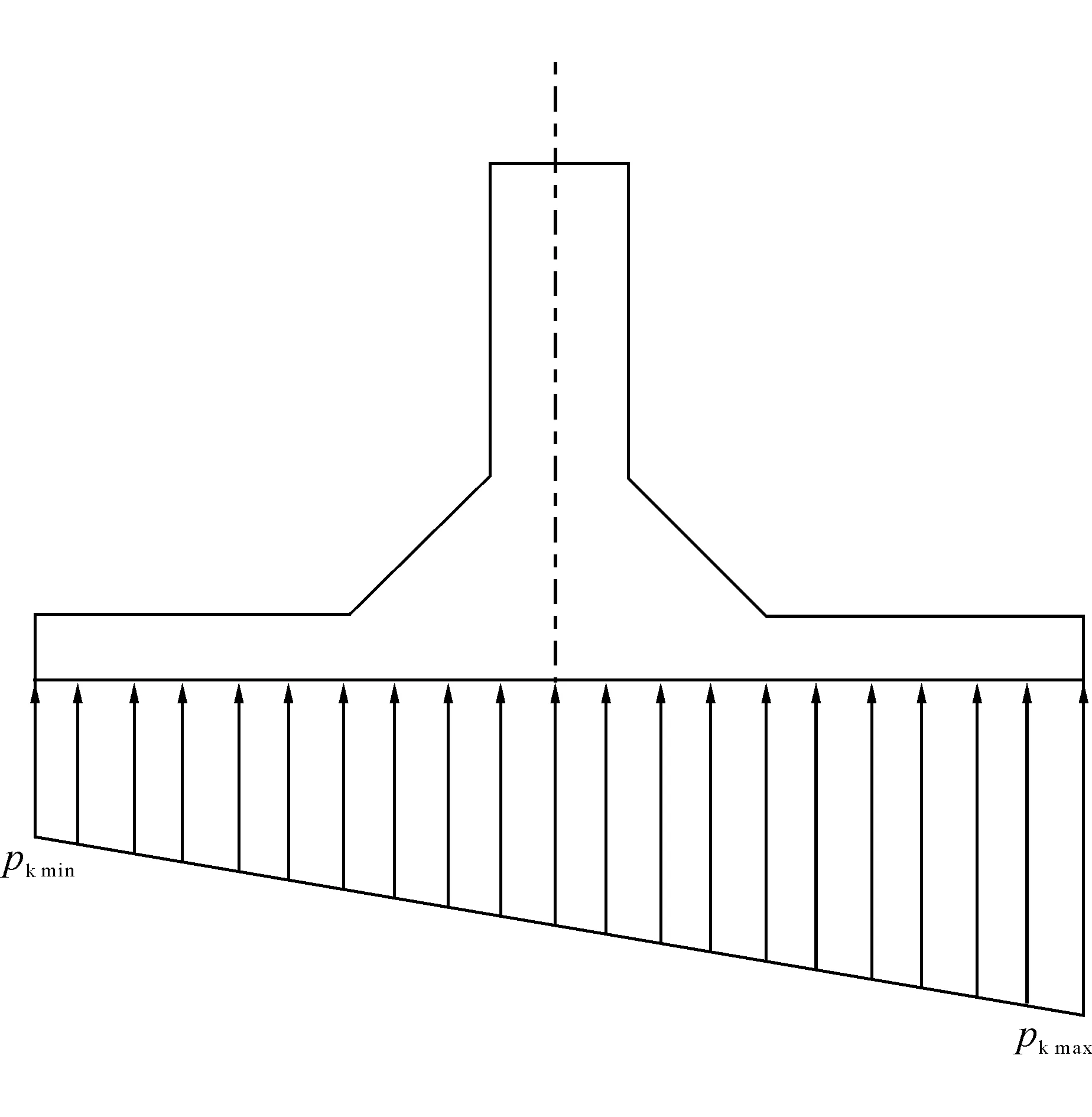
图5 小偏心计算简图
(1)
2.2 大偏心
2.2.1 计算模型
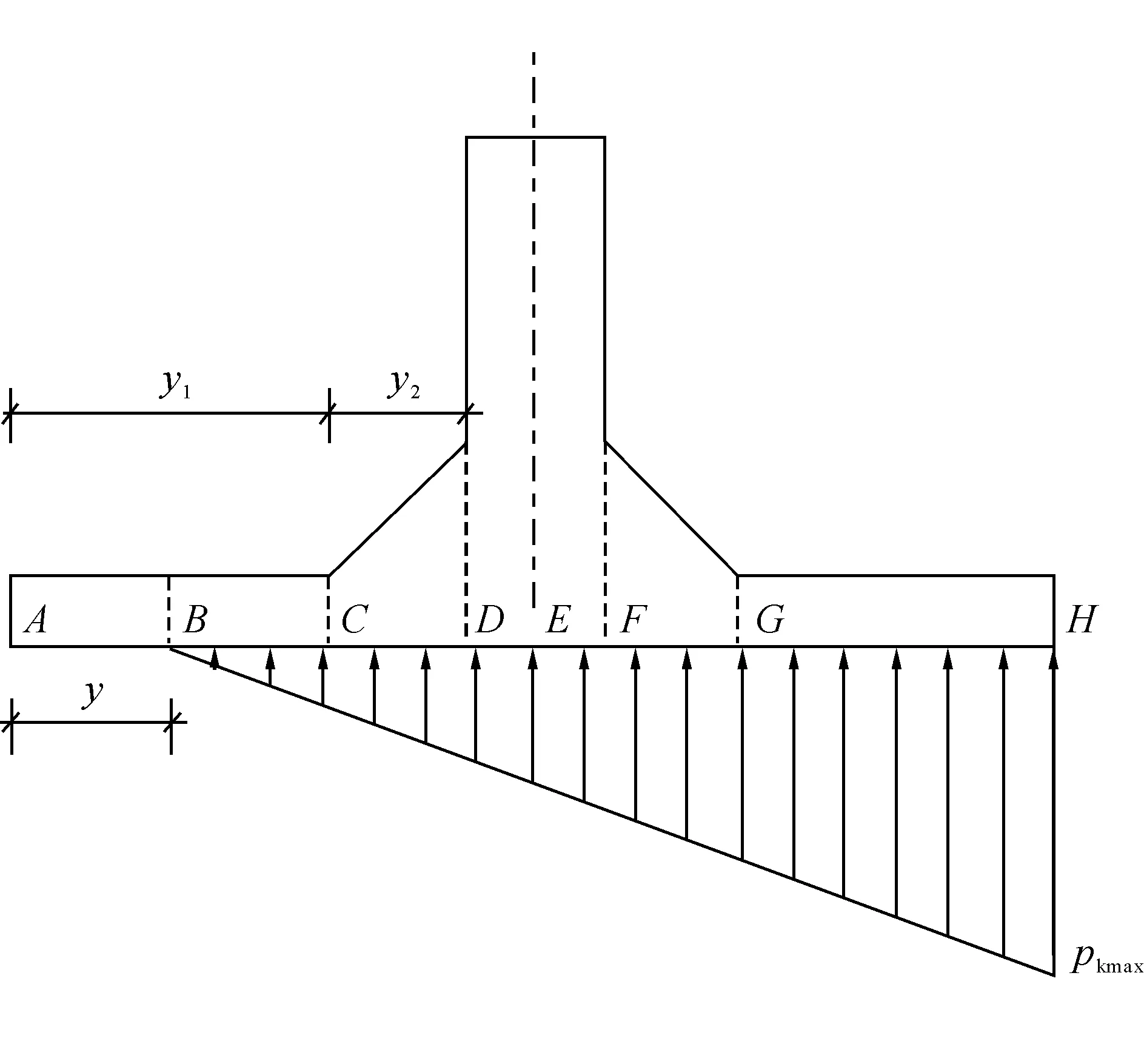
图6 大偏心计算简图
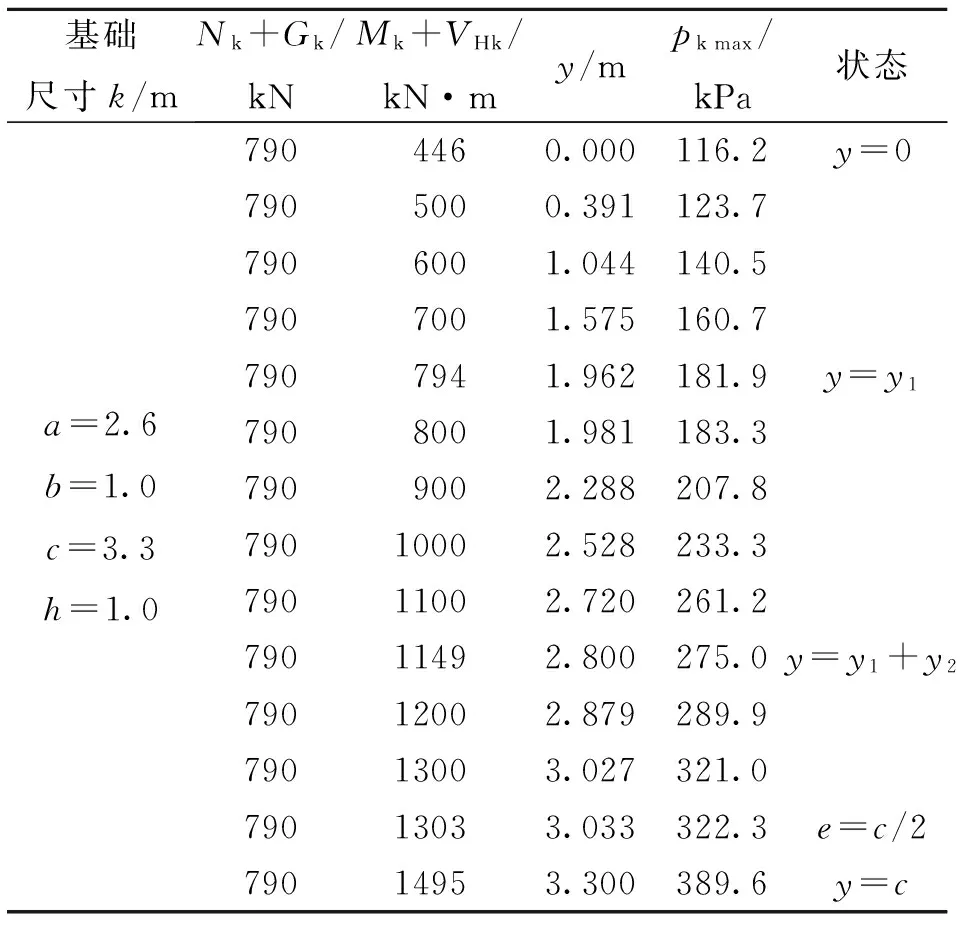
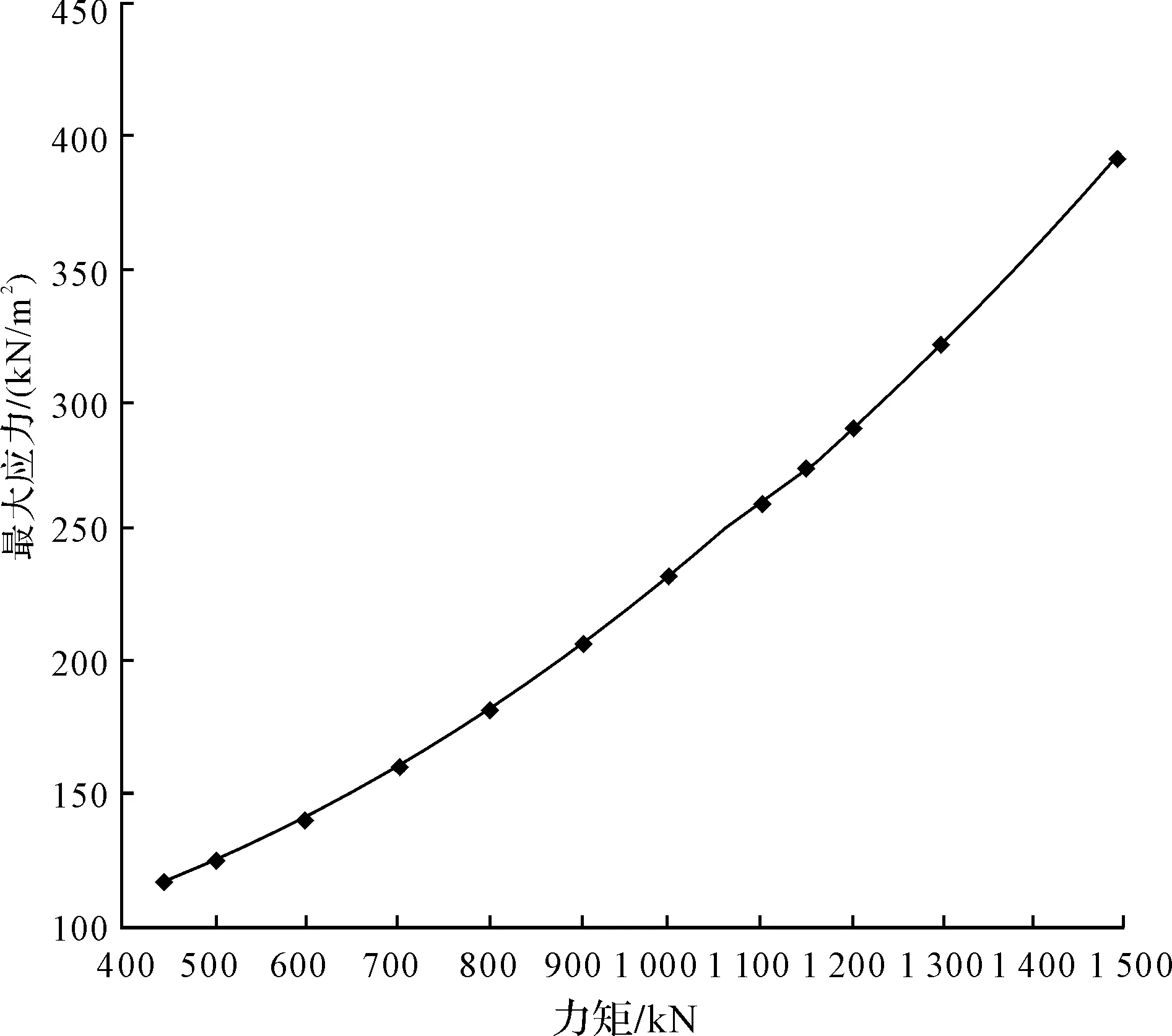
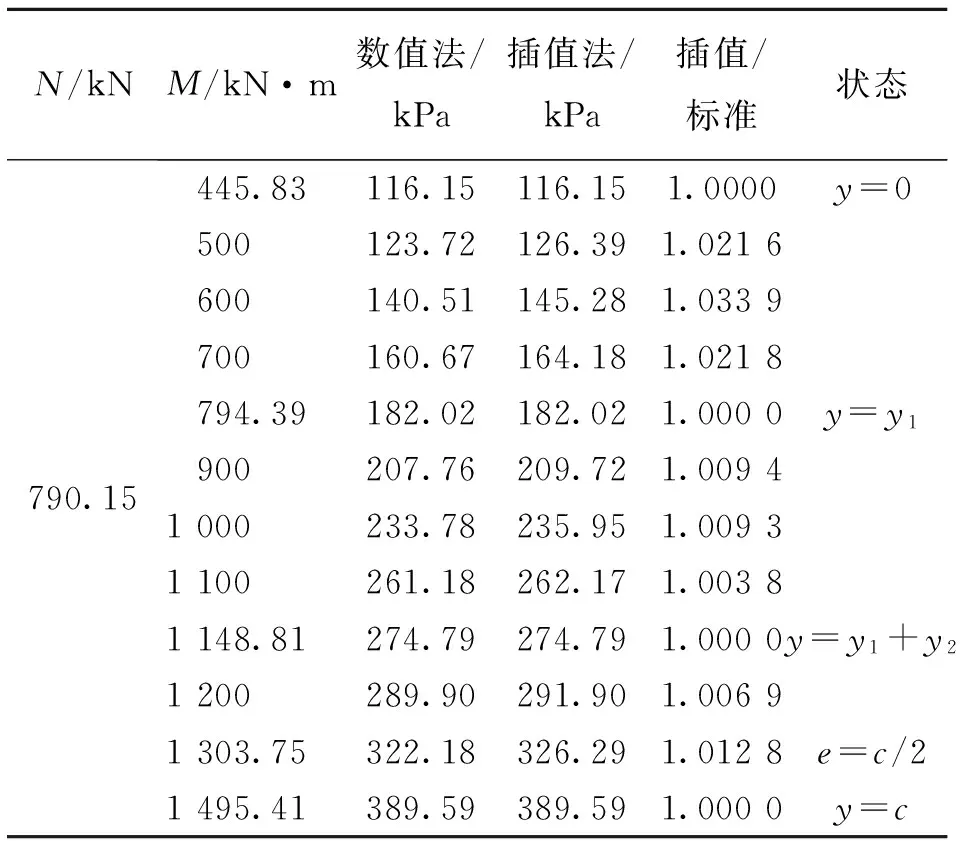
对A点积分,当0 连列得到二元方程组: 2.2.2 实例分析 对常用的塔机十字形基础进行实例分析,基础尺寸如下:a=2.6 m,b=1.0 m,c=3.3 m,h=1.0 m,当仅有Mk+VHk发生变化时,通过数学软件Mathcad求解方程组分别得到的解见表1和图7。 表1 实例计算结果表 从表1和图7中分析可知,塔机十字形天然基础梁边缘最大基底压力pk max与力矩Mk+VHk整体呈现正比例关系,曲线类似于平缓的二次方程,但在各特殊状态区段内基本成线性正比例关系;从另外的14组数据也验证了这一规律。因此,只要求出y=0、 y=y1、y=y1+y2、y=c等特殊状态时的pk max及相对应的力矩Mk+VHk,再根据力矩Mk+VHk按区段线性插值法计算即可获得任意状态下的pk max。 图7 实例计算结果图 3)得出公式 通过数学软件Mathcad求解y=0、y=y1、y=y1+y2、y=c等特殊状态时的pk max及相对应的力矩Mk+VHk计算公式,见表2。 表2 大偏心作用下十字形基础基底应力计算表 3.1 算例 下面通过举例说明塔机十字形基础基底应力的计算方法。某QTZ60塔机及塔基的设计参数如下:Nk=450 kN、Mk=868 kN·m、VHk=39 kN;a=2.6 m、b=1.0 m、c=3.3 m、h=1.0 m。将各参数代入表2,得到各特殊状态时的倾覆弯矩和基底最大压应力,见表3。 表3 QTZ60塔机十字形基础特殊状态的倾覆弯矩和基底压力 作用在基础底面的倾覆弯矩:Mk+VHk=868+39×1=907 kN·m,状态介于y=y1和y=y1+y2之间,用插值法解得: 3.2 数值比较 针对QTZ60塔机,采用上述方法的计算结果与采用微积分数值求解的方法比较,结果见表4。 表4 QTZ60塔机十字形基础基底应力计算结果表 根据表4分析可知,采用插值法计算得到的计算结果与采用微积分数值法的计算结果很接近,误差基本在3%以内;同时,结果计算略大,将实际的基底应力包络在内。因此,采用该种方法的设计结果完全能保证天然地基上塔机十字形基础设计所需要的精确性和安全性。 塔机十字形基础在土质较好的土层应用广泛,但基底应力分布复杂、计算困难,通过有限元分析和数值求解,得到以下结论: 1)基础在非工作状态下且按45°风向作用时为最不利状态。 2)基底应力从远离偏心端沿十字梁长方向至偏心端逐渐增大,并基本呈线性分布。 3)基底应力可按大小偏心分别采用不同的方法计算。 4)大偏心作用下,梁边缘最大基底压力与力矩在各特殊状态区段内基本成线性正比例关系。 5)采用区段插值方法计算的基底应力与实际应力分布误差可基本保证在3%以内。 天然地基上塔机基础采用十字形可比矩形节约造价约20%,但其基底应力计算一直是工程设计上的难题。通过有限元分析、数值求解归纳得到的区段插值法,能精确计算基底应力,从而为塔机十字形基础的设计和施工提供了简便的方法。 [1] 朱良锋,王国彦,张建良.十字形梁式塔机基础的设计计算[J].浙江建筑,2007,24(9):19-21. [2] 华丰建设股份有限公司.JGJ/T 187—2009塔式起重机混凝土基础工程技术规程[S].北京:中国建筑工业出版社,2009. [3] 浙江宝业建筑集团有限公司.DB33/T 1053—2008固定式塔式起重机基础技术规程[S].杭州:浙江省标准设计站,2008. [4] 王厚贞,周生玉,刘尊正.塔式起重机十字形基础的设计及校核计算[C]∥江苏省土木建筑学会建筑机械专业委员会学术年会.张家港:出版者不详,2011. [5] 何学功,冯功斌,孙刚.塔机十字形基础力学分析及抗倾翻稳定性计算[J].建筑机械,2001(1):27-30. Stress Analysis on Basement of the Cruciform Base for Tower Crane LICanfeng,SUNWeibo 2017-01-03 李灿峰(1984—),男,浙江绍兴人,工程师,从事建筑工程管理工作。 TU476+.1 B 1008-3707(2017)02-0034-05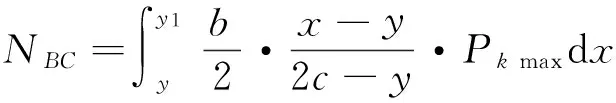
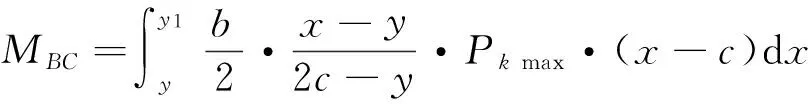
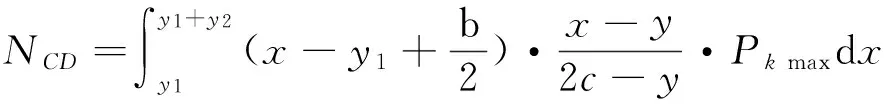
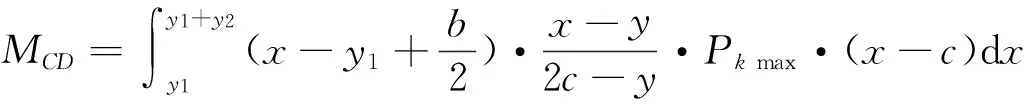
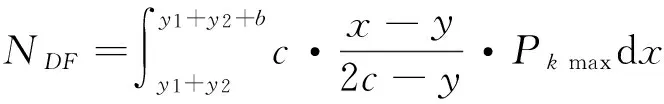
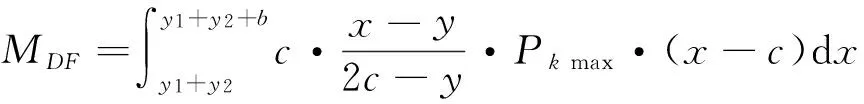
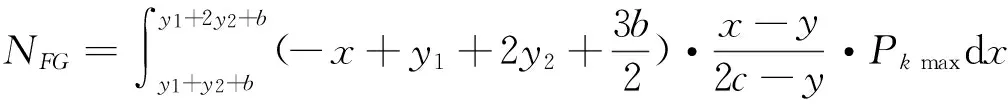
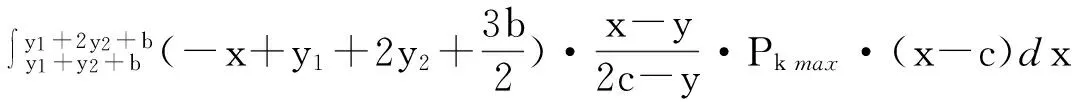
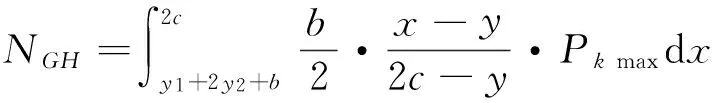
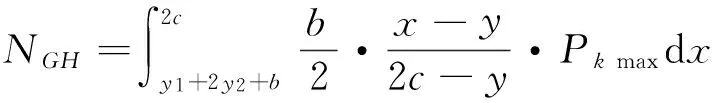
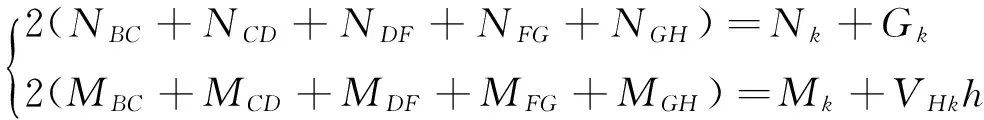
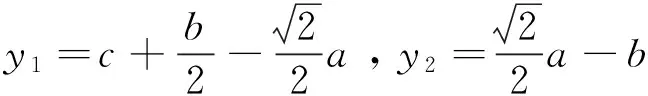

3 实例验证

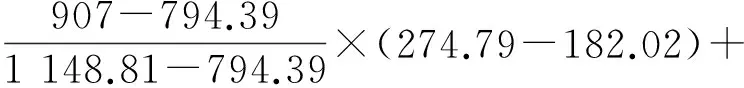
4 结 语
