多种群随机差分粒子群优化算法及其应用

王皓， 高立群， 欧阳海滨

(东北大学 信息科学与工程学院，辽宁 沈阳 110819)



多种群随机差分粒子群优化算法及其应用

王皓， 高立群， 欧阳海滨

(东北大学 信息科学与工程学院，辽宁 沈阳 110819)

为提高粒子群算法的寻优性能，提出了一种新的多种群随机差分粒子群优化算法。该方法将种群随机分组，利用基于吸引概率的轮盘赌方法确定其可能搜索方向。寻优效果预期不明显时，进行子种群内部随机差分进化寻优，以增加寻优方向的随机性和多样性。并给出了一种新的约束处理方法，对种群粒子进行动态划分，仅对部分粒子进行速度更新和位置更新，提高了搜索速度。并将所提出算法应用于数值优化问题和焊接梁设计问题。仿真结果表明，所提出算法在处理多峰函数问题时，寻优精度高，收敛速度快。在处理有约束问题时，提出的处理约束的方法，明显缩短了寻优时间。算法在处理复杂的无约束问题和有约束问题上均具有很好地寻优性能。

粒子群优化算法；多峰问题；约束优化；轮盘赌方法；差分进化；速度更新；位置更新；搜索速度；数值优化；焊接梁设计

粒子群优化算法(particle swarm optimization,PSO)是Kennedy和Eberhart于1995年提出的一种模拟鸟群社会行为的群体搜索算法。该算法简洁明了，具有良好的寻优性能，至今已广泛应用于科学、工程等许多领域。

随着对PSO算法及应用的不断深入研究，发现该算法和其他智能优化算法一样也存在着容易陷入局部最优问题。为提高其寻优性能，PSO算法不断改进，主要围绕三个方面：1)增加控制参数，通过引入惯性权重因子[1]、收缩因子[2]、被动聚集项[3]来防止粒子陷入局部最优；通过引入时变加速因子[4]来提高算法的效率和收敛速度。2)引入多种群协作[5]和动态种群概念[6]，通过多种群协作和种群的动态调整来提高算法的寻优能力。3)寻找有效的寻优策略，其研究主要集中在两条途径，一是引入随机进化[7-8]，二是对寻优策略进行自适应调整。至今PSO算法已得到深入研究，但陷入局部最优的问题仍然没能完全解决，还有进一步改进的空间。

鉴于工程实际中的优化问题往往需要满足各种要求和约束，如何处理约束也是优化研究的一个重要方向。不过由于利用罚函数法可以将约束问题转化为无约束问题，使得人们的研究更多地集中于无约束问题。后来发现，将无约束优化算法直接应用于约束问题时，寻优效果往往并不十分理想。为此，近年来人们提出了一些针对复杂约束的优化算法[9-10，15-20]，仿真结果表明这些算法对于很多复杂约束问题的寻优效果相当突出，得到了广泛认可。但是进一步研究可以发现，这些算法往往不能很好地解决多极值点的约束优化问题。因此，寻找一个能够很好地处理带有复杂约束的多极值点问题的算法具有一定理论意义和实际需求。

本文将多种群并行寻优与随机进化思想相结合，提出一种基于种群随机分组和随机差分策略的改进粒子群优化算法，同时给出了一种新的约束处理方法，并将该算法应用于焊接梁设计问题。

1 粒子群优化算法

一个由M粒子组成的群体在D维搜索空间中以一定的速度飞行，每个粒子在搜索时，根据自己搜索到的历史最好点和群体内其他粒子的历史最好点进行位置的变化。粒子的位置和速度更新公式：

xij(t+1)=xij(t)+vij(t+1)

(1)

c2r2j(t)[xbj(t)-xij(t)]，

i=1，2，…，M;j=1，2，…，D

(2)

2 多种群随机差分粒子群算法

人们在PSO算法研究中发现，通过两种途径可以克服算法陷入局部最优。一种途径是引入多种群协作[5]和动态种群概念[6]，可以使得粒子在寻优中不是单一以全局最好粒子作为寻优引导方向，而以一定概率分别向多个方向引导。寻优方向的多样性增加了寻优路径的多样性。另一种途径是不以某一个或几个确定的方向来引导粒子寻优，而是以一定概率在某些较好方向进行随机引导，增加了寻优路径的随机性，文献[11]提出了一种基于动态拓扑的粒子群算法。在算法前期，采用概率选择机制弱化全局最优粒子的影响力，以增强解的多样性，而在算法后期，强化全局最优粒子的影响力，最终能够收敛到一个最优解。本文将上述两种改进思想加以融合提出一种多种群随机差分粒子群算法，简记为MPPSO算法。

2.1 MPPSO算法的基本步骤

1) 初始化。

根据实际确定问题维数D，算法中的学习因子c1、c2，最大迭代次数N，子种群个数K及每一子种群内粒子个数。为简单起见，可取子种群中粒子个数均为m，则粒子总数为M=m×K。随机产生m×K个初始粒子xij(0)，i=1，2，…，m，j=1，2，…，K。计算粒子适应度值，针对每个粒子计算出相应的适应度函数值f(xij(0))。

2) 计算吸引概率。

在每组中基于目标函数值找出组内最优值和最优粒子以及全局目标函数最大值fmax。计算每个粒子受到各个小组最优粒子的吸引概率：

(3)

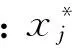
3) 产生新的粒子。

①对于每个粒子，基于受到各个小组最优粒子的吸引的概率pij(t)，利用轮盘赌的方法确定其可能搜索方向j，即可能向第j组的最优粒子方向搜索。

②b为变异参数，取随机数b=rand(0，1)，基于选择的搜索方向j，利用式(4)～(6)产生新的粒子的第s维分量。

(4)

(5)

s=1，2，…，D

式中：r1=rand(0，1)，r2=rand(-0.5，0.5)，c1、c2为学习因子，xrj为任意一个不等于xij的粒子。

(6)

4) 判断运算是否到达指定的最大迭代次数N，如果没有达到，则转向步骤2)；

5) 输出结果，程序结束。

2.2 MPPSO算法中的改进和特点

MPPSO算法对现有粒子群算法进行了改进，其改进和特点主要表现在以下几方面：

1)通过分组和吸引概率的引入增加粒子的寻优搜索方向。由于引导方向的多样性，可以增加粒子跳出局部最优的可能性，有利于解决多极值点问题。

3)在式(5)中，取参数r2=rand(-0.5，0.5)，使得迭代寻优中进行一定的反向搜索，有助于提高寻优效率。

4)寻优中根据贪婪原则确定新的粒子，可以保证算法的收敛性。

3 约束处理

实际优化问题通常情况下都含有约束，问题越复杂，约束就越多。一般约束优化问题的数学模型可表示为

minf(x)

s.t.gj(x)≤0j=1，2，…，ng

(7)

式中：f(x)表示目标函数，gj(x)表示第j个约束条件，ng为约束条件的个数。

对约束优化问题的求解，目前有许多算法——如梯度映射法、梯度下降法、惩罚函数法、障碍函数法等，其中处理约束问题最简单也是常见的方法是惩罚函数法，该方法通过惩罚策略将带有约束优化问题转化为无约束优化问题。

(8)

式中：λ为惩罚系数，本文中设置为1010。

在应用罚函数法处理约束问题时，在寻优的每一步通常都需要计算罚函数值，当约束较多、较复杂时，计算F(x)的时间要远远多于计算f(x)的时间，这大大增加了计算时间，降低了寻优效率。为解决这一问题，本文提出一种新的处理方法。此方法的特点是对种群进行动态划分，只有当无约束目标函数值小于已有可行解中的最差值时才考虑约束的限制，从而不需在搜索的每一步都计算惩罚函数值，提高了寻优效率。

为方便起见，将式(8)改写为

minF(x)=f+λf1

(9)

在第t+1代寻优中，首先计算f(x(t+1))的值，然后将其与上一代可行解中的最差值fworst(x*(t))=Fworst(x*(t))进行比较，如果f(x(t+1))≤Fworst(x*(t))，则计算惩罚函数值f1(x(t+1))，当f1(x(t+1))≤0时，取F(x(t+1))=f(x(t+1))，进入下一步寻优；当f1(x(t+1))>0时，取F(x(t+1))=f(x(t+1))+λf1(x(t+1))。如果f(x(t+1))>Fworst(x*t)，则直接进入下一代寻优。记Fg(t)=max{F(xi(t))|i=1，2，…，m×K}，针对约束问题，计算吸引概率的式(3)应改写为

(10)

此方法只是对具有较好f值的解进行有关约束的计算，利用惩罚策略使其向可行解空间移动，而不是对每一个解都进行约束计算，因此可以大大提高寻优速度。

注意这里的较好f值的判断是根据可行解中最差解所做出的，当然也可以根据其他准则给出判断。判断准则的好坏会直接影响寻优效果。比如：若采取基于可行解中最好解的准则，则限制过于苛刻，使得仅有极少数粒子参与更新(寻优)，会严重影响寻优效果；若采取基于所有解中最差解的准则，则限制过于宽松，不能明显地缩短寻优时间。

上述处理方法的具体实现步骤如下：

1)算法初始化。令循环变量t=1，随机产生若干个初始解向量，对采用的相关启发式优化算法进行参数设置；根据式(9)计算无约束目标函数值f(x(t))和惩罚函数值f1(x(t))。当f1(x(t))=0时，所对应的解为可行解，保存可行解中的目标函数最优值fbest(x*(t))及对应的最优可行解x*(t)。保存可行解中的目标函数最差值fworst(x*(t))=Fworst(x*(t))，若没有可行解，则重新初始化，直至找到可行解。

2)根据式(10)计算吸引概率。

3)根据式(4)、(5) 对粒子进行速度更新和位置更新。

(11)

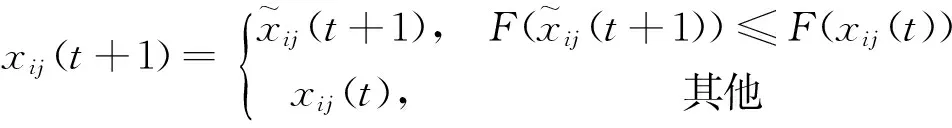
(12)

并保存F(x(t+1))，Fbest(x*(t+1))和Fworst(x*(t+1))。

6)判断迭代次数是否达到预先设置的最大迭

代次数，如果达到，则输出最优解，停止迭代；否则重复步骤2)～5)。

4 数值仿真实验

4.1 无约束优化

现行各类算法对于单峰函数的寻优效果相差不多，都比较好，而且本文算法主要是解决多峰函数优化问题，因此实验中选取了参考文献[12]所列举的多峰函数及文献[13]的Enhanced Bat Algorithm作为测试函数，具体如表1所示。对算法MPPSO进行测试比较主要基于以下几个性能指标：算法参数的影响、优化精度即最终解的质量和收敛速度。

算法参数设置：种群规模20，每组粒子5，共4组，学习因子c1=c2=1.7，维度D=30，算法独立运行30次。各类算法的迭代次数均为50 000次。

4.1.1 算法参数的影响

在式(5)中引入变异参数b。当参数b取不同值时的测试结果如表2所示。由表2可知当b=rand(0，1)时，既增加了寻优方向的随机性和多样性，又很好的解决了陷入局部最优的问题。图1给出6个函数在不同变异参数b下的优化曲线。

表1 无约束测试函数

表2 测试结果比较

图1 6个函数的收敛曲线(MPPSO)Fig.1 Convergence curves of 6 functions(MPPSO)

函数GPSOFIPSHPSO-TVACCLPSOAPSOEBAMPPSOf1Mean-9845.27-10113.80-10868.57-12557.65-12569.5-6.98×103-12569.50S.D588.87889.5828936.205.22×10-119.61×1020f2Mean69.0629.982.392.57×10-115.80×10-153.44×1010S.D8.0710.923.716.64×10-111.01×10-141.28×1010f3Mean21.3335.911.830.174.14×10-16-0S.D9.469.492.650.381.45×10-15-0f4Mean1.40×10-147.69×10-152.06×10-102.01×10-121.11×10-144.58×10-14.44×10-15S.D3.48×10-159.33×10-169.45×10-109.22×10-133.55×10-155.78×10-11.95×10-15f5Mean1.31×10-29.04×10-41.07×10-26.45×10-131.67×10-27.30×10-30S.D1.35×10-22.78×10-31.14×10-22.07×10-122.41×10-29.46×10-30f6Mean3.46×10-31.22×10-317.07×10-301.59×10-213.76×10-319.99×10-10S.D1.89×10-24.85×10-324.05×10-301.93×10-211.20×10-301.840

4.1.2 优化精度比较

在本小节中，利用表1所列举的6个测试函数测试算法的寻优能力即最终解的质量，与文献[12-13]所列各种近期典型算法优化测试比较结果如表3所示。

从表3的结果可以看出，本文算法对于无约束多峰函数f1～f6都具有很好的寻优效果。其原因是通过分组和吸引概率的引入增加粒子的寻优搜索方向。由于引导方向的多样性，可以增加粒子跳出局部最优的可能性。式(5)中引入变异参数b，取随机数b=rand(0，1)，既增加了寻优方向的随机性和多样性，又很好的解决了陷入局部最优的问题。因此在解决多峰函数问题时具有较好的效果。

4.1.3 收敛速度

图2显示出MPPSO算法在迭代过程中具有稳定的收敛率并且能够快速寻找到最优值。MPPSO算法函数f1、f4、f5、f6中具有较好的收敛率，在函数f2、f3中虽然收敛不是最快，但是寻优效果好。

4.2有约束优化

参数设置：种群规模100，每组粒子25，共4组，学习因子c1=c2=1.7，最大迭代次数50 000，维度D=30，算法独立运行30次。为测试本文提出的算法的有效性，本文采用了两类测试函数。一类来自于文献[14]中的测试函数，这类函数的特点在于所具有的约束比较复杂，使得通常对无约束问题有着很好寻优效果的算法，对于这类约束问题往往寻优效果可能并不理想，因此文献[14]给出了适用于复杂约束问题的算法。另一类是对于前面的无约束多峰函数分别加上一定约束所构造的测试函数，其特点在于目标函数多峰，使得目前处理约束问题较好的算法在寻优中效果可能会收到影响。由于篇幅所限，在两类函数中下面仅列出对比效果比较明显的9个测试函数，其中g01、g02、g04、g06、g08和g12来自文献[14]；h01、h02、h03是本文在无约束多峰测试函数基础上增添约束所构造的，其构造目的在于检验算法对带有约束的多峰测试效果。自定义的测试函数具体形式如表4所示。

与目前人们认为处理约束问题较好的算法FSA[15]、MicroPSO[16]、CW[17]、CMODE[18]、MHS[19]进行比较，这些算法的参数都根据算法发表的文献进行设置，针对约束分别采用常规罚函数法和本文提出的处理方法，所用时间对比见表5，由表5可知本文提出的处理约束的方法能够明显缩短寻优时间。

从表6的结果可以看出，本文提出的改进算法对函数g01、g02、g04、g06、g08、g12、h01、h02、h03都有很好的寻优效果，都能找到最优值，明显优于FSA、MicroPSO、CW、CMODE、MHS算法。其中CMOD算法寻优性能也比较好，对函数g01、g04、g06、g08、g12上也可以找到最优值，但是对于函数g02、h02、h03的寻优上效果不佳。

5 在焊接梁设计问题中的应用

为进一步验证本文算法的有效性，下面将本文算法应用于焊接梁设计问题。参数设置：种群规模100，每组粒子25，共4组，学习因子c1=c2=1.7，最大迭代次数20 000次。

焊接梁设计问题是指在受剪应力、弯曲应力、屈曲载荷、结尾偏差和侧面限制约束的限制下找到最低的制造成本[20]。数学模型如文献[20]所示。

图2 收敛曲线Fig.2 Convergence curves

问题测试函数维数h01minf(x)=-∑ni=0xisin(xis.t.g1(x)=2x1+2x2+x10+x11-10≤0,g2(x)=2x1+2x3+x10+x12-10≤0,g3(x)=2x2+2x3+x11+x12-10≤0;g4(x)=-8x1+x10≤0,g5(x)=-8x2+x11≤0,g6(x)=-8x3+x12≤0,g7(x)=-2x4-x5+x10≤0,g8(x)=-2x6-x7+x11≤0,g9(x)=-2x8-x9+x12≤0,g10(x)=∑ni=0x2i-n≤0,-500≤xi≤500(i=1,2,…,13)ìîíïïïïïïïïïï13h02minf(x)=14000∑ni=1xi2-∏ni=1cosxiiæèçöø÷+1s.t.g1(x)=∑ni=1xi+∏ni=1xi-100≤0-600≤xi≤600,i=1,2,…,20ìîíïïïï20h03minf(x)=πn{10sin2π+π4(x1-1)()+∑n-1i=118(xi-1)21+10sin2π+π4(xi+1-1)()[]+18(xn-1)2}+∑ni=1u(xi,10,100,4)u(xi,a,k,m)=k(xi-a)m, xi>a,0, -a≤xi≤a,k(-xi-a)m, xi<-a.{s.t. g1(x)=127-2x12-3x24-x3-4x42-5x5≥0,g2(x)=282-7x1-3x2-10x32-x4+x5≥0,g3(x)=196-23x1-x22-6x62+8x7≥0,g4(x)=-4x12-x22+3x1x2-2x32-5x6+11x7≥0,-10≤xi≤10, i=1,2,…,7ìîíïïïïïïïïïïïïïï7

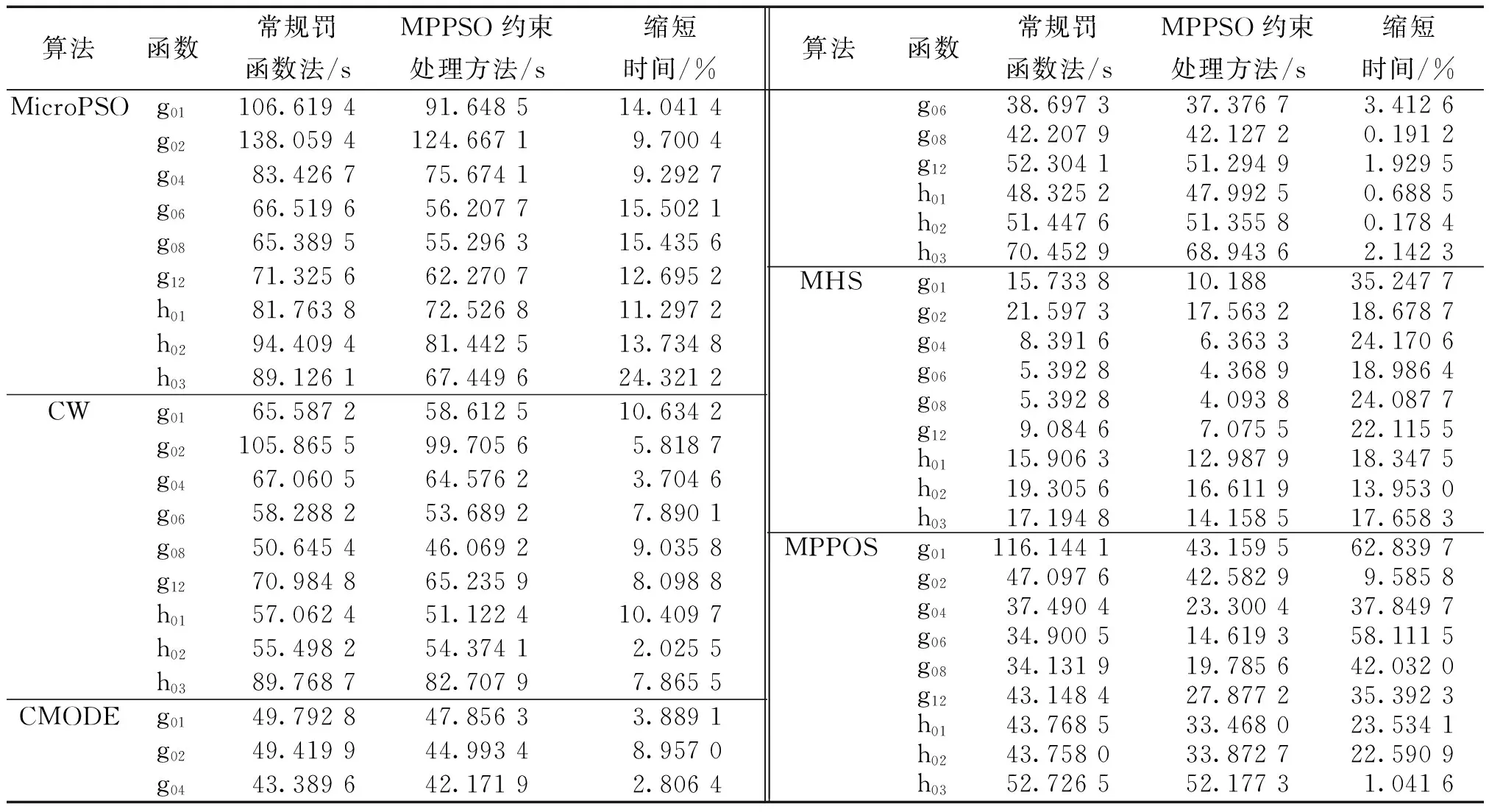
表5 寻优时间对比结果

表6 实验结果

在Zou[20]文章中提出最优解f(x*)=1.695 266 99，表7为Zou[20]和其他研究者与本算法解决此问题的近似最优解比较。从表7中可看出，本文得出的近似最优解f(x*)=1.593 181 44，明显优于其他所有算法的近似最优解，同时表明文献[20]中所给出的解并不是最好解。

为了验证本文的处理约束方法可以提高寻优速度，并可以引入到粒子群以外的其他算法，下面针对典型的和声算法(HS)、差分进化算法(DE)和本文算法进行寻优时间对比实验。实验中，基于焊接梁设计问题，针对约束分别采用常规罚函数法和本文处理方法所用时间见表8。

从表8可以看出，采用本文方法相对于常规罚函数法3种算法寻优时间分别缩短了42.36%、28.72%、13.16%，这表明将本文约束处理方法引入到其他智能优化算法能够明显缩短寻优时间。

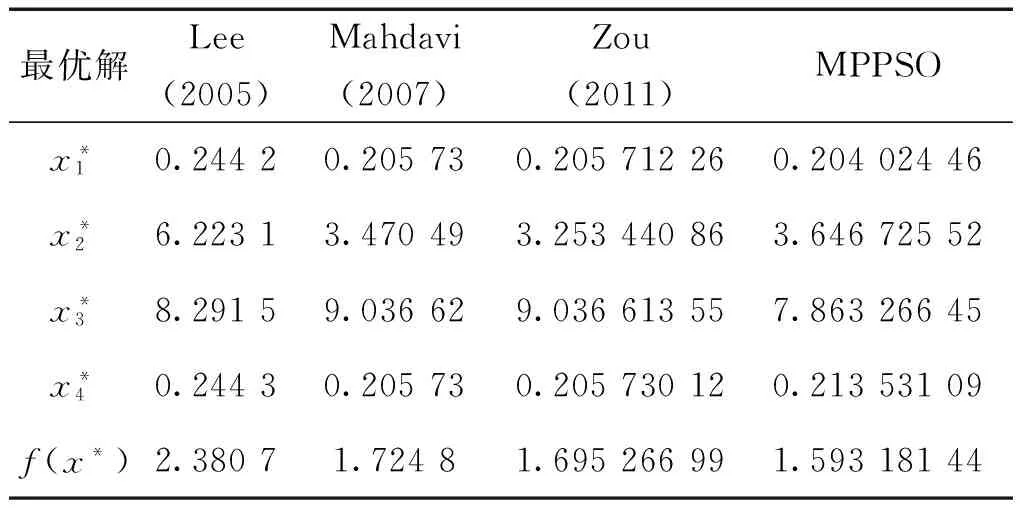
表7 焊接梁设计最优解表

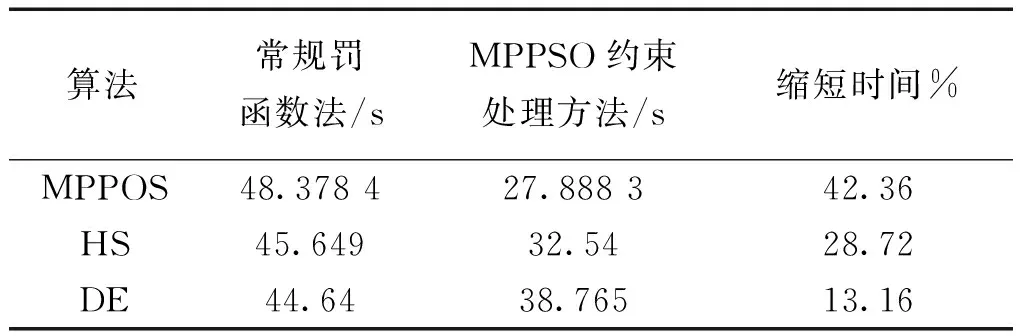
表8 寻优时间对比结果

6 结论

针对粒子群算法收敛精度不高，容易陷入局部最优的缺点，本文提出一种新的多种群随机差分粒子群算法，通过分组和吸引概率的引入，增加了粒子的寻优搜索方向，提高了跳出局部最优的可能性。

1)在速度更新公式中引入具有指导决策功能的变异参数b，对种群的搜索进行有效的指导，有助于解决陷入局部最优问题。

2)在该算法的基础上还给出了一种处理约束的新方法，该方法可以减少计算量，缩短寻优时间。

3)分别对无约束和带约束问题进行了仿真实验，实验结果显示本文算法在处理各类多峰问题时效果明显，优化精度高，收敛速度快。

4)将本文算法应用于焊接梁设计问题，仿真结果也表明其优化效果明显好于现有文献中的已有结果，并且缩短了寻优时间。

[1]NICKABADI A， EBADZADEH M M， SAFABAKHSH R. A novel particle swarm optimization algorithm with adaptive inertia weight[J]. Applied soft computing， 2011， 11(4): 3658-3670.

[2]ANWAR A， MAHMOOD A N. Enhanced estimation of Autoregressive wind power prediction model using constriction factor particle swarm optimization[C]// Industrial Electronics and Applications. [S.l.]， 2014: 1136-1140.

[3]ZHAO X. An enhanced particle swarm optimization algorithm with passive congregation[C]//2010 International Conference on Machine Vision and Human-machine Interface. [S.l.]， 2010: 432-435.

[4]CHIH M， LIN C J， CHERN M S， et al. Particle swarm optimization with time-varying acceleration coefficients for the multidimensional knapsack problem[J]. Applied mathematical modelling， 2014， 38(4): 1338-1350.

[5]ZHAO S Z， SUGANTHAN P N， PAN Q K， et al. Dynamic multi-swarm particle swarm optimizer with harmony search[J]. Expert systems with applications， 2011， 38(4): 3735-3742.

[6]LIANG J J， SUGANTHAN P N. Dynamic multi-swarm particle swarm optimizer[C]//Swarm Intelligence Symposium， 2005. [S.l.]， 2005: 124-129.

[7]KENNEDY J. Bare bones particle swarms[C]//Swarm Intelligence Symposium， 2003. SIS′03. Proceedings of the 2003 IEEE. [S.l.]， 2003: 80-87.

[8]SUN J， FANG W， WU X， et al. Quantum-behaved particle swarm optimization: analysis of individual particle behavior and parameter selection[J]. Evolutionary computation， 2012， 20(3): 349-393.

[9]DANESHYARI M， YEN G G. Constrained multiple-swarm particle swarm optimization within a cultural framework[J]. Systems， man and cybernetics， part a: systems and humans， 2012， 42(2): 475-490.

[10]SAHED O A， KARA K， HADJILI M L. Constrained fuzzy predictive control using particle swarm optimization[J]. Applied computational intelligence & soft computing， 2015， 2015(1): 1-15.

[11]WEN W，HAO Z．Improved particle swarm optimizer based on dynamic topology [J]．Computer engineering and applications，2005，41(34)：82-85.

[12]ZHAN Z H， ZHANG J， LI Y， et al. Adaptive particle swarm optimization[J]. Systems， man， and cybernetics， part B: cybernetics， 2009， 39(6): 1362-1381.

[14]LIANG J J， RUNARSSON T P， MEZURA-MONTES E， et al. Problem definitions and evaluation criteria for the CEC 2006 special session on constrained real-parameter optimization[J]. Journal of applied mechanics， 2006， 41: 8.

[15]VENKATRAMAN S， YEN G G. A generic framework for constrained optimization using genetic algorithms[J]. Evolutionary computation， 2005， 9(4): 424-435.

[16]CABRERA J C F， COELLO C A C. Handling constraints in particle swarm optimization using a small population size[M]//MICAI 2007: Advances in Artificial Intelligence. Springer Berlin Heidelberg， 2007: 41-51.

[17]CAI Z， WANG Y. A multiobjective optimization-based evolutionary algorithm for constrained optimization[J]. Evolutionary computation， 2006， 10(6): 658-675.

[18]WANG Y， CAI Z. Combining multiobjective optimization with differential evolution to solve constrained optimization problems[J]. Evolutionary computation， 2012， 16(1): 117-134.

[19]GAO L， LI S， KONG X， et al. On the iterative convergence of harmony search algorithm and a proposed modification[J]. Applied mathematics and computation， 2014， 247: 1064-1095.

[20]ZOU D， LIU H， GAO L， et al. Directed searching optimization algorithm for constrained optimization problems[J]. Expert systems with applications， 2011， 38(7): 8716-8723.

Multi-population random differential particle swarm optimization and its application

WANG Hao， GAO Liqun， OUYANG Haibin

(School of Information Science and Engineering， Northeastern University， Shenyang 110819， China)

To improve the performance of particle swarm optimization， a new multi-population random particle swarm optimization， based on differential evolution， is proposed in this paper. The proposed algorithm randomly divides the population into several groups and uses the roulette wheel method， based on attraction probability， to determine the possible search direction. When the expected optimization effect is not obvious， this algorithm uses random differential evolution to generate a new solution in the sub-population， aiming to increase the randomness and diversity of the search direction. In addition， a new constraint handling method is proposed to dynamically divide populations. Particle implemented velocity and position updates are proposed to improve search speed. Finally， the proposed algorithm is applied to a numerical optimization problem and a welded beam design problem. Simulation results show that this algorithm has the advantage of high precision and fast convergence when dealing with multi-peak functions. For dealing with a constrained problem， a new method is proposed to handle the constraints， which markedly shortens the search time. The proposed algorithm shows good optimization performance for complex constrained and unconstrained problems.

particle swarm optimization (PSO); multimodal problem; constrained optimization; roulette wheel method；differential evolution；velocity update；position update；search speed； numerical optimization；welded beam design

2015-12-04.

日期：2017-03-18.

国家自然科学基金项目(60674021)；辽宁省教育厅科学研究一般项目(L2014512).

王皓(1981-)，女，讲师，博士; 高立群(1949-)，男，教授，博士生导师.

王皓，E-mail: haohaowang2008@126.com.

10.11990/jheu.201512017

TP301.6

A

1006-7043(2017)04-0652-09

王皓， 高立群， 欧阳海滨.多种群随机差分粒子群优化算法及其应用[J]. 哈尔滨工程大学学报， 2017， 38(4): 652-660.

WANG Hao， GAO Liqun， OUYANG Haibin. Multi-population random differential Particle swarm optimization and its application[J]. Journal of Harbin Engineering University， 2017， 38(4): 652-660.

网络出版地址：http://kns.cnki.net/kcms/detail/23.1390.u.20170318.0715.010.html