High Performance Compressed Sampling for OFDMUWB Systems
2017-05-09LijunGeHuaZhangHuiGuoHongWu
Lijun Ge , Hua Zhang *, Hui Guo , Hong Wu
1 School of Electronics and Information Engineering, Tianjin Polytechnic University, Tianjin 300387, China
2 Tianjin Key Laboratory of Photoelectric Detection Technology and System , Tianjin 30038, China
3 School of Electronics Information and Optical Engineering, Nankai University, Tianjin 300071, China
* The corresponding author, Email: 991926659@qq.com
I. INTRODUCTION
With the growing demands for communication in nowadays, using technologies such as orthogonal frequency division multiplexing(OFDM) and multiple antennas can improve the band efficiency in a certain degree. However, the most direct and effective way to improve the transmission rate is to increase the bandwidth according to the Shannon theory. Ultra-wideband (UWB) communication with frequency band 3-10GHz can achieve 480Mbps as the highest data transmission rate.60GHz communication can get an ultra high speed higher than 5Gbps. OFDM has become the core technology in the field of wide-band wireless communication, for its irreplaceable advantages in high band efficiency communication against multi-path channel. Both the 3-10GHz standard and the 60GHz standard specify OFDM as one of the physical layer schemes, which is applied to wireless personal area network (WPAN), wireless high-definition multimedia interface (HDMI), medical imaging and two-way high-speed data transmission interface.
The implementation of high-speed ana-log-to-digital converters (ADC) is the primary challenge and the technical bottleneck in UWB baseband receivers. According to the Nyquist sampling theorem, the huge bandwidth makes the receiver need ultra high speed ADC to achieve signal sampling, which greatly increases the difficulty of the implementation of the system. A time-interleaved sampling technique satisfied for the Nyquist rate is early proposed, that signal sampling alternates among multiple parallel circuits with low-speed ADC, and the multiplex sampling data join together for output [1][2]. In recent years, researchers try to get rid of the restriction of the Nyquist sampling theorem and engage in the sampling rate reduction methods based on the characteristics of the signal itself.Compressed sensing (CS) is a revolutionary signal sampling and reconstruction theory that a compressible sparse signal can be sampled at a rate far lower than the Nyquist one and recovered with a high probability [3][4]. At present, compressed sensing theory has been applied to many fields of communication and signal processing, such as impulse radio ultra wide band (IR-UWB) systems and image processing [5][6].
However, there are few articles about CS application in OFDM-UWB systems for sampling rate reduction so far. A random demodulation (RD) structure is early proposed for directly compressed sampling of analog signals[7][8]. In this structure, observation sequences, multiplication, integral, low speed sampling and signal recovery are included. On the basis of RD, a parallel segmented compressed sensing (PSCS) structure for OFDM cognitive radio systems is proposed. By changing the rows and the segments of the structure, a balance between the hardware complexity and the compressed sampling rate can be obtained [9].In [10], CS theory is applied to OFDM-UWB systems for the first time that PSCS is adopted to solve the problem of high speed sampling and it takes effect in a certain degree. As the frequency-domain sparse position of OFDM signals is known, the orthogonal matching pursuit (OMP) algorithm is optimized which avoids iterative operation [10]. In the PSCS structure, binary pseudo-random sequences are used as the multiplex observation sequences,getting a good non-correlation effect for precisely signal recovery according to the restricted isometric property (RIP). The modulated wide-band converter (MWC) presented in [11]can capture multiple narrow-band signals with continuous spectrum in a wide band range.However, it is not suitable for OFDM signals carrying useful information via discrete spectrum lines.
In order to solve the problem of highspeed sampling in OFDM-UWB systems,this paper presents an optimized parallel segmented compressed sampling method by constructing orthogonal or quasi-orthogonal observation sequences based on Hadamard matrix.
In this paper, an analysis of the applicability of existing compressed sampling methods to OFDM systems is first given. Then, on the basis of PSCS, a segmented observation model is established, and an optimized parallel segmented compressed sampling (OPSCS)scheme is proposed, constructing the segmented observation matrix with any dimensions by Hadamard matrix. Thus, orthogonal or quasi orthogonal multiplex observation sequences are obtained, and the restricted isometry property is improved. The optimized orthogonal matching pursuit algorithm is also used for the known sparsity. It will be shown that the proposed method has a better performance than the existing compressed sampling schemes and it is even better than the Nyquist rate sampling.
The remaining of the paper contains the following parts: Section 2 briefly reviews the OFDM signal model and the CS theory.Section 3 describes the existing compressed sampling principles and their applicability to OFDM. The proposed scheme for improved segmented observation by orthogonal Hadamard matrix is presented in Section 4. Simulation results are given in Section 5. Finally, in Section 6 the conclusion is presented.
II. OFDM SINGLE AND COMPRESSED SAMPLING MODEL
2.1 OFDM signal model
In OFDM systems, the frequency-domain signal X=[X0, X1, …, XN-1]Tis transmitted by N mutually orthogonal subcarriers. The symbol Xksent over the kth sub-carrier is selected from a PSK or QAM constellation. The time-domain signal through IDFT modulation could be expressed as
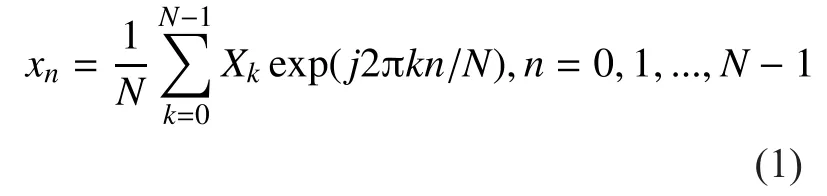
De fine vector x=[x0, x1, … , xN-1]T, (1) could be represented in matrix form as

where vector z=[z0, z1,…, zN-1]Tis the additive white Gaussian noise. After DFT demodulation, the frequency-domain signal is given by

2.2 Compressed sensing principle
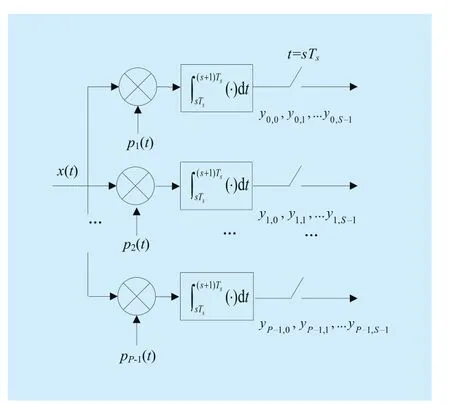
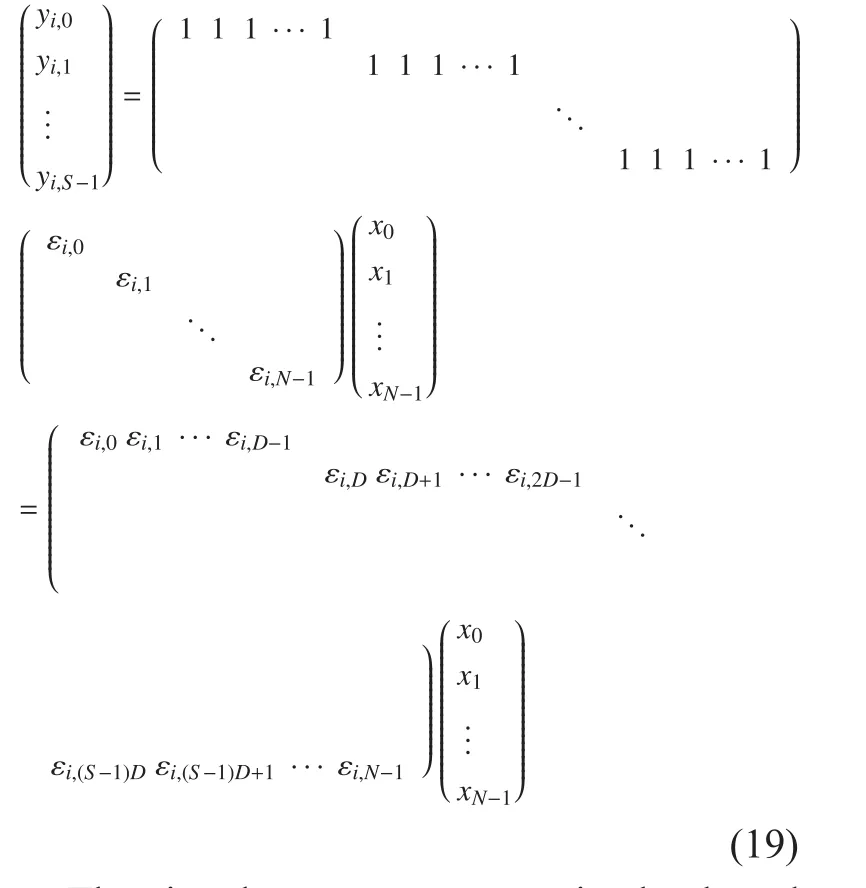
Compressed sensing is a signal compression theory for sparse signals. Define a N×1 signalIt can be mapped by a group of orthogonal basis named Ψ that

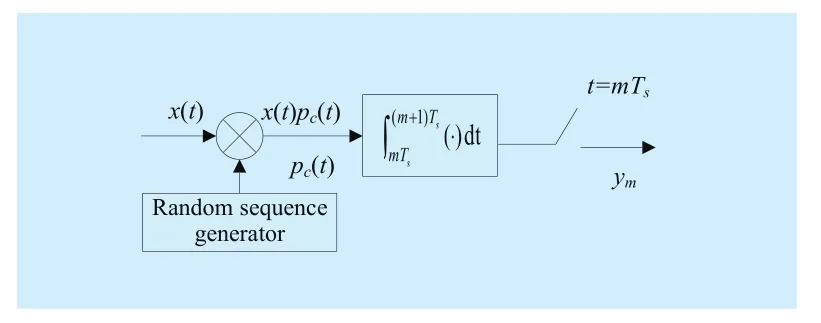
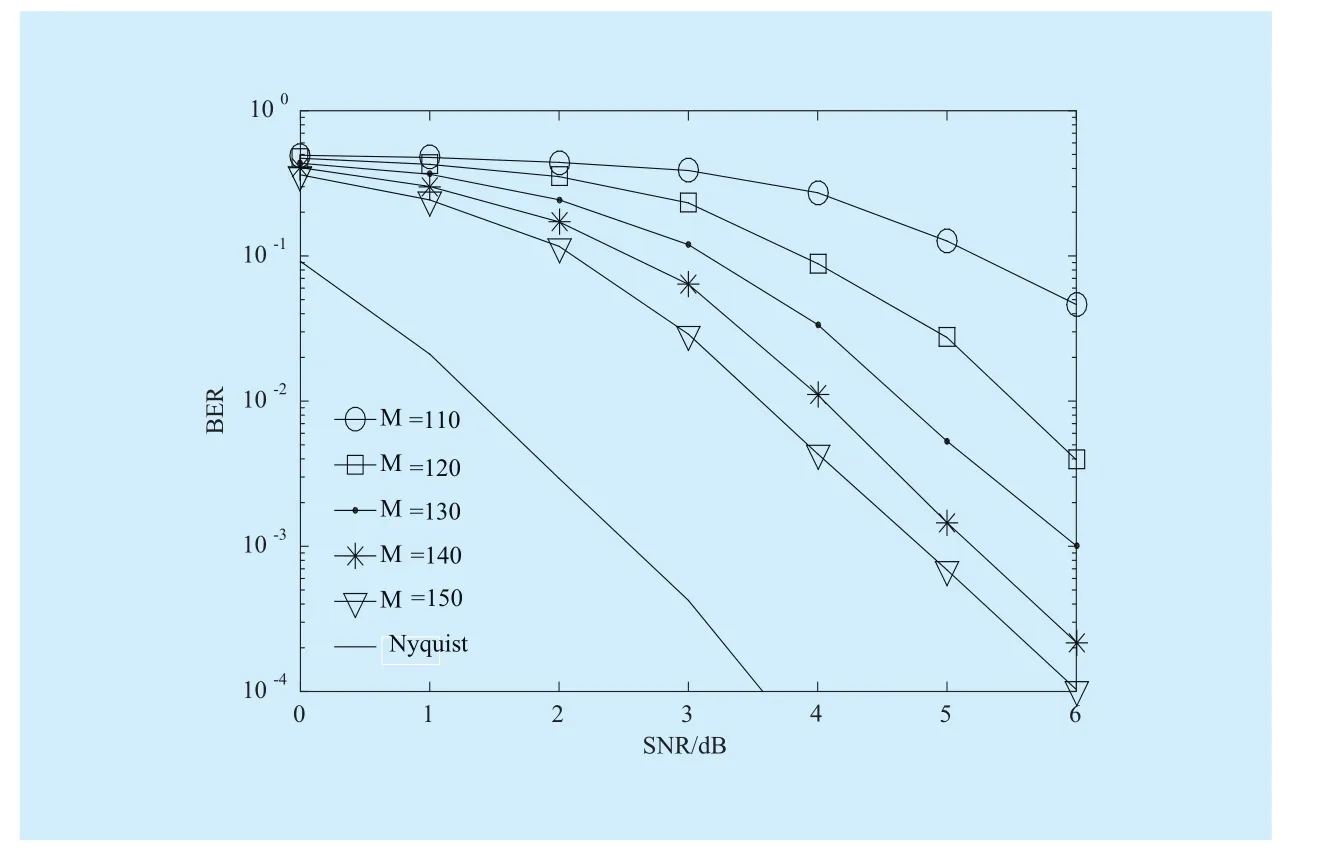
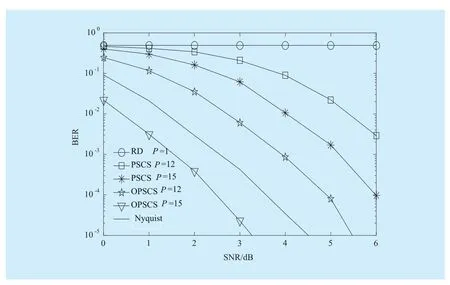
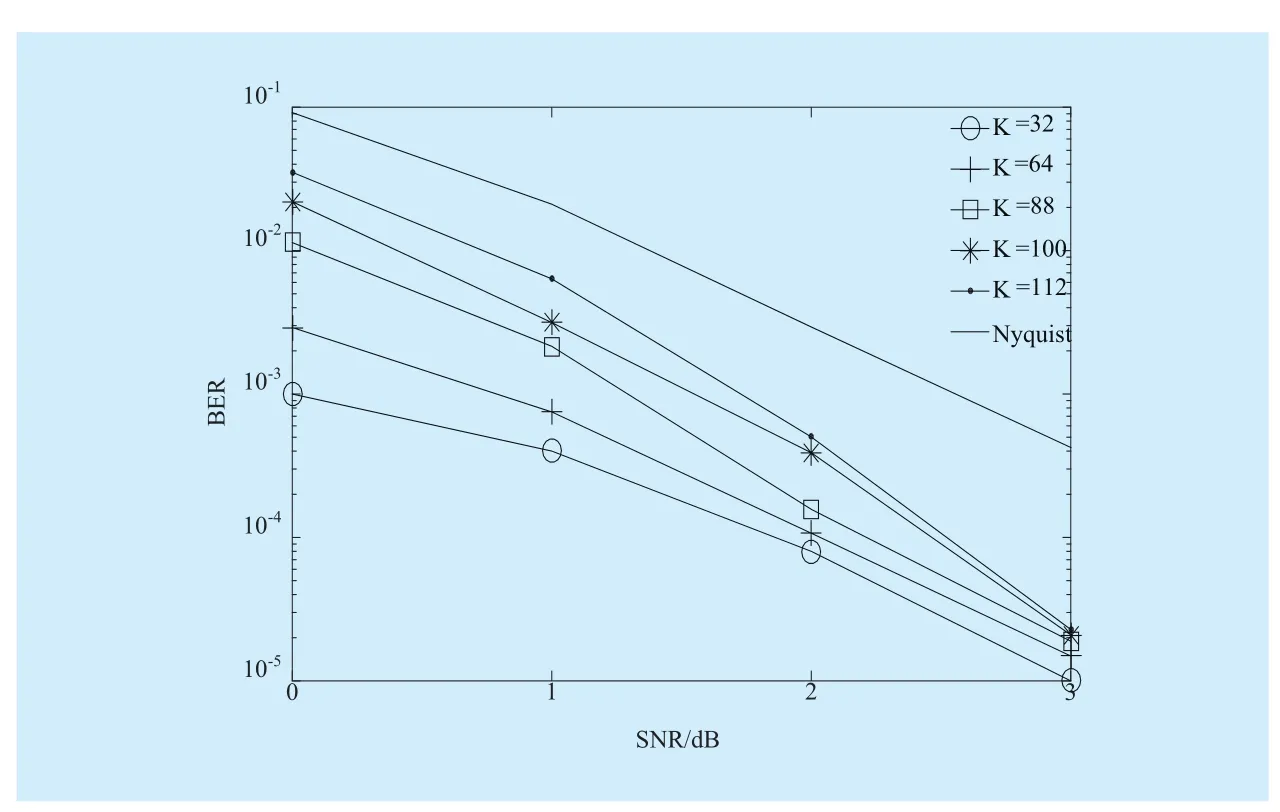
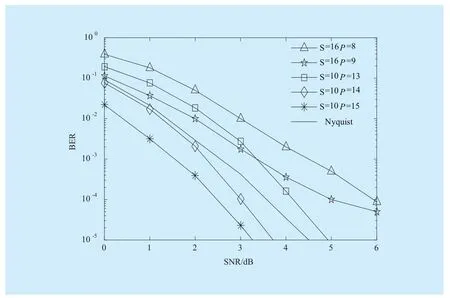
where a is the description of x in Ψ domain. If a has K (K< where c is a small constant [12]. Vector x could be reconstructed by calculating the optimal solution. Classic signal reconstruction algorithms recover x from a small number of observations as follow: where ε is a very small noise value. To get the solution of (9), there are two kinds of method.One is the method based on convex optimization, such as basis pursuit (BP) algorithm.This kind of method is of high reconstruction accuracy, but not easy to implement because of the high computational complexity. The other kind of method is based on greedy iterative, such as matching pursuit (MP) algorithm,orthogonal matching pursuit (OMP) algorithm[13]. The reconstruction via greedy algorithms is not as accurate as that of the convex optimization ones. But the operation is simple that it is easy to be implemented. Comparing (2) and (6), it can be seen that the IFFT transformation basis, by which the frequency domain signal is mapped into time domain, can be viewed as the orthogonal basis of compressed sensing theory in OFDM systems.If the frequency-domain signal X=[X0, X1, …,XN-1]Tonly has K (K< As we can see, (10) meets the basic compressed sensing principle given in (7), so it is feasible in mathematics to apply CS to OFDM compressed sampling. The original frequency domain signal X can be reconstructed from the observation vector y. According to the RIP condition and the relationship (8), the performance of compressed sampling in OFDM systems is determined by the signal sparsity K,the number of sub-carriers N, the number of the observations M, the measurement matrix Φ and the reconstruction algorithm. Figure 1 shows a random demodulation structure which is applicable to analog signal compressed sampling [8]. In the structure, the input signal x(t) is multiplied by the pseudo random sequence p(t),then the random demodulated signal obtained is where Tsis the compressed sampling interval.In order to reconstruct the signal by CS, the analog signal is equivalent to the discrete time signal expressed in matrix form as follow: The integrator next to the multiplier is equivalent to an accumulator in discrete time domain, getting the sum of N/M consecutive entries of the demodulated signal. Therefore,the effect of the sampler can be considered as an M×N matrix H, whose mthrow has D consecutive unit entries starting in column mN/M+1 for each m=0,1,2,…,M-1, where D=N/M and it is assumed to be an integer in this paper.The matrix H with D ones in each row can be expressed as Based on (10), formula (13) can be rewritten as From the previous analysis, it is theoretically feasible for RD to recover K non-zero frequency-domain values from M observations for OFDM systems. Reference [14] also indicates that RD based compressed sampling is suitable for continuous-time signals with discrete line spectrum. As only the spectrum at the frequencies of the sub-carriers needs to be reconstructed in OFDM systems, it can be viewed as a discrete line spectrum. It is feasible to apply RD to OFDM systems in theory, and the compressed sampling rate is M/N multiples of the Nyquist one. However,according to (8), if a high reconstruction accuracy is needed, three factors including the Nyquist-rate data length N, the sparsity K and the observation number M restrict each other.When N is fixed, the larger the sparsity K is,the greater the observation number M needs to be. As we know, OFDM-UWB systems need to transmit a large amount of data, so the sparsity K cannot be very small that it is hard for M to be far less than N. Therefore, it cannot play an obvious role for RD to reduce the sampling rate in OFDM systems. Fig. 1 Structure of random demodulation compressed sampling Based on the RD structure, a parallel segmented compressed sensing (PSCS) structure is proposed in [9]. Figure 2 shows the schematic diagram of this structure. It extends the RD structure to multiple parallel rows. Define the number of rows as P and the number of observations as still M, then the number of observations in each row is S=M/P. In order to explain the PSCS principle more clearly, this paper further gives the equivalent matrix-vector model based on the PSCS structure proposed in [9]. The PSCS structure can be viewed as P parallel RD circuits with S samples produced in each row and P×S samples obtained in the whole structure, so we can establish a row-based equivalent observation model. The ith row of the PSCS structure, i=0,1, … , P-1, based on the RD principle, can be expressed as Fig. 2 Parallel segmented compressed sensing structure The signal recovery process is also based on the row-based observation model (17) (19).As each row has only S observations, it is needed to combine all the M observations in P rows to reconstruct the K non-zero frequency data in OFDM systems. Thus, PSCS can get an obviously higher reconstruction precision than RD under the same sampling rate. Meanwhile, when the number of observations of RD and PSCS are the same, the sampling rate of PSCS is 1/P times of that of RD. Therefore,the PSCS structure is more effective than RD in reducing sampling rate by increasing the system complexity. For sub-sparse OFDM signals, it has a better performance. In order to reconstruct the signal accurately by PSCS, based on (19), the measurement matrix needs to have minimum correlations between rows. Thus, it is essential to analyze the RIP characteristic of the sensing matrix which is composed by P observation sequences in the PSCS structure. For these reasons, this paper further establishes an segment-based equivalent observation model of PSCS, by which the signal is observed and reconstructed. In the PSCS structure, the input signal multiplied by observation sequences can be viewed as S segments divided by the segmented integrator in each row. As the structure has P rows, each segment has P samples that P×S samples are totally included in the structure.Based on the sampling model (19), the observations in the jth segment can be expressed as (20) can be further written as where yj=[y0,j, y1,j, …, yP-1,j]Tis the P×1 compressed sampling sequence in the jth segment,j=0, 1, …, S-1, xj=[xjD, xjD+1, …, xjD+D-1]Tis the input D×1 Nyquist rate sequence in the jth segment, is the nth element of the observation sequence in the ith row, and Φjis the P×D segmented measurement matrix in the jth segment that Formula (21) is the established segmented observation model for PSCS. In order to meet the compressed sensing model, (21) can be further written as where Ψj= ([0],[0], ... [0],Φj,[0],[0] ... [0]) is a P×N matrix, extended from the segmented matrix Φj, with j P×D null matrixes on the left side of Φjand S-1-j P×D null matrixes on the right side. Q is the N×N inverse Fourier transform matrix.is the N×1 input sequence at Nyquist rate. X is the N×1 frequency domain mapping result of x. Based on the segmented observation model(23), the K non-zero values of original OFDM signals are recovered from the total M observations derived from S segments. In order to reconstruct the signal accurately, the samples from different rows should have minimum correlations, and it is equivalent to that the P observations in each segment obtained by(23) have minimum correlations to each other. Therefore, the sensing matrix ΨjQ in (23)needs to meet the RIP condition strictly. In order to make the sensing matrix ΨjQ meet the RIP condition, we can design a suitable matrix Ψjwith minimum correlations between rows, for the Fourier transform matrix Q is a strictly orthogonal basis [15]. As all the elements in Ψjexcept Φjare zero, the correlation of Ψjis equal to that of Φj. Previous researches use pseudo-random sequence as the multiplex observation sequences in PSCS [9-10]. Although the pseudo-random sequence can make the rows of Φjuncorrelated in a certain degree, it is not the ideal state to make them uncorrelated completely, that the measurement matrix does not meet the RIP condition strictly. That leaves a space for improvement. If the rows of Φjare orthogonal to each other, the RIP of the measurement matrix ΨjQ will achieve a great improvement, which is the very point this paper makes a contribution to. To improve the performance of PSCS for OFDM systems, this paper adopts the orthogonal Hadamard matrix to construct the segmented measurement matrix in the segment-based observation model, then the orthogonal or quasi-orthogonal multiplex observation sequences are obtained, which greatly improves the RIP characteristic of the sensing matrix. According to the basic principle of Hadamard matrix [17], it is a n×n matrix, and the elements included are all ±1. It meets the condition of HHT=E, where H is a Hadamard matrix, E is an unit matrix. The dimension of H and E meets the following condition If we take Hadamard matrix as the segmented measurement matrix Φjdirectly, the rows in Φjare orthogonal to each other, and the RIP characteristic is the best. However, because of the limitation of the dimension value n, it cannot achieve any dimensions directly that it cannot be applied to the compressed sampling structure with any rows and segments. In this paper, we propose a scheme to construct the multiplex observation sequences suitable for any rows and segments, based on the basic structure of Hadamard matrix. This compressed sensing scheme has a better RIP than the original PSCS, which is called optimized parallel segmented compressed sampling (OPSCS). Fig. 3 Construction of a 12×16 segmented observation matrix by Hadamard matrix Fig. 4 Construction of a 8×10 segmented observation matrix by Hadamard matrix In the OPSCS structure, the M observations,produced by the compressed sampling from P rows and S segments, are less than the N Nyquist samples which means PS (A) When D meets the condition given by(24), we construct a D×D Hadamard matrix at first, then select any P rows to generate an strictly orthogonal observation matrix. For example, we can select 12 rows from a 16×16 Hadamard matrix to generate a 12×16 orthogonal matrix, as shown in fig. 3, where ik∈[1,16] and ik∈Z*, k=1,2,...12. (B) When D does not meets (24), then: (i) When D and P are both even, it is easy to prove that a P×D matrix can be divided to multiple n×n matrixes, where n meets (24).Thus, we construct an orthogonal or quasi-orthogonal observation matrix by combining multiple Hadamard matrix with different dimensions. During the construction, we should follow a maximum dimension principle, which means let the dimension of Hadamard matrix be maximum orderly. For example, as shown in fig. 4, we can add 4 parallel 2×2 matrixes on the right side of a 8×8 Hadamard matrix to generate a 8×10 measurement matrix. Thus,8×8 is the maximum dimension we can get in a 8×10 matrix, meeting the Hadamard matrix condition. (ii) When D is odd and D+1 meets (24), we construct a (D+1)×(D+1) Hadamard matrix at first, and then select any D columns and P rows, similar to situation (A), getting a quasi-orthogonal measurement matrix. (iii) When D is odd, P is even and D+1 does not meet (24), we construct a P×(D+1)matrix according to (i) at first, and then select D columns from the matrix, getting a quasi-orthogonal measurement matrix. (iv) When D is even, P is odd and D+1 does not meet (24), we construct a (P+1)×D matrix according to (i) at first, and then select P rows from the matrix, getting a quasi orthogonal measurement matrix. According to (22), the observation sequence in the ith row of OPSCS, expressed as, can be obtained from the S constructed segmented measurement matrix Φj. Using this method, orthogonal or quasi-orthogonal observation sequences can be constructed for OPSCS with any rows and segments. On the other hand, when designing the OPSCS structure, we should consider the feature of Hadamard matrix to furthest maintain the orthogonality of the observation sequences from destroying. In the above description, (3) and (5) give the signal model of the OFDM system based on Nyquist rate sampling. If the additive noise in time domain is z, the noise in frequency domain form after DFT can be expressed as Z=QHz. Here for the OFDM system based on OPSCS, we add the noise item to (23), then the segmented compressed sampling signal can be expressed as where zj=[zjD, zjD+1, …, zjD+D-1]Tis the D×1 additive channel noise in the jth segment of OPSCS. The pattern of data distributed on sub-carriers is fixed in OFDM systems, so the number and the positions of non-zero sub-carriers are known. According to the simplified OMP algorithm [10], we can recover the signal by solving the linear equations without estimating the sparsity and its position, which avoids the iterative operation. Specifically, we can solve the M linear equations, derived from the M observations of S segments described in (25), for OPSCS. Thus, the equations in matrix form are where each matrix form equation contains P algebraic equations. The accuracy of solving the above equations depends on two factors: one is the additive noise item in every equation; the other one is the correlations between the equations,the number of equations M and the number of unknowns K. Further analysis on these two aspects is given as follows: (A) As Ψjis composed of +1 and -1 with the same probability, and the expectation of Gaussian white noise is zero, the values of the elements in vector Ψjz are closer to zero and smaller than that in the original noise vector z. (B) If the coefficients of the equations are little correlated or orthogonal, the equations can be solved precisely on condition that M≥K. But if the coefficients are correlated,M>>K is necessary. Besides, the bigger the M is, the more the noise item Ψjz can be eliminated. According to the analysis in the previous section, we know that both pseudo random sequence and Hadamard matrix are composed of ±1, which means they both have the ability to smooth noise. However, compared with the pseudo random sequence, the orthogonal or quasi-orthogonal observation sequences constructed by Hadamard matrix have less correlation, which brings a more accurate solution of the equations. When the numbers of the total observations M are the same, the anti-noise performance of OPSCS is better than that of PSCS. And it may even be better than that of Nyquist rate sampling due to its anti-noise ability, when M is close to N, where N is the number of Nyquist rate samples. Under the same performance of reconstruction and number of circuit rows, fewer observations are needed to recover the original signal.So, OPSCS can reduce the sampling rate more than PSCS for OFDM-UWB systems. To investigate the performance of compressed sampling, we set up a simulation environment of an OFDM system, which includes 128 sub-carriers, 32 zeros based guard interval,OFDM symbols with the length of 160, QPSK modulation and demodulation, 5/8 convolution coding and Viterbi decoding. Then we compare the performances of the three compressed sampling methods including RD, PSCS and the proposed OPSCS. As the sparsity position is known in OFDM systems, all the three methods adopt the optimized OMP algorithm for signal reconstruction. Fig. 5 shows the BER performance of the RD based compressed sampling system under different observations when the sparsity K is 88, and the numbers of observations are respectively 110, 120, 130, 140 and 150. From the figure we can see that the BER gets lower when the number of observations increases.When the number of observations is 150 and the SNR is 5dB, the BER achieves 10-4. When the number of observations is 120, the BER is only 10-1under the same SNR. Besides, the performance of the RD based system is obviously worse than that of the system based on Nyquist rate sampling. Fig. 6 shows the BER performance of RD,PSCS and OPSCS under the same sampling rate, when K is 88. The numbers of the segments of RD, PSCS and OPSCS are all equal to 10, and the row of RD can be viewed as 1.The rows of PSCS and OPSCS are 12 and 15,so that the dimensions of the corresponding segmented observation matrix of OPSCS are 12×16 and 15×16 respectively. From the previous analysis, we can know that the constructed measurement matrixes based on Hadamard matrix are strictly orthogonal. It can be seen from the figure that the performance of PSCS and OPSCS is obviously better than RD, for the observations in PSCS and OPSCS are far more than that in RD, when the sampling rates are the same. It indicates that RD cannot effectively reduce the sampling rate for OFDM-UWB systems. As for PSCS and OPSCS, the performance gets better with the number of parallel rows and observations increasing. And the performance of OPSCS is much better than that of PSCS under the same number of observations. When the SNR is 5dB, and the numbers of the segments and the rows are 10 and 12 respectively, the BER of OPSCS is 3 orders of magnitude lower than that of PSCS. It indicates that the performance of orthogonal observation sequences is much better than that of pseudo random sequences.Meanwhile, the performance of OPSCS under 120 observations is better than that of PSCS under 150 observations. It means that under the same number of rows, OPSCS can reduce the sampling rate more effectively than PSCS,and under the same compressed sampling rate, the structure of OPSCS is less complex.Furthermore, it is shown an important result that when the numbers of rows and segments are 15 and 10, the BER of OPSCS is even lower than that of the Nyquist system, which indicates that OPSCS cannot only precisely reconstruct the signal but also process a good anti-noise performance. On the condition of 10 segments and 15 rows, fig. 7 shows the BER performance of the OPSCS based system when the sparsity K is 32, 64, 88,100 and 112 respectively. The 15×16 segmented measurement matrix is still strictly orthogonal. The figure indicates that the error performance gets better with the sparsity K decreasing, and it is better than that of the Nyquist system under different sparsities. Fig. 8 shows the BER performance of the OPSCS based system with different segments and rows, when K is equal to 88. When the number of segments is 10, and those of rows are 13, 14 and 15, the corresponding segmented observation matrixes are strictly orthogonal. When the number of segments is 16, and those of rows are 8 and 9, the observation matrixes of sizes 8×10 and 9×10 are not strictly orthogonal. As shown in the figure, when the number of segments is fixed, the BER gets lower with the number of observations increasing. Furthermore, when the SNR is 3dB,the BER of the OPSCS with 10 segments and 14 rows is 1 order of magnitude lower than that of the OPSCS with 16 segments and 9 rows. It means that under the same observations, the performance of the system based on strictly orthogonal observation matrix is better than that of the quasi-orthogonal matrix based system. As for the system based on strictly orthogonal matrix, when the number of observations is close to that of the Nyquist rate samples (≥140), the performance of the compressed sampling based system is better than that of the Nyquist system. In order to solve the problem of high-speed sampling in OFDM-UWB systems, this paper presents an optimized parallel segmented compressed sampling method by constructing orthogonal or quasi-orthogonal observation sequences based on Hadamard matrix. According to the segmented observation model established by this paper, segmented measurement matrix with any dimensions is constructed by the orthogonal Hadamard matrix.The simplified OMP algorithm is also used because of the known sparsity. The simulation indicates that OPSCS can reduce the sampling rate in OFDM-UWB systems effectively, and the performance is obviously higher than RD and PSCS. When the number of observations is close to that of Nyquist samples, the performance of OPSCS is even better than that of Nyquist sampling. This work is supported by the National Natural Science Foundation of China (No. 61302062),the National Natural Science Foundation of China (No. 61571244), and the Natural Science Foundation of Tianjin for Young Scientist(No. 13JCQNJC00900). [1] ANDERSON C, VENKATESH S, IBRAHIM J,et al. Analysis and implementation of a time-interleaved ADC array for a software-defined UWB receiver[J]. IEEE Transactions on Vehicular Technology, vol. 58, no. 8, pp. 4046-4063, 2013. [2] ZOU Yuexian, ZHANG Shangliang, LIM Y,et al.Time-interleaved analog-to-digital-converter compensation using multichannel filters[J]. IEEE Transactions on Circuits and Systems, vol. 60,no.4, pp.1123-1131, 2011. Fig. 5 BER performance of RD under different observations when K=88 Fig. 6 BER performance of RD, PSCS and OPSCS under the same sampling rate when K=88 and S=10 Fig. 7 BER performance of OPSCS under different sparsity when S=10 and P=15 Fig. 8 BER performance of OPSCS under different segments and rows when K=88 [3] CANDES E, ROMBERG J, TAO T. Robust uncertainty principles: Exact signal reconstruction from highly incomplete frequency information[J]. IEEE Transactions on Information Theory,vol.52, no.2, pp.489-509, 2006. [4] DONOHO L. Compressed sensing[J]. IEEE Transactions on Information Theory, vol.52,no.4, pp.1289-1306, 2006. [5] ZHOU Qin, ZOU Zhuo, TENHUNEN H,et al.Architectural analysis of compressed sensing based IR-UWB receiver for communication and ranging[C], 2014 IEEE International Conference on Ultra-WideBand (ICUWB 2014). Pairs, France:IEEE Press, pp.222-227, 2014. [6] CHEN Ningyu, WU ShaoHua, LI YunHe,et al.Compressed sensing enabled narrowband interference mitigation for IR-UWB systems[C],2013 International Conference on Wireless Communications and Signal Processing (WCSP 2013). Hangzhou, China: IEEE Press, 2013. [7] LASKA J, KIROLOS S, DUARTE M,et al. Theory and implementation of an analog-to-information converter using random demodulation[C],2007 IEEE International Symposium on Circuits and Systems (ISCAS 2007). New Orleans, LA,United states: IEEE Press, pp 1959-1962, 2007. [8] TROPP J, LASKA J, DUARTE M,et al. Beyond Nyquist: efficient sampling of sparse bandlimited signals[J]. IEEE Transactions on Information Theory, vol. 56, no. 1, pp. 520-544, 2010. [9] YU ZhuizhuaN, HOYOS S, SADLER B. Mixed signal parallel compressed sensing and reception for cognitive radio[C]// 2008 IEEE International Conference on Acoustics, Speech and Signal Processing-Proceedings (ICASSP). Las Vegas, NV, United states: IEEE Press, pp. 3861-3864, 2008. [10] HOSSEINI H, SYED-YUSOF S, FISAL N,et al.Compressed wavelet packet-based spectrum sensing with adaptive thresholding for cognitive radio[J]. Canadian Journal of Electrical and Computer Engineering, vol. 38, no. 1, pp. 31-36,2015. [11] AGRAWAL T, LAKKUNDI V, GRIFFIN A,et al. Compressed sensing for OFDM UWB systems[C], 2011 IEEE Radio and Wireless Symposium (RWS 2011). Phoenix, AZ, United states:IEEE Press, pp. 190-193, 2011. [12] MISHALI M, ELDAR Y. From theory to practice sub-Nyquist sampling of sparse wideband analog signals[J]. IEEE Journal on Selected Topics in Signal Processing,vol. 4, no. 2, pp. 375-391,2010. [13] CANDES E, TAO T. Near-optimal signal recovery from random projections: universal encoding strategies[J]. IEEE Transactions on Information Theory, vol. 52, no. 12, pp. 5406-5425, 2006. [14] LIVSHITZ E, TEMLYAKOV V. Sparse approximation and recovery by greedy algorithms[J]. IEEE Transactions on Information Theory, vol. 60, no.7, pp. 3938-4000, 2014. [15] BARANIUK R. Compressive sensing[J]. IEEE Journals and Magazines on Signal Processing Magazine, vol. 24, no. 4, pp. 118-121, 2007. [16] MICHAEL A, MIKE E, JOHN S. Reconciling compressive sampling systems for spectrally sparse continuous-time signals[J]. IEEE Transactions on Signal Processing, vol. 60, no. 1, pp.155-171, 2012. [17] MONTOLIO P, RIFA J. Construction of Hadamard mathbbZ2mathbbZ4Q8-codes for each allowable value of the rank and dimension of the kernel[J]. IEEE Transactions on Information theory, vol. 61, no. 4, pp. 1948-1958, 2015.
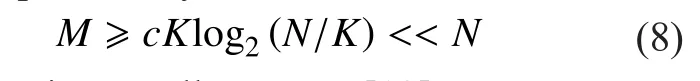
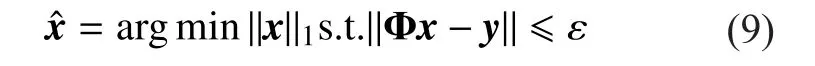
2.3 OFDM compressed sampling model

III. EXISTING COMPRESSED SAMPLING PRINCIPLE AND APPLICABILITY ANALYSIS
3.1 Random demodulation
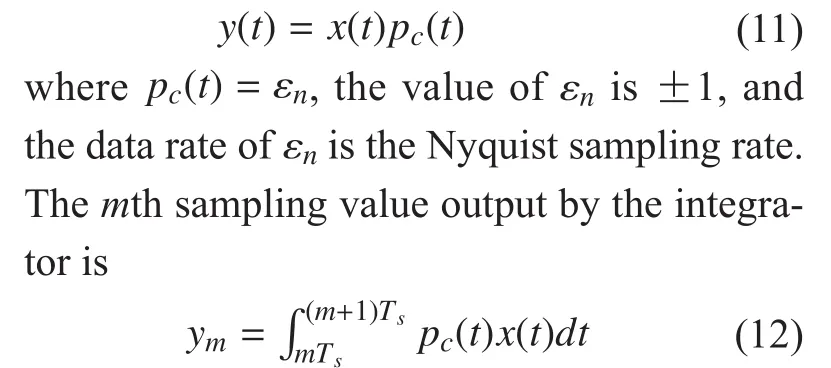

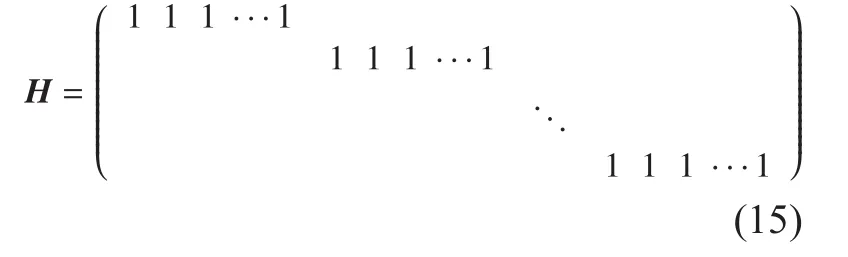
3.2 Parallel segmented compressed sensing
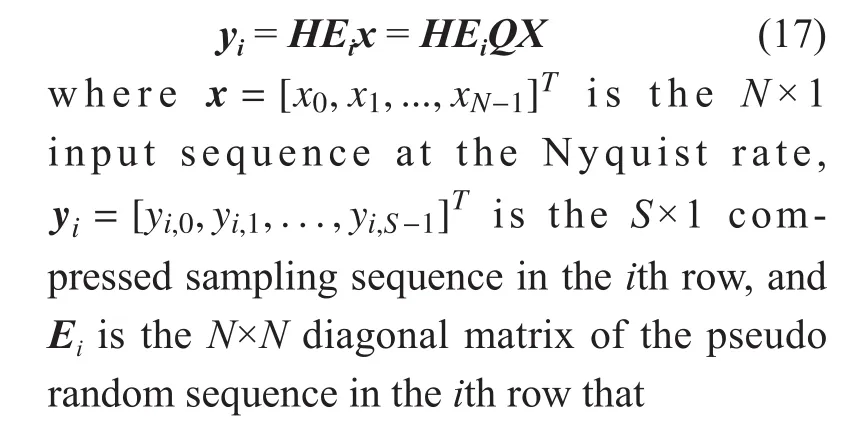

IV. OPTIMIZED PARALLEL SEGMENTED COMPRESSED SAMPLING
4.1 Segmented observation model
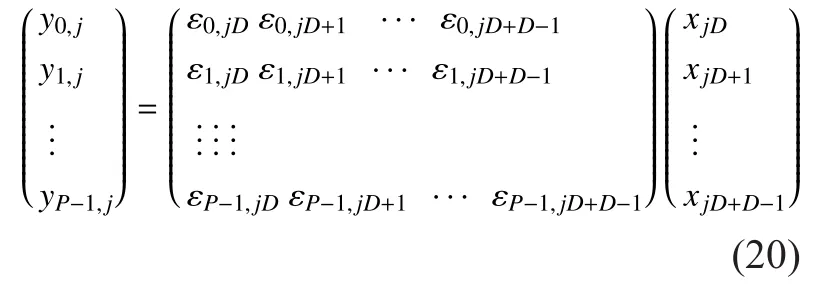

4.2 RIP analysis
4.3 Multiplex observation sequences construction based on Hadamard matrix
4.4 Signal recovery and performance analysis
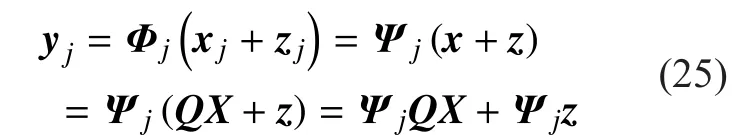
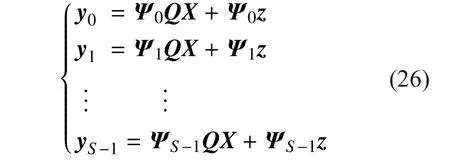
V. SIMULATION ANALYSIS
VI. CONCLUSIONS
ACKNOWLEDGEMENT
杂志排行
China Communications的其它文章
- A Novel Low Density Parity Check Coded Differential Amplitude and Pulse Position Modulation Free-Space Optical System for Turbulent Channel
- Direction of Arrivals Estimation for Correlated Broadband Radio Signals by MVDR Algorithm Using Wavelet
- Signal Path Reckoning Localization Method in Multipath Environment
- Adaptive Application Offloading Decision and Transmission Scheduling for Mobile Cloud Computing
- Degree-Based Probabilistic Caching in Content-Centric Networking
- Efficient XML Query and Update Processing Using A Novel Prime-Based Middle Fraction Labeling Scheme
