基于归一化拟合的电池剩余放电预测问题研究

陈 辉 吴 杰

(安徽商贸职业技术学院， 安徽 芜湖 241002)



基于归一化拟合的电池剩余放电预测问题研究

陈 辉 吴 杰

(安徽商贸职业技术学院， 安徽 芜湖 241002)

通过归一化曲线拟合，得到了不随放电电流变化的内在规律，并构造出放电曲线初等函数表示。任意电流放电数学模型预测的理论数值与实验数据平均相对误差可控制在0.66%。根据不同衰减状态下放电曲线的分析，得出其线性相关的变化规律，预测出不同衰减状态下的放电曲线。此项研究已应用于2016年全国大学生数学建模竞赛C题。

归一化；放电时间；MRE；衰减状态；数据拟合；线性回归

蓄电池电化学反应复杂，由于各种材料、结构、制造工艺及使用环境不同，不同厂家生产的蓄电池也存在较大的特性差异，甚至同一厂家生产的蓄电池，其单体特性也会有一定的离散性。迄今为止，尚没有一种简单有效的电池性能检测方法，电池性能的检测仍是一个复杂的电化学测量难题[1]。电池荷电状态SOC(state of charge) 估计是蓄电池性能检测的一项重要内容，主要检测方法有放电实验法、开路电压法、负载电压法、内阻法、线性模型法、神经网络法和卡尔曼滤波法等[2]。谢德明等人基于改进电化学热力学、动力学和等效电路模型的方法，研究了电池充放电曲线的基本变化特征[3-5]。裴锋等人通过对电流变流放电实验数据与特性的研究，构建了电池组放电效率模型[6-8]。他们根据恒定电流强度的放电过程，描述了电压随放电时间单调下降的变化规律。

2016年全国大学生数学建模竞赛C题，给出了某铅酸电池在出厂时不同电流强度放电测试的完整放电曲线采样数据，以及在不同衰减状态下以同一电流强度从充满电开始放电的记录数据[9]。本次研究通过对上述不同电流强度放电测试的分析，使用归一化曲线拟合，对可以从整体上表示各放电曲线的初等函数作出定义；同时，根据不同衰减状态下的放电曲线分析，得出其线性相关的变化规律，从而通过线性回归预测出不同衰减状态下的放电曲线。通过这些研究，较好地解答了2016年全国大学生数学建模竞赛C题。

1 数据处理与初步分析

在蓄电池放电开始的数十秒内，有一个端电压陡降但又很快回升并进入正常放电的过程，此过程称为电压陡降复升。有剩余荷电的蓄电池在放电瞬间仍然会出现这种现象[10-11]。为了得到电池持续的放电特性，应对不同电流强度放电测试采样数据进行处理。图1所示为电池放电曲线。

图1(a)中，将电池放电初期经过电压陡降后可以恢复的最高点记为(t0,V0)，记电源电压降到保护电压Um的时刻为tmax，即最大放电时间。对应每个放电电流，都可以计算对应放电过程的tmax、t0和V0。得到各放电曲线的典型参数见表1。去除放电初期出现的电压陡降数据之后，即可得到图1(b)所示各种放电曲线。

记各放电数据所在的曲线为V=f(t)，则V0=f(t0)，Um=f(tmax)。为考察不同电流放电曲线之间的变化规律和内在联系，首先使用表1中的数据将放电曲线V=f(t)归一化，即将每条曲线的自变量和函数值都转化到区间[0, 1]。

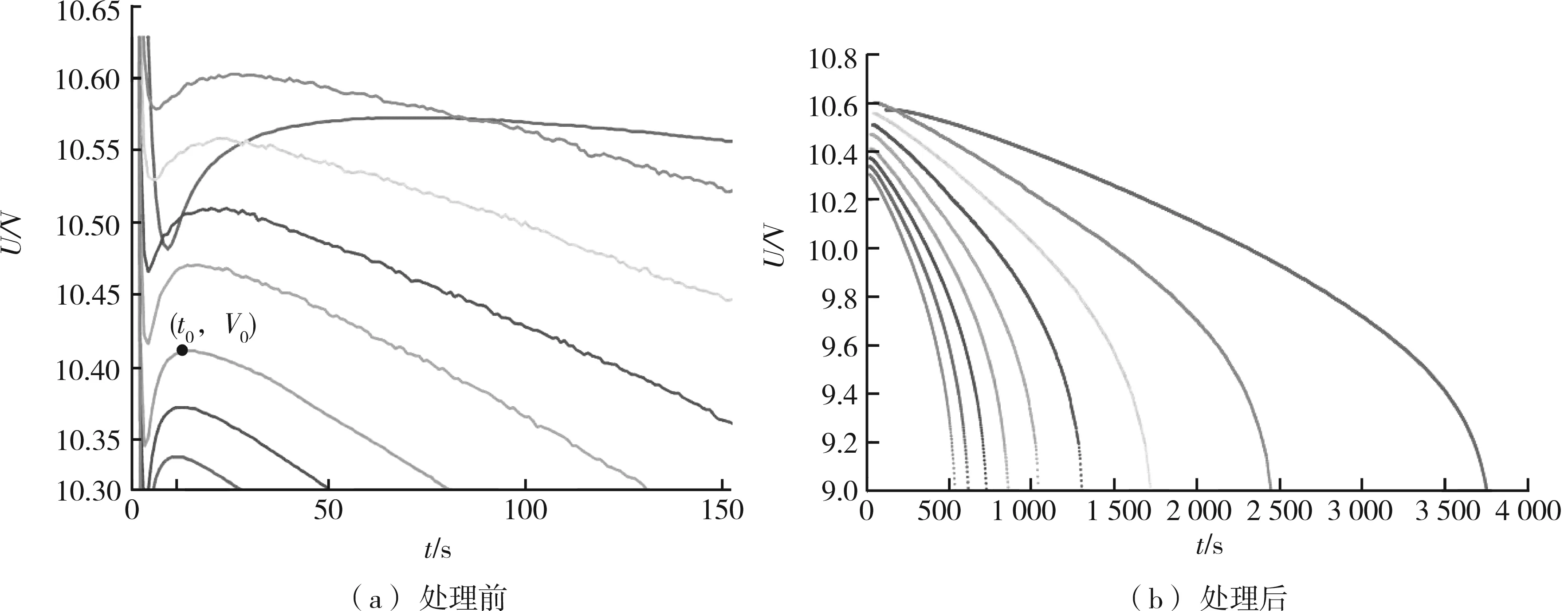
图1 电池放电曲线

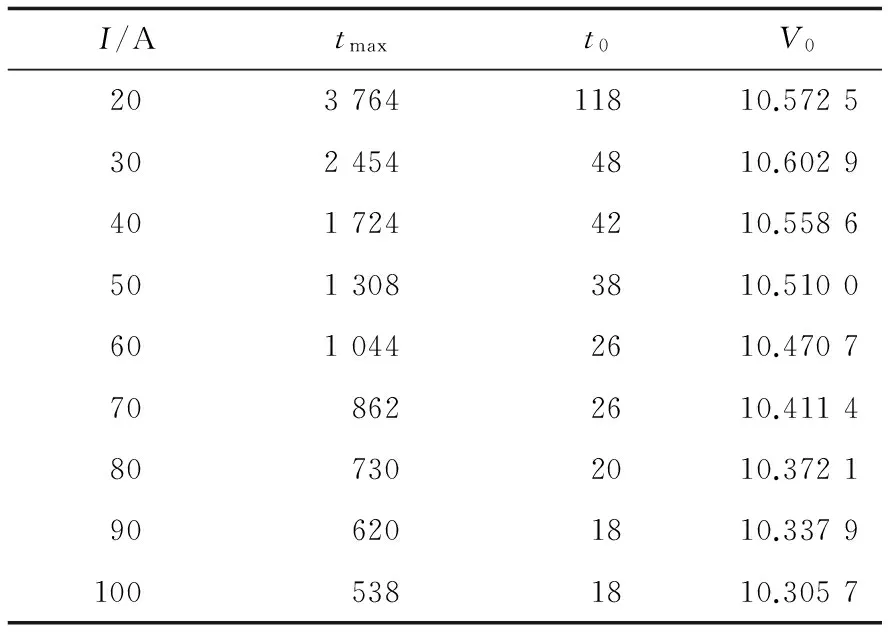
I/Atmaxt0V020376411810.57253024544810.60294017244210.55865013083810.51006010442610.4707708622610.4114807302010.3721906201810.33791005381810.3057

自变量t和函数V变换为：

(1)

图2 归一化后的放电曲线拟合效果

经过归一化处理后，各电流的放电曲线几乎都集中在同一条曲线上，那么这条曲线反映了一种不随着放电电流变化、与电池自身性能紧密相关的内在规律。将这条曲线对应的函数关系称为归一函数，可以将其函数表达式通过拟合解析出来。观察到曲线经过原点和(1,1)点并且下凹，使用如下经验函数进行拟合：

y=a(1-x)b+1

(2)

通过拟合:

a=-1.014 333 919 028 390

b=0.505 460 276 993 855

拟合优度指标效果良好:SSE， 0.662 7；R-square，0.998 2；Adjusted R-square，0.998 2；RMSE， 0.0102。

2 放电曲线的初等函数表示

将式(1)带入式(2)，使用归一函数重构放电曲线，得到“归一函数模型”：

船舶污染物接收处置能力的硬件能力，主要表现为获得充足的人力、物力、信息等资源支持的可能性。船舶污染物接收处置的任何活动都离不开一定的资源供给和支撑。基于全面资源论，按照所需配置资源的自然属性，船舶污染物接收处置能力的硬件能力可以分为对人力资源、物力资源、信息资源三个方面的配置能力。其中的物力资源配置能力主要指设备设施的配置能力，按照船舶污染物接收处置流程可以将其分为船舶存储设备设施、接收设备设施、转运设备设施和处置设备设施的配置能力。还可按照船舶污染物种类进行划分，如船舶垃圾接收设施、生活污水转运设施、含油污水处置设施等。

(3)

其中，V0、t0和tmax取表1中的对应值。重构的放电曲线与初始实验数据之间的拟合效果良好，如图3 所示。

(4)

计算平均相对误差，即MRE(见表2)，MRE的平均值为0.66%。利用放电曲线预测电池剩余容量放电时间时，其精度取决于放电曲线在低电压段的质量，计算的MRE误差情况见图4。

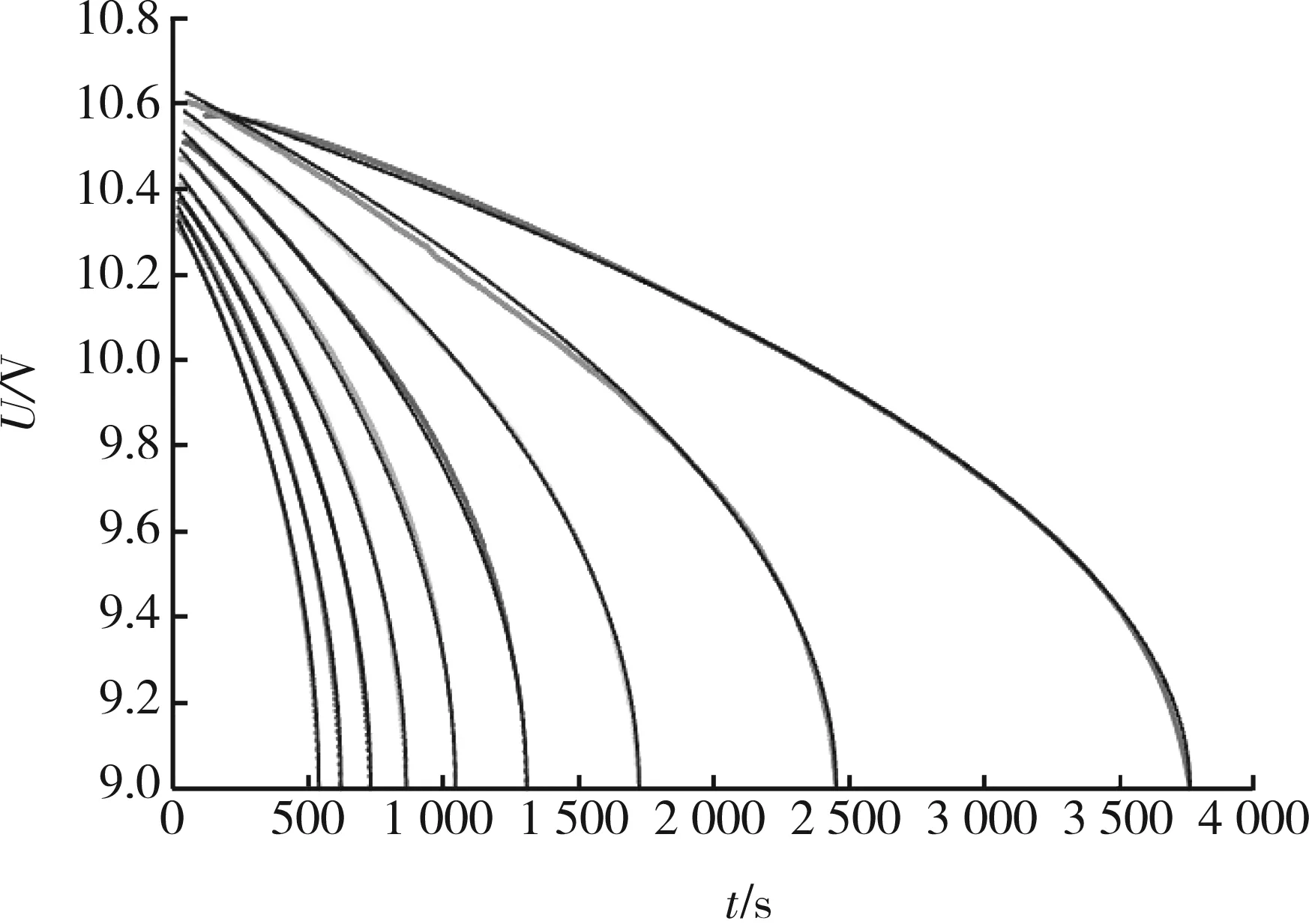
图3 重构出的放电曲线拟合效果

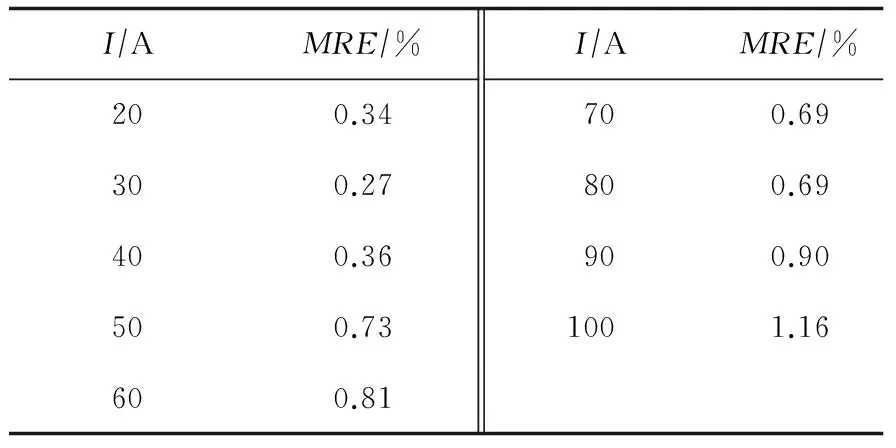
表2 放电曲线的MRE %

与现有文献结果相比，上述计算具有一定优势[3-8]。首先，保持了比较高的精度，涵盖全部放电电流的平均相对误差为0.006 6，最大不超过0.011 6，最小为0.002 7。其次，式(3)中的各个参数都具有明确的实际含义，并且对所有的放电电流构建了统一、整体的初等的函数表示，相对于使用遗传算法、模拟退火和神经网络等内部拟合机制不明的复杂算法[12-14]，为电池性能监测系统装置的设计带来了极大的便利。

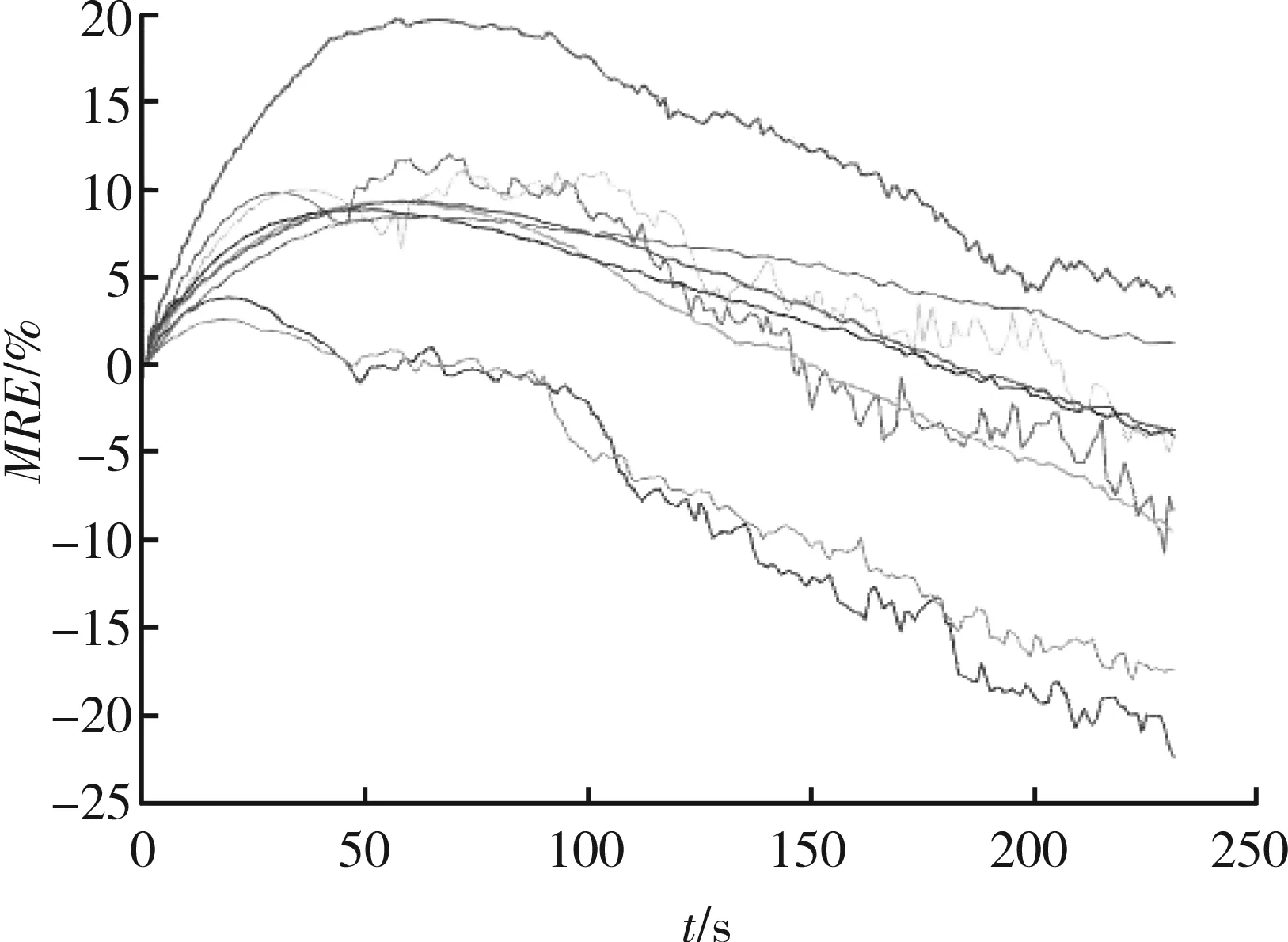
图4 计算的MRE误差分布

3 任意电流放电数学模型

如果可以找到V0、t0和tmax随电流I变化的规律，则模型(3)可以转化为只与电流I和时间t有关的函数，而不依赖于表1中的数值。观察9条放电曲线的V0、t0和tmax随电流I变化的趋势。

拟合随电流变化的V0：

V0(I)=a1·I+b1

(5)

拟合随电流变化的t0：

t0(I)=a2·e-b2·I+c2

(6)

拟合随电流变化的tmax：

tmax(I)=a3·e-b3·I+c3

(7)

式(5)—(7)中的参数取值见表3，拟合效果见图5。

表3 V0、t0和tmax的曲线拟合及优度指标

图5 V0、t0和tmax随I变化的曲线拟合效果

将式(5) — (7)带入式(3)，得到20～100 A范围内任意恒定电流强度放电时的放电曲线数学模型：

(8)

其中，

V0=a1·I+b1

t0=a2·e-b2·I+c2

tmax=a3·e-b3·I+c3

拟合效果如图6所示。根据式(8)，重新计算得到表4所示MRE值，平均MRE为3.91%。

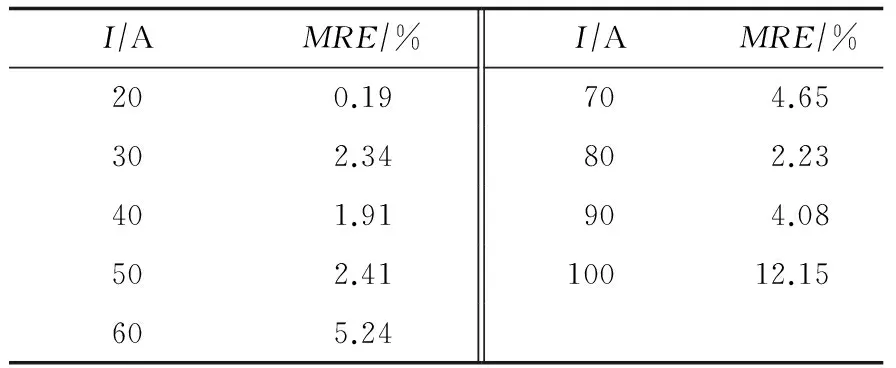
I∕AMRE∕%I∕AMRE∕%200.19704.65302.34802.23401.91904.08502.4110012.15605.24

由于多次拟合造成的误差不断累积，新的模型虽然更通用、灵活和方便，但精度有所下降。由表3可以看出，V0和tmax的拟合已经达到了相当高的精度水平，t0与蓄电池放电时电压陡降复升密切相关，有待进一步研究[10-11]。

4 蓄电池衰减状态的预测

根据同一电池在不同衰减状态下以同一电流强度从充满电开始放电的记录数据，可以预测当前衰减状态的剩余放电时间。根据上述分析，在去除放电开始初期的异常数据(每条曲线的前19项数据)并进行归一化。如图7所示，4条曲线几乎重合。

图7 不同衰减状态下的放电曲线及归一化效果

由此可见，不同状态下的电池归一化放电形态几乎一致，即他们之间存在线性关系，可以建立多元线性回归。将衰退状态3下的放电时间记作因变量Y，新电池放电时间、衰退状态1放电时间和衰退状态2 放电时间看作自变量，依次记作X1，X2，X3，确定多元回归模型：

Y=β0+β1X1+β2X2+β3X4

确定系数R2为0.999 87，统计量F为325 987.87，检验概率P为0，剩余标准差为1.822 5，回归模型成立，并且拟合效果较好(见图8)。可以预测，衰减状态3 的剩余放电时间为最大放电时间801.93，与当前放电时间596.20的差为205.73。

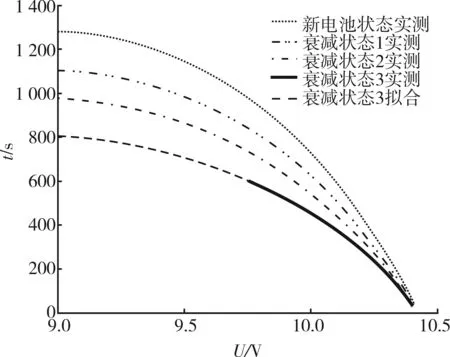
图8 衰减状态3下的放电曲线线性回归

5 结 语

通过对恒电流放电曲线的归一化曲线拟合，找到了不同放电电流下内在的统一的放电规律，在保证较高精度(MRE为0.66%)的同时，构建了全部电流放电的整体初等函数模型，为电池性能监测系统装置设计提供了有效的理论依据。

针对蓄电池在不同衰减状态下以同一电流强度放电，构建了多元线性回归模型。通过现有蓄电池衰减状态下的现有放电记录数据，拟合并预测了当前衰减状态下的放电情况，取得了较好的结果。

[1] 仲伟峰,王海英,李革臣.基于DSP的蓄电池智能在线监测系统设计[J].东北林业大学学报,2008,36(8):58-59.

[2] 林成涛,王军平,陈全世.电动汽车SOC估计方法原理与应用[J].电池,2004,34(5):376-378.

[3] 谢德明,吴瑞峰,蒋盛芳.电池充放电曲线基本变化特征的分析[J].河南师范大学学报(自然科学版),2013(2):107-111.

[4] 王军平,陈全世.电动车用镍氢电池模块的充放电模型研究[J].西安交通大学学报,2006,40(1):50-52.

[5] 黄秋安,栾婷.锂离子电池界面电容充放电深度的计算与分析[J].华中科技大学学报(自然科学版),2016,44(7):25-29.

[6] 裴锋,黄向东.电动汽车动力电池变流放电特性与荷电状态实时估计[J].中国电机工程学报,2005,25(9):164-168.

[7] 黄万友,程勇.纯电动汽车磷酸铁锂电池组放电效率模型[J].华中科技大学学报(自然科学版),2012,40(5):129-132.

[8] 赵建华,欧阳光耀,徐建飞,等.现代潜艇铅酸蓄电池放电模型研究[J].武汉理工大学学报(交通科学与工程版),2006,30(4):675-677.

[9] 全国大学生数学建模竞赛2016年赛题[EBOL].http:∥www.mcm.edu.cnhtml_cnnode6d026d84bd785435f92

e3079b4a87a2b.html.(2016-09-20).

[10] 吴寿松.谈谈铅蓄电池放电时的电压陡降[J].蓄电池,2004,41(3):113-114.

[11] 陈立宝.对铅酸蓄电池放电时电压陡降复升的认识[J].蓄电池,2005,42(3):128-129.

[12] 黄亮,胡恒生,胡恩勇.基于灰色理论的航空铅酸蓄电池剩余容量预测[J].电源技术,2012,36(7):1005-1006.

[13] 刘和平,许巧巧.自适应卡尔曼滤波法磷酸铁锂动力电池剩余容量估计[J].重庆大学学报(自然科学版),2014,37(1):68-74.

[14] 林瑞霖.最小二乘支持向量机在蓄电池剩余容量建模中的应用研究[J].海军工程大学学报,2010,22(5):52-55.

Study on Residual Discharge Prediction of Battery Based on Normalized Curve Fitting

CHENHuiWUJie

(Anhui Business College of Vocational Technology, Wuhu Anhui 241002, China)

Based on the normalized curve fitting, the intrinsic law of the battery discharge function under different steady current is found, and the exact elementary function representation of each discharge curve is constructed. The MRE of the theoretical and experimental data can be controlled at 0.66%. The analysis of discharge curves at different attenuation states shows the linear variation of the discharge curves, and the linear regression is used to predict the discharge curves at different attenuation states. The results of the research succeed in solving the problem C of Contemporary Undergraduate Mathematical Contest in Modeling in 2016.

normalization; battery discharge time; MRE; attenuation; data fitting; linear regression

2016-11-01

安徽省质量工程项目“高等数学大规模在线开放课程示范项目”( 2015MOOC154)；安徽省质量工程项目“经济应用数学大规模在线开放课程示范项目”( 2014MOOC084)

陈辉(1983 — )，男，讲师，研究方向为代数学。

O441

A

1673-1980(2017)02-0115-05