Power Allocation for Wireless Powered MIMO Transmissions with Non-Linear RF Energy Conversion Models

Liqin Shi, Liqiang Zhao, Kai Liang

State Key Laboratory of Integrated Service Networks, Xidian University, Xi’an 710071, China

* The corresponding author, email: lqzhao@mail.xidian.edu.cn

I. INTRODUCTION

Energy harvesting has emerged as a promising technology to prolong the lifetime and improve the scalability of some energy constrained networks. Among different technologies of energy harvesting, radio frequency(RF) wireless energy transfer (WET) by capturing ambient RF radiation and converting it into a direct current (DC), is comparatively controllable compared to traditional natural energy sources, such as wind and solar. Thus,RF WET has attracted a lot of interest from both academia and industry [1].

For the system of RF WET, there are many resource allocation algorithms. Energy-efficient simultaneous wireless information and power transfer was studied in [2], where power allocation, user scheduling, and subcarrier allocation were considered. Different energy management policies were studied in [3–5].[3] studied the optimal polices for transmissions with energy harvesting nodes in fading wireless channels. [4] studied the power allocation for an energy harvesting transmitter with hybrid energy sources. [5] studied the optimal green energy utilization in multiple-input multiple-output (MIMO) systems with hybrid energy supplies.

However, all the aforementioned works were designed based on the linear energy conversion model, where the conversion efficiency was a constant. All those resource allocation algorithms were implemented at the transmitter with the assumption that the RFDC circuit was modeled as a linear energy conversion model.

In practice, the conversion efficiency of the RF-DC circuit varies with the input power level. In general, for low input power, the conversion efficiency increases with increasing input power, but there are diminishing trends and limitations on the maximum possible harvested energy [6]. The conventional linear conversion model cannot catch the non-linear property of the RF-DC circuit. For some input powers of the RF-DC circuit, the conversion efficiency with the linear model is much higher than that with the practical RF-DC circuit.

Thus, the system performance was overestimated in [2-5] due to the conventional linear energy conversion model. In practice,the practical RF-DC circuit is used to convert the RF energy at the receiver, which leads to a mismatch for the resource allocation in [2-5]. Because with the linear energy conversion model, the resource allocation is optimal but with the practical RF-DC circuit, this resource allocation may not be optimal.

In this paper, we propose a power allocation algorithm with the consideration of the non-linear energy conversion models. The contributions of our work are summarized as follows:

· We study three existing energy conversion models and compare these three models with the experimental data from the practical RF-DC circuits. The results show that the linear model is inaccurate for the practical RF-DC circuits.

· We propose a power allocation algorithm

with the above non-linear models to maximize the energy efficiency of the system under multiple constraints, i.e., the transmission power, the received power and the minimum harvested energy at the receiver.Numerical results show that our proposed algorithm with the non-linear energy conversion models can achieve much better performance than the algorithm with the conventional linear model.

II. SYSTEM MODEL

We consider a wireless powered time division duplex (TDD) MIMO communication system including a base station (BS) withantennas and a user equipment (UE) withantennas.Assume that the BS and UE operate over the same frequency band and both of them are perfectly synchronized. Each slot can be divided into two phases, downlink (DL) WET and uplink (UL) wireless information transmission(WIT). The duration of a slot lastsseconds.Therefore, DL WET and UL WIT account forandsecondsrespectively. We ignore the feedback process and assume that the channel state information (CSI)are perfectly known at the BS through the fed back from the UE. For convenience, we normalizein the rest of this paper without loss of generality.

2.1 DL WET phase

At this phase, the BS transmits energy to the UE by wireless energy beamforming.

1) Energy Harvesting

where is thefirst column of the unit matrix, andis the maximum eigenvalue of.

Fig.1 Comparison between the harvested powers for two non-linear energy conversion models and the measurement data from two different practical RF-DC circuits with different dynamic ranges from [10] and [11]

Fig.2 Comparison of the conversion efficiency for two non-linear energy conversion models and the experimental data for [10]

2) Energy Harvesting Models

[9] proposed a heuristic model for the conversion efficiency as a function of the input power, andis given by:

According to most existing RF-DC circuits,the input power level ranges from 0 to 4 mW.

[6] proposed a practical parametric non-linear model based on the sigmoidal function andcan be obtained by:

We compare the two non-linear energy conversion models with the experimental results from [10] and [11] as shown in Fig. 1 and Fig.2. Fig. 1 and Fig. 2 show that the two nonlinear energy conversion models basically match experimental results from [10] and [11]. The heuristic model is more accurate than the sigmoidal model with a small input power, while the sigmoidal model is more suitable with a large input power. Besides, both Fig. 1 and Fig. 2 illustrate that the linear model is not ac-curate in modelling non-linear RF-DC circuits.

2.2 UL WIT Phase

In this phase, the UE will use the harvested energy to transmit information. The received signal at the BS can be obtained by

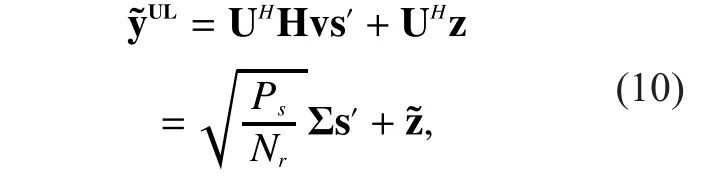
The UL data rate (in bits/s/Hz) is given by

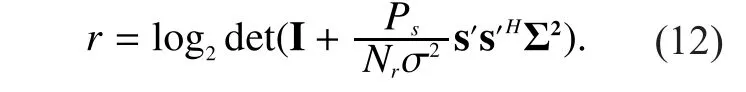
III. PROBLEM FORMULATION AND SLOUTION

3.1 Problem formulation

In this paper, the design objective is the maximization of the energy efficiency of the system and the optimization problem can be mathematically formulated as:

Since the objective function in (14) is a ratio of two functions, (14) is non-convex. Letas the maximum energy efficiency andcan be obtained by:

According to [14], the objective function can be transformed as:

3.2 Solution

In this subsection, we use the Dinkelbach method to solve (14). As shown in Algorithm 1, the algorithm will converge to the optimal energy efficiencyand we have to solve the inner problem (17) in each iteration.

w h e r e holds. Substituting[12, 13] intowe can obtain

1) Linear Model

2) Sigmoidal Model

?

Table I The heuristic model of different rf-dc circuits

Thus, the problem (17) is convex forwith the sigmoidal model.

3) Heuristic Model

The parameters of the heuristic model for different RF-DC circuits are given in Table I [9], where. Substituting the parameters in Table I into [9], we can find thatalways holds forand C3 can be transformed asfor most RF-DC circuits, wherecan be obtained by using bisection method.

Thus, for most RF-DC circuits, the problem(17) is convex forwith the heuristic model.With (17) convex, one-dimensional search methods such as the golden section search method can be used to solve (17).

IV. NUMERICAL RESULTS

In this section, we show the performance of our proposed algorithm. The basic parameters throughout the simulations unless otherwise specified, are as follows. The power of the channel noise isW. The maximum transmit poweris 3W. We consider a block flat fading channeldenotes the large scale fading andrepresents the Rayleigh fading coefficients.For simplicity, we let the propagation constantthe path loss exponentthe propagation distancemeters and shadow fading

We compare the proposed algorithms with three energy conversion models (the linear model, the sigmoidal model and the heuristic model respectively) with maximum transmission power transferin energy efficiency. For convenience, we denote the proposed algorithms with three models as Linear model,Sigmoidal model and Heuristic model respectively and maximum transmission power transfer as MTPT. At the BS, transmission power is allocated based on Linear model, Sigmoidal model, Heuristic model and MTPT, respectively. At the UE, we use the practical RF-DC circuit to convert RF energy. For analytical tractability, the practical RF-DC circuit is modeled as the sigmoidal model or the heuristic model according to the precision of the model.

Firstly, Fig. 3 demonstrates the convergence of the proposed algorithm for different sets of transmitting and receiving antennas and different transmission time. It is observed that the energy efficiency, as discussed before,always converges to the optimal value within a limited number of iterations.

Fig.3 Energy efficiency versus number of iterations with different sets of transmitting and receiving antennas and different transmission time

Fig.4 shows the energy efficiency of the system versus the transmission time of WET under the RF-DC circuit with parameters obtained from [11] under different scenarios,whereandThe conversion efficiencyin the linear model isfixed as 0.4 to satisfy C3 andis fixed as 0.0015J. The heuristic model cannot model this RFDC circuit because the input power of the circuit exceeds the scope of the input power for the heuristic model. As shown in Fig. 4, the energy efficiency of Sigmoidal model is the highest compared with the energy efficiency of Linear model and MTPT.The gap between Sigmoidal model and Linear model in energy efficiency is caused by the mismatch between the linear model and the practical non-linear RF-DC circuit. In general,with the increasing of, the energy efficiency increases at first, then decreases. The numerical results show the same changed trend. Sinceis not small enough, there is a downward trend with Sigmoidal model and MTPT.

Fig.5 shows the energy efficiency of the system versus the transmission time of WET under the RF-DC circuit with parameters obtained from [10] under different scenarios, where

Fig.4 Energy efficiency versus transmission time of WET under the RF-DC circuit with parameters obtained from [11] under different scenarios. (a) The BS and UE are equipped with 3 and 2 antennas, respectively. (b) It is considered as

Fig.5 Energy efficiency versus transmission time of WET under the RF-DC circuit with parameters obtained from [10] under different scenarios. (a) The BS and UE are equipped with 3 and 2 antennas, respectively. (b) It is considered as

V. CONCLUSIONS

In this paper, we study a system of wireless energy and information transmission which applies TDD MIMO protocol. We make an analysis for the practical RF-DC circuits and list three energy conversion models, the linear model,the sigmoidal model and the heuristic model respectively. A comparison is made between the three models and the experimental data to show that the linear model is inaccurate for the practical RF-DC circuits. Considering the practical non-linear RF-DC circuits, the power allocation algorithm is proposed to maximize the energy efficiency of the system. Numerical results show that the proposed algorithm with the non-linear energy conversion models can achieve better performance compared with the algorithm with the conventional linear model.

ACKNOWLEDGEMENTS

This work was supported in part by National Natural Science Foundation of China(61372070), Natural Science Basic Research Plan in Shaanxi Province of China(2015JM6324), Ningbo Natural Science Foundation (2015A610117), Hong Kong, Macao and Taiwan Science & Technology Cooperation Program of China (2015DFT10160), and the 111 Project (B08038).

[1] ULUKUS S, YENER A, SIMEONE O,et al. Energy harvesting wireless communications: A review of recent advances[J].IEEE J. Sel. Area Commun.,vol. 33, pp.360 - 381, 2015.

[2] NG D W K, LO E S, and SCHOBER R. Wireless Information and Power Transfer: Energy Efficiency Optimization in OFDMA Systems[J].IEEE Trans.Wireless Commun., vol. 12, pp. 6352-6370, Dec.2013.

[3] OZEL O, TUTUNCUOGLU O, YANG Jing,et al.Transmission with energy harvesting nodes in fading wireless channels: Optimal policies[J].J. Sel. Area Commun., vol. 29, pp. 1732 -1743,2011.

[4] AHMED I, IKHLEF A, NG D W Ket al,Power allocation for an energy harvesting transmitter with hybrid energy sources[J].IEEE Trans. Wireless Commun., vol.12, pp.6255-6267, 2013.

[5] HU Congshi, GONG Jie, WANG Xiaolei,et al.Optimal green energy utilization in MIMO systems with hybrid energy supplies[J].IEEE Trans.Veh. Technol., vol. 29, pp. 1732 - 1743,2011.

[6] BOSHKOVSKA E, NG D W K, ZLATANOV N,et al.Practical non-linear energy harvesting model and resource allocation for SWIPT systems[J].IEEE Commun. Lett., to be published, DOI:10.1109 /LCOMM. 2015.2478460.

[7] ZHANG Rui and HO C K, MIMO broadcasting for simultaneous wireless information and power transfer[J].IEEE Trans. Wireless Commun.,vol.12, pp. 1989-2001, 2013.

[8] XU Jie and ZHANG Rui. Energy beamforming with one-bit feedback[J].IEEE Trans. Signal Process., vol.62, pp.5370-5381, 2014.

[9] CHEN Yunfei, SABNIS-THOMAS K and ABD-ALHAMEED R, New Formula for Conversion Efficiency of RF EH and its Wireless Applications[J].IEEE Transactions on Vehicular Technology., 2016.

[10] LE T, MAYARAM K, FIEZ T, Efficient far- field radio frequency energy harvesting for passively powered sensor networks[J].IEEE J. Solid-State Circuits., vol. 43, pp. 1287-1302, 2008.

[11] GUO Jiapin and ZHU Xinen, An Improved Analytical Model for RF-DC Conversion Efficiency in Microwave Rectifiers[J].IEEE MTT-S Int. Microw.Symp. Dig., June 2012, pp. 1-3.

[12] JIANG Yi, LI Jian, and HAGER W W, Joint transceiver design for MIMO communications using geometric mean decomposition[J].IEEE Trans.Signal Process, vol.53, pp.3791-3803, 2005.

[13] SHEN Zukang, HEATH R W, ANDREWS J G,et al.Comparison of space-time water- filling and spatial water-filling for MIMO fading channels[C].IEEE Globecom 04, vol.1, pp. 431-435, 2004.

[14] NG D, LO E, and SCHOBER R. Energy-efficient resource allocation in multi-cell OFDMA systems with limited backhaul capacity[J].IEEE Trans. Wireless Commun., vol. 11, no. 10, pp.3618-3631, Oct. 2012.

[15] BIGLIERI E, PROAKIS J, SHAMAI (SHITZ) S, Fading channels: information-theoretic and communications aspects[J].IEEE Trans. Inf. Theory,vol. 44, pp. 2619-2692, 1998.