Underdetermined Blind Source Separation of Adjacent Satellite Interference Based on Sparseness
2017-05-08ChengjieLiLidongZhuZhongqiangLuo
Chengjie Li, Lidong Zhu, Zhongqiang Luo
1 National Key Laboratory of Science and Technology on Communications, University of Electronic Science and Technology of China,Chengdu, China
2 School of Automation & Information Engineering, Sichuan University of Science and Engineering, Zigong, China
I. INTRODUCTION
Recently years, adjacent satellite interference is more and more serious with the increase quantity of satellites. The causes of the adjacent satellite interference are about as the following [1]:
● The adjacent satellite antenna direction is deflected, which leads to the adjacent satellite receiving the target signal which should be sent to the satellite carrier.
● The adjacent satellite antenna sidelobe is too high to meet the criterion of net test, so part of the power is taken to the adjacent satellite.
● The adjacent satellite antenna is too small. Although through the net test standard but need high transmitting power. So, the signal of the antenna sidelobe is sent to the adjacent satellite.
● The adjacent satellite transmitting power is too high.
Because of the hopping frequency signal has high security and good anti-jamming capability, so the hopping frequency signal is widely used in military field and modern satellite communication system. So a novelFHsignal Blind source separation (BSS) of adjacent satellite interference is discussed in this paper.
BSS focuses on extracting and recover source signals from mixed signals with little knowledge on compositions or mixing history[2,3], so BSS is well applicable in many fields,such as image recognition, speech enhance-ment, biomedical signal processing, wireless communications etc. [4-6]. The framework of blind source separation is shown in Fig.1. To this day, many blind source separation algorithms are proposed, such as INFOMAX algorithm, JADE algorithm and FastICA algorithm [7-9], but they require more sensors than sources if little prior information given.Furthermore, many BSS algorithms assume that source signals are statistically independent or mixture is full of rank, but it is not the case in real world [10]. So underdetermined blind source separation (UBSS) needs to be proposed. In this article, we propose an underdetermined blind source separation method of adjacent satellite interference, that is, Density Clustering algorithm (DC-algorithm), which is based on Euclidean distance and sampling points density in time-frequency domain. The problem is described as follows: givenNsampling points in time-frequency domain, each object is assigned to one ofKclusters (the number of the mixed signal isK).
Data clustering algorithm has been widely used in blind source signal separation, whose characteristic is the data within one cluster are very similar while the data between clusters are dissimilar [11-13]. Such asK-means cluster algorithm, which is a familiar cluster algorithm with advantages:1)simplicity,2)efficient [14,15], as well as disadvantages:1)prior knowledge on cluster number,2)strong dependency of performance on original centroid,3)frequent partial optimization [16].
In this paper, blind source separation problem is formulated as clustering problem,which is motivated by the fact that the mixed signal is sparse and the energy difference is as large as possible to satisfy cluster centers that are surrounded by neighbors with local lower density. Basically, to evaluate the similarity among data objects in time-frequency domain,the Euclidean distance measurement is used.The Euclidean distances among every object is described as below [17]:

The rest of this paper is organized as follows. In Section II, we introduce the preparatory work of Density Clustering algorithm(DC-algorithm). In Section III, we introduce the DC-algorithm. In Section IV, we discuss the algorithm performance and analyze the algorithm by the considering the noise and robustness analysis. In Section V, we introduce and discuss the experimental results. Finally,the conclusion is drawn in Section VI.
In this paper, the authors propose frequency hopping signal underdetermined blind source signal separation of Adjacent Satellite Interference.
II. PREPARATORY WORK
In this section, we introduce the related preparatory work of DC-algorithm.
2.1 Sparse BSS
Sparseness means that the possibility is very low that two or more source signals at the same time-frequency points. In the frequency hopping signal time-frequency domain, sparse representation leads to good separation because most of the energy in the defined basis coefficient according to any time-frequency point belongs to a single source. So, sparseness is essential for the Density Clustering algorithm (DC-algorithm), which is easy to satisfy for frequency hopping signal in time-frequency domain. According to the sparseness assumption, the BSS can be described as follows [18,19],

In formula (2),Tdenotestransfer matrix, which denotes the degree of correlation between independent sourcesAand their basis sparse coefficients matrixC. So, the goal in this article can be described as follows: we are in search of the mixed matrixAand transfer matrixT. In order to be more effective effect,the basis coefficients matrixCmust be sparse as far as possible.

Fig. 1 Framework of BSS model
Several existing measures are introduced which can assess the sparseness of signals,such asis used in [20], normalized ratio of theandare used in [21] for signal assessment of the sparseness.In this article, the sparseness measure is considered in time-frequency domain of frequency hopping signal and the method of sparseness measure isD-measure, which is introduced in[22], Fig.2 illustrates the sparseness degrees of three different matrices gauged by theD-measure. It can be seen that the sparseness of matrix is along with the value ofD-measure.
2.2 Frequency hopping signal model
As a kind of non-stationary signal, FH signal changes along with time as below [23]:

here

Fig. 2 Description of various degrees of sparseness. The D-measure values corresponding to the three matrices (from left to right) are 0.1, 0.5, and 0.8, respectively
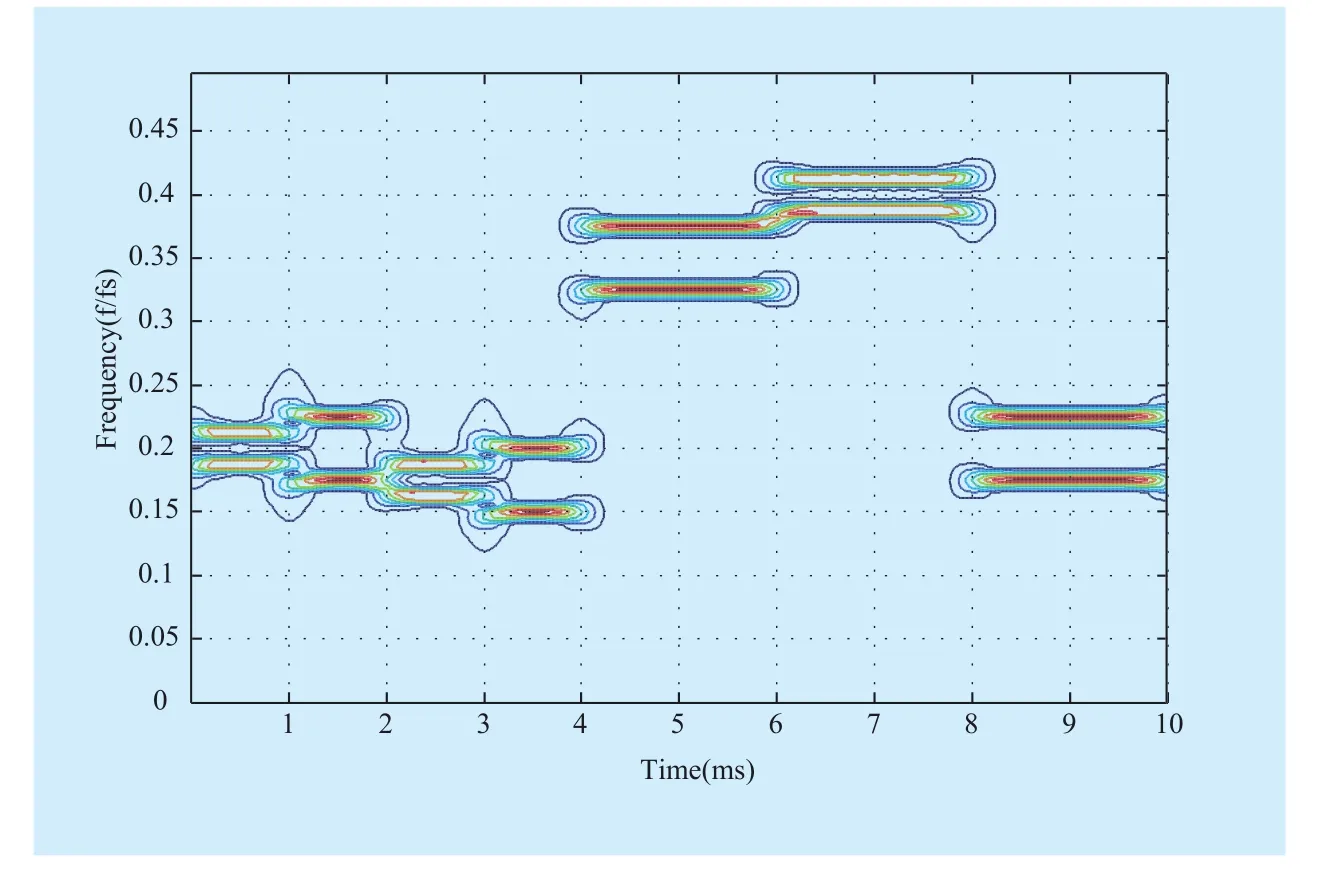
Fig. 3 Image of frequency hopping signal in time-frequency domain
In Fig.3, the image of frequency hopping signal in time-frequency domain is shown.From Fig. 3, we can find finite sine waveforms are unique decided by the following three parameters: the location ofkth hop in time domain; location ofkth hop in frequency domain; length of time- frequency domain [24].
In this article, we focus on separation of initial frequency hopping signals without any other prior knowledge.
III. DENSITY CLUSTERING ALGORITHM(DC-ALGORITHM)
3.1 Construct cost function pair
The novel algorithm in this paper has two assumptions: (1) the source mixed signals are sparse in time-frequency domain. (2) The mixed signal energy difference is as large as possible. The assumption (1) makes the blind source separation question be clustering question, the assumption (2) makes separation as effective as possible. The three-dimensional figure of the received mixed signals in time-frequency domain is described in Fig. 4,
In the above Fig. 4, the vertical axis isthe design formula ofis described in formula (4) [25],
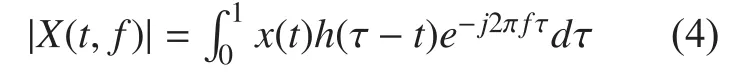
where
For each sampling pointsi, we compute two quantities [26],

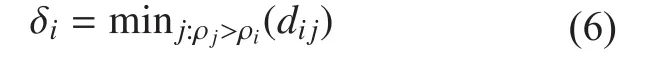
From the above analyses, we can construct the Cost Function Pair.Based on the Cost Function Pair, we can classify the sampling points.
3.2 Construct decision coordinate system
In the following paragraph, the Decision Coordinate System will be constructed, which is the core of the algorithm, which is illustrated by the embedded sample points in Fig. 5 [27].
In the Decision Coordinate System, the horizontal axis isthe vertical axis isIt is seen that although the data number 2 and 22 are very near, they are not the cluster center due to the small value of. Meanwhile, we can see from Fig.5 that data 2 and 22 belong to different centers, i.e., 5 and 19 respectively.Hence, only the data will be treated as cluster center, which are both large values ofand large values of, such as data number 5 and 19 in Fig. 6. The points 14, 15, and 23 are of relatively highand a low, so, they can’t be treated as cluster centers. The result that sampling data points are ranked in order of decreasing density is described in Fig. 6.
After finding the cluster centers, every sample point will be assigned to the nearest cluster center according to Euclidean distance.

Fig. 4 Distribution of frequency hopping signal in time-frequency domain

Fig. 5 Sampling point distribution. ranked in order of decreasing density

Fig. 6 Decision coordinate system. sampling data points are ranked in order of decreasing density
3.3 Estimation of the number of sources
In the following paragraph, the number of source signals will be estimated. The number of source signals can be automatically confirmed according to the Decision Coordinate System in 3.2, however, the results may sensitive toIn the proposed model, the Cost Function Pairis used as sparseness criterion for individual sampling points of the source signals. So, the sparseness will be forced to require as a necessary parameter. Of course, this will increase the complexity of the algorithm.
In order to reduce the complexity of the calculation, we propose an alternative automatic approach for estimation of the number by using the Cost Function Pairin Decision Coordinate System.
In general, we estimate the number of the original signals with the coordinate of every sampling points in Decision Coordinate System. In Fig.5, 5 and 19 are the centers of respective source signal. Then, the number of the original signals in Fig.5 is two.
IV. ALGORITHM PERFORMANCE ANALYSIS
4.1 Considering the noise
To get efficient separation, we construct the cost function, which is described in the following formula [28],


Table I Robustness of algorithm in this article compared with other algorithms
where,
To seek the optimal solution, the noise cannot be neglected and the orthogonal matching pursuit (OMP) algorithm can be used [29].During seeking the optimal solution, in the dictionary update stage, there is an important advantage, that is, the dictionary does not get the existing noise. According to the characteristics of seeking the optimal solution process,the performance of the estimated signal will be high-efficiency according to this dictionary. In the next iteration, the dictionary atoms will be refined. During seeking the optimal solution, a clean signal is achieved by repeating this progressive denoising loop.
4.2 Robustness of DC-algorithm
In the following subsequent sections, the robustness of the algorithm in this article is discussed.
Robustness is used here to mean that the number of Pearson’s correlation coefficient above 0.95 is acceptable under the same test times. The Pearson’s correlation coefficient is defined as:

So, robustness should not be considered here with sensitivity analysis, which is a study of the influence of hybrid matrix changes on performance.
Table 1 reveals that algorithm in this article offers a generally highest percentage of trials (reaching acceptable solutions) and the highest robustness averaged over all the test algorithms. The algorithm in this article reaches the acceptable solutions against other algorithms. Note that the Number of Pearson’s correlation coefficient is above 0.95 of Classical Searching and Averaging Method, FastICA Algorithm, JADE Algorithm are 176, 172,184, respectively. For the mean robustness of all the test algorithms, DC-algorithm offers the highest robustness of 196, followed by JADE Algorithm, classical searching and averaging method and FastICA Algorithm.
According to the theorem of ‘no free lunch’[30], one algorithm cannot offer better performance than all the others on every aspect or on every kind of problem. This is also observed in our experimental results. DC-algorithm outperforms classical searching and averaging method, FastICA Algorithm, JADE Algorithm on separation robustness. However, on average time, FastICA Algorithm offers better performance than DC-algorithm.
V. SIMULATION RESULTS
In this paragraph, some simulations are operated to verify the proposed method in this article. In the following simulations, without loss of generality, we separate the mixed signals in time-frequency domain of frequency hopping signal.
Each parameter is defined as follows:
● The transmission bit rate is
● The modulation frequency is
After having gotten the sampling points,we design the Decision Coordinate System according to the Cost Function Pairin Fig.7. From Fig. 7, we can confirm that the sampling points have three cluster centers. That is to say, the number of the source signals is three.
Every sampling point is assigned to the nearest neighbor cluster according to its density when the cluster centers are found. The results of classification are displayed in Fig.8.As we expected, the sampling points are di-Hz;
● The bit numbers arem=8;
● The original signal numbers areMK=3;
● The receiving antenna numbers arevided into three groups.

Fig. 7 Decision coordinate system of the sampling points based on

Fig. 8 The class of the sampling points
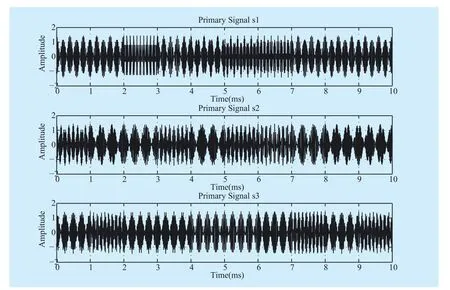
Fig. 9 The sent source signals’ waveforms. three sent source signals are considered
In Fig. 9, the original signal’s waveforms are displayed respectively. In the following experiment, our goal is to separate each signal from the received mixed signals. According to the actual situation, considering to the realistic signal transmission, we adopt two receiving antennas, the signal after Gaussian channel,the received mixed signal waveforms are shown in Fig. 10 (Received Composite Signal).

Fig. 11 Separated waveform with the proposed density clustering algorithm (dc-algorithm)
5.1 The first comparative experiment of eff ect
We use the method in this article for signal blind source separation, the original signals are recovered efficiently. The separated signal waveforms are displayed in Fig., where three signals are shown. It is quite clear that the separated waveform using DC-algorithm is very similar to original signal waveform.
We compare the two signals between Fig. 9 and Fig. 11 with objective evaluation function respectively. We use Pearson’s correlation coefficient as the objective evaluation function,which is defined in (8).
To illustrate the algorithm performance superiority, we further compare the separation performance with the K-means clustering algorithm [31]. The results of the comparison are shown in Fig. 12. From Fig. 12, we can see the source mixed signals can be separated with DC-algorithm, and have better separation performance thanK-means clustering algorithm.
The algorithm framework of the first comparative experiment of effect is shown in Table 2.

Table II Main detail of the algorithm in this article
5.2 The second comparative experiment of eff ect
From 5.1, we can judge the Density Clustering algorithm (DC-algorithm) has good separation effect. In the following section, to further illustrate DC-algorithm has an outstanding separation performance, we will choose another evaluation function, that is, Error Performance Analysis (PI), as evaluation standard, which is defined as:

We compare the separation performance with classical Based on the Ratio Matrix Clustering Algorithm, the comparison result is shown in Fig. 13. From Fig. 13, we can draw a conclusion, the separation performance of DC-algorithm is better than Ratio Matrix Clustering Algorithm [32].
VI. CONCLUSION
In this paper, we propose frequency hopping signal underdetermined blind source signal separation of Adjacent Satellite Interference.Firstly, we get the original data by computing the Short Time Fourier Transform (STFT) of each observation. Secondly, we construct Cost Function Pairand Decision Coordinate System. In Decision Coordinate System, we can conclude the number of the source signals and every sample point will be assigned to the nearest cluster center according to Euclidean distance. At last, we use some simulation experiments verify our proposed algorithm. The experiment results demonstrate the effectiveness of the proposed method.
ACKNOWLEDGEMENT
This work is fully supported by a grant from the national High Technology Research and development Program of China (863 Program)(No.2012AA01A502), and National Natural Science Foundation of China (No.61179006),and Science and Technology Support Program of Sichuan Province(No.2014GZX0004).

Fig. 12 Blind source separation result, this article method has a better performance than classical FastICA algorithm

Fig. 13 Blind source separation result, this article method has a better performance than classical based on the ratio matrix clustering algorithm
[1] Sun Long Wang, Wei Chen, Ning Hua Zhu, Jian Guo Liu, Wen Ting Wang,Jin Jin Gu, A Novel Optical Frequency-Hopping Scheme for Secure WDM Optical Communications,IEEE Photonics Journal. Frequency-Hop Scheme for WDM Communications, Vol.7, No.3, June 2015.
[2] Atiyeh Alinaghi, Philip JB Jackson, Qingju Liu,and Wenwu Wang, Joint Mixing Vector and Binaural Model Based Stereo Source Separation,IEEE/ACM Trans. on Audio, Speech, and Language Processing, Vol.22, No.9, Sep.2014,pp.1434-1448.
[3] Chengpu Yu, Lihua Xie, and Yeng Chai Soh,Blind Channel and Source Estimation in Networked Systems,IEEE Trans. on Signal Processing, Vol.62, No.17, Sep.1, 2014, pp.4611-4626.
[4] Ondrej Tichy and Vaclav Smidl, Bayesian Blind Separation and Deconvolution of Dynamic Image Sequences Using Sparsity Priors,IEEE Trans.on Medical Imaging, Vol.34, No.1, Jan.2015,pp.258-266.
[5] Zhang Ye, Cao Kang, Wu Kangrui, Yu Tenglong,Zhou Nanrun, Audio-Visual Underdetermined Blind Source Separation Algorithm Based on Gaussian Potential Function,China Communications, Communications System Design, June 2014, pp.71-80.
[6] Leonardo T. Duarte, Joao M.T.Romano, Christian Jutten, Karin Y. Chumbimuni-Torres, and Lauro T. Kubota, Application of Blind Source Separation Methods to Ion-Selective Electrode Arrays in Flow-Injection Analysis,IEEE Sensors Journal,Vol.14, No.7, July 2014,pp.2228-2229.
[7] Aapo Hyvarinen, Gaussian Moments for Noisy Independent Component Analysis,IEEE Signal Processing Letters, Vol.6, No.6, Jun.1999, pp.145-147.
[8] GU Fanglin, ZHANG Hang, ZHU Desheng, Maximum Likelihood Blind Separation of Convolutively Mixed Discrete Sources,China Communications, June 2013, Digital Communications,pp.61-67..
[9] Petr Tichavsky, Zbynek Koldovsky, and Erkki Oja,Performance Analysis of the FastICA Algorithm and CramerCRao Bounds for Linear Independent Component Analysis,IEEE Trans. on Signal Processing, Vol.54, No.4, April 2006, pp.1189-1230.
[10] Belouchrani A, Abed-Meraim K, Cardoso JF,etal., A blind source separation technique using second order statistics,IEEE Transactions on Signal Processing, Vol.45, No.2, 1997, pp.434-444.
[11] W.Barbakh, Y.Wu, C.Fyfe, Review of clustering algorithms, in: Non-Standard Parameter Adaptation for Exploratory Data Analysis,Springer,Berlin/Heidelberg, 2009, pp.27-28.
[12] A.K.Jain, Data clustering: 50 years beyond K-means,Pattern Recognition Letters31 (2010)651-666.
[13] Wenjie Bi, Meili Cai, Mengqi Liu, and Guo Li, A Big Data Clustering Algorithm for Mitigating the Risk of Customer Churn,IEEE Transactions on Industrial Informatics, Vol.12, No.3, JUNE 2016, pp.1270-1281.
[14] Christos Boutsidis, Anastasios Zouzias, Michael W.Mahoney, and Petros Drineas, Randomized Dimensionality Reduction for k-Means Clustering, IEEETransactions On Information Theory,Vol.61, No.2, Feb.2015, pp.1045-1062.
[15] Yi Xu Licheng Yu, Hongteng Xu, Hao Zhang,and Truong Nguyen, Vector Sparse Representation of Color Image Using Quaternion Matrix Analysis,IEEE Trans. on Image Processing, Vol.24,No.4, April 2015, pp.1315-1329.
[16] Yong Ning, Xiangjun Zhu, Shanan Zhu, and Yingchun Zhang, Surface EMG Decomposition Based on K-means Clustering and Convolution Kernel Compensation,IEEE Journal of Biomedical And Health Informatics, Vol.19, No.2, March 2015,pp.471-477.
[17] Theo E.Schouten and Egon L.van den Broek,Fast Exact Euclidean Distance (FEED): A New Class of Adaptable Distance Transforms,IEEE Trans. on Pattern Analysis and Machine Intelligence, Vol.36, No.11, Nov.2014, pp.2159-2172.
[18] Mohamed Anis Loghmari, Mohamed Saber Naceur, and Mohamed Rached Boussema, A New Sparse Source Separation-Based Classication Approach,IEEE Trans. onGeoscience and Remote Sensing, Vol.52, No.11, Nov.2014, pp.6924-6936.
[19] Ines Meganem, Yannick Deville, Shahram Hosseini, Philippe Deliot, and Xavier Briottet, Linear-Quadratic Blind Source Separation Using NMF to Unmix Urban Hyperspectral Images,IEEE Trans. on Signal Processing, Vol.62, No.7,April 1, 2014, pp.1822-1833.
[20] Zbynek Koldovsky, Jiri Malek, and Sharon Gannot, Spatial Source Subtraction Based on Incomplete Measurements of Relative Transfer Function,IEEE/ACM Trans. on Audio, Speech,and Language Processing, Vol.23, No.8, August 2015, pp.1335-1347.
[21] P.O.Hoyer, Non-negative matrix factorization with sparseness constraints,J.Mach.Learn.Res.,vol.5, No.1, Jan.2004, pp.1457-469.
[22] Zuyuan Yang, Yong Xiang, Shengli Xie, Shuxue Ding, and Yue Rong, Nonnegative Blind Source Separation by Sparse Component Analysis Based on Determinant Measure,IEEE Transactions on Neural Networks And Learning Systems,Vol. 23, No. 10, October 2012, pp.1601-1610.
[23] Chengjie Li, Lidong Zhu, Zhen Zhang, Non-orthogonal Frequency Hopping Signal Underdetermined Blind Source Separation in Time-Frequency Domain,Infocommunications Journal,vol. 8, No. 3, pp. 1-7, September 2016.
[24] Vaninirappuputhenpurayil Gopalan Reju, Soo Ngee Koh, and Ing Yann Soon, Underdetermined Convolutive Blind Source Separation via Time-Frequency Masking, IEEETrans. on on Audio, Speech, and Language Processing, Vol.18,No.1, Jan.2010, pp.101-116.
[25] Ondrej Tichy and Vaclav Smidl, Bayesian Blind Separation and Deconvolution of Dynamic Image Sequences Using Sparsity Priors,IEEE Trans.on Medical Imaging, Vol.34, No.1, Jan.2015,pp.258-266.
[26] Alex Rodriguez and Alessandro Laio, Clustering by fast search and find of density peaks,Science 344, 1492 (2014), pp.1492-1496.
[27] Guoxu Zhou, Zuyuan Yang, Shengli Xie, and Jun-Mei Yang, Mixing Ma-trix Estimation from Sparse Mixtures with Unknown Number of Sources,IEEE Trans. on Neural Networks, Vol.22,No.2, Feb.2011, pp.211-221.
[28] Vahid Abolghasemi, Saideh Ferdowsi, and Saeid Sanei, Blind Separation of Image Sources via Adaptive Dictionary Learning,IEEE Trans.on Image Processing, Vol.21, No.6, June 2012,pp.2921-2930.
[29] Joel A.Tropp, and Anna C.Gilbert, Signal Recovery From Random Measurements Via Orthogonal Matching Pursuit,IEEE Trans. on Information Theory, Vol.53, No.12, Dec.2007, pp.4655-4666.
[30] D. H. Wolpert and W. G. Macready, No free lunch theorems for optimization,IEEE Trans.Evol. Comput, vol. 1, no. 1, pp. 67–82, Apr. 1997.
[31] Yi Qingming, Blind Source Separation by Weighted K-means Clustering,Journal of Systems Engineering and Electronics, Vol.19, No.5,2008, pp.882-887.
[32] Weihong Fu,Yongqiang Hei, and Xiaohui Li,UBSS and Blind Parameters Estimation Algorithms for Synchronous Orthogonal FH Signals,Journal of Systems Engineering and Electronics,Vol.25, No.6, Dec.2014, pp.911-920.
杂志排行
China Communications的其它文章
- Efficient Subchannel Allocation Based on Clustered Interference Alignment in Ultra-Dense Femtocell Networks
- X-Band Power Amplifier for Next Generation Networks Based on MESFET
- A VMIMO-Based Cooperative Routing Algorithm for Maximizing Network Lifetime
- Efficient Packet Scheduling Technique for Data Merging in Wireless Sensor Networks
- Energy Estimation and Optimization Platform for 4G and the Future Base Station System Early-Stage Design
- A Novel Forwarding Method for Full-Duplex Two-Way Relay Networks
