带管道连接的空间中悬浮铝粉尘爆轰波传播数值模拟

昝文涛, 洪 滔, 董贺飞

(1. 北京理工大学机电学院, 北京 100081; 2. 北京应用物理与计算数学研究所, 北京 100094)

1 引 言

粉尘爆炸是工业生产中常见的事故,2009～2013年我国共发生金属粉尘引发的爆炸共有20起,其中大部分为铝镁粉尘爆炸引起[1]。近年军事领域中温压武器发展迅速,其中铝粉等固体燃料由于其质轻含能高的优点得到越来越广泛的应用,因此研究铝粉尘爆轰在工业安全和军事领域均具有重要意义。

Pawel Kosinski[2]研究了容器中产生的爆轰波通过管道传播进入另一充满粉尘的空间内的数学模型。洪滔[3-4]研究了铝颗粒激波点火机制,模拟了爆轰波管中的铝粉尘爆轰。刘庆明[5]实验研究了管道中铝粉尘在弱起爆条件下的燃烧转爆轰(DDT)过程。韦伟[6]基于CE/SE方法模拟二维管道内铝粉尘爆轰过程。滕宏辉[7]研究了真实比热模型下铝粉尘的两相爆轰波。李鑫等[8]实验研究了不同类型微/纳米铝粉的点火燃烧特性,对比了不同粒径以及不同介质包覆后的铝粉点火延迟时间。

由于条件限制,上述研究大多以爆轰波管实验为主,数值模拟也大多集中在简单的二维平面管道方面,而关于铝粉尘爆轰波在较复杂的几何空间内传播研究较少,无论是工业生产车间,还是巷道等防御工事,其中存在由通风管道或巷道连接的几何空间,在其中的一处发生爆轰后容易通过管道等发生连锁爆炸,造成大范围毁伤破坏,对通过管道连接的空间内铝粉尘的爆轰研究在粉尘爆轰传播及毁伤效应及防护工程中有着重要的实际意义。

为此,本研究采用CE/SE(时-空守恒元解元)算法[9-11]求解两相流模型方程组,对空气中悬浮铝粉尘在管道连接空间内的爆轰进行了数值模拟,对铝粉尘爆轰波的传播过程及爆轰波的绕射等物理过程进行了研究。

2 两相流方程及反应模型

模拟采用了二维两相流模型[12],假设铝颗粒为球形,初始半径都相同,单个颗粒温度均匀,气体中各组分都是均匀混合的,忽略了粒子间的相互作用,不考虑颗粒与气体间的辐射作用,忽略了粒子和固壁间的热传导。

气相方程:

(1)

(2)

(3)

IqAl-Fxu2-Fyv2

(4)

固相方程:

(5)

(6)

(7)

(8)

(9)

组分方程:

(10)

气体状态方程:

(11)

式中,角标1、2分别代表气体和Al。变量ρ为密度,kg·m-3;u为横向速度,m·s-1;v为纵向速度,m·s-1;p为压力,Pa;e为内能,J;φ(φ1+φ2=1)为体积分数,n为单位体积内铝颗粒粒子数;T为温度,K;y为组分浓度,w为分子量。

源项中I为单位体积内铝颗粒的质量变化率,qAl为单位质量的铝颗粒的反应能,J。τ为气体中各组分质量生成率[13],当温度达到或超过Al2O3沸点时,Al2O3会发生分解[14],温度将保持在Al2O3沸点。

对于铝颗粒,采用以下反应模型[15]:

(12)

(13)

式中，Tign为铝粉尘点火温度[2];r2为粒子半径,m;d0为粒子初始直径,m;ψ为气体中氧气的摩尔份数;Fx为气体对粒子在x方向的拖曳力,N;Fy为气体对粒子在y方向的拖曳力,N。

(14)

(15)

拖曳系数:

(16)

Re为雷诺数,Q为气体与粒子间的热传导:

(17)

式中，λ=0.1 J·(m·s·K)-1为气体导热系数[16],Nu为Nusselt数[12],Nu=2+0.459Re0.55Pr0.33，Pr是普朗特数。

通过CE/SE方法求解欧拉方程组,采用四阶龙格库塔方法求解方程组的源项,编制程序模拟爆轰波在二维空间的发展过程。

3 数值模拟结果

3.1 程序验证

为检验程序合理性,模拟了激波管问题,气体密度、压力和速度等进行了无量纲化,初始条件:t=0时刻,

对于理想气体,绝热指数1.4,网格数量200,计算结果如图1所示。

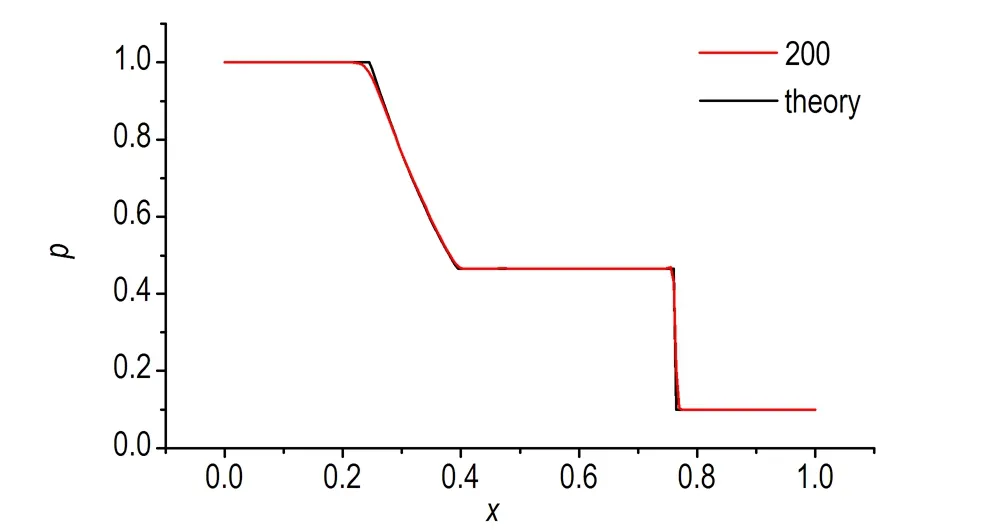
图1t=0.2时刻激波管的压力分布

Fig.1 The pressure distribution of shock tube att= 0.2

由图1可看出,网格数量200时的数值解与理论解符合较好,可以很好地模拟激波管问题。

对铝粉尘与空气当量比为1时在管道内的爆轰波传播过程进行了模拟验证,铝粉尘浓度为0.304 kg·m-3,铝颗粒半径为1.7 μm,爆轰波管直径为15.2 cm。数值模拟得到的爆轰波参数为[17]:D=1.63 km·s-1,ρCJ=2.43 kg·m-3,uCJ=673 m·s-1,pCJ=2.04 MPa,T=3800 K,p=3.31 MPa,与Tulis[18]等由实验中得到的铝粉尘的爆速为1650 m·s-1的结果符合良好。

3.2 计算条件

计算了管道连接空间的二维模拟模型,区域尺寸如图2所示,左侧区域为3 m×3 m空间,除管道出口外均为固壁; 中间管道直径0.2 m,长2 m; 右侧空间3 m×1 m,上下为固壁,右端开口。模拟网格尺寸为5 m×5 m,时间步长Δt=0.2×min(dxdy)/(5×(u1+c)),c为声速。铝粉尘的密度为0.304 kg·m-3,铝颗粒半径为2.0 μm。起爆区域位于左上角,起爆条件为φ1=1,ρ1=2.2 kg·m-3,u=1400 m·s-1,v=-1400 m·s-1,T1=3200 K,该起爆条件是为了符合实验中起爆炸药的质量与能量而确定的。A-Q为数据采集点。

图2 数值模拟区域尺寸模型

Fig.2 Area size model used for numerical simulation

3.3 数值模拟结果

3.3.1 左侧空间中的爆轰波数值模拟结果

图3是数值模拟得到的不同时刻的爆轰波流场压力图。由图3可见,2.36 ms时刻(图3a),由于起爆区域较小位于左上角,爆轰波阵面接近球形,此时爆轰波波阵面同时到达右壁面和下侧壁面发生反射,在固壁处形成的高压区压力达到6.5 MPa; 2.53 ms时刻(图3b),此时爆轰波反射区更明显,爆轰波与空间右侧固壁产生的1号反射波向左传播,爆轰波与空间下固壁产生的2号反射波向上传播,而未发生反射区域爆轰波压力为2.6 MPa,速度为1414 m·s-1,由于传播距离不够长,此时未达到稳定爆轰,爆轰波速度及压力均低于表1中的结果; 3.16 ms时刻(图3c),此时爆轰波到达右下角处,同时爆轰波与右固壁和下固壁产生的1号和2号反射波在此区域交汇形成局部高压区,压力可达18 MPa; 3.90 ms时刻(图3d),此时左侧空间中主要存在四类区域,Ⅰ区为左上角处区域,此次空间为爆轰波后流场; Ⅱ区为右上角和左下角区域,这两部分区域为反射波后流场,右上角区域是1号反射波后形成,左下角区域是2号反射波后形成的; Ⅲ区为对角线中间区域的局部高压区,右上角和左下角区域为1号和2号反射波此时相遇形成; Ⅳ区为位于右下角高压区,是由1号和2号反射波与固壁作用后形成的多次反射波叠加形成的复杂流场。

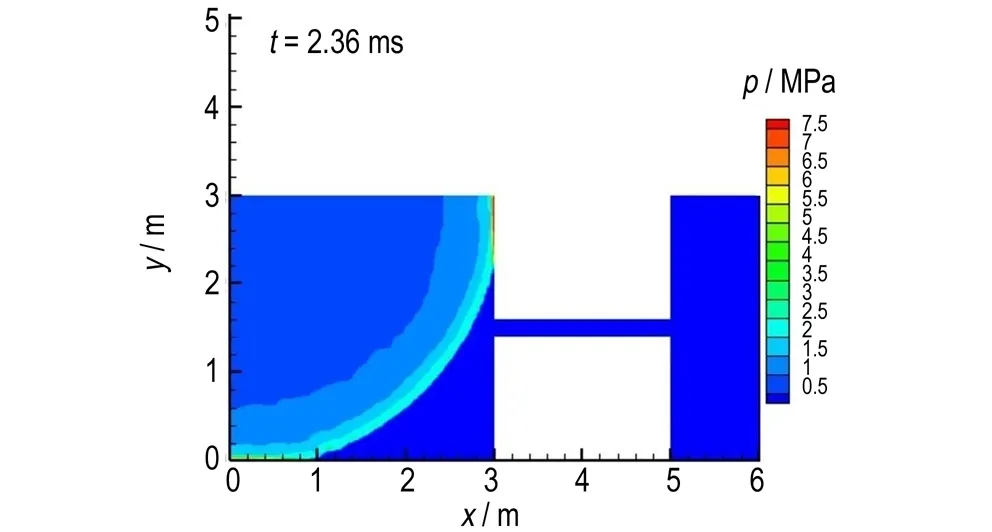
a. 2.36 ms

b. 2.53 ms

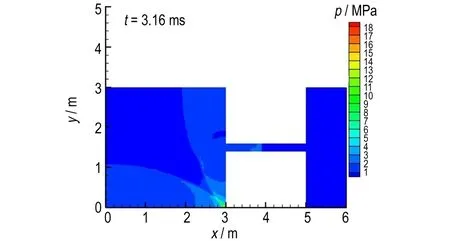
c. 3.16 ms

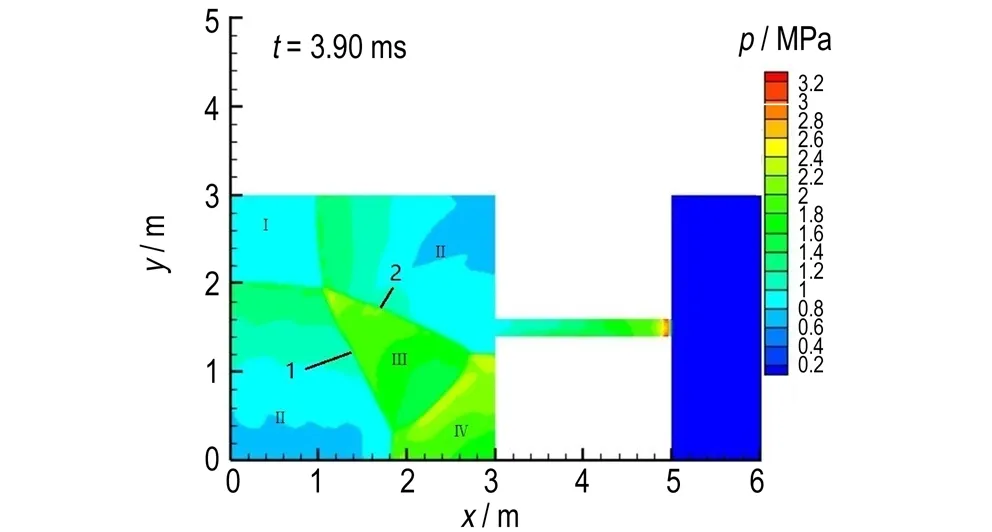
d. 3.90 ms

图3 数值模拟得到的不同时刻的模拟区铝粉尘爆轰波流场的压力分布

Fig.3 Pressure distribution of the aluminum dust detonation wave flow field in simulation area at different time obained by numerical simulation

图4为3.90 ms时刻爆轰波流场的温度分布图。图4中显示在左侧空间内波后流场为3400 K以上的高温。

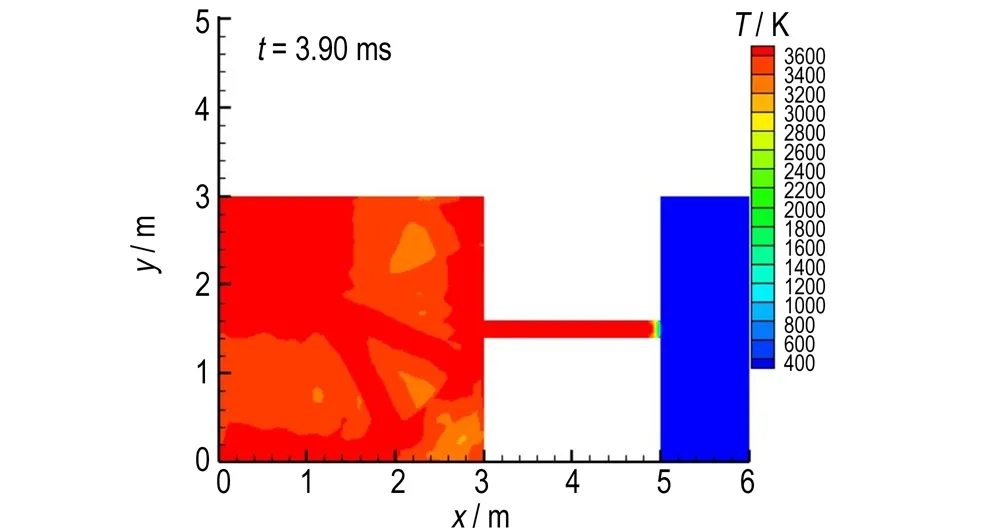
图4t=3.90 ms时刻铝粉尘爆轰波流场的温度分布

Fig.4 Temperature distribution of the aluminum dust detonation wave flow field at 3.90 ms

图5分别为空间中不同数据采集点处的压力随时间变化曲线。图5a中六个点(A,B,C,D,E,F)均匀分布在左侧空间的左上角与右下角斜对角线上,从图5中可以看出在铝粉尘起爆后生成的爆轰波压力不断增长,到达E(2.5,0.5)处时压力达到2.25 MPa,当爆轰波到达F(3.0,0.0)处时,爆轰波与1号、2号反射波相交形成三波点,此时压力跃升到18 MPa,为空间区域压力最高点。而后由1号反射波与下固壁作用产生的1-1号反射波和由2号反射波与右固壁作用产生的2-1号反射波同时到达E(2.5,0.5)点,此时双波叠加压力为4.9 MPa,随着反射波逐渐传播,压力逐渐下降。

图5b为距离左侧空间上固壁处0.5 m处的一排点(A,G,H,I,J)的压力随时间变化曲线,在爆轰向右侧固壁传播,爆轰波波阵面压力逐渐增大,到达J(2.5,2.5)处时压力为2.3 MPa; 在爆轰波与壁面作用发生反射后会生成反射波,反射波经过J(2.5,2.5)时压力为2.1 MPa,而后反射波强度随传播距离增大逐渐降低; 由于1号和2号反射波同时到达A(0.5,2.5)点,因此压力跃升至2.1 MPa,而后可以看出由于2号反射波经过,G-J点压力也会出现跃升并且逐渐降低。从图中可以看出,A点由于反射波的作用,压力还有一次明显的跃升过程。

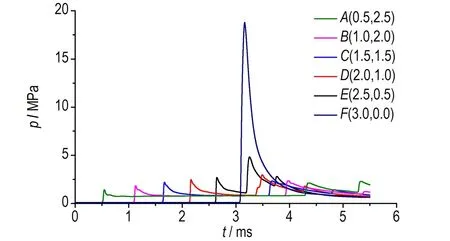
a. pressure at collecting points on the diagonal line at the left side of space

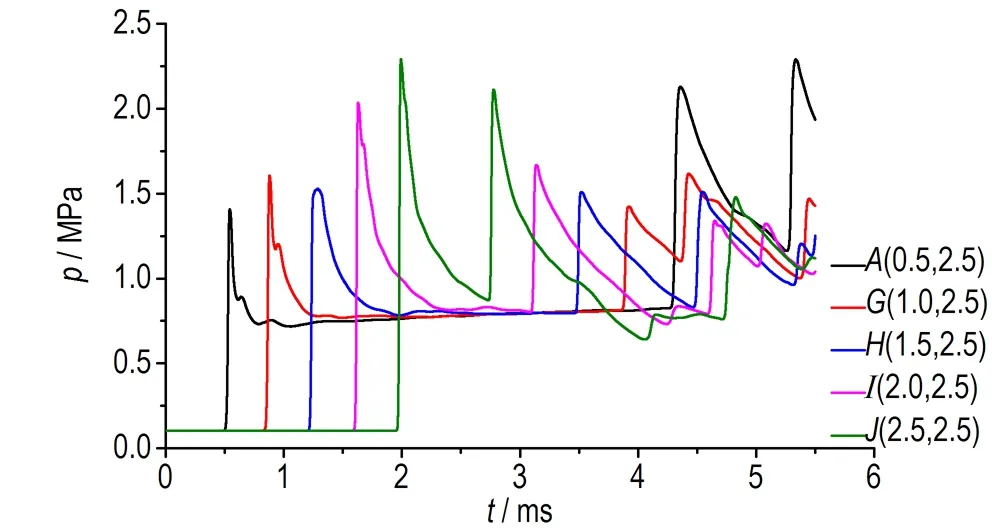
b. pressure at horizontal collection points at the left side of space

图5 不同采集点压力随时间变化

Fig.5 Change in pressure with time at different collecting points

3.3.2 连接管道中爆轰波传播的数值模拟结果

图6为2.62 ms时刻管道入口附近的流场压力图和密度图。右侧的波为进入管道内部传播的初始爆轰波。此时爆轰波沿管道左上角绕射进入管道内部,在管道左上角区域形成低压低密度区域,在管道左下角区域由于爆轰波与固壁作用形成高压高密度区域。3.90 ms时刻爆轰波到达管道出口处,爆轰波波后流场温度从图4中可以看出稳定在3400 K。

图7为沿管道中心线上均匀分布的5个点(K,L,M,N,O)和右侧空间处2个点(P,Q)压力随时间变化,爆轰波到达管道入口时压力为2.6 MPa,在爆轰波绕射进入管道后压力略下降,而后爆轰波继续增长,在到达管道出口处时爆轰波速度为1571 m·s-1,压力达到2.85 MPa。

对比模拟了0.2 m宽管道中铝粉尘的爆轰波传播过程。表1为爆轰波达到稳定时爆轰波参数,模拟得到网格尺寸5 mm时爆速为1591 m·s-1,爆轰波阵面压力3.01 MPa,CJ点气体密度为2.07 kg·m-3,CJ点压力为1.73 MPa,CJ点温度是3794 K,CJ点气体速度为510 m·s-1。

a. pressure nephogram b. density nephogram

图6t=2.62 ms时刻管道入口处流场的压力和密度分布

Fig.6 Pressure and density distributions of the flow field at the entrance of channel at 2.61 ms

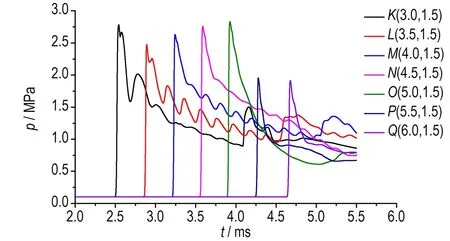
图7 管道中不同采集点压力随时间变化

Fig.7 Change in pressure with time at different collecting points in channel

表1 稳定爆轰波参数

Table 1 Parameters for stable detonation wave

gridsize/mmwavevelocity/km·s-1pressure/MPadensityofCJpoint/kg·m-3pressureofCJpoint/MPatemperatureofCJpoint/KvelocityofCJpoint/m·s-1515702．912．041．713795494

与表1比较发现,管道出口处爆轰波基本达到稳定状态。爆轰波进入右侧空间中爆轰波压力会下降。

3.3.3 右侧空间中的爆轰波传播的数值模拟结果

图8为4.03 ms时刻管道出口附近流场压力分布和密度分布。此时爆轰波离开管道传播进入右侧空间内,爆轰波沿管道上下两个拐角绕射进入大空间内传播,在拐角处形成两个低压低密度区域,此时爆轰波由于绕射的效应,往上下传播的波阵面较弱,因此波阵面后的压力密度较低,往右侧传播的波阵面较强,波阵面后压力密度相对较高。爆轰波阵面的压力和密度沿管道中心轴线成对称分布,呈蘑菇状分布。图9为4.37 ms时刻爆轰波流场的温度分布,爆轰波从管道进入右侧空间后,波后流场温度为3600 K,由于爆轰波绕射,在管道出口处温度比波后流场小,为3000 K。图10为4.62 ms时刻右侧空间内流场压力,此时右侧空间内爆轰波压力为1.9 MPa,速度为1400 m·s-1,在计算区域内未达到稳定爆轰状态。

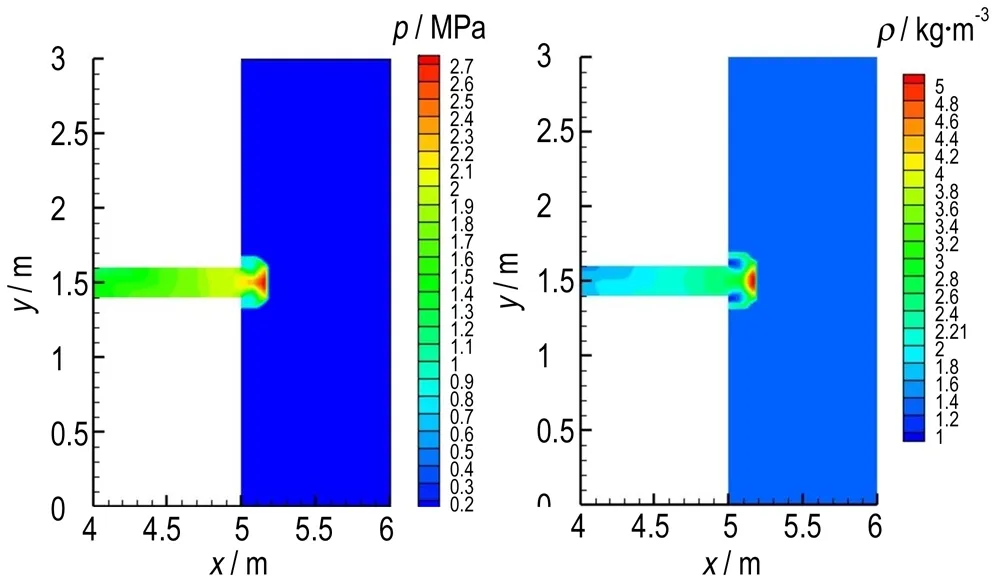
a. pressure distributions b. density distributions

图8t=4.03 ms时刻管道出口附近的压力和密度分布

Fig.8 Pressure and density distributions near the exit of channel at 4.03 ms

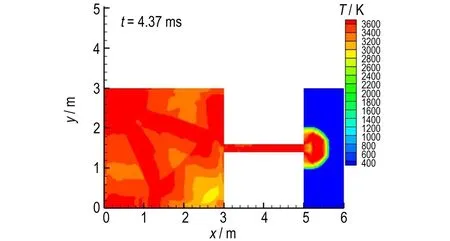
图9 4.37 ms时刻铝粉尘爆轰波流场的温度分布

Fig.9 Temperature distribution of the aluminum dust detonation wave flow field at 4.37 ms

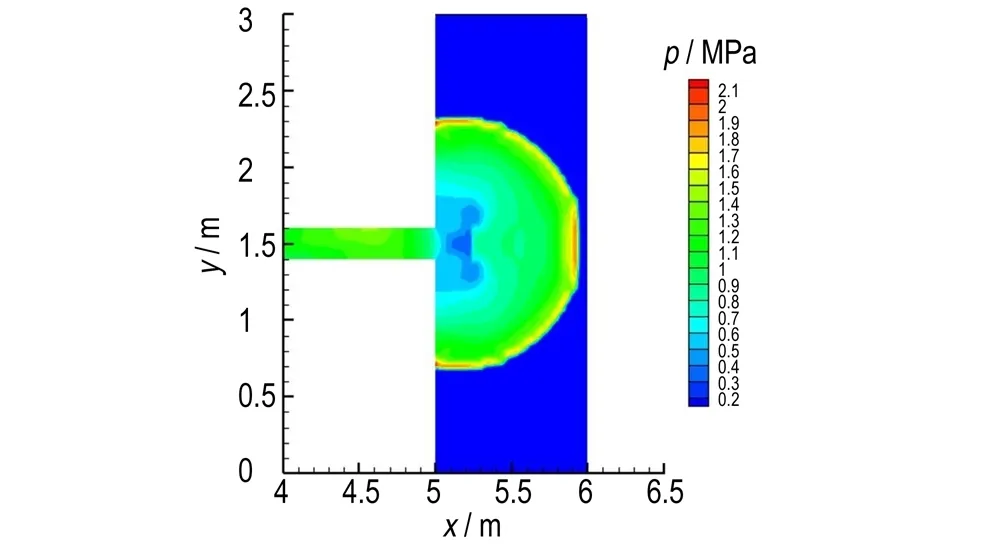
图10t=4.62 ms时右侧空间内流场压力云图

Fig.10 Pressure distributions of the flow field in the right side of space at 4.62 ms

4 结 论

采用两相流模型数值模拟了悬浮空气中的铝粉尘浓度为0.304 kg·m-3,铝颗粒半径为2.0 μm时爆轰波在管道连接的两个大空间内起爆及爆轰波传播过程。得到如下结论:

(1)左侧空间中左上角铝粉尘点火后形成爆轰波在空间内传播,当爆轰波到达固壁处后产生反射波,两个壁面产生的反射波相遇后相互作用在右下角区域交汇形成18 MPa的局部高压区,而后两个反射波随传播会产生交汇形成相互作用区域,同时两个反射波会继续与固壁产生反射形成复杂流场区域。

(2)爆轰波能通过管道入口处绕射进入管道,在管道中传播并在到达管道出口处时爆轰波速度为1571 m·s-1,压力达到2.85 MPa,基本达到稳定传播状态。

(3)在爆轰波绕射后传播进入右侧空间,在管道拐角处产生绕射形成对称低压低密度区域,爆轰波波后区域压力密度分布呈蘑菇状,在计算区域内未达到稳定爆轰。

(4)在整个计算区域内,爆轰波阵面后大部分区域的温度为3400 K以上的高温,仅在管道出口处由于爆轰波发生绕射温度为3000 K。

上述模拟结果反映了铝粉尘爆轰的高温,易传播的特点,以及爆轰波传播过程产生的反射和绕射的效应,为复杂几何形状空间内的铝粉尘爆轰的传播及毁伤效应提供了认识。

参考文献:

[1] 多英全,刘垚楠,胡馨升. 2009～2013年我国粉尘爆炸事故统计分析研究[J]. 中国安全生产科学技术, 2015, 11(2): 186-190.

DUO Ying-quan, LIU Yao-nan, HU Xin-sheng. Statistical analysis on dust explosion accidents occurring in China during 2009-2013[J].JournalofSafetyScienceandTechnology, 2015, 11(2): 186-190.

[2] Pawel K, Alex C. Hoffmann. Dust explosions in connected vessels: mathematical modelling[J].PowderTechnology, 2005, 155: 108-116.

[3] 洪滔, 秦承森. 铝颗粒激波点火机制初探[J]. 爆炸与冲击, 2003, 23(4): 295-299.

HONG Tao, QIN Cheng-sen. Mechanism of shock wave ignition of aluminum particle[J].ExplosionandShockWaves, 2003, 23(4): 295-299.

[4] 洪滔, 秦承森. 爆轰波管中铝粉尘爆轰的数值模拟[J]. 爆炸与冲击, 2004, 24(3): 193-200.

HONG Tao, QIN Cheng-sen. Numerical simulation of dust detonation of aluminum powder in explosive tubes[J].ExplosionandShockWaves, 2004, 24(3): 193-200.

[5] LIU Qing-ming, LI Xiao-dong, BAI Chun-hua. Deflagration to detonation transition in aluminum dust-air mixture under weak ignition condition[J].CombustionandFlame, 2009,156: 914-921.

[6] 韦伟, 翁春生. 基于CE/SE方法的铝粉尘爆轰二维两相数值计算[J]. 弹道学报, 2012, 24(4): 99-102.

WEI Wei, WENG Chun-sheng. Two-dimension two-phase-flow numerical simulation of aluminum-dust detonation based on CE/SE method[J].JournalofBallistics, 2012, 24(4): 99-102.

[7] 滕宏辉, 杨旸, 姜宗林. 真实比热模型中铝粉尘两相爆轰波的数值研究[J]. 计算物理, 2013, 30(1): 44-52.

TENG Hong-hui, YANG Yang,JIANG Zong-lin. Realistic heat capacity effects in two phase aluminum dust detonations[J].ChineseJournalofComputationalPhysics, 2013, 30(1): 44-52.

[8] 李鑫, 赵凤起, 郝海霞, 等. 不同类型微/纳米铝粉点火燃烧特性研究[J]. 兵工学报,2014, 35(5): 640-647.

LI Xin, ZHAO Feng-qi, HAO Hai-xia, et al. Research on ignition and combustion properties of different micro/nano-aluminum powders[J].ActaArmamentaril, 2014, 35(5): 640-647.

[9] Chang S C. The method of space-time conservation element and solution element-a new approach for solving the navier-stokes and euler equations[J].JournalofComputationalPhysics, 1995, 119(2): 295-324.

[10] Zhang D L, Wang J T, Wang G. High-order CE/SE method and applications[J].ChineseJournalofComputationalPhysics, 2009, 26(2): 211-220.

[11] Wang J T, Zhang D L, Liu K X. A eulerian approach based on CE/SE method for 2D multimaterial elastic-plastic flows[J].ChineseJournalofComputationalPhysics, 2007, 24(4): 395-401.

[12] 方丁酉. 两相流体力学[M]. 国防科技大学出版社. 1988: 117-129.

[13] 洪滔, 秦承森, 林文洲. 悬浮RDX炸药和铝颗粒混合粉尘爆轰的数值模拟[J]. 爆炸与冲击, 2009, 29(5): 468-473.

HONG Tao, QIN Cheng-sen, LIN Wen-zhou. Numerical simulation of detonation in suspended mixed RDX and aluminum dust[J].ExplosionandShockWaves, 2009, 29(5): 468-473.

[14] Steinberg T A, Wilson D B, Benz F. The combustion phase of burning particle[J].CombustionandFlame, 1992, 91(2): 200-208.

[15] Price E W. Combustion of metalized propellants[A].ProgressinAstronauticsandAeronautics:FundamenalsofSolid-PropellantCombustion, AIAA,New York, 1984, 90: 479-513.

[16] 杨世铭, 陶文铨. 传热学[M]. 高等教育出版社. 2006: 559.

[17] 昝文涛, 洪滔, 董贺飞. 基于CE/SE方法关于RDX-AL悬浮粉尘在空气中的两相爆轰的数值模拟[J]. 爆炸与冲击, 2016, 36(5): 603-610.

ZAN Wen-tao, HONG Tao, DONG He-fei. Numerical simulation of two phase detonation of suspending RDX-AL dust in air with CE/SE method[J].ExplosionandShockWaves, 2016, 36(5): 603-610.

[18] Tulis A J, Selman J R. Detonation tube studies of aluminum particles dispersed in air[C]∥19th International Symposium on Combustion.The Combustion Institute, 1982: 655-663.