UTM投影坐标系下厂站工程坐标系统设计

高春林，孙浩玉

(1.国核电力规划设计研究院，北京 100095；2.山东电力工程咨询院有限公司，山东 济南 250013)

UTM投影坐标系下厂站工程坐标系统设计

高春林1，孙浩玉2

(1.国核电力规划设计研究院，北京 100095；2.山东电力工程咨询院有限公司，山东 济南 250013)

随着国家“一带一路”战略的推行，大量企业开始走出国门承担海外工程，与我国高斯投影坐标系统不同，许多国家采用UTM投影坐标系统，本文通过对UTM投影坐标系下长度变形的分析，以及对厂站工程坐标系统的理解，探讨了一种国外基于UTM投影坐标系统下电厂及变电站工程坐标系统设计方法，并通过赞比亚3个变电站工程实例说明了这种方法的应用。

国外工程；UTM投影；工程测量；投影长度变形。

1 概述

随着国家“一带一路”战略的推行，大批中国企业走出国门承包海外工程，与我国采用高斯投影坐标系统不同，国外许多国家地图投影采用通用横轴墨卡托投影(Universal Transverse Mercator，UTM)，UTM投影坐标系统下工程坐标系统设计是当前许多出外企业面临的主要测量技术问题，国外工程业主一般要求测量采用当地UTM投影坐标系统，而设计人员要求测量满足国内规范精度要求。一些工程由于UTM投影长度变形相对较大(不足1/10000)，满足不了国内工程测量规范“测区内投影长度变形不大于2.5 cm/km”的要求。工程坐标系统如何设计，才能既满足业主的要求，又满足我国基于高斯投影的工程测量规范要求？国内，厂站工程坐标系统常采用抵偿高程面的方法，但由于UTM投影与高斯投影特点不同，国内惯用的抵偿高程面的方法在UTM投影坐标系下并不完全适用。本文通过分析UTM投影与高斯投影长度变形的特点，并通过对厂站工程坐标系统的理解，探讨了一种国外基于UTM投影坐标系统下电厂及变电站工程坐标系统设计方法。

2 UTM投影与高斯投影长度变形特点

UTM投影是一种等角横轴割圆柱投影，圆柱割地球于南纬80°、北纬84°两条等高圈，投影后两条相割的经线上没有变形，而中央经线上长度比为0.9996。这种投影的长度变形限制在1/1000(平均长度变形约为4/万=1/2500)之内。这样既保持了正形投影的性质又改善了变形分布，因而被世界上许多国家所采用，见图1。

图1 UTM投影示意图

UTM及高斯投影变形主要包括两项：地面水平距离投影到参考椭球面的长度变形，以及参考椭球面上的边长投影到UTM投影面的长度变形。其中，地面水平距离投影到参考椭球面的长度变形，UTM投影与高斯投影一样，其1 km长度变形ΔS1约为：

式中：Hm为测距边高出参考椭球面的平均高程；R为测距边所在法截线的曲率半径。由公式可以看出，该变形值恒为“负”。

参考椭球面上的边长投影到投影面的长度变形，UTM投影与高斯投影不同，参考椭球面上1 km长度投影到UTM投影面上的变形ΔS2约为：

而参考椭球面上1 km长度投影到高斯投影面上的变形ΔS2约为：

式中：ym为归算边两端点横坐标平均值；Rm为参考椭球面平均曲率半径。

如果地面水平距离投影到参考椭球面的长度变形ΔS1暂不考虑，由公式(2)及(3)，参考椭球面上的边长投影到投影面的长度变形ΔS2与横坐标Y对应关系见图2，从图上可以看出，UTM投影与高斯投影变形的特点(在南纬15°附近)。

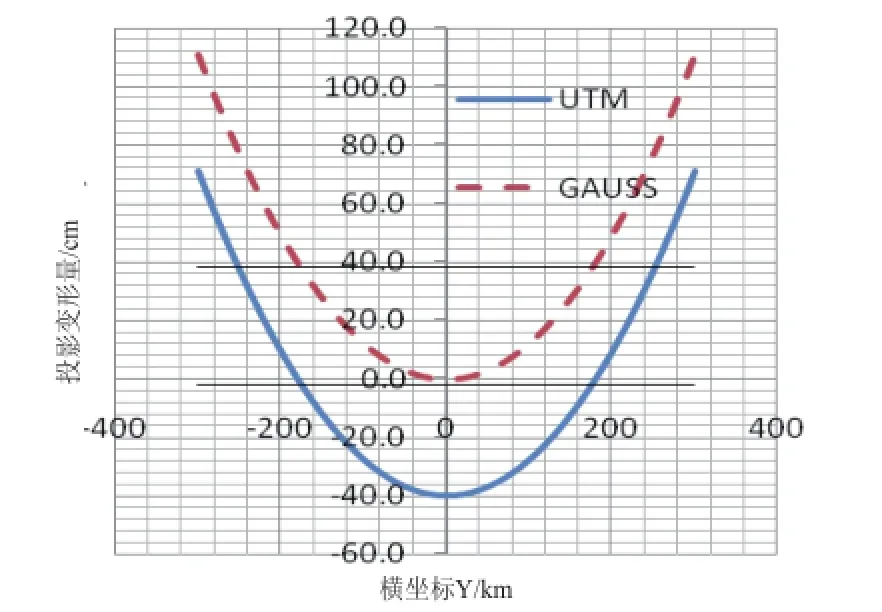
图2 UTM与GAUSS投影变形图

UTM投影和高斯投影的变形值均呈对称型，但高斯投影变形均为正值，且离中央子午线越远变形越大，而UTM投影在中央子午线处负变形值最大，离中央子午线越远负变形越小，直到东西各约180.3 km(约1°45′)的两条割线上，投影变形值为0，离开这两条割线越远则正变形值越大。

UTM投影中央子午线上变形值最大约－40 cm/km，在[－180.3 km，180.3 km]区域UTM投影变形值与参考椭球面变形“同号”，而高斯投影所有区域的变形与参考椭球面变形“反号”。

UTM投影在[174.7 km，185.9 km]，[－185.9 km，－174.7 km]区域变形量不超过2.5 cm/km，即经差[1°42′，1°49′]，[－1°49′，－1°42′]两区域带宽之和总共不超过22.4 km，而高斯投影变形量不超过2.5 cm/km的带宽约为90 km。

如果考虑地面距离投影到参考椭球面的长度变形，由于其长度变形为负值，对于UTM投影，中央子午线东西各约180 km范围内变形值也为负，两者叠加，变形值为“负”的范围会更大。而对高斯投影，两者叠加，变形值会抵消一部分，总变形值降低。所以，国外UTM投影坐标系下工程坐标系统设计，大范围区域内采用国内惯用的抵偿高程面的方法是不可行的。而对高斯投影坐标系统，任何区域可通过改变高程投影面来抵偿投影长度变形。

3 对厂站工程坐标系统的理解

(1)工程平面坐标系统应以满足工程设计及施工为主要目的，厂站工程坐标系统可以不为严格意义上的国家统一坐标系统。

工程测量规范规定：平面控制网的坐标系统，应在满足测区内投影长度变形不大于2.5 cm/km的要求下，可采用国家统一的平面直角坐标系统；或采用抵偿高程面或测区平均高程面的平面坐标系统，任意带的平面坐标系统；小测区或有特殊精度要求的控制网，可采用独立坐标系统；厂区内可采用建筑坐标系统。工程范围内投影变形大于2.5 cm/km的情况下，工程坐标系统可以不采用国家统一坐标系，而采用自定义工程坐标系统。

(2)厂站工程坐标系统投影面应建立在测区平均高程面上或设计施工高程面上。

工程平面坐标系统是为工程设计和施工服务的，厂站工程是建造在实际地表面上的，严格讲是建造在设计场平标高面上的，而不是建造在基于椭球面的投影面上，工程设计及施工建造都要求由坐标反算的距离与实地丈量的距离尽量一致，不要再有换算关系，工程坐标系统投影面选择测区平均高程面或设计零米高程面，符合实际，而且，厂站工程占地面积相对较小，一般不超过50 km2，其区域范围内可以不考虑曲面问题，而以平面考虑。

(3)工程坐标系统设计内符合精度是第一位的，其次才是外符合精度。内符合指各控制点之间相对位置关系符合性强，内符合要求各点之间相对关系满足规范要求。既由控制点坐标反算的边长与实测平距相对误差小于1/20000，外符合指控制点绝对位置的准确性，外符合一般用于本工程定位，以及本工程与当地其他规划之间的联系。工程坐标系统的外符合精度要求相比内符合精度要低得多。

4 UTM坐标系统下工程坐标系统设计

4.1 设计原则

(1)基本原则：由控制点平面坐标反算的边长应与实测平距相接近，即由边长的高程归化及UTM投影归化共同引起的总长度相对变形值应小于1/40000。

(2)按长度投影相对变形决定能否采用国家统一平面坐标系统

根据工程所在地的经纬度，分析采用国家统一UTM投影坐标时总的长度相对变形情况，如果长度相对变形满足规范1/40000精度要求，工程坐标系统可采用当地国统一的平面直角坐标系统；如果长度变形值不满足1/40000精度要求，工程坐标系统可采用自定义工程独立坐标系统。

(3)尽可能采用与国家绝对坐标差异较小的坐标值

工程平面坐标采用与国家绝对坐标差异较小的坐标值，便于与其他基于国家统一平面坐标系统的资料大致统一，便于工程内外部之间的联系。

4.2 确定工程平面坐标系三大要素

投影面(亦即边长归算的高程基准面)的高程、中央子午线的经度、起始点坐标及起始方位角是确定工程平面坐标系的三大要素。投影面的选择：如果工程所在地满足规范对投影长度相对变形的要求，工程平面坐标系应采用国家统一平面直角坐标系，投影面取国家参考椭球面，其他及小测区工程平面坐标系可采用测区平均高程面为投影面；中央子午线经度的确定：中央子午线经度可按工程所在地国家统一分带所确定的中央子午线经度，即选择与国家统一平面坐标一致的中央子午线经度，这样，可保证工程坐标与国家点坐标差异尽可能小；起始点坐标及起始方位角：起始点坐标可取一国家控制点坐标，起始方位角可取起始点到另一国家点的坐标方位角，不顾及两国家点之间方位角固有偏差，使工程独立坐标系的坐标纵轴与国家坐标纵轴相重合(或平行)，这样，工程平面坐标系与国家坐标系的差异主要在于边长尺度的不同。

4.3 工程平面坐标系设计的实现

工程中，平面坐标系设计是在工程控制网平差中具体实现的。具体操作上，第一步，计算工程所在地投影相对变形，确定工程平面坐标系投影面高程，长度相对变形依据高程归化及UTM投影面归化公式计算，根据测区长度相对变形是否超过1/40000判断工程平面坐标系是采用国家平面坐标系还是采用自定义工程坐标系，然后，再根据工程选择的坐标系确定工程投影面高程；第二步，选择起算数据，根据已知点联测情况，选择兼容性较好离测区较近的两个已知点，采用一个已知点坐标，一个由两已知点坐标反算的起始方位角作为控制网平差的起算数据；第三步，观测值的归化计算，如果采用国家平面坐标系，边长需进行高程归化及UTM投影面归化计算，将观测值归化到UTM投影平面上，如果采用工程独立坐标系，边长观测值只归算到测区平均高程面上。第四步，网平差及精度评定，根据选定的起算数据及归化后的观测数据，按平面几何网进行平差计算，得到未知控制点坐标及精度情况，如果控制网中包含其他已知国家点，可比较平差结果与已知坐标的差异情况，进而可分析出工程坐标与国家坐标的接近程度。最后，对平差出的控制点坐标成果进行检查验证，验证控制点间由坐标反算的距离与用仪器测量的距离是否相接近，是否满足工程平面坐标系设计的基本原则。

5 工程实例

赞比亚国家地图投影采用UTM投影，坐标基准采用 ARC 1950，椭球为Clark 1880 modified ellipsoid。赞比亚330 kV输变电工程位于赞比亚北方省内，线路全长约387 km，共设计Pensulo、Mpika、Kasama 3个330 kV变电站，各变电站概略位置及UTM投影长度变形如表1，三站址的UTM投影变形均超过2.5 cm/km的工程测量规范要求。

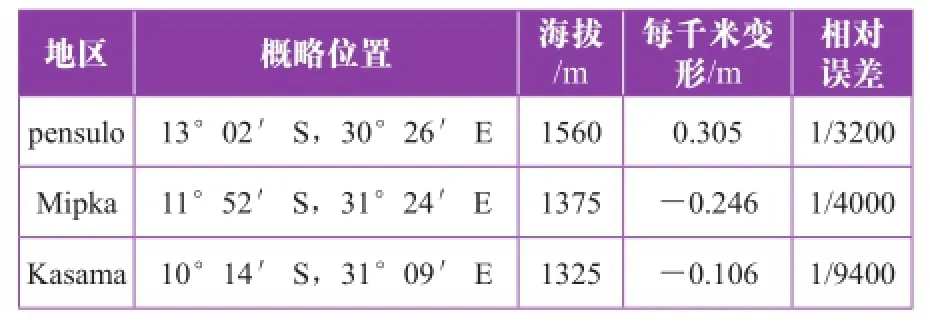
表1 变电站位置及UTM投影长度变形

由表1，该工程三个变电站UTM投影长度相对变形不满足工程测量规范的要求，三个变电站的平面坐标系采用独立平面坐标系。投影面选择测区平均高程面，并以此为控制网平差的投影面，中央子午线经度选择与国家坐标一致的中央子午线经度，起算数据采用一点一方位，比如：Pensulo变电站，投影面选择1560 m测区平均高程面，中央子午线选择33°E，工程控制网联测两个已知点PS1，PS2，起算数据采用PS1及PS1至PS2的方位，GPS基线解算得到的基线向量经高差改正计算出平距，由于Pensulo变电站地形起伏不大，测区平均高程面与控制点高程面差别很小(小于5 m)，边长平面高程面的归化值很小，故忽略不计，控制网平差采用科傻GPS平差软件进行，采用一点一方位方式，投影面选择1560 m，平差完成后，利用全站仪进行检查验证，其验证结果如表2，由表2可知，由坐标反算边长与实测边长接近，边长相对误差最大1/73000，满足规范对工程坐标系统要求。

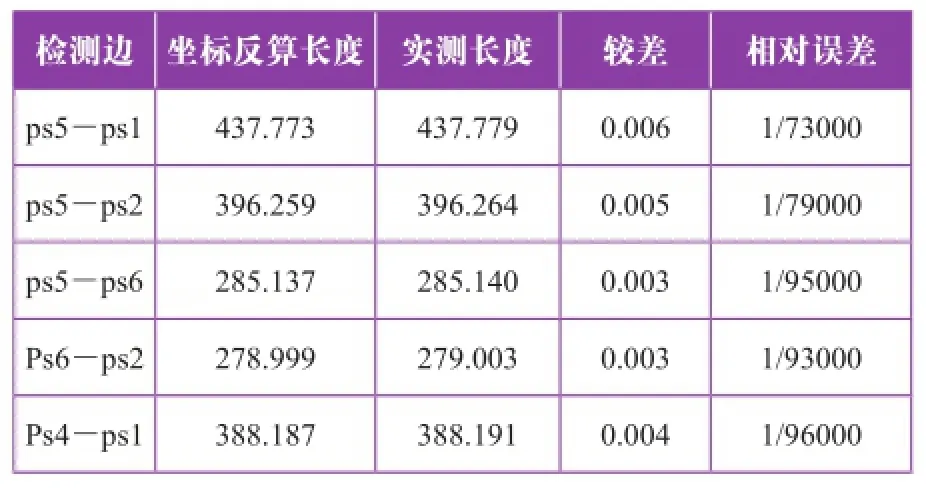
表2 变电站位置及UTM投影长度变形 (单位：m)

6 结语

工程坐标系统设计应首先满足工程测量规范及施工放样要求，以保证工程质量安全。本文通过对UTM投影长度变形的分析以及对厂站工程坐标系统的理解，探讨了一种国外基于UTM投影坐标系统下电厂及变电站工程坐标系统设计方法。另外，根据作者国外工程经验，国外许多国家和地区，尤其是欠发达地区，测量基础设施差，控制点比较少，已知点的精度也不高，限于条件，工程测量控制点坐标不可能做到精度很高，其实，也没必要做得精度很高，满足工程设计及施工要求就好。

[1] 张凤举，张华海．控制测量学[M]．北京：煤炭工业出版社，1999．

[2] 孔祥元，梅是义．控制测量学(下册)[M]．武汉大学出版社，2002．

[3] 刘明波，雷建朝．UTM投影及投影变形处理[J]．西北水电，2010，(6)．

[4] 叶达忠，谢家业．国际工程测量的UTM投影变形及抵偿分析[J]．广西师范学院学报(自然科学版)，2009，(3)．

[5] 袁小勇，陈功.国际工程中UTM投影变形的应对策略—以苏丹某电厂为例[J]．工程勘察，2010 ，(5)．

[6] 王俊，等．毛里塔尼亚努瓦克肖特新国际机场控制测量[J]．勘察科学技术，2008，(3)．

Design of Coordinate System of Power-plant and Substation Engineering under the UTM Projection Coordinate System

GAO Chun-lin1, SUN Hao-yu2
(1.The State Nuclear Electric Power Planning Design & Research Institute, Beijing 100095, China; 2.Shandong Electric Power Engineering & Consulting Institute, Jinan 250013, China )

With the implementation of the national " One Belt and One Road " strategy, more and more enterprises begin to undertake overseas projects,It is different from our Gauss map projection, overseas many countries use UTM projection coordinate system, Based on the analysis of the UTM and GAUSS projection deformation, and the thinking of the plane coordinate system in the power-plant and substation engineering, the paper explores a design method of plane coordinate system based on UTM projection coordinate system in overseas power-plant and substation engineering，and illustrates the application of the way by three substation examples in the 330 kV power line engineering in Zambia.

the overseas engineering; UTM projection; the power plant and transferormer substation survey; projection deformation.

P2

B

1671-9913(2017)02-0007-04

2016-04-10

高春林(1972- )，男，山东德州人，硕士，高级工程师，主要从事电力勘测信息化智慧化研究。