均值不等式的应用初探

李昊冉

摘要：均值不等式在诸多领域都投入了应用，并且占据了重要的地位，同时，均值不等式的应用无论是在初中高中阶段，还是在高等数学阶段，应用都是难点问题，并且在实际生活中的数量关系也更为普遍。不等式与方程、导数、函数等知识点密切相关，在研究函数的值域、定义域、最大值最小值、单调性方面发挥着重要的作用。本文将着重探讨均值不等式的应用，从值域、定义域等方面入手。

关键词：数量关系；均值不等式；应用

在实际的生活中，不等式中的数量关系比相等关系更为普遍。可以说成：相等是相对关系，而不等式是绝对的关系。不等式与各类数学知识点都有密切的关联，在数学领域发挥着重要的作用，占据着重要的地位，我认为均值不等式在数学的学习中起到了十分关键的作用。通过均值不等式的学习，我认为均值不等式在解决疑难问题上面发挥着重要作用，我将根据学习中均值不等式的应用，从函数的值域、定义域、最值、单调性等方面举实例进行分析。

一、均值不等式定理

均值的定理即是：如果a、b∈R+，则有（a+b）/2≥√ab，同时当a=b时，则等号成立。由此可知，两个正实数的算术平均值大于或者等于其几何平均值；或者可以说成是两个正实数的等差中项大于或等于其等比中项，就几何意义来说可以说成是半径大于等于半弦。可以看出最值的定理是：a>0，b>0，当a+b=S时，S为定值，则在a=b时，ab存在最大值，最大值是S2/4；ab=S时，S为定值，则在a=b、a+b时存在最小值，最小值为2√S。从定理可以得出，均值不等式的应用需要三个必备条件：一正、二定、三相等，则要求在应用均值不等式时必须要保证数、和式子是正数，并且满足大于零的条件，才不会出现误解的问题[1]。

二、均值不等式的应用例题

1、求最值。我认为应用均值不等式求最值在高中的数学教学中属于重点内容，在上文中详细叙述了均值不等式的应用条件，因此，在求最值中应用均值不等式主要会使用以下三种方式：巧妙变形求最值法、直接求最值法、结合待定系数求最值法。以下则通过实际例题进行说明：

例题1：已知2b2-a2= 1，求y=∣a-2b∣的最小值。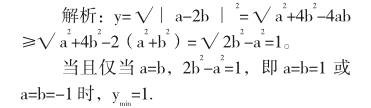

综上例题所述，在均值不等式的应用中，首先我们要了解其几何原理，并且对其理论要有详细的理解，才能够使得解题的方式更加通透，能够更加直观的看到结果，以此更快更好的掌握题型。同时，可以加强相应的探究空间，将思考集中起来，变得更加细致缜密，才能够准确的得出答案。其次，在学习过程中我们要重视均值不等式的应用，增加独自解题的次数，才能够对各类题型有所掌握，更好的解决问题，才能够通过加强学习来锻炼我们解决问题的能力[2]。

例题2：求解函数y=sinX+（4/ sinX），X∈（0，π/2]的最小值。

分析：我认为在应用均值不等式求解题目时，对于不同的题型是有不同的解题方法的，所以在解题之前必须要清楚提醒是否能够满足均值不等式的使用条件，再来选择解题方法，才能够有效避免解题误区。

错解：因为X∈（0，π/2]，所以sinX>0，4/sinX>0。

则有y=sinX+（4/sinX）≥√sinX×4/ sinX=4，所以sinX=2.

从解题中可以知道，当sinX=2时，不等式是不成立的，因此该题不能适用均值不等式解题，正确的解题方式应该是应用函数的单调性来解答。

正解：因为X∈（0，π/2]，所以0

所以0

又因为y'=1-4/T2，0

所以y=T+4/T，在（0，1]区间上是单调递减的函数，ymin=5，则有T=1，即是sinX=1，X=π/2.

2、求值域。

例题3：求函数y=x+1/x，（x≠0）的值域。

错解：y=x+1/x≥2√x·1/x=2，因此函数的值域是（2，+∞）

分析：出现错解的问题是非常普遍的，所以在運用均值不等式时必须要注重解题条件，该题必须要将当x<0转变成x>0。

正解：当x>0，y=x+1/x≥2√x·1/ x=2，x<0，则-x>0，

所以y = x + 1 / x =（- x + 1 / - x）≤-2√-x·1/-x=-2.综上所述，即是函数 y=x+1/x，（x≠0）的值域是（-∞，-2]∪[2，+∞）。

由此可见，在应用均值不等式时成立条件是必备的解题因素。

三、均值不等式的应用注意事项

在均值不等式的应用中，由于不同的均值不等式对于实数的取值范围不同，所以在应用中要求也不同，比如说当实数处于二次根号以下，则要求实数是大于或等于零的。其次均值不等式的使用目标是针对带有等号的不等式，并且在解答问题时，需要满足均值不等式的三个成立条件，才能够顺利的完成解题。然后，作为学生，需要掌握解题方法、解题技巧，才能在解题过程中如鱼得水更好的完成作业，同时，我在学习过程中，为了能够更快掌握学习技巧会使用如下方式代替数值：用符号、图形、生活相关的用语等。将语言用符号代替，可以更加明确的展现出数、式与均值不等式的关联

[3]。同时在比较圆的直径和弦长时，也可以使用均值不等式求解，将均值不等式的几何意义表达出来，在数学的实际应用中发挥着重要作用。最后，在所有周长相同的全部矩形中，面积最大的那个即是正方形。而在所有面积相同的全部矩形中，周长最小的那个即是正方形。由此可知，数学需要我们不断的分析和论证，才能够帮助我们更快更准确的解答问题。

四、结语

均值不等式在中学的学习中，不仅是重点内容，也是难点，但是它的应用范围广泛，尤其是在函数的最值求值上。在利用均值不等式求值时，其成立条件：“一正、二定、三相等”具有重要作用。虽说如此，但是在实际的解题应用过程中，依然会随时出现问题，此时便要针对题目进行分析，找出合适的解题方法，来提高自身对于均值不等式的认识。同时，要根据自身的学习情况，根据自身对均值不等式的理解，学习举一反三的数学知识运用，不断提高自身学习能力。

参考文献

[1] 王冬梅. 浅谈均值不等式的应用[J]. 科教导刊（上旬刊），2014，04：64-65.

[2] 王琳，杨秀. 广义均值不等式及其简单应用[J]. 四川理工学院学报（自然科学版），2015，03：96-100.

[3] 潘伟云. 均值不等式的探讨[J]. 吕梁教育学院学报，2016，01：96-97.