基于Park-Ang损伤指标的规则桥梁概率地震需求分析
2017-05-04曾武华张仁巍王逢朝卓卫东
曾武华,张仁巍,王逢朝,卓卫东
(1.三明学院 建筑工程学院,福建 三明 365004;2.福州大学 土木工程学院,福建 福州 350116)
基于Park-Ang损伤指标的规则桥梁概率地震需求分析
曾武华1,张仁巍1,王逢朝1,卓卫东2
(1.三明学院 建筑工程学院,福建 三明 365004;2.福州大学 土木工程学院,福建 福州 350116)
采用增量动力分析的方法,选择基本周期处谱加速度作为地震动强度指标,Park-Ang损伤指标作为工程需求参数,建立规则桥梁结构概率地震需求模型。结果表明:在给定地震动强度水平下,Park-Ang损伤指标服从正态分布,通过回归分析给出了工程需求参数与地震动强度指标之间的关系。最后,应用该概率地震需求模型对一座实例桥进行地震需求危险性分析,验证了该方法的实用性。
基于性能抗震设计;规则公路桥梁;概率地震需求模型;增量动力分析;Park-Ang损伤指标
基于强度设计方法是目前各国规范对于规则桥梁抗震设计和验算普遍采用的设计方法。结构在小震作用下一般要求保持弹性状态,对于这一阶段基于强度设计是可以适用的。但是,对于强烈地震动作用下,要求结构处于弹性状态是不经济也不实际的[1]。基于性能抗震设计是美国学者和工程师率先提出的先进的抗震设计思想,允许结构在强烈地震动作用下进入弹塑性阶段,并采用损伤指标对结构产生的损伤程度进行量化[2]。Park-Ang损伤指标是在大量钢筋混凝土构件试验结果分析基础上提出的,考虑了变形和能量组合的综合性能指标,被各国学者广泛采用[3]。尤其在基于性能抗震设计思想受到国际抗震工程界广泛重视与研究的背景下,Park-Ang损伤指标作为结构损伤最实际的衡量指标之一,成为研究者关注热点[4-6]。在地震作用下,Park-Ang损伤指标的需求计算是抗震设计关键部分。杨伟和欧进萍[7]从能量关系入手,利用结构滞回耗能与结构最大位移的关系,给出Park-Ang损伤指标的简化计算方法。一些研究者[8-9]采用基于损伤的弹塑性反应谱,计算结构在地震作用下的损伤指标需求。由于地震动和结构特性的随机性,学者普遍认为地震需求的计算需要采用概率分析的方法[10-12]。本文考虑地震动的随机性,对8座规则桥梁样本进行非线性动力时程分析,得到其地震动强度指标与工程需求参数之间的关系曲线。在给定地震动强度指标下,采用概率统计的方法分析各桥梁样本的Park-Ang损伤指标的概率分布;并通过回归分析,建立Park-Ang损伤指标的概率统计特征值与地震动强度指标的关系。
1 规则桥梁及结构有限元模型
本文的研究对象是公路桥梁中的规则桥梁,现行的《公路桥梁抗震设计细则》给出了规则桥梁的具体规定[13]。对8座规则桥梁结构样本进行分析,基准桥结构形式如图1所示。该基准桥为一座4跨一联钢筋混凝土规则连续梁桥,桥跨组合为4×18 m,除了在其中的一中墩上设置固定支座外,其余墩(台)均为滑动支座。下部结构采用圆形截面独柱式桥墩,直径为1.6 m,纵向钢筋配筋率为1.2%,箍筋的配箍率为0.8%。其余7座桥梁样本通过改变基准桥梁的长细比和轴压比,从而得到不同基本周期的桥梁样本。根据规则桥梁的特点,在进行结构地震反应分析时,通常可以把其简化为所谓的“单墩模型”[13],如图2所示。采用OpenSees软件建立其有限元数值分析模型,上部结构采用质量模拟,桥墩采用弹塑性纤维梁柱单元模拟,混凝土材料采用concrete04模拟,其本构关系参数通过Mander模型计算,钢筋材料采用reinforcingsteel模拟[14]。8座典型桥梁样本基本参数如表1所列。
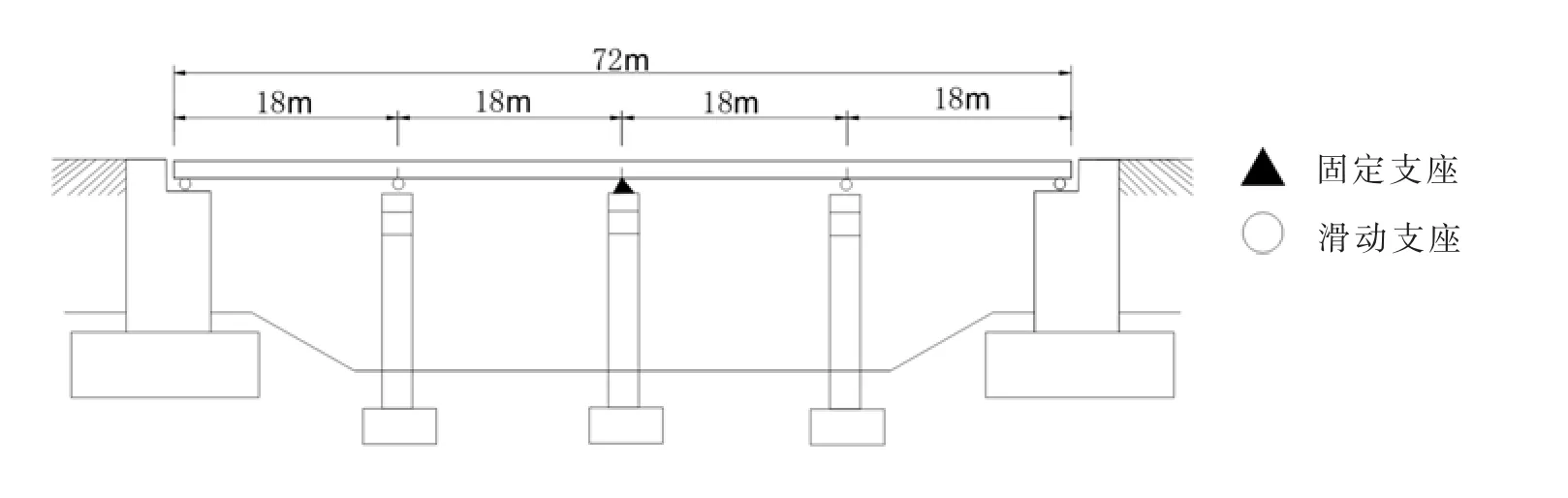
图1 公路规则桥梁基准桥结构形式

图2 典型桥梁样本简化单墩模型
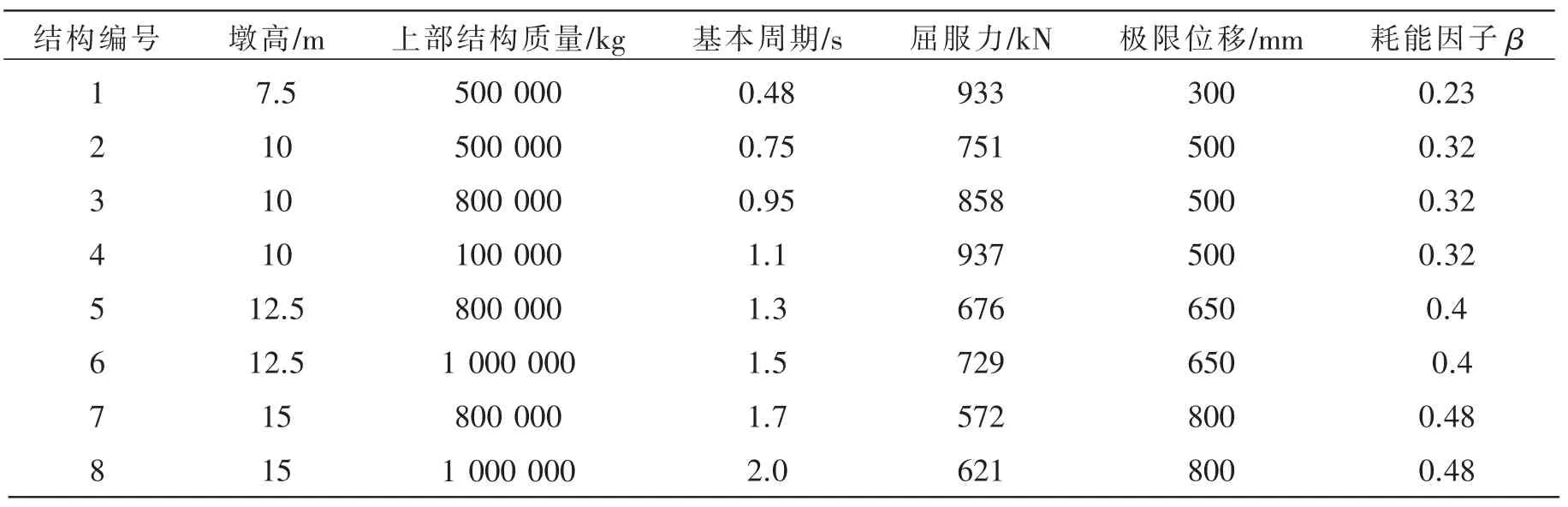
表1 典型桥梁样本基本参数
2 增量动力分析
2.1 地震记录
为充分考虑地震动记录的随机性,本文搜集了国内外共2390条水平方向强震时程记录。其中Ⅰ类场地水平地面运动记录514条,Ⅱ类场地1214条,Ⅲ类场地662条。由于满足Ⅳ类场地条件的记录很少,不具有统计意义,因此,本文未对Ⅳ类场地情况进行研究[1]。限于篇幅,图3仅给出了台湾集集地震中编号为CHY019-N的水平地震记录加速度时程曲线和加速度反应谱曲线。
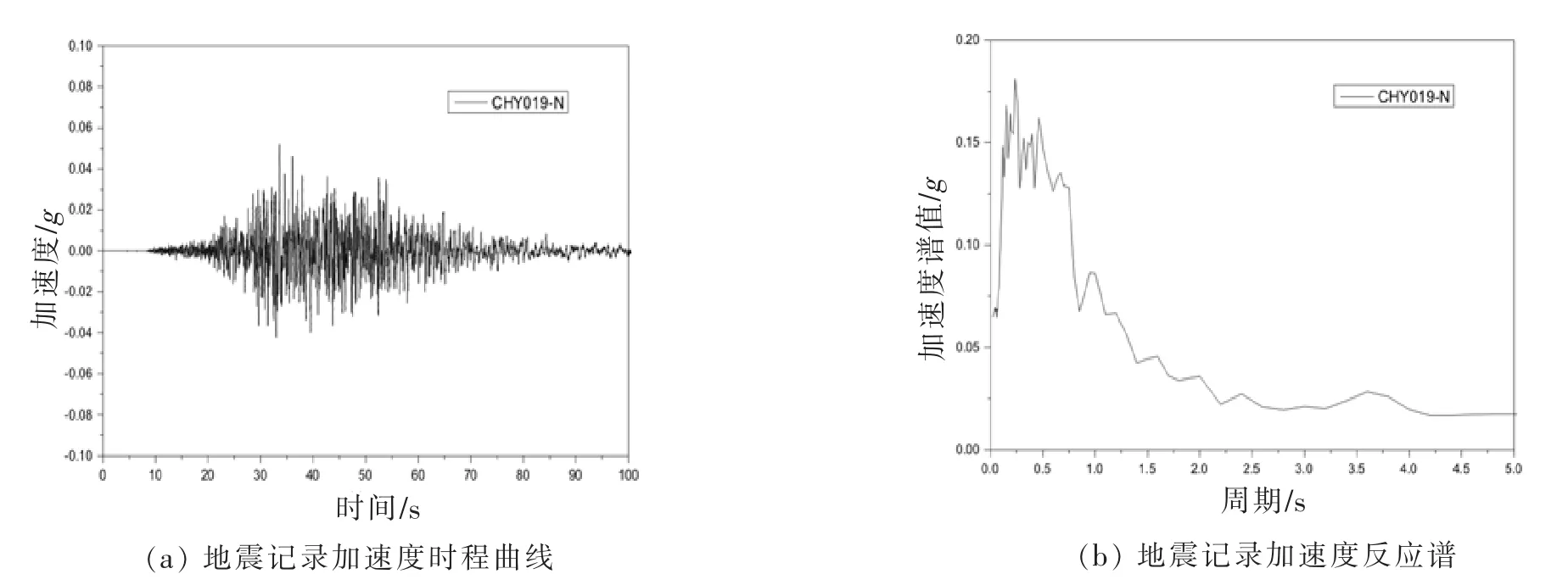
图3 台湾集集地震CHY019-N记录
2.2 增量动力曲线
增量动力分析方法是将地震记录调幅到相同水平的地震动强度,进行时程分析计算结构工程需求参数,然后单调递增地震强度指标进行下一次时程分析,最终得到地震动强度指标与工程需求参数的关系曲线[14]。本文采用基本周期处谱加速度为地震动强度指标进行调幅,从0.2 g以增量0.05 g增加到1 g共调幅17次,然后对结构进行时程分析,若墩顶位移超过结构的极限位移或钢筋断裂即定义为结构倒塌,终止分析。对每座桥梁样本的各工程需求参数,均可得到3类不同场地共47 800条的增量动力曲线。限于篇幅,本文仅绘出地震记录为CHY019-N、编号为3的规则桥梁样本的Park-Ang损伤指标增量动力曲线,如图4所示。
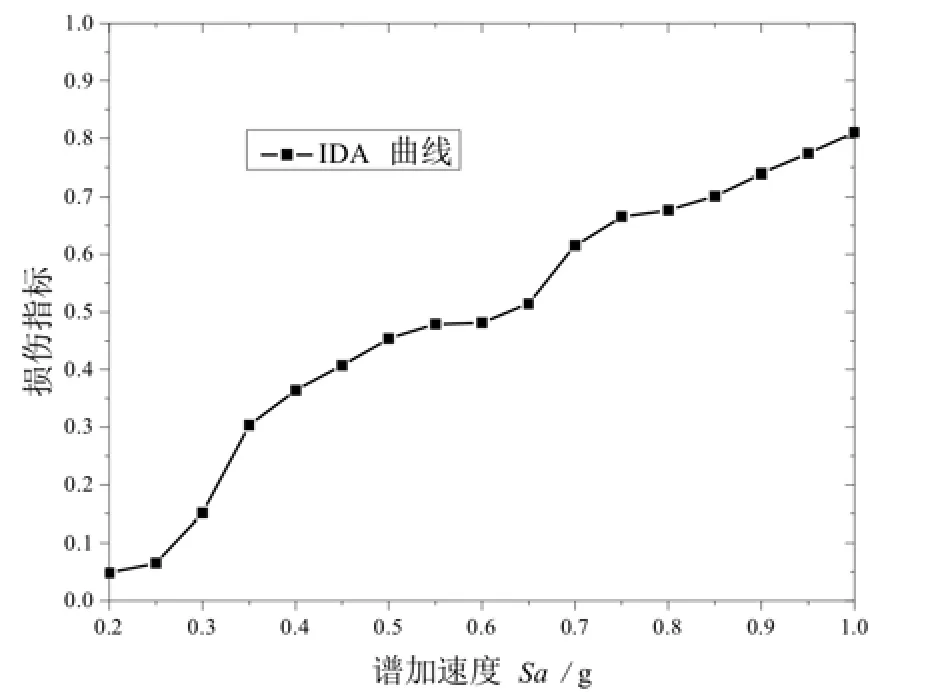
图4 Park-Ang损伤指标增量动力曲线
3 Park-Ang损伤概率需求
P-P图常用于概率分布规律的快速检验。其以样本的累计概率为横轴,以指定理论分布的理论累计概率为纵轴描出散点图,如果待检验样本来自指定理论分布总体,则所有点分布在一条直线附近[15]。图5给出了Ⅱ类场地、编号为3的规则桥梁样本Park-Ang损伤指标正态分布P-P图,从图5可以看出,Park-Ang损伤指标服从正态分布。对各类场地桥梁样本Park-Ang损伤指标进行统计分析,得到正态分布的平均值和标准差。采用回归分析方法,拟合出各类场地的桥梁样本Park-Ang损伤指标平均值简化计算公式1和标准差简化计算公式2。为了检验回归公式1和公式2的计算精度,图6~7分别绘出了采用IDA方法和采用公式计算值的比较,从图6和图7可以直观的看出数据点比较均匀分布在对角线两侧,由此可见,本文所提出的实用公式具有良好的计算精度。

图5 Park-Ang损伤指标正态分布的P-P图
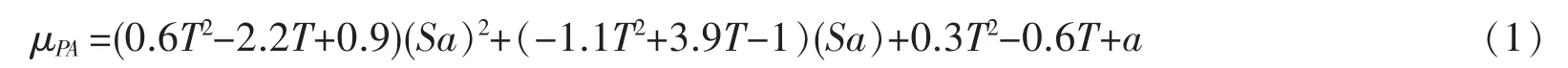
式中a:Ⅰ、Ⅱ类场地取0.1;Ⅲ类场地取0.17。
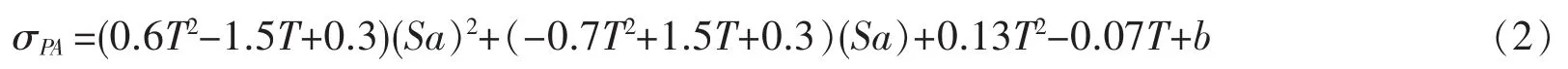
式中b:Ⅰ类场地取-0.13;Ⅱ类场地取-0.1;Ⅲ类场地取-0.09。
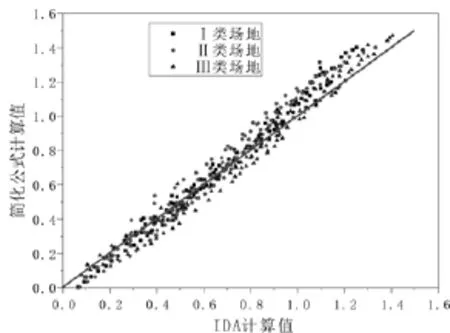
图6 平均值简化公式与IDA计算的比较

图7 标准差简化公式与IDA计算的比较
4 算例分析
某高速公路上一座3跨一联钢筋混凝土规则连续梁桥,桥跨组合为3×30 m,除了在其中的一中墩上设置固定支座外,其余墩(台)均为滑动支座。上部结构采用箱形截面,总重为900 t。下部结构采用圆形截面独柱式桥墩,墩高为10 m,直径为1.5 m。该桥位于Ⅲ类场地,场地特征周期为0.55 s,抗震设防烈度为Ⅷ度。计算该桥在罕遇地震作用下需求危险性。
采用OpenSees软件计算结构基本周期为1 s。根据 《公路桥梁抗震设计细则》(JTG/T B02-01 2008)计算得基本周期处谱加速度为0.386 g。由简化公式1和公式2可以计算出Park-Ang损伤指标平均值为0.46,标准差为0.3。由公式3可以计算得桥梁结构Park-Ang损伤指标需求危险性。从图8可以看出该桥梁结构在1000年一遇的地震作用下Park-Ang损伤指标超过1(即倒塌)的概率为3.6%。


图8 Park-Ang损伤指标危险性曲线
5 结论
(1)选择阻尼比为5%、与结构基本周期对应的谱加速度作为地震动强度指标时,在不同的地震动强度水平下,规则桥梁的Park-Ang损伤指标较好地服从正态分布。
(2)以Park-Ang损伤指标作为工程需求参数,建立了规则桥梁实用的概率地震需求模型;与增量动力分析结果相比,本文所建立的概率地震需求模型具有良好的计算精度。
(3)应用基于Park-Ang损伤指标的规则桥梁概率地震需求模型对一座实例桥进行地震需求危险性分析,计算结果可为决策者基于概率的风险评估提供参考。
[1]曾武华,王逢朝,卓卫东.采用变形和能量双重准则的钢筋混凝土桥墩地震损伤模型[J].华侨大学学报,2016,37(4):441-446.
[2]SEAOC VISION 2000.Performance-based seismic engineering of building[R].Structural Engineering Association of California,1995.
[3]PARK Y J,ANG H S.Mechanistic seismic damage modal for reinforced concrete[J].Journal of Structural Engineering,1985,111(4):722-739.
[4]解咏平,李振宝,杜修力,等.钢筋混凝土柱Park-Ang损伤模型的尺寸效应修正[J].建筑结构,2015(12):13-17.
[5]HAO LIANG,WENY K,FOLIENTE G C.Damage modeling and mamage limit state criterion for wood-frame buildings subjected to seismic loads[J].Journal of Structural Engineering,2011,137(1):41-48.
[6]SIDDHARTHA G,DEBARATI D,KATAKDHOND A A.Estimation of the Park-Ang damage index for planar multi-storey frames using equivalent single-degree systems[J].Engineering Structures,2011,33:2509-2524.
[7]杨伟,欧进萍.基于能量原理的Park&Ang损伤模型简化计算方法[J].地震工程与工程震动,2009,29(2):159-165.
[8]DEBARATI D,SIDDHARTHA G.Uniform hazard spectra based on Park-Ang damage index[J].Journal of Earthquake and Tsunami,2008,2(3):241–258.
[9]涂胡兵,滕军.单自由度体系损伤谱及其应用研究[J].南京理工大学学报,2009,33(6):728-733.
[10]LIU X X,WU Z Y,LIANG F.Multidimensional performance limit state for probabilistic seismic demand analysis[J].Bulletin of Earthquake Engineering,2016,14(12):1-20.
[11]MA H B,ZHUO W D,YIN G,et al.A probabilistic seismic demand model for regular highway bridges[J].Applied Mechanics&Materials,2016,847:307-318.
[12]SHOKRGOZAR H R,ASGARIAN B,GOLSEFIDI E S.Probabilistic seismic evaluation of buckling restrained braced frames using DCFD and PSDA methods[J].Earthquakes&Structures,2016,10(1):1-19.
[13]公路桥梁抗震设计细则:JTG/T B02-01 2008[S].北京:人民交通出版社,2008.
[14]VAMVATSIKOS D,CORNELL C A.Incrementaldynamicanalysis[J].Earthquake Engineering and Structural Dynamics,2004,20(2):491-514.
[15]宗序平,姚玉兰.利用Q-Q图与P-P图快速检验数据的统计分布[J].统计与决策,2010,20:151-152.
(责任编辑:朱联九)
Probability Seismic Demand Analysis for Regular Bridges Based on Park-Ang Damage Index
ZENG Wu-hua1,ZHANG Ren-wei1,WANG Feng-chao1,ZHUO Wei-dong2
(1.School of Civil Engineering,Sanming University,Sanming 365004,China;2.School of Civil Engineering,Fuzhou University,Fuzhou 350116,China)
The probabilistic seismic demand models of regular bridges are derived using the increment dynamic analysis (IDA)method.The demand models are expressed in terms of one intensity measure (IM),i.e.,the spectral acceleration at the fundamental period with 5%damping,and one engineering demand parameter (EDP),i.e.,the Park-Ang damage index.It is found that the EDP is reasonably normal distributed at different IM levels.A correlation between the EDP and the IM are also established using the regression analysis method.At last,the provided models are applied to an example bridge.It reveals that the proposed models can be practically applied to the hazard analysis of seismic demand.
performance-based seismic design(PBSD);regular bridges;probability seismic demand models;increment dynamic analysis(IDA);Park-Ang damage index
U442.55
A
1673-4343(2017)02-0072-06
10.14098/j.cn35-1288/z.2017.02.013
2017-01-12
福建省自然科学基金项目(2016J05132);福建省中青年教师教育科研项目(JAT160465)
曾武华,男,江西金溪人,博士,讲师。主要研究方向:桥梁抗震。
