三次样条插值在通信工程中的应用

2017-05-03索昂代吉

电信科学 2017年1期

关键词：自由空间样条馈线

索昂代吉

（青海省无线电管理办公室玉树管理处，青海玉树 815000）

三次样条插值在通信工程中的应用

索昂代吉

（青海省无线电管理办公室玉树管理处，青海玉树 815000）

在通信工程实践中，经常会遇到离散测量数据的拟合问题，即用已知的有限样本估计一些缺失的未知样本，这时就需要借助插值运算。通过对三次样条插值算法进行研究，将其应用至自由空间损耗计算、馈线插入损耗估计、相关干涉测向3个方面，并通过仿真验证三次样条插值算法在通信工程应用中的有效性。

三次样条插值；自由空间传输损耗；馈线插入损耗；相关干涉测向

1 引言

通信工程实践中，经常遇到离散数据的采样问题，有时因为所涉及的样本较多，会有一部分有用样本未被采集到。一种方法是在采样时尽可能多地将所需样本全部采集到，这种方法得到的数据结果较为准确，但是测量时间较长，导致工作效率降低；另一种方法是用采集到的已知样本来完成一些未知所需样本的计算。而插值作为一种数值逼近的重要方法，可以通过有限个样本的取值情况估计出未知样本的近似值。

目前常见的插值算法有拉格朗日插值、牛顿插值、厄米特插值、样条插值等。前3种插值方式均为线性插值，线性插值计算简单稳定，但是其插值误差较大，而且光滑性较差[1]。因此需要一种更好的插值算法，既有线性插值的优点，又能保证插值精度，使得插值得到的数据和真实数据的误差都在合理范围内，三次样条插值就可以满足上述需求。而且，近年来三次样条插值也已广泛应用至通信领域，参考文献[2]提出将经典对数距离衰减模型中的衰减因子由距离和信号强度的三次样条插值函数代替，在不增加参数的情况下减少模型误差，在指纹识别法校准阶段仅对有限位置的信号强度进行采集，通过衰减模型估计其他位置的信号强度，进而减少校准工作量。参考文献[3]提出将三次样条插值应用于WCDMA移动终端中功率放大器（PA）的校准过程中，通过测量少量采样点配合三次样条插值得到PA的功率曲线。参考文献[4]提出了一种基于三次样条插值的改进去噪算法，利用Ad Hoc算法搜索信号产生模极大值点，形成模极大值线，对于保留下来的模极大值点进行三次样条插值，得到信号的估计小波系数，进而用估计小波系数重构原始信号，达到滤波去噪的目的。除通信领域外，三次样条插值在其他领域也有较广泛的应用，如风洞试验[5]、电力系统信号采样重构[6]等。

2 三次样条插值

数学中的样条（spline）一词来源于它的直观几何背景，绘图员或钣金工人常用弹性木条或金属条加压铁（构成样条）固定在样点上，在其他地方让它自由弯曲，然后画下长条的曲线，称为样条曲线。样条曲线实际上是由分段三次曲线拼接而成，在连接点上要求二阶导数连续，从数学上加以概括就得到数学样条这一概念。

2.1 三次样条插值的函数定义[1]

给定区间[a,b]上的各节点a=x0＜x1＜…＜xn=b和这些节点上的函数值f(xi)=yi(i=0,1,…,n)，若S(x)满足：

·S(xi)=yi(i=0,1,…,n)；

·S(x)在每一个小区间[xi,xi+1](i=0,1,…,n-1)上是次数小于或等于3的多项式；

·S(x)，S′(x)，S″(x)在[a,b]上连续。

则称S(x)为函数f(x)关于节点x0,x1,…,xn的三次样条插值函数。分段三次样条插值曲线如图1所示。

图1 分段三次样条插值曲线

从定义可知，要求出S(x)，在每个小区间[xi,xi+1]上要确定4个待定系数，共有n个小区间，故应确定4n个参数。

根据S(x)在[a,b]上二阶导数连续，在节点xi(i=1,2,…, n-1)处应满足连续性条件：

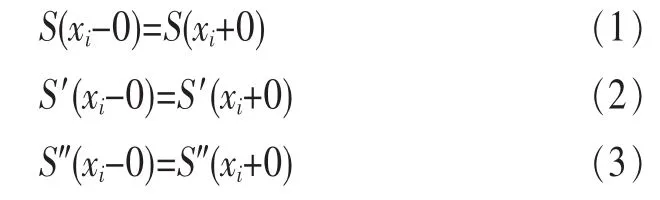
共有3(n-1)=3n-3个条件，再加上S(x)满足插值条件S(xi)=yi(i=0,1,…,n)，总共有3n-3+n+1=4n-2个条件，因此还需要2个条件才能确定S(x)。

通常可在区间[a,b]端点a=x0,b=xn上各加一个条件（称为边界条件），可根据实际问题的要求给定，常见的有以下3种：

·已知两端的一阶导数值，即S′(x0)=f0′，S′(xn)=fn′（固支边界）；

· 已知两端的二阶导数值，即 S″(x0)=f0″，S″(xn)=fn″，（简支边界），特殊情况为S″(x0)=S″(xn)=0（自然边界条件）；

· 当f(x)是以xn-x0为周期的周期函数时，则要求S(x)也是周期函数，这时边界条件应满足：

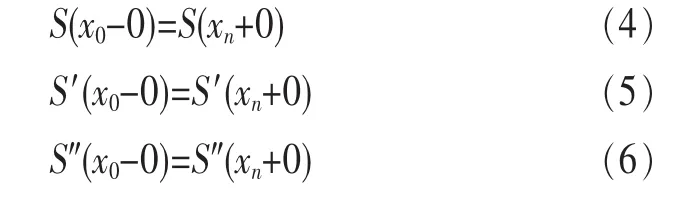
而此时y0=yn，这样确定的样条函数S(x)称为周期样条函数。

2.2 三弯矩算法

三次样条插值函数S(x)可以有多种表达式，有时用二阶导数值S″(x)=Mi(i=0,1,…,n)表示时，使用更为方便。Mi在力学上解释为细梁在xi处的弯矩，并且得到的弯矩与相邻两个弯矩有关，故称用Mi表示S(x)的算法为三弯矩算法。

由于S(x)在区间[xi,xi+1]上是三次多项式，故S′(x)在[xi, xi+1]上是线性函数，可表示为：

对式（7）进行积分，得：

再积分得：

由条件S(xi)=yi、S(xi+1)=yi+1确定积分常数c1、c2：

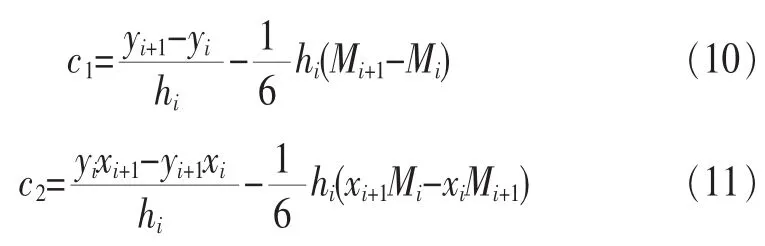
将c1、c2代入三次样条插值函数S(x)的表达式中，可知，只要确定Mi(i=0,1,…,n)这n+1个值，就可定出三次样条插值函数S(x)。

为了确定Mi(i=0,1,…,n)的值，对S(x)求导得：

类似的，对于 x∈[xi-1,xi]：

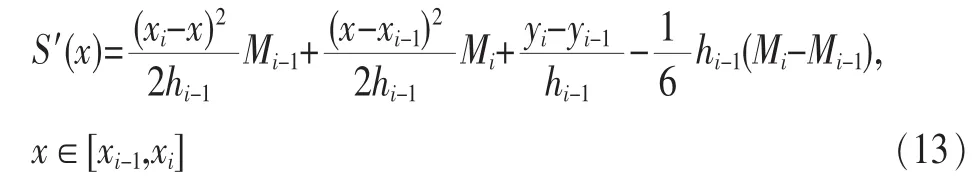
应用导数连续条件S′(xi-0)=S′(xi+0)：

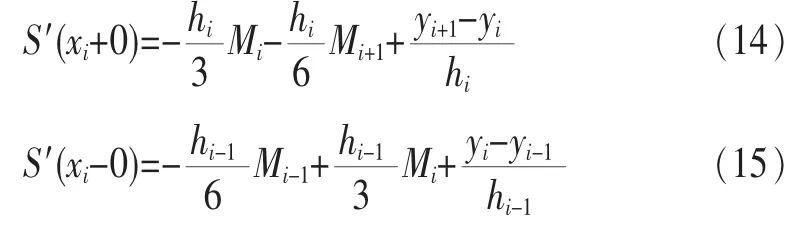
利用 S(x)在内接点的连续性，即 S′(xi-0)=S′(xi+0)可得：

此方程组即三弯矩方程。这是一个含有n+1个未知数、n-1个方程的线性方程，要完全确定Mi(i=0,1,…,n)的值还需要补充两个条件，这两个条件通常根据实际问题的需要，根据插值区间[a,b]两个端点处的边界条件来补充。

（1）已知两端点的一阶导数值S′(x0)=f0′，S′(xn)=fn′

整理式（19）、式（20）得：

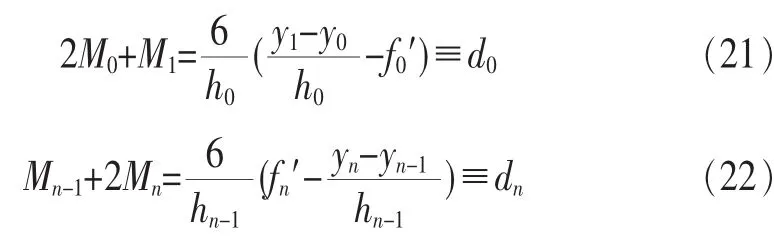
令λ0=1，μn=1，得到Mi(i=0,1,…,n)满足的方程组为：

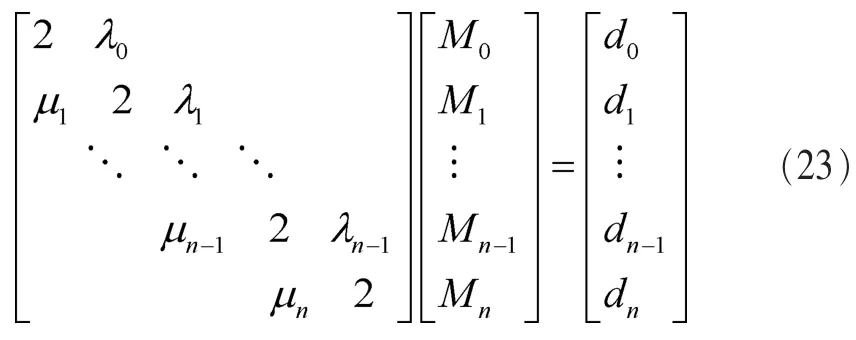
（2）已知两端点的二阶导数值S″(x0)=M0=f0″，S″(xn)=Mn=fn″代入方程（17），只需解n-1个方程，即：

（3）第三类边界条件S′(x0+0)=S′(xn-0)，S″(x0+0)=S″(xn-0)

由式（14）、式（15）及边界条件 S′(x0+0)=S′(xn-0)可得：

又由M0=Mn，三弯矩方程可写为：

式（23）、式（24）、式（28）系数矩阵都是严格对角占优矩阵，因此式（23）、式（24）、式（28）有唯一解，可用追赶法进行求解。

3 三次样条插值在通信工程中的实际应用

选取3个典型实例对三次样条插值在通信工程中的应用来进行验证，并将三次样条插值的结果和线性插值、分段三次厄米特插值算法作对比，以下试验均在国家无线电频谱管理研究所的帮助下完成。

3.1 试验1

在此用自由空间传播损耗[7]作为例子来说明三次样条插值。自由空间传播损耗L0是用在自由空间中两个理想点源天线（增益系数G=1的天线）之间的传播损耗来定义的，它表示在自由空间中，当发射天线与接收天线的增益系数GT=GA=G时，发射天线的输入功率（发射功率）与接收天线的输出功率（接收功率）之比，即：

若以分贝表示：

或：

其中，f为工作频率，d为传播距离。

在试验中，固定f=5 MHz，观察L0随距离d的变化情况，取6个插值点来进行试验，见表1。图2、图3分别给出了不同插值算法的插值结果及误差。

表1 试验中所选取的6个插值点

图2 3种插值算法插值结果

图3 3种不同插值算法的插值误差

从上述结果可以看出，三次样条插值要明显优于线性插值，和分段三次厄米特插值的插值结果不相上下，但是在两个插值点之间斜率较大时，三次样条插值的结果仍要优于分段三次厄米特插值。

3.2 试验2

在实际工作中，经常需要对已有的馈线插入损耗值进行测试，为了减少测试人员的工作量，可以在测试时选取少量的测试点，然后再采用插值的方法获得馈线在未测频点处的插损值。在本次试验中，首先利用标网测量实际在使用的一根金波DC-26.5 GHz低损耗馈线，得到一组原始测试数据，然后从这一组原始数据中选取11个插值点进行插值运算，得到3组不同的插值结果，见表2，其中为选择的11个插值点。3种插值算法的插值误差如图4所示。

从以上结果中可以看出，采用插值方法对馈线插损值进行插值时，在低频段处插值误差较大，高频点处的计算值则可以满足实际需求，因此在使用时，可以将低频点的测试步进选择得尽可能小，高频点处就可以相对选择得稀疏一些。对比3种插值算法，三次样条插值得到的插值结果相对来说误差较小，更适合实际应用。

3.3 试验3

在相关干涉测向中，需要在设计的天线阵列工作频率范围内，按一定规律选择I个均分方位，N个频率建立样本库。在样本库的建立过程中，可以将方位及频率步进尽可能最小化，但是样本采集得越精细，需要耗费的人力以及时间就越多，因此在实际采样时，选择了72个均分方位，即对每一个频点以5°为步进提取原始样本，然后再对实际采样数据进行插值，从而获得每个频点处360°全方位的样本数据。

表2 3种不同插值算法的插值结果

图4 3种插值算法的插值误差

在本次试验中，先采集了360°全方位的样本数据，然后以5°为步进选择插值点，并将插值得到的结果和原始数据进行对比。试验中采用的天线为NSMI-CX0230测向天线，接收机为NSMI-JX03双通道监测测向接收机，该接收机返回的样本为7维的相位差数据，在此选择第一维数据来进行3种插值方法的验证，图5、图6分别给出了3种插值算法的插值结果及误差。

从上述结果中可以看出，3种插值算法得到的结果均可满足实际需求，但在0°～100°方位内，三次样条插值要明显优于另外两种插值算法，证实了三次样条插值算法的有效性。

图5 3种不同插值算法插值结果

图6 3种插值算法插值误差

4 结束语

本文通过对三次样条插值算法进行研究，将其应用至通信工程实践中，并通过MATLAB仿真实现了三次样条插值算法在自由空间损耗计算、馈线插入损耗估计、相关干涉测向3个典型场景下的应用，证实了该插值算法在通信工程应用中的有效性。

[1]孙志忠,吴宏伟,袁慰平,等.计算方法与实习 [M].南京:东南大学出版社,2011. SUN Z Z,WU H W,YUAN W P,et al.An elementary numerical analysls [M].Nanjing:Southeast University Press, 2011.

[2]陈岭,许晓龙,杨清,等.基于三次样条插值的无线信号强度衰减模型[J].浙江大学学报(工学版),2011(9):1521-1527. CHEN L,XU X L,YANG Q,et al.Wireless signal strength propagation model base on cubic spline interpolation[J].Journal of Zhejiang University (Engineering Science),2011(9): 1521-1527.

[3]李迪.三次样条插值在WCDMA移动终端校准中的应用[D].上海:上海交通大学,2009. LI D.Cubic saline interpolation in of WCDMA mobile[D]. Shanghai:Shanghai Jiaotong University,2009.

[4]赵鸿图,刘云.基于三次样条插值的小波模极大值去噪算法[J].计算机工程与设计,2014(8):2965-2968. ZHAO H T,LIU Y.Denoising algorithm of wavelet modulus maximum based on cubic spline interpolation [J].Computer Engineering and Design,2014(8):2965-2968.

[5]杨虎山.三次样条插值在实际问题中的应用和实现[J].忻州师范学院学报,2008,24(2):47-49. YANG H S. The application and realization in a actual problem of cubic spline interpolation[J].Journal of Xinzhou Teachers University,2008,24(2):47-49.

[6]金维刚,刘会金.基于三次样条插值时域采样重构的间谐波检测新算法[J].电网技术,2012,36(7):74-80. JIN W G,LIU H J.A new algorithm for interharmonics measurement based on time domain sampling and reconstruction by cubic spline interpolation [J].Power System Technology, 2012,36(7):74-80.

[7]杨洁,王磊.电磁频谱管理技术 [M].北京:清华大学出版社, 2015. YANG J,WANG L.Electromagnetic spectrum management technology[M].Beijing:Tsinghua University Press,2015.

Application of cubic spline interpolation in communication engineering

SUOANG Daiji
Office of Yushu Radio Management,Wireless Administration of Qinghai Provincial,Yushu 815000,China

In the communication engineering practice,it often needs to estimate the unknown samples which are missing with the limited samples,then the interpolation operation is needed.Based on the research of cubic spline interpolation,the validity was given in communication engineering applications of the cubic spline interpolation by the experimental results on free space loss calculation,feeder insertion loss estimation,correlative interferometer.

cubic spline interpolation,free-space transmission loss,feeder insertion loss,correlation interferometer direction finding

TN99

10.11959/j.issn.1000-0801.2017011